1. Introduction
본 포스트에서는 FAST-LIO2 논문을 리뷰한다. FAST-LIO2는 HKU MaRS 연구실에서 22년도에 발표한 LIO 알고리즘으로 21년도에 발표한 FAST-LIO의 저널 버전이라고 할 수 있다. FAST-LIO2의 가장 큰 특징으로는 ikd-tree를 개발 및 적용하여 kNN 속도를 극적으로 향상시켰으며(kd-tree 대비 4% 시간 소요), 이에 따라 LOAM feature-based에서 Direct point registration 방식으로 LiDAR Odometry 방식이 변경된 것이다.

1.1. FAST-LIO

FAST-LIO의 main contribution은 다음과 같다.
1. Iterated Kalman filter(IKF)를 사용하여 LiDAR와 IMU 센서를 퓨전

2. Backward propagation을 사용하여 포인트클라우드의 왜곡을 보정

3. 효율적인 칼만 게인($\mathbf{K}$)를 사용하여 IEKF의 속도 향상
\begin{equation}
\begin{aligned}
\mathbf{K} = \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal} + \mathbf{R})^{-1} \quad \rightarrow \quad \mathbf{K} = (\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + \mathbf{P}^{-1})^{-1}\mathbf{H}^{\intercal}\mathbf{R}^{-1}
\end{aligned}
\end{equation}
1.2. FAST-LIO2

FAST-LIO2의 main contribution은 다음과 같다.
1. LOAM feature-based에서 Direct point registration 방식으로 Odometry 방식의 변화

2. ikd-tree 기반의 매핑으로 속도 향상 (기존 kd-tree의 4% 연산량만 소요)

FAST-LIO와 FAST-LIO2의 차이점을 알고리즘 파이프라인으로 표현하면 다음과 같다.

2. IMU kinematic model

3차원 공간 상에 위와 같이 IMU가 움직이고 있다고 가정하자. 월드 좌표계는 $\{G\}$이고 IMU 좌표계는 $\{I\}$이다. IMU에 의해 측정되는 가속도는 $\mathbf{a}_m$이다.

측정된(measured) 가속도 $\mathbf{a}_m$은 중력을 포함하고 있다. 따라서 실제(true) IMU가 받고 있는 가속도 $\mathbf{a}_t$는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{a}_t = \mathbf{a}_m - \mathbf{g}
\end{aligned}
\end{equation}

여기에 추가적으로 측정된 IMU 값에는 bias $\mathbf{b}_a$와 센서 자체의 노이즈 $\mathbf{n}_a$이 포함되어 있다. 따라서 $\mathbf{a}_t$를 더 자세히 모델링하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{a}_{t}=\mathbf{a}_{m}-\mathbf{g}-\mathbf{b}_{a}-\mathbf{n}_{a}\end{aligned}
\end{equation}

IMU는 가속도 이외에도 각속도 또한 측정할 수 있다. 측정된 각속도 $\boldsymbol{\omega}_m$ 또한 가속도와 마찬가지로 bias와 노이즈가 존재하게 되고 따라서 다음과 같이 실제 각속도 $\boldsymbol{\omega}_t$를 구할 수 있다.
\begin{equation}
\begin{aligned}
\boldsymbol{\omega}_{t} = \boldsymbol{\omega}_{m} - \mathbf{b}_{w} - \mathbf{n}_{w}
\end{aligned}
\end{equation}

일반적으로 IMU는 LiDAR와 함께 결합된 상태로 3차원 공간 상에서 움직인다. LiDAR와 IMU의 extrinsic은 $^{I}\mathbf{T}_{L} =\ [^{I}\mathbf{R}_{L} \ ^{I}\mathbf{p}_{L}]$와 같이 표기하고 월드 좌표계 $\{G\}$로부터 IMU의 방향, 위치, 속도, bias는 각각 $^{G}\mathbf{R}_{I}, ^{G}\mathbf{p}_{I}, ^{G}\mathbf{v}_{I}, \mathbf{b}_w, \mathbf{b}_a$와 같이 표기한다.
- e.g., $^{G}\mathbf{R}_{I}$ : 월드좌표계 $\{G\}$에서 바라본 IMU 좌표계 $\{I\}$의 방향(orientation)
2.1. State transition model
IMU 시스템을 시간에 따라 업데이트하려면 상태천이모델(state transition model) $\mathbf{f}$를 구해야 한다. $\mathbf{f}$를 구하기 위해서는 IMU의 상태 변수 $\mathbf{x}$의 미분값을 구해야 한다.
우선 IMU의 상태변수 $\mathbf{x}$는 다음과 같이 정의한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{x} \triangleq ( \ ^{G}\mathbf{R}_{I}^{\intercal},\ ^{G}\mathbf{p}_{I}^{\intercal}, \ ^{G}\mathbf{v}_{I}^{\intercal}, \mathbf{b}_{w}^{\intercal}, \mathbf{b}_{a}^{\intercal}, \ ^{G}\mathbf{g}^{\intercal}, \ ^{I}\mathbf{R}_{L}^{\intercal},\ ^{I}\mathbf{p}_{L}^{\intercal})^{\intercal} \in \mathbb{R}^{24}
\end{aligned} }
\end{equation}
- $^{G}\mathbf{R}_{I}$ : 월드좌표계 $\{G\}$에서 바라본 IMU 좌표계 $\{I\}$의 방향(orientation)
- $^{G}\mathbf{p}_{I}$ : 월드 좌표계 $\{G\}$에서 바라본 IMU 좌표계 $\{I\}$의 위치(position)
- $^{G}\mathbf{v}_{I}$ : 월드 좌표계 $\{G\}$에서 바라본 IMU 좌표계 $\{I\}$의 속도(velocity)
- $\mathbf{b}_{w}$ : IMU의 각속도 bias
- $\mathbf{b}_{a}$ : IMU의 가속도 bias
- $^{G}\mathbf{g}$ : 월드 좌표계 $\{G\}$에서 바라본 중력 벡터
- $^{I}\mathbf{R}_{L}$ : IMU 좌표계 $\{I\}$에서 바라본 LiDAR 좌표계 $\{L\}$의 방향(=extrinsic)
- $^{I}\mathbf{p}_{L}$ : IMU 좌표계 $\{I\}$에서 바라본 LiDAR 좌표계 $\{L\}$의 위치(=extrinsic)
색상으로 상태 변수들을 구분하면 다음과 같다.

IMU의 입력 $\mathbf{u}$는 다음과 같이 정의한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{u} \triangleq (\boldsymbol{\omega}_{m}^{\intercal}, \ \mathbf{a}^{\intercal}_m)^{\intercal}
\end{aligned} }
\end{equation}
- $\boldsymbol{\omega}_{m}$ : IMU의 측정 각속도
- $\mathbf{a}_m$ : IMU의 측정 가속도
IMU의 노이즈 $\mathbf{w}$는 다음과 같이 정의한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{w} \triangleq (\mathbf{n}_{w}^{\intercal},\ \mathbf{n}_{a}^{\intercal},\ \mathbf{n}_{bw}^{\intercal},\ \mathbf{n}_{ba}^{\intercal})^{\intercal}
\end{aligned} }
\end{equation}
- $\mathbf{n}_{w}$ : IMU의 각속도 노이즈
- $\mathbf{n}_{a}$ : IMU의 가속도 노이즈
- $\mathbf{n}_{bw}$ : IMU의 각속도 bias 노이즈
- $\mathbf{n}_{ba}$ : IMU의 가속도 bias 노이즈
상태 변수 $\mathbf{x}$의 미분값을 구하면 다음과 같다. 회전행렬 $\mathbf{R}$의 미분은 Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 1의 (77)식을 참조하면 된다.
\begin{equation}
\begin{aligned}
& ^{G}\dot{\mathbf{R}}_{I} =\ ^{G}\mathbf{R}_{I}[{\color{Cyan}\boldsymbol{\omega}_{t}}]_{\times} =\ ^{G}\mathbf{R}_{I}[{\color{Cyan}\boldsymbol{\omega}_{m}-\mathbf{b}_{w} - \mathbf{n}_{w}}]_{\times} \\
& ^{G}\dot{\mathbf{p}}_{I} =\ ^{G}\mathbf{v}_{I} + \frac{1}{2} \int (\ ^{G}\mathbf{R}_{I} {\color{Cyan} \mathbf{a}_t } +\ ^{G}\mathbf{g})dt =\ ^{G}\mathbf{v}_{I} + \frac{1}{2} \int (\ ^{G}\mathbf{R}_{I} {\color{Cyan} (\mathbf{a}_{m}-\mathbf{b}_{a} - \mathbf{n}_{a}) } +\ ^{G}\mathbf{g})dt \\
& ^{G}\dot{\mathbf{v}}_{I} =\ ^{G}\mathbf{R}_{I}{\color{Cyan} \mathbf{a}_{t} }+\ ^{G}\mathbf{g} =\ ^{G}\mathbf{R}_{I} {\color{Cyan}(\mathbf{a}_{m}-\mathbf{b}_{a} - \mathbf{n}_{a}) } +\ ^{G}\mathbf{g} \\
& \dot{\mathbf{b}}_{a} = \mathbf{n}_{ba} \\
& \dot{\mathbf{b}}_{w} = \mathbf{n}_{bw} \\
& ^{G}\dot{\mathbf{g}} = 0 \\
& \dot{^{I}\mathbf{R}_{L}} = \mathbf{0} \\
& ^{I}\dot{\mathbf{p}}_{L} = 0
\end{aligned}
\end{equation}
- $\mathbf{a}_{t}=\mathbf{a}_{m}-\mathbf{b}_{a}-\mathbf{n}_{a}$
- $\boldsymbol{\omega}_{t} = \boldsymbol{\omega}_{m} - \mathbf{b}_{w} - \mathbf{n}_{w}$
따라서 상태천이모델 $\mathbf{f}(\mathbf{x}, \mathbf{u}, \mathbf{w})$는 다음과 같은 24차원 크기의 열벡터가 된다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{f}(\mathbf{x}, \mathbf{u}, \mathbf{w}) = \begin{bmatrix}
\boldsymbol{\omega}_{m}-\mathbf{b}_{w} - \mathbf{n}_{w} \\
^{G}\mathbf{v}_{I} + \frac{1}{2} \int (\ ^{G}\mathbf{R}_{I} (\mathbf{a}_{m}-\mathbf{b}_{a} - \mathbf{n}_{a}) +\ ^{G}\mathbf{g})dt \\
^{G}\mathbf{R}_{I}(\mathbf{a}_{m}-\mathbf{b}_{a} - \mathbf{n}_{a})+\ ^{G}\mathbf{g} \\
\mathbf{n}_{bw}\\
\mathbf{n}_{ba}\\
\mathbf{0}_{3\times 1}\\
\mathbf{0}_{3\times 1}\\
\mathbf{0}_{3\times 1}
\end{bmatrix} \in \mathbb{R}^{24}
\end{aligned} }
\end{equation}
상태천이모델 $\mathbf{f}(\mathbf{x}, \mathbf{u}, \mathbf{w})$을 통해 시간에 따른 IMU 시스템의 변화를 컴퓨터로 연산하기 위해서는 연속 시간(Continuous Time)에 대한 값을 이산 시간(Discrete Time)에 대한 차분 방정식으로 변환해야 한다. 미분 방정식에 대한 수치 해법은 여러 방법(Euler, Mid-point, RK4, etc)들이 있으나 FAST-LIO2는 Euler Method를 사용하였다.
\begin{equation} \label{eq:imukine1}
\boxed{ \begin{aligned}
^{G}\mathbf{R}_{I_{i+1}} &=\ ^{G}\mathbf{R}_{I_i} \boxplus (\boldsymbol{\omega}_{m_i}-\mathbf{b}_{w_i} - \mathbf{n}_{w_i}) \Delta t \\
^{G}\mathbf{p}_{I_{i+1}} &=\ ^{G}\mathbf{p}_{I_i} + \ ^{G}{\mathbf{v}}_{I_i} \Delta t + \frac{1}{2}(\ ^{G}\mathbf{R}_{I} (\mathbf{a}_{m_i}-\mathbf{b}_{a_i} - \mathbf{n}_{a_i}) +\ ^{G}\mathbf{g}_{i}) \Delta t^2 \\
^{G}\mathbf{v}_{I_{i+1}} &=\ ^{G}\mathbf{v}_{I_i} +(\ ^{G}\mathbf{R}_{I} (\mathbf{a}_{m_i}-\mathbf{b}_{a_i} - \mathbf{n}_{a_i}) +\ ^{G}\mathbf{g}_{i}) \Delta t \\
\mathbf{b}_{w_{i+1}} &= \mathbf{b}_{w_i} + {\mathbf{n}}_{bw_i} \Delta t \\
\mathbf{b}_{a_{i+1}} &= \mathbf{b}_{a_i} + {\mathbf{n}}_{ba_i} \Delta t \\
^{G}\mathbf{g}_{i+1} &=\ ^{G}\mathbf{g}_{i} \\
^{I}\mathbf{R}_{L_{i+1}} &=\ ^{I}\mathbf{R}_{L_i} \\
^{I}\mathbf{p}_{L_{i+1}} &=\ ^{I}\mathbf{p}_{L_i} \\
\end{aligned} }
\end{equation}
- $\mathbf{R} \boxplus \mathbf{r}$ : $\mathbf{R} \text{Exp}(\mathbf{r}) \quad \text{where, } \mathbf{R} \in SO(3), \ \mathbf{r} \in \mathbb{R}^{3}$
위 식을 간결하게 표현하면 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{x}_{i+1} = \mathbf{x}_{i} \boxplus (\Delta t f(\mathbf{x}_{i}, \mathbf{u}_{i}, \mathbf{w}_{i}))
\end{aligned} }
\end{equation}
3. LiDAR measurement model

LiDAR 센서에서 $k$번째 스캔의 $j$번째 포인트는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\{\ ^{L}\mathbf{p}_{j}, \ j=1,\cdots,m \ \}
\end{aligned}
\end{equation}
$^{L}\mathbf{p}_{j}$ 값은 LiDAR 센서의 노이즈에 영향을 받는다.
\begin{equation}
\begin{aligned}
^{L}\mathbf{p}_{j}^{\text{gt}} =\ ^{L}\mathbf{p}_{j} + \ ^{L}\mathbf{n}_{j}
\end{aligned}
\end{equation}
- $^{L}\mathbf{n}_{j}$ : $j$번째 포인트에 대한 LiDAR 센서 노이즈
- $^{L}\mathbf{p}_{j}$ : 노이즈가 포함된 $j$번째 포인트
- $^{L}\mathbf{p}_{j}^{\text{gt}}$ : 노이즈가 제거된 실제 $j$번째 포인트의 위치. 위 식에서는 노이즈를 더하는 것으로 제거되었다고 표현하였다.
$^{L}\mathbf{p}_{j}$를 월드 좌표계 $\{G\}$로 변환한다. $^{G}\mathbf{p}_{j} =\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L}\ ^{L}\mathbf{p}_{j}$ 식을 통해 월드 좌표계에서 본 $j$번째 포인트를 $^{G}\mathbf{p}_{j}$라고 하면 $^{G}\mathbf{p}_{j}$와 주변의 다섯 개의 점들 간의 관계는 다음과 같이 정의할 수 있다.

\begin{equation}
\boxed{ \begin{aligned}
0 &=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L}(\ ^{L}\mathbf{p}_{j} +\ ^{L}\mathbf{n}_{j}) -\ ^{G}\mathbf{q}_{j}) \\
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{p}_{j}^{\text{gt}} -\ ^{G}\mathbf{q}_{j}) \\ & = \mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j})
\end{aligned} }
\end{equation}
색상으로 강조하면 다음과 같다.

LiDAR measrement model은 IKF의 업데이트 스텝에 활용되며 이와 같이 관측값 $\mathbf{z}$와 상태 변수 $\mathbf{x}$가 직접적인 매핑 관계 없이 간접적인 조건으로 표현된 경우 이를 implicit measurement model이라고 한다.
4. State estimation
4.1. Backward propagation
LiDAR 센서는 10-100Hz의 속도로 동작하는 것처럼 보이지만 하나 하나의 단일 포인트들은 100-200kHz의 초고속으로 로깅된다. 다만 이렇게 고속으로 데이터를 처리할 수는 없기 때문에 특정 간격(10-100Hz) 동안 데이터를 누적한 다음 한 번에 출력하는데 이를 스캔(scan)이라고 한다.
만약 LiDAR 센서가 움직이면서 포인트를 수집하는 경우 수집된 포인트는 필연적으로 한 스캔에도 여러 포즈가 섞여있을 수 있다. IMU 센서를 활용하면 LiDAR 포인트들을 한 스캔이 끝나는 시점(scan end-time)에 대해 정렬할 수 있으며 이를 Backward propagation이라고 한다.

한 번의 스캔동안 IMU는 forward propagation을 통해 상태를 업데이트 한다. 스캔 속도는 일반적으로 IMU 속도보다 느리기 때문에 한 스캔 사이에도 여러 IMU 측정값들이 존재할 수 있다.

앞서 말했듯이 LiDAR는 한 스캔 내에도 100-200kHz로 로깅된 포인트가 존재하기 때문에 두 IMU 측정값 사이에는 수많은 포인트클라우드 데이터가 존재한다.

- $\hat{\mathbf{x}}_{k}$ : $k$번째 스캔의 상태 변수
- $\hat{\mathbf{P}}_{k}$ : $k$번째 스캔의 공분산
- $\breve{\mathbf{x}}_{j}$ : $j$번째 back-propagation된 포인트
- $^{L_{k}}\mathbf{p}_{j}$ : $k$번째 스캔의 $j$번째 포인트
Backward propagation은 하나의 LiDAR 스캔이 끝나는 순간 IMU 포즈를 역순으로(backward) 전파시켜서 각 IMU 데이터의 포즈를 계산하고 이를 통해 $k$ 시점으로 포인트클라우드의 포즈를 보정하는 방법을 말한다. 이를 통해 모션에 의해 발생하는 포인트들의 왜곡을 보상해줄 수 있다(=motion compensation). 최근으로부터 3개의 IMU 측정값 $j, j-1, j-2$을 자세히 살펴보면 아래와 같다.

한 스캔이 끝나는 순간을 $k$시점이라고 하면 우선 이 때 상태 변수를 $\breve{\mathbf{x}}_{j} = \hat{\mathbf{x}}_k$와 같이 설정한다. 다음으로 시간 역순으로(backward) 상태 변수를 전파하여 $j-1, j-2$ 시점의 상태변수를 구한다.
\begin{equation}
\begin{aligned}
\breve{\mathbf{x}}_{j-1} = \breve{\mathbf{x}}_{j} \boxplus (-\Delta t \mathbf{f}(\breve{\mathbf{x}}_{j}, \mathbf{u}_j, 0))
\end{aligned}
\end{equation}
$j-1, j-2$ 시점의 상태변수를 구하였으면 아래 공식을 통해 $[j-1, j), [j-2, j-1)$ 시간 간격 사이에 있는 LiDAR 포인트들을 전부 $k$시점으로 변환한다.
\begin{equation}
\begin{aligned}
^{L_{k}}\mathbf{p}_{j} =\ ^{I}\mathbf{T}_{L}^{-1}\ ^{I_k}\breve{\mathbf{T}}_{I_j}\ ^{I}\mathbf{T}_{L}\ ^{L_j}\mathbf{p}_{j}
\end{aligned}
\end{equation}
위 과정을 스캔이 시작하는 $k-1$ 시점까지 반복하여 모든 LiDAR 포인트들을 $k$ 시점의 점으로 변환한다.
4.2. Iterated Kalman filter
Iterated Kalman filter(IKF)에 대해 설명하기에 앞서 재귀 베이즈 필터(recursive bayes filter)에 대해 먼저 설명한다. 제어입력 $\mathbf{u}$와 관측값 $\mathbf{z}$가 주어졌을 때 $t$ 시간에서 현재 상태 $\mathbf{x}_{t}$의 믿을만한 정도, 또는 $\mathbf{x}_{t}$에 대한 Belief of $\mathbf{x}_t \ (\text{bel}(\mathbf{x}_{t}))$은 같이 정의한다.
\begin{equation}
\begin{aligned}
\text{bel}(\mathbf{x}_{t}) = p(\mathbf{x}_{t} \ | \ \mathbf{z}_{1:t}, \mathbf{u}_{1:t})
\end{aligned}
\end{equation}
- $\mathbf{x}_{t}$ : t시간에서 상태변수
- $\mathbf{z}_{1:t}$ : 1-t 시간에서 관측값
- $\mathbf{u}_{1:t}$ : 1-t 시간에서 제어입
Belief of $\mathbf{x}_t$를 베이지안 룰에 따라 전개하여 정리하면 다음과 같은 recursive Bayesian filter 수식이 유도된다. 자세한 유도 과정은 칼만 필터(Kalman Filter) 개념 정리 포스팅을 참조하면 된다.
\begin{equation}
\boxed{ \begin{aligned}
& {\color{Cyan} \text{bel}(\mathbf{x}_{t}) } = \eta \cdot p( \mathbf{z}_{t} \ | \ \mathbf{x}_{t}) {\color{Mahogany} \overline{\text{bel}}(\mathbf{x}_{t}) } \\
& {\color{Mahogany} \overline{\text{bel}}(\mathbf{x}_{t}) }= \int p(\mathbf{x}_{t} \ | \ \mathbf{x}_{t-1}, \mathbf{u}_{t}) {\color{Cyan} \text{bel}(\mathbf{x}_{t-1}) } d \mathbf{x}_{t-1}\\
\end{aligned} }
\end{equation}
위 식에서 $\text{bel}(\mathbf{x}_{t})$을 일반적으로 update(또는 correction) 스텝, 그리고 $\overline{\text{bel}}(\mathbf{x}_{t})$을 prediction 스텝이라고 부른다. 만약 $\text{bel}(\mathbf{x}_{t})$, $\overline{\text{bel}}(\mathbf{x}_{t})$가 가우시안 분포를 따르는 경우 이를 특별히 칼만 필터(Kalman filter, KF)라고 부른다.
\begin{equation}
\begin{aligned}
& {\color{Mahogany} \overline{\text{bel}}(\mathbf{x}_{t}) } \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1}) \quad \text{(Kalman Filter Prediction)} \\
& {\color{Cyan} \text{bel}(\mathbf{x}_{t}) } \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t}, \mathbf{P}_{t|t}) \quad \text{(Kalman Filter Update)}
\end{aligned}
\end{equation}
Kalman Filter(KF):
KF는 선형 동적 시스템에 대한 상태의 최적값를 재귀적으로 추정하는 알고리즘을 말한다.

VIO, LIO에서는 일반적으로 빠르게 입력되는 IMU 측정값을 통해 Prediction 스텝을 여러 번 수행하고 카메라, LiDAR 측정값이 들어오면 Update 스텝을 한 차례 수행한다.

3차원 공간 상에서 KF의 prediction, update 스텝을 표현하면 다음과 같다. 아래 그림에서 보다시피 한 스캔 사이에 prediction 스텝은 여러 번 수행된다.

Extended Kalman Filter(EKF):
LIO의 상태변수에는 회전행렬 $\mathbf{R}$이 존재하기 때문에 선형 KF를 사용할 수 없다. 따라서 비선형 상태변수를 선형화(linearzation)로 근사하여 KF를 수행하는 Extended Kalman filter(EKF)를 사용해야 한다.

Iterated Extended Kalman Filter(IEKF):
하지만 EKF는 선형화(linearization) 과정에서 오차가 누적되어 최적해를 보장하지 못하는 단점이 존재한다. IEKF를 사용하면 Update 과정에서 반복적으로(iterated) 선형화를 수행하면서 선형화 에러를 제거하므로 최적해를 보장할 수 있다.

Error-state Kalman Filter(ESKF):
상태 변수 $\mathbf{x}$를 추정하는 EKF와 달리 에러 상태 변수 $\tilde{\mathbf{x}}$를 추정하면 더욱 정확한 추정이 가능하다. 에러 상태 변수를 추정하는 KF를 Error-state Kalman filter(ESKF)라고 한다.

에러 상태 변수를 표현하기 위해 기존의 상태변수는 true 상태 변수가 되고 이는 명목(nominal) 상태 변수와 에러 상태 변수의 합으로 표현한다.
\begin{equation}
\begin{aligned}
\mathbf{x}\ = \ \bar{\mathbf{x}} \ \boxplus \ \tilde{\mathbf{x}}
\end{aligned}
\end{equation}
- $\mathbf{x}$ : true 상태 변수
- $\bar{\mathbf{x}}$ : nominal 상태 변수
- $\tilde{\mathbf{x}}$ : 에러 상태 변수
에러 상태 변수는 값이 작기 때문에 선형화 속도가 빠르고 선형화 누적오차가 작아 정확도가 높은 특성이 있다.
Iterated Error-state Kalman Filter(IESKF):
ESKF의 업데이트 스텝에 iterated Scheme을 추가하면 최종적으로 다음과 같은 형태가 되고 이를 Iterated error-state Kalman filter(IESKF)라고 부른다.
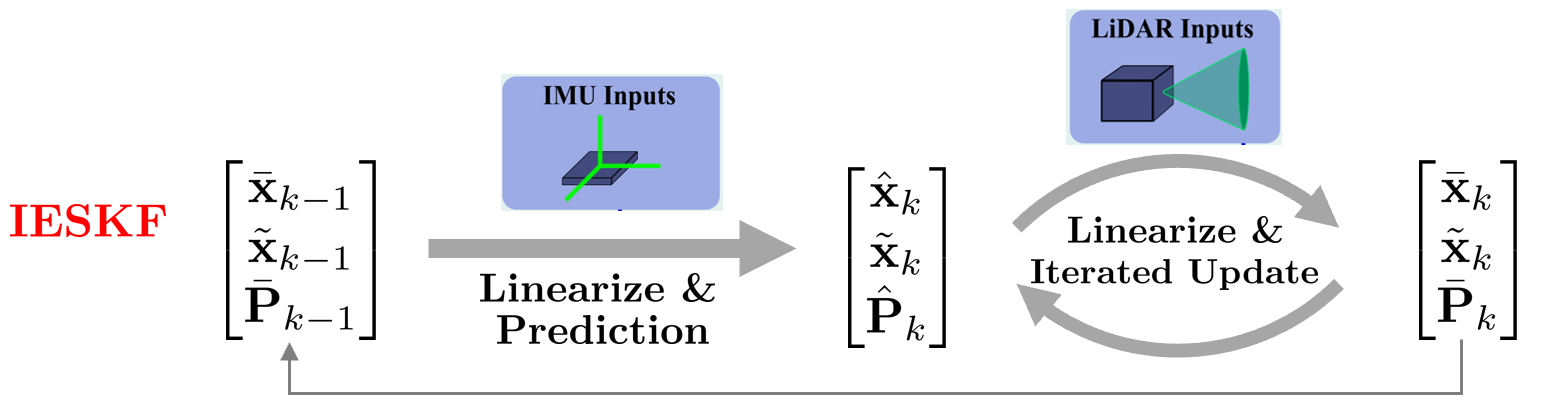
FAST-LIO2에서는 IESKF를 상태 추정에 사용하고 있으며 논문에서는 이를 간략히 Iterated Kalman filter(IKF)라고 표기하였다. IESKF의 모션 모델과 관측 모델은 다음과 같다.
\begin{equation} \label{eq:ikf1}
\begin{aligned}
& \text{Error-state Motion Model: } & \bar{\mathbf{x}}_{k} \boxplus \tilde{\mathbf{x}}_{k} = \mathbf{f}(\bar{\mathbf{x}}_{k-1}, \tilde{\mathbf{x}}_{k-1},\mathbf{u}_{k}, \mathbf{w}_{k}) \\
& \text{Error-state Observation Model: } & \mathbf{z}_{k} = \mathbf{h}(\bar{\mathbf{x}}_{k}, \tilde{\mathbf{x}}_{k}, \mathbf{v}_{k})
\end{aligned}
\end{equation}
- 에러 상태 모션 모델은 $\mathbf{x}_{k} = \mathbf{f}(\mathbf{x}_{k-1}, \mathbf{u}_{k}, \mathbf{w}_{k})$의 에러 상태 버전이다.
- 에러 상태 관측 모델은 $\mathbf{z}_{k} = \mathbf{h}(\mathbf{x}_{k}, \mathbf{v}_{k})$의 에러 상태 버전이다.
Prediction, update 스텝의 자세한 과정을 요약하면 다음과 같다. 이는 다음 섹션에서 자세히 설명한다.

4.2.1. Forward propagation
Forward propagation은 다음 LiDAR 스캔이 들어오기 전까지 IMU 데이터로 prediction 스텝을 수행하는 것을 말한다.

위 그림에서 보는 것과 같이 prediction 스텝은 IMU 데이터가 들어올 때마다 수행되며 상태천이모델 $\mathbf{f}(\hat{\mathbf{x}}_{i}, \hat{\mathbf{u}}_{i}, \mathbf{0}))$를 Euler method를 사용하여 기존 상태 변수 $\mathbf{x}_i$에 더해줌으로써 새로운 상태 변수 $\hat{\mathbf{x}}_{i+1}$를 얻는다. 이전 섹션에서 설명한 (\ref{eq:imukine1})과 동일하다.
\begin{equation} \label{eq:fprop3}
\boxed{ \begin{aligned}
\hat{\mathbf{x}}_{i+1} & = \hat{\mathbf{x}}_{i} \boxplus (\Delta t \mathbf{f}(\hat{\mathbf{x}}_{i}, \hat{\mathbf{u}}_{i}, \mathbf{0})) \\
& = \hat{\mathbf{x}}_{i} \boxplus \Delta t\begin{bmatrix}
\boldsymbol{\omega}_{m_i}-\mathbf{b}_{w_i} - \mathbf{n}_{w_i} \\
^{G}\mathbf{v}_{I_i} + \frac{1}{2}\Big(\ ^{G}\mathbf{R}_{I_i}(\mathbf{a}_{m_i}-\mathbf{b}_{a_i} - \mathbf{n}_{a_i})+\ ^{G}\mathbf{g}_i \Big)\Delta t \\
^{G}\mathbf{R}_{I_i}(\mathbf{a}_{m_i}-\mathbf{b}_{a_i} - \mathbf{n}_{a_i})+\ ^{G}\mathbf{g}_i \\
\mathbf{n}_{bw_i}\\
\mathbf{n}_{ba_i}\\
\mathbf{0}_{3\times 1}\\
\mathbf{0}_{3\times 1}\\
\mathbf{0}_{3\times 1}
\end{bmatrix} \\
& = \begin{bmatrix}
^{G}\mathbf{R}_{I_i} \boxplus (\boldsymbol{\omega}_{m_i}-\mathbf{b}_{w_i} - \mathbf{n}_{w_i})\Delta t \\
^{G}\mathbf{p}_{I_i} + \ ^{G}\mathbf{v}_{I_i}\Delta t + \frac{1}{2}\Big(\ ^{G}\mathbf{R}_{I_i}(\mathbf{a}_{m_i}-\mathbf{b}_{a_i} - \mathbf{n}_{a_i})+\ ^{G}\mathbf{g}_i \Big)\Delta t^2 \\
^{G}\mathbf{v}_{I_i} + (\ ^{G}\mathbf{R}_{I_i}(\mathbf{a}_{m_i}-\mathbf{b}_{a_i} - \mathbf{n}_{a_i})+\ ^{G}\mathbf{g}_i)\Delta t \\
\mathbf{b}_{w_i} + \mathbf{n}_{bw_i}\Delta t \\
\mathbf{b}_{a_i} + \mathbf{n}_{ba_i}\Delta t \\
^{G}\mathbf{g}_{i} \\
^{I}\mathbf{R}_{L_i} \\
^{I}\mathbf{p}_{L_i}
\end{bmatrix}
\end{aligned} }
\end{equation}
- $\mathbf{x} \triangleq ( \ ^{G}\mathbf{R}_{I}^{\intercal},\ ^{G}\mathbf{p}_{I}^{\intercal}, \ ^{G}\mathbf{v}_{I}^{\intercal}, \mathbf{b}_{w}^{\intercal}, \mathbf{b}_{a}^{\intercal}, \ ^{G}\mathbf{g}^{\intercal}, \ ^{I}\mathbf{R}_{L}^{\intercal},\ ^{I}\mathbf{p}_{L}^{\intercal})^{\intercal} \in \mathbb{R}^{24}$
- $\mathbf{R} \boxplus \mathbf{r} : \mathbf{R} \text{Exp}(\mathbf{r}) \quad \text{where, } \mathbf{R} \in SO(3), \ \mathbf{r} \in \mathbb{R}^{3}$
다음으로 에러 상태 $\tilde{\mathbf{x}}$를 구해보자. $\mathbf{x}= \bar{\mathbf{x}} \boxplus \tilde{\mathbf{x}}$(true = nominal + error)이므로 에러 상태 $\tilde{\mathbf{x}}$는 다음과 같이 정의할 수 있다.
\begin{equation} \label{eq:ikf2}
\boxed{ \begin{aligned}
\tilde{\mathbf{x}} = \mathbf{x} \boxminus \bar{\mathbf{x}} = [\delta^{G} \boldsymbol{\theta}_{I}^{\intercal},\ ^{G}\tilde{\mathbf{p}}_{I}^{\intercal}, \ ^{G}\tilde{\mathbf{v}}_{I}^{\intercal}, \tilde{\mathbf{b}}_{w}^{\intercal}, \tilde{\mathbf{b}}_{a}^{\intercal}, \ ^{G}\tilde{\mathbf{g}}^{\intercal},\ \delta^{I} \boldsymbol{\theta}_{L}^{\intercal},\ ^{I}\tilde{\mathbf{p}}_{L}^{\intercal} ]^{\intercal} \in \mathbb{R}^{24}
\end{aligned} }
\end{equation}
- $\delta^{G} \boldsymbol{\theta}_{I} = \text{Log}(\ ^{G}\bar{\mathbf{R}}_{I}^{\intercal} \ ^{G}\mathbf{R}_{I}) \in \mathbb{R}^{3}$ : 월드좌표계에서 바라본 IMU의 회전에 대한 에러 상태 변수
- $\delta^{I} \boldsymbol{\theta}_{L} = \text{Log}(\ ^{I}\bar{\mathbf{R}}_{L}^{\intercal} \ ^{I}\mathbf{R}_{L}) \in \mathbb{R}^{3}$ : IMU 좌표계 바라본 LiDAR 센서의 회전에 대한 에러 상태 변수
에러 상태 모션 모델은 (\ref{eq:ikf1})와 같으므로 이를 선형화하면 다음과 같은 에러 상태에 대한 근사식을 얻을 수 있다. 에러 상태 $\tilde{\mathbf{x}}_{i}$는 이전 스텝에서 리셋되어 항상 $0$의 값을 가지며 노이즈 벡터 $\mathbf{w}$ 또한 평균이 $0$이고 white noise를 가지는 확률변수이므로 해당 값(=operation point)에 대해 테일러 1차 근사를 수행해준다. 자세한 유도 과정은 칼만 필터(Kalman Filter) 개념 정리 포스팅의 식(41)을 참조하면 된다.
\begin{equation}
\begin{aligned}
\bar{\mathbf{x}}_{i+1} \boxplus \tilde{\mathbf{x}}_{i+1} & = \mathbf{f}(\bar{\mathbf{x}}_{i}, \tilde{\mathbf{x}}_{i},\mathbf{u}_{i}, \mathbf{w}_{i}) \\
& \approx \mathbf{f} ( \bar{\mathbf{x}}_{i}, 0,\mathbf{u}_{i}, 0)
+ \mathbf{F}_{\tilde{\mathbf{x}}}(\tilde{\mathbf{x}}_{i}-0)
+ \mathbf{F}_{\mathbf{w}}(\mathbf{w}_{i} -0)
\end{aligned}
\end{equation}
- $\tilde{\mathbf{x}}_{i}=0, \mathbf{w}_{i}=0$ 시점에서 편미분하여 구한 테일러 1차 근사식
위 식에서 $\mathbf{f} ( \bar{\mathbf{x}}_{i}, 0,\mathbf{u}_{i}, 0)$는 정의 상 에러가 없는 nominal 상태 $\bar{\mathbf{x}}_{i+1}$과 동일하므로 서로 소거되어 사라진다. 따라서 아래 식이 유도된다.
\begin{equation} \label{eq:fprop1}
\boxed{ \begin{aligned}
\therefore \tilde{\mathbf{x}}_{i+1} & \approx \mathbf{F}_{\tilde{\mathbf{x}}}\tilde{\mathbf{x}}_{i} + \mathbf{F}_{\mathbf{w}}\mathbf{w}_{i}
\end{aligned} }
\end{equation}
$\mathbf{F}_{\tilde{\mathbf{x}}}, \mathbf{F}_{\mathbf{w}}$는 다음과 같다.
\begin{equation} \label{eq:fprop4}
\begin{aligned}
& \mathbf{F}_{\tilde{\mathbf{x}}} = \begin{bmatrix}
\text{Exp}(-\hat{\boldsymbol{\omega}}_i \Delta t) & \mathbf{0} & \mathbf{0} & {\color{Mahogany} -\mathbf{J}_l(\hat{\boldsymbol{\omega}}_i \Delta t)^{\intercal} } \Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0}& \mathbf{0} \\
\mathbf{0} & \mathbf{I} & \mathbf{I}\Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0}& \mathbf{0}& \mathbf{0} \\
-^{G}\hat{\mathbf{R}}_{I_i}[\hat{\mathbf{a}}_i]_{\times}\Delta t & \mathbf{0} &\mathbf{I} & \mathbf{0} & -^{G}\hat{\mathbf{R}}_{I_i}\Delta t & \mathbf{I}\Delta t& \mathbf{0}& \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} & \mathbf{0} & \mathbf{0}& \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} & \mathbf{0}& \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0}& \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0}
\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}
\end{bmatrix} \in \mathbb{R}^{24\times 24} \\ &
\mathbf{F}_{\mathbf{w}} = \begin{bmatrix}
{\color{Mahogany} -\mathbf{J}_l(\hat{\boldsymbol{\omega}}_i \Delta t)^{\intercal} } \Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & -^{G}\hat{\mathbf{R}}_{I_i}\Delta t & \mathbf{0} & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{I}\Delta t & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}\Delta t \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix} \in \mathbb{R}^{24\times 12}
\end{aligned}
\end{equation}
- $\mathbf{J}_l(\hat{\boldsymbol{\omega}}_i \Delta t)$ : SO(3)군의 왼쪽 자코비안(left jacobian). FAST-LIO2에서는 왼쪽 자코비안 $\mathbf{J}_{l}(\mathbf{u})$을 논문 식(2.5)와 같이 행렬 $\mathbf{A}$로 표현하고 있다. 이에 대한 자세한 설명 및 수식 유도는 Appendix 섹션에서 자세히 다룬다.
각 자코비안 행,열에 상응하는 상태 변수를 나타낸 그림은 다음과 같다.

하지만 에러 상태 $\tilde{\mathbf{x}}_k$는 이전 update 스텝에서 항상 $0$으로 리셋되기 때문에 (\ref{eq:fprop1}) 식은 항상 $0$이 된다. 그렇다면 위와 같이 $\mathbf{F}_{\tilde{\mathbf{x}}_{k}}, \mathbf{F}_{\mathbf{w}}$ 자코비안 행렬을 구하는 이유는 무엇일까? 이는 공분산 $\hat{\mathbf{P}}$를 업데이트하는데 필요하기 때문에 구해야 한다. Prediction 스텝에서 공분산 $\hat{\mathbf{P}}$는 다음과 같이 구할 수 있다.
\begin{equation} \label{eq:fprop2}
\boxed{ \begin{aligned}
\hat{\mathbf{P}}_{i+1} = \mathbf{F}_{\tilde{\mathbf{x}}} \hat{\mathbf{P}}_{i}\mathbf{F}_{\tilde{\mathbf{x}}}^{\intercal} + \mathbf{F}_{\mathbf{w}} \mathbf{Q} \mathbf{F}_{\mathbf{w}}^{\intercal}
\end{aligned} }
\end{equation}
따라서 IKF의 prediction 스텝은 (\ref{eq:fprop3})를 통해 상태 변수 $\hat{\mathbf{x}}$를 구하고 (\ref{eq:fprop2})를 통해 공분산 $\hat{\mathbf{P}}$를 구한다.
4.2.2. Iterated Update
LiDAR 스캔이 들어오면 update 스텝을 수행한다.

IKF는 update 스텝을 반복적(iterative)으로 수행하므로 반복 횟수 $\kappa$를 표기하기 위해 상태 변수를 다음과 같이 변경한다.
\begin{equation}
\begin{aligned}
\hat{\mathbf{x}}_{k}^{\kappa} = \hat{\mathbf{x}}_{k} \quad \quad \text{where } \kappa=0
\end{aligned}
\end{equation}
Residual Computation:
다음으로 측정된 LiDAR 포인트 $^{L}\mathbf{p}_{j}$를 글로벌 좌표계에서 본 포인트 $^{G}\hat{\mathbf{p}}_{j}$로 변환한다.
\begin{equation}
\begin{aligned}
^{G}\hat{\mathbf{p}}_{j}=\ ^{G}\hat{\mathbf{T}}_{I_k}^{\kappa}\ ^{I}\hat{\mathbf{T}}_{L_k}^{\kappa}\ ^{L}\hat{\mathbf{p}}_{j}
\end{aligned}
\end{equation}
그리고 kNN 알고리즘을 사용하여 맵에서부터 $^{G}\hat{\mathbf{p}}_{j}$ 근처 다섯 개의 포인트를 탐색한다. 이 때, ikd-tree로부터 데이터를 가져온다. 다섯 개의 포인트로 평면을 만들고 법선 벡터 $^{G}{\mathbf{u}}_{j}$와 다섯 점의 중심점 $^{G}{\mathbf{q}}_{j}$를 계산한다.

앞서 $^{L}\mathbf{p}_{j}$의 값은 센서 노이즈에 의한 영향을 받는다고 하였다. 이를 고려하여 노이즈가 제거된 값은 $^{L}\mathbf{p}_{j}^{\text{gt}} =\ ^{L}\mathbf{p}_{j} + \ ^{L}\mathbf{n}_{j}$와 같이 나타낼 수 있다. LiDAR measurement model 섹션에서 설명한 것처럼 $^{L}\mathbf{p}_{j}$ 주변의 5개의 맵 포인트와 아래와 같은 관계가 성립한다(=implicit measurement model).
\begin{equation} \label{eq:lidarmeas1}
\boxed{ \begin{aligned}
0 &=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L}(\ ^{L}\mathbf{p}_{j} +\ ^{L}\mathbf{n}_{j}) -\ ^{G}\mathbf{q}_{j}) \\
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{p}_{j}^{\text{gt}} -\ ^{G}\mathbf{q}_{j}) \\ & = \mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j})
\end{aligned} }
\end{equation}
색상으로 강조하면 다음과 같다.


관측 모델을 에러 상태 $\tilde{\mathbf{x}}$에 대해 선형화하면 다음과 같다. 자세한 선형화 과정은 칼만 필터(Kalman Filter) 개념 정리 포스팅의 식(42)을 참조하면 된다.
\begin{equation} \label{eq:iupdate1}
\boxed{ \begin{aligned}
0 & = \mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j}) \\
& \approx \mathbf{h}_{j}(\hat{\mathbf{x}}^{\kappa}_{k},0) +\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa} + \mathbf{v}_j \\
& = \mathbf{z}_{j}^{\kappa} +\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa} + \mathbf{v}_j
\end{aligned} }
\end{equation}
- $\mathbf{z}_{j}^{\kappa} = \mathbf{h}_{j}(\hat{\mathbf{x}}^{\kappa}_{k},0) =\ ^{G}\mathbf{u}_{j}^{\intercal}\Big(\ ^{G}\hat{\mathbf{T}}_{I_k}^{\kappa}\ ^{I}\hat{\mathbf{T}}_{L_k}^{\kappa}\ ^{L}\mathbf{p}_{j} -\ ^{G}\mathbf{q}_{j} \Big)$ : 노이즈가 없을 때(=0) 관측 모델을 의미
- $\mathbf{H}_{j}^{\kappa}$ 행렬에 대한 자세한 수식 유도는 Appendix 섹션에서 다룬다.
Iterated update:
IESKF의 업데이트 스텝은 $\text{bel}(\mathbf{x}_t)$를 확률(probability) 관점이 아닌 최적화(optimization) 관점으로 문제를 해석한다. 업데이트 스텝은 다음과 같이 likelihood와 prior의 식으로 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\bar{\mathbf{x}}_{k} & = \arg\max_{ \mathbf{x}_{k}} \ \text{bel}(\mathbf{x}_{t}) \\
& = \arg\max_{ \mathbf{x}_{k}}\ p(\mathbf{x}_{k} | \mathbf{z}_{1:k}, \mathbf{u}_{1:k}) \quad {\color{black}\cdots \text{posterior}} \\
& \propto \arg\max_{ \mathbf{x}_{k}}\ {\color{Mahogany} p(\mathbf{z}_{k} | \mathbf{x}_{k}) } {\color{Cyan} \overline{\text{bel}}(\mathbf{x}_{k}) } \quad {\color{black} \cdots \text{likelihood} \cdot \text{prior}} \\
& \propto \arg\max_{\mathbf{x}_{k}}\ \exp \bigg( -\frac{1}{2} \bigg[ {\color{Mahogany} \sum_{j=0}^{m} (\mathbf{z}_{j} - \mathbf{h}_j({\mathbf{x}}_k))^{\intercal} \mathbf{R}_{j}^{-1} (\mathbf{z}_{j} - \mathbf{h}_j({\mathbf{x}}_k)) }
+ {\color{Cyan} ( \mathbf{x}_{k} - \hat{\mathbf{x}}_{k})^{\intercal} \hat{\mathbf{P}}_{k}^{-1} ( \mathbf{x}_{k} - \hat{\mathbf{x}}_{k}) } \bigg] \bigg) \\
& \propto \arg\min_{\mathbf{x}_{k}}\ \bigg( {\color{Mahogany} \sum_{j=0}^{m}(\mathbf{z}_{j} - \mathbf{h}_j({\mathbf{x}}_k))^{\intercal} \mathbf{R}_{j}^{-1} (\mathbf{z}_{j} - \mathbf{h}_j({\mathbf{x}}_k)) } + {\color{Cyan} ( \mathbf{x}_{k} - \hat{\mathbf{x}}_{k} )^{\intercal} \hat{\mathbf{P}}^{-1}_{k} ( \mathbf{x}_{k} - \hat{\mathbf{x}}_{k} ) } \bigg)
\end{aligned}
\end{equation}
- $p(\mathbf{z}_{k} | \mathbf{x}_{k}) \sim \mathcal{N}(\mathbf{h}(\mathbf{x}_k), \mathbf{R})$
- $\overline{\text{bel}}(\mathbf{x}_{k}) \sim \mathcal{N}(\hat{\mathbf{x}}_{k}, \hat{\mathbf{P}}_{k})$
위 맨 마지막 식을 정리하면 다음과 같은 최적화 식이 유도된다.
\begin{equation} \label{eq:iupdate2} \boxed{ \begin{aligned}
\bar{\mathbf{x}}_k = \arg\min_{ {\color{Mahogany} {\mathbf{x}}_k } } \quad \sum_{j=0}^{m}\left\| \mathbf{z}_{j} - \mathbf{h}_j({ {\color{Mahogany} \mathbf{x}_k } } ) \right\|^{2}_{\mathbf{R}_j} + \left\| {\color{Mahogany} \mathbf{x}_{k} } - \hat{\mathbf{x}}_{k} \right\|^{2}_{\hat{\mathbf{P}}_{k}}
\end{aligned} }
\end{equation}
- $\mathbf{x}_{k}$ : 최적화해야 하는 true 상태 변수
- $\left\| \mathbf{x} \right\|^{2}_{\mathbf{M}} = \mathbf{x}^{\intercal}\mathbf{M}^{-1}\mathbf{x}$
- $\mathbf{x}_{k} - \hat{\mathbf{x}}_{k}$ : FAST-LIO2에서는 $\mathbf{x}_{k} \boxminus \hat{\mathbf{x}}_{k}$로 표기하였다.
위 식을 에러 상태 변수 $\tilde{\mathbf{x}}$에 대한 수식으로 변경하고 반복적으로 MAP 추정을 하기 위해 ${\kappa}$를 추가해야 한다. 우선 위 식의 왼쪽 부분은 (\ref{eq:iupdate1})을 변형하여 구할 수 있고 오른쪽 부분은 $\mathbf{x}_{k} \boxminus \hat{\mathbf{x}}_{k}$을 에러 상태 변수에 대해 선형화하여 구할 수 있다.
\begin{equation} \label{eq:iupdate3}
\begin{aligned}
0 = \mathbf{z}_{j}^{\kappa} +\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa} + \mathbf{v}_j \quad &\rightarrow \quad \mathbf{z}_{j}^{\kappa} +\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa} = - \mathbf{v}_j \sim \mathcal{N}(0, \mathbf{R}_j) \\
\mathbf{x}_{k} \boxminus \hat{\mathbf{x}}_{k} = (\hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa})\boxminus \hat{\mathbf{x}}_{k} \quad & \overset{\text{linearize}}{\rightarrow} \quad \hat{\mathbf{x}}_{k}^{\kappa} \boxminus \hat{\mathbf{x}}_{k} + \mathbf{J}^{\kappa}\tilde {\mathbf{x}}_{k}^{\kappa} \sim \mathcal{N}(0, \hat{\mathbf{P}}_{k})
\end{aligned}
\end{equation}
위 식에서 $\mathbf{J}^{\kappa}$는 $(\hat{\mathbf{x}}_k^{\kappa} \boxplus \tilde{\mathbf{x}}_k^{\kappa}) \boxminus \hat{\mathbf{x}}_k$를 에러 상태 $\tilde{\mathbf{x}}_k^{\kappa}$에 대해 편미분한 자코비안을 의미한다. (FAST-LIO2 논문 식 (11)의 차원이 이상하다. 잘못 표기된 것으로 보인다.)
\begin{equation} \label{eq:iupdate4}
\begin{aligned}
\mathbf{J}^{\kappa} & = \frac{\partial (\hat{\mathbf{x}}_k^{\kappa} \boxplus \tilde{\mathbf{x}}_k^{\kappa}) \boxminus \hat{\mathbf{x}}_k}{\partial \tilde{\mathbf{x}}_k^{\kappa}} \\ &= \begin{bmatrix}
\mathbf{J}_l(\delta^{G}\boldsymbol{\theta}_{I_k})^{-\intercal} & \mathbf{0}_{3\times 15} & \mathbf{0}_{3\times 3} & \mathbf{0}_{3\times 3} \\
\mathbf{0}_{15\times 3} & \mathbf{I}_{15\times 15} & \mathbf{0}_{15\times 3} & \mathbf{0}_{15\times 3} \\
\mathbf{0}_{3\times 3} & \mathbf{0}_{3\times 15} & \mathbf{J}_l(\delta^{I}\boldsymbol{\theta}_{L_k})^{-\intercal} & \mathbf{0}_{3\times 3} \\
\mathbf{0}_{3\times 3} & \mathbf{0}_{3\times 15} & \mathbf{0}_{3\times 3} & \mathbf{I}_{3\times 3}
\end{bmatrix} \in \mathbb{R}^{24 \times 24}
\end{aligned}
\end{equation}
- $\delta^{G}\boldsymbol{\theta}_{I_k} = \ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa} \boxminus \ ^{G}\hat{\mathbf{R}}_{I_k}$
- $\delta^{I}\boldsymbol{\theta}_{L_k} = \ ^{I}\hat{\mathbf{R}}_{L_k}^{\kappa} \boxminus \ ^{I}\hat{\mathbf{R}}_{L_k}$
$\mathbf{J}^{\kappa}$와 $\mathbf{J}_l$은 표기만 비슷할 뿐 전혀 다른 행렬임에 유의한다. $\mathbf{J}^{\kappa} $는 에러 상태에 대한 자코비안 행렬을 의미하며 $\mathbf{J}_l$은 SO(3)군의 왼쪽 자코비안(left jacobian) 행렬이다.
또한, (\ref{eq:iupdate3}) 아랫 줄 우측 식을 정리하면 에러 상태 변수 $\tilde{\mathbf{x}}_{k}^{\kappa}$의 가우시안 분포를 얻을 수 있다. 이를 통해 공분산 $\mathbf{P}$의 propagation 식을 얻을 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\tilde{\mathbf{x}}_{k}^{\kappa} \sim \mathcal{N}(-(\mathbf{J}^{\kappa})^{-1}(\hat{\mathbf{x}}_{k}^{\kappa} \boxminus \hat{\mathbf{x}}_{k}),\ (\mathbf{J}^{\kappa})^{-1}\hat{\mathbf{P}}_{k}(\mathbf{J}^{\kappa})^{-\intercal})
\end{aligned} }
\end{equation}
- $\mathbf{P} = (\mathbf{J}^{\kappa})^{-1}\hat{\mathbf{P}}_{k}(\mathbf{J}^{\kappa})^{-\intercal}$
따라서 (\ref{eq:iupdate2})의 좌변, 우변을 각각 (\ref{eq:iupdate3})으로 대체하면 다음과 같이 에러 상태 변수에 대한 식으로 변형된다.
\begin{equation} \boxed{ \begin{aligned}
\tilde{\mathbf{x}}_k^{\kappa} = \arg\min_{ {\color{Mahogany} \tilde{\mathbf{x}}_k^{\kappa} } } \quad \sum_{j=0}^{m}\left\| \mathbf{z}_{j}^{\kappa} + \mathbf{H}_j^{\kappa} {\color{Mahogany} \tilde{\mathbf{x}}_{k}^{\kappa} } \right\|^{2}_{\mathbf{R}_j} + \left\| \hat{\mathbf{x}}_{k}^{\kappa} \boxminus \hat{\mathbf{x}}_{k} + \mathbf{J}^{\kappa} {\color{Mahogany} \tilde {\mathbf{x}}_{k}^{\kappa} } \right\|^{2}_{\hat{\mathbf{P}}_{k}}
\end{aligned} }
\end{equation}
- $(\cdot)^{\kappa}$ : iteration 횟수
- $\tilde{\mathbf{x}}_k^{\kappa}$ : 최적화해야 하는 에러 상태 변수
위 식은 quadratic programming(QP) 형태이므로 최적화 식을 풀면 다음과 같은 칼만 필터 업데이트 식이 도출된다. 이를 에러 상태 변수 $\tilde{\mathbf{x}}_{k}^{\kappa}$가 일정 수준 이상 작아질 때까지 반복한다.
\begin{equation}
\boxed{ \begin{aligned}
&\text{while loop} \left\| \tilde{\mathbf{x}}_{k}^{\kappa+1} - \tilde{\mathbf{x}}_{k}^{\kappa} \right\| > \epsilon \\
& \qquad \mathbf{P} = (\mathbf{J}^{\kappa})^{-1}\hat{\mathbf{P}}_{k}(\mathbf{J}^{\kappa})^{-\intercal} \\
& \qquad \mathbf{K} = {\mathbf{P}}\mathbf{H}^{ \intercal}(\mathbf{H}{\mathbf{P}}^{\intercal}\mathbf{H}^{\intercal} + \mathbf{R})^{-1} \\
& \qquad \tilde{\mathbf{x}}_{k}^{\kappa} = (-\mathbf{K}\mathbf{z}_{k}^{\kappa} - (\mathbf{I} - \mathbf{K}\mathbf{H})(\mathbf{J}^{\kappa})^{-1}(\hat{\mathbf{x}}_{k}^{\kappa} \boxminus \hat{\mathbf{x}}_k)) \\
& \qquad \hat{\mathbf{x}}_{k}^{\kappa+1} = \hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa} \\
& \text{end} \\
& \bar{\mathbf{x}}_{k} = \hat{\mathbf{x}}_{k}^{\kappa+1} \qquad \qquad \cdots \text{update state variable} \\
& \bar{\mathbf{P}}_{k} = (\mathbf{I} - \mathbf{K}\mathbf{H}){\mathbf{P}} \qquad \cdots \text{update covariance}
\end{aligned} }
\end{equation}
- $\mathbf{H} = [\mathbf{H}_{1}^{\kappa \intercal}, \cdots, \mathbf{H}_{m}^{\kappa \intercal}]^{\intercal}$
- $\mathbf{R} = \text{diag}(\mathbf{R}_{1}, \cdots, \mathbf{R}_{m})$
그림으로 나타내면 다음과 같다.

하지만 FAST-LIO2는 위 식을 사용하지 않는다. 위 식에서 가장 시간적으로 병목이 되는 부분인 칼만 게인 $\mathbf{K} = \mathbf{P}\mathbf{H}^{ \intercal}(\mathbf{H}{\mathbf{P}}^{\intercal}\mathbf{H}^{\intercal} + \mathbf{R})^{-1}$를 구하는 부분을 동치(equivalent) 관계의 칼만 게인 $\mathbf{K} = (\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + {\mathbf{P}}^{-1})^{-1}\mathbf{H}^{\intercal}\mathbf{R}^{-1}$으로 변경하여 연산 속도를 대폭 감소시켰다.
4.2.3. Fast Kalman gain
FAST-LIO2에서는 동치(equivalent) 관계의 다른 칼만 게인을 구하여 연산 속도를 대폭 감소시켰다.
\begin{equation}
\begin{aligned}
\mathbf{K} = {\mathbf{P}}\mathbf{H}^{ \intercal}({\color{Mahogany} \mathbf{H}{\mathbf{P}}^{\intercal}\mathbf{H}^{\intercal} + \mathbf{R} } )^{-1} \quad &\rightarrow \quad \mathbf{K} = ( {\color{Cyan} \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + {\mathbf{P}}^{-1} } )^{-1}\mathbf{H}^{\intercal}\mathbf{R}^{-1}
\end{aligned}
\end{equation}
LiDAR 스캔 당 1-100k의 관측 데이터가 생성되기 때문에 역행렬 $(\mathbf{H}\mathbf{P}\mathbf{H}^{\intercal}+\mathbf{R})^{-1}$을 구하는데 많은 시간이 소요된다. 우선 $\mathbf{H} = [\mathbf{H}_{1}^{\kappa \intercal}, \cdots, \mathbf{H}_{m}^{\kappa \intercal}]^{\intercal}$ 행렬에 대해 자세히 살펴보자. 앞서 LiDAR measurement model (\ref{eq:lidarmeas1})에서 $j$번째 포인트에 대한 $\mathbf{H}_{j}^{\kappa}$는 다음과 같이 유도되었다.
\begin{equation}
\begin{aligned}
0 &=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L}(\ ^{L}\mathbf{p}_{j} +\ ^{L}\mathbf{n}_{j}) -\ ^{G}\mathbf{q}_{j}) \\
& = \mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j}) \\
& \approx \mathbf{h}_{j}(\hat{\mathbf{x}}_k^{\kappa}, 0) +{\color{Mahogany} \mathbf{H}_{j}^{\kappa} }\tilde{\mathbf{x}}_{k}^{\kappa} + \mathbf{v}_j
\end{aligned}
\end{equation}

(\ref{eq:ikf2})에서 에러 상태 변수 $\tilde{\mathbf{x}}$는 24차원의 상태를 갖고 있기 때문에 $\mathbf{H}_{j}^{\kappa}$는 $1\times 24$의 크기를 가진다.
\begin{equation}
\begin{aligned}
& \tilde{\mathbf{x}} = \mathbf{x} \boxminus \bar{\mathbf{x}} = [\delta \boldsymbol{\theta},\ ^{G}\tilde{\mathbf{p}}_{I}^{\intercal}, \ ^{G}\tilde{\mathbf{v}}_{I}^{\intercal}, \tilde{\mathbf{b}}_{w}^{\intercal}, \tilde{\mathbf{b}}_{a}^{\intercal}, \ ^{G}\tilde{\mathbf{g}}^{\intercal}, \ \delta \boldsymbol{\theta}^{'\intercal},\ ^{I}\tilde{\mathbf{p}}_{L}^{\intercal} ]^{\intercal} \in \mathbb{R}^{24} \\
&\mathbf{H}_{j}^{\kappa} \in \mathbb{R}^{1\times 24}
\end{aligned}
\end{equation}

칼만 게인을 동치(equivalent) 관계의 다른 형태로 변환하면 $m\times m$의 역행렬을 구하지 않고 $24\times 24$ 크기의 역행렬만 구하면 된다.
\begin{equation}
\begin{aligned}
\mathbf{K} = {\mathbf{P}}\mathbf{H}^{ \intercal}({\color{Mahogany} \mathbf{H}{\mathbf{P}}^{\intercal}\mathbf{H}^{\intercal} + \mathbf{R} } )^{-1} \in \mathbb{R}^{24\times m} \quad &\rightarrow \quad \mathbf{K} = ( {\color{Cyan} \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + {\mathbf{P}}^{-1} } )^{-1}\mathbf{H}^{\intercal}\mathbf{R}^{-1} \in \mathbb{R}^{24\times m}
\end{aligned}
\end{equation}

역행렬은 대략 $O(n^{3})$ 정도의 시간복잡도가 요구되기 때문에 $m$이 240개만 넘어가도 Fast 칼만 게인보다 Slow 칼만 게인이 100배 넘게 느린 것을 알 수 있다. 일반적인 LiDAR 스캔에서 포인트클라우드는 대략 $m \approx 1-100k$이기 때문에 Slow 칼만게인은 실시간 성능이 보장되지 않음을 알 수 있다. 반면에 Fast 칼만 게인은 $24\times 24$로 크기가 고정이기 때문에 포인트의 개수에 관계없이 속도가 일정하다.
Derivation of Fast Kalman gain:
두 칼만 게인이 동치 관계인 것을 증명해보자. FAST-LIO 논문에서는 Fast -> Slow 순서로 증명하였다. 우선 $( {\color{Cyan} \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + {\mathbf{P}}^{-1} } )^{-1}$에 matrix inversion lemma를 사용하면 식을 다음과 같이 변경할 수 있다.
\begin{equation}
\begin{aligned}
( {\color{Cyan} {\mathbf{P}}^{-1} + \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} } )^{-1} = \mathbf{P} - \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal}+\mathbf{R})^{-1}\mathbf{HP}
\end{aligned}
\end{equation}
위 식을 Fast 칼만 게인에 넣고 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{K} & = ({\color{Cyan} \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + {\mathbf{P}}^{-1} } )^{-1}\mathbf{H}^{\intercal}\mathbf{R}^{-1} \\
& =\Big(\mathbf{P} - \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal}+\mathbf{R})^{-1}\mathbf{HP}\Big)\mathbf{H}^{\intercal}\mathbf{R}^{-1} \\
& = \mathbf{PH}^{\intercal}\mathbf{R}^{-1} - \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal} + \mathbf{R})^{-1} \mathbf{HPH}^{\intercal}\mathbf{R}^{-1}
\end{aligned}
\end{equation}
$\mathbf{HPH}^{\intercal}\mathbf{R}^{-1} = (\mathbf{HPH}^{\intercal}+\mathbf{R})\mathbf{R}^{-1} - \mathbf{I}$이므로 이를 위 식에 넣어주면 Slow 칼만 게인이 도출된다.
\begin{equation}
\begin{aligned}
\mathbf{K} & = \mathbf{PH}^{\intercal}\mathbf{R}^{-1} - \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal} + \mathbf{R})^{-1} \Big( (\mathbf{HPH}^{\intercal}+\mathbf{R})\mathbf{R}^{-1} - \mathbf{I} \Big) \\
& = \mathbf{PH}^{\intercal}\mathbf{R}^{-1} - \mathbf{PH}^{\intercal}\mathbf{R}^{-1} + \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal} + \mathbf{R})^{-1} \\
& = \mathbf{PH}^{\intercal}({\color{Mahogany} \mathbf{HPH}^{\intercal} + \mathbf{R} } )^{-1}
\end{aligned}
\end{equation}
색상으로 강조하면 다음과 같다.

결론적으로 FAST-LIO2는 다음 식을 반복적으로 계산하면서 업데이트 과정을 수행한다.
\begin{equation}
\boxed{ \begin{aligned}
&\text{while loop} \left\| \tilde{\mathbf{x}}_{k}^{\kappa+1} - \tilde{\mathbf{x}}_{k}^{\kappa} \right\| > \epsilon \\
& \qquad \mathbf{P} = (\mathbf{J}^{\kappa})^{-1}\hat{\mathbf{P}}_{k}(\mathbf{J}^{\kappa})^{-\intercal} \\
& \qquad \mathbf{K} = ({\color{Cyan}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + {\mathbf{P}}^{-1} } )^{-1}\mathbf{H}^{\intercal}\mathbf{R}^{-1} \\
& \qquad \tilde{\mathbf{x}}_{k}^{\kappa} = (-\mathbf{K}\mathbf{z}_{k}^{\kappa} - (\mathbf{I} - \mathbf{K}\mathbf{H})(\mathbf{J}^{\kappa})^{-1}(\hat{\mathbf{x}}_{k}^{\kappa} \boxminus \hat{\mathbf{x}}_k)) \\
& \qquad \hat{\mathbf{x}}_{k}^{\kappa+1} = \hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa} \\
& \text{end} \\
& \bar{\mathbf{x}}_{k} = \hat{\mathbf{x}}_{k}^{\kappa+1} \qquad \qquad \cdots \text{update state variable} \\
& \bar{\mathbf{P}}_{k} = (\mathbf{I} - \mathbf{K}\mathbf{H}){\mathbf{P}} \qquad \cdots \text{update covariance}
\end{aligned} }
\end{equation}
- $\mathbf{H} = [\mathbf{H}_{1}^{\kappa \intercal}, \cdots, \mathbf{H}_{m}^{\kappa \intercal}]^{\intercal}$
- $\mathbf{R} = \text{diag}(\mathbf{R}_{1}, \cdots, \mathbf{R}_{m})$
그림으로 나타내면 다음과 같다.

5. Mapping - ikd-tree

IKF 업데이트 스텝이 끝나면 $m$개의 LiDAR 포인트는 글로벌 좌표계로 변환된다.
\begin{equation}
\begin{aligned}
^{G}\bar{\mathbf{p}}_{j} =\, ^{G}\bar{\mathbf{T}}_{I_k}\, ^{I}\bar{\mathbf{T}}_{L_k}\, ^{L}{\mathbf{p}}_{j} \qquad j=1,\cdots,m
\end{aligned}
\end{equation}
기존 FAST-LIO는 kNN 탐색을 위해 $^{G}\bar{\mathbf{p}}_{j}$를 kd-tree에 저장하였으나 맵(=트리)의 크기가 커질수록 삽입/삭제/탐색에 소요되는 시간이 점진적으로 증가하는 단점이 존재한다.
- 정적 kd-tree는 포인트를 삽입/삭제될 때 자동으로 리밸런싱이 되지 않으므로 시간이 지남에 따라 불균형이 심해진다.
- 수동 리밸런싱을 하게 되면 전체 트리를 리밸런싱해야 하므로 연산량이 많이 소요된다.
LIO와 같은 로봇 어플리케이션은 실시간으로 데이터의 삽입/삭제가 빈번하게 일어나므로 대규모 매핑 시 kd-tree로는 실시간 성능을 보장할 수 없다.

FAST-LIO2는 데이터 변경 시 자동으로 부분 트리만 리밸런싱하는 동적 icremental kd-tree(ikd-tree)를 개발 및 적용하였다. ikd-tree는 모든 테스트에서 kd-tree의 4%의 시간만 소비하였다.
5.1. kd-tree
kd-tree는 1975년 존 벤틀리에 의해 제안된 자료구조로서 $k$차원 공간에서 데이터를 효율적으로 구성하고 검색하기 위한 자료구조이다. 이진검색트리(binary search tree)를 다차원으로 확장한 형태로 각 노드는 $k$차원 점을 의미하며 각 분할 단계에서 하나의 차원을 선택하여 그 차원에 대한 값으로 노드를 분할한다. 포인트클라우드 같은 큰 데이터를 효율적으로 삽입/삭제/탐색할 수 있어서 LiDAR 데이터를 다룰 때 광범위하게 사용되며 일반적으로 kNN 알고리즘에서 주변의 점들을 빠르게 탐색하기 위한 자료구조로 kd-tree를 사용한다.

예를 들어 위 그림에서 검정색 포인트들은 이미 주어져 있고 새로운 파란색 포인트가 들어왔을 때 최단 거리를 찾는다고 가정해보자(=kNN). 왼쪽 그림에서는 최단 거리를 찾기 위해 모든 점들에 대해 거리를 계산해야 하지만 오른쪽 그림은 kd-tree에 의해 공간이 효율적으로 분할되어 있기 때문에 분할된 공간 내에서 파란색 포인트와 가장 가까운 점들 몇 개만 탐색하면 최소 거리를 구할 수 있다. 따라서 $O(n)$이 걸리는 최소 거리 찾기 문제를 kd-tree를 사용하면 평균적으로 $O(\log n)$에 해결할 수 있게 된다.
5.1.1. Point insertion
2차원 $(k=2)$ 데이터를 삽입하는 예제를 살펴보자.

오른쪽 2차원 그래프에 점들이 주어져 있을 때 이를 kd-tree에 삽입하는 연산에 대해 먼저 알아보자.

맨 처음 축(axis)을 $x$축으로 설정하고 데이터를 $x$축 기준으로 정렬한다. 그리고 중앙값(median)을 선택한다. 예제에서는 데이터가 짝수인 경우 뒷쪽의 중앙값을 선택하였다. 따라서 $(7,2)$가 루트 노드(root node)가 된다. $(7,2)$에 의해 그래프는 $x$축으로 분할되고 왼쪽에는 $(2,3), (5,4), (4,7)$가 존재하며 오른쪽에는 $(8,1), (9,6)$이 존재한다.

다음으로 $y$축을 선택한다. 분할된 영역마다 $y$축을 기준으로 데이터를 정렬하고 중앙값을 선택한다. 이전 노드보다 $x$값이 작은 $(5,4)$는 왼쪽 자식(left child) 노드에 위치하고 $x$값이 큰 $(9,6)$는 오른쪽 자식(right child) 노드에 위치한다.

$y$축으로 분할된 후 남은 원소가 각각 하나씩이므로 전부 말단 노드(leaf node)로 설정한다. 이전 노드보다 $y$값이 작은 $(2,3), (8,1)$는 왼쪽 자식 노드에 위치하고 $y$값이 큰 $(4,7)$는 오른쪽 자식 노드에 위치한다.
5.1.2. kNN search
다음으로 kd-tree에서 kNN을 수행하는 예제를 살펴보자. $(2,5)$ 포인트가 주어졌을 떄 이와 가장 가까운 점을 구해야 한다. 전체 알고리즘은 다음과 같다.
- 루트 노드로부터 재귀적으로(recursive) 데이터 삽입과 동일한 액션을 수행하여 말단 노드(leaf node)까지 이동
- 말단 노드와 타겟포인트 사이의 거리를 closest dist.에 저장
- 지나온 노드들을 거슬러 올라가면서 아래 과정을 수행
- 3.1. 현재 노드와 거리를 측정하고 closest dist.보다 더 가깝다면 업데이트
- 3.2. 분할된 평면 반대편을 다음 과정을 통해 체크. 분할된 평면까지 거리와 closest dist.를 비교
- 3.2.1. closest dist.가 큰 경우 반대 영역의 브랜치도 탐색
- 3.2.2. closest dist.가 작은 경우 반대 브랜치는 고려하지 않고 3번 과정을 반복
- 루트 노드까지 과정을 반복 후 탐색 종료

타겟 포인트 $(2,5)$가 주어졌고 이와 가장 가까운 포인트를 찾아야 한다.

1. 루트 노드로부터 재귀적으로(recursive) 데이터 삽입과 동일한 액션을 수행하여 말단 노드(leaf node)까지 이동

2. 말단 노드와 타겟포인트 사이의 거리를 closest dist.에 저장

(3) 3.2. 분할된 평면 반대편을 다음 과정을 통해 체크. 분할된 평면까지 거리와 closest dist.를 비교

(3) 3.2.1. closest dist.가 큰 경우 반대 영역의 브랜치도 탐색

(3) 3.1. 현재 노드와 거리를 측정하고 closest dist.보다 더 가깝다면 업데이트

(3) 3.2. 분할된 평면 반대편을 다음 과정을 통해 체크. 분할된 평면까지 거리와 closest dist.를 비교


4. 루트 노드까지 과정을 반복 후 탐색 종료
5.2. ikd-tree

kd-tree는 정적 자료구조이므로 자동으로 리밸런싱을 수행하지 않는다. 따라서 시간이 지날수록 트리가 불균형해지는 문제 발생한다. 불균형 문제를 해결하기 위해 Scapegoat tree, Balanced Box-decomposition(BBD) tree, Incremental kd-tree(ikd-tree) 등 동적으로 밸런싱을 수행하는 kd-tree 알고리즘들이 제안되었다. 이 중 ikd-tree는 점진적으로(incrementally) 데이터가 추가/삭제될 때마다 부분 트리를 동적으로 업데이트하는 특징이 있다.
5.2.1. Balancing criterion
ikd-tree는 아래 조건이 만족되면 트리의 밸런스가 맞춰졌다고 판단한다. 즉, 아래 조건 중 하나라도 위반되면 동적으로 리밸런싱을 수행한다.
\begin{equation}
\boxed{ \begin{aligned}
S(T.leftchild) & < \alpha_{bal}\Big( S(T) -1 \Big) \\
S(T.rightchild) & < \alpha_{bal}\Big( S(T) -1 \Big) \\
I(T) & < \alpha_{del}S(T)
\end{aligned} }
\end{equation}
- $\alpha_{bal} \in (0.5, 1)$
- $\alpha_{del} \in (0, 1)$
- $S(T)$ : $T$가 루트 노드인 트리에서 노드의 전체 개수
- $I(T)$ : $T$가 루트 노드인 트리에서 삭제 마킹(invalidnum)된 포인트의 개수
위 첫 두 줄의 식을 통해 루트 노드가 $T$일 때 왼쪽 자식과 오른쪽 자식 노드의 개수를 관리하며 마지막 줄의 식을 통해 삭제로 마킹된 invalidnum의 개수가 일정 개수 이상 넘어가게 되면 리밸런싱을 수행한다.

위 왼쪽 그림에서 오른쪽 자식 노드는 $9$개인 반면 조건은 $6.5$이므로 조건이 위배되어 해당 트리는 리밸런싱을 수행한다. 마찬가지로 위 오른쪽 그림에서 invalidnum 처리된 포인트는 $4$개인 반면 조건은 $2.8$이므로 해당 트리는 리밸런싱을 수행한다.
5.2.2. Map management

ikd-tree가 맵을 관리하는 방법은 다음과 같다.
- 초기 맵 크기 $L$(e.g., 1000m)만큼 ikd-tree를 유지함. 초기 LiDAR 포즈는 $\mathbf{p}_0$이며 $\mathbf{r}$ 크기 만큼 탐지 가능
- 시간이 지남에 따라 LiDAR 센서가 이동하여 $\mathbf{p}'$로 이동하고 맵의 경계 부분을 터치함
- 전체 맵은 $\mathbf{d}$만큼 이동하고 이전의 겹치지 않는 부분들은 전부 삭제됨 (=Box-wise 삭제 발생)
5.2.3. Advantages

ikd-tree는 다음과 같은 장점을 지닌다.
- 증분 업데이트와 리밸런싱 : 단일 포인트의 삽입/삭제 외에도 박스 단위의(box-wise) 삽입/제거 연산도 지원하며 동적으로 리밸런싱을 수행함
- 다운샘플링 지원 : 트리 구조 내에서 자체적으로 다운샘플링 기능을 지원함. 이를 통해 맵데이터를 효율적으로 관리하면서 필요한 정밀도를 유지할 수 있게 됨
- 레이지 삭제(lazy deletion) : 삭제 연산 수행 시 실제 점들이 삭제되지 않고 삭제됨으로 마킹해놓은 다음 리밸런싱 시 실제로 삭제됨. 이는 삭제 과정의 효율성을 크게 향상시키며 리밸런싱 시간을 절약할 수 있음
- 병렬 리밸런싱 기능 : 큰 서브 트리의 리밸런싱이 필요한 경우 병렬 처리를 사용하여 성능 저하없이 빠르게 리밸런싱 가능
ikd-tree와 kd-tree의 시간복잡도를 비교하면 다음과 같다.

ikd-tree와 다른 kd-tree 알고리즘들의 기능을 비교하면 다음과 같다.

5.2.4. Data structure
ikd-tree의 자료구조는 다음과 같다.

5.2.5. Algorithm detail
Point insertion / Downsampling:

Box-delete:

Rebalancing:

6. Experiments
6.1. Benchmark experiment

FAST-LIO2의 성능 평가를 위해 위와 같은 공개 벤치마크 데이터셋을 사용하였다.
6.1.1. ikd-tree speed test
각 벤치마크 데이터셋에서 ikd-tree와 다른 트리 자료구조의 속도를 평가

6.1.2. FAST-LIO2 performance test

6.2. Real-world experiment

벤치마크 테스트에서 다른 알고리즘 대비 좋은 결과를 얻은 후 자체적으로 드론에 LiDAR+IMU을 부착하여 테스트를 수행하였다.
6.2.1. FAST-LIO2 processing time test

6.2.2. FAST-LIO v.s. FAST-LIO2 processing time

6.2.3. Fast flip test
1000deg/s의 매우 빠른 회전 테스트

6.2.4. Fast movement test
7m/s, 100deg/s 속도로 달리면서 테스트

6.2.5. Aerial drone test
드론의 바닥면에 LiDAR를 설치하여 공중에서 FAST-LIO2를 수행

7. Appendix
해당 섹션에서는 FAST-LIO2 논문의 내용 중 설명의 편의를 위해 수식적으로 깊게 다루지 못했던 부분을 다룬다. 주로 R2Live 논문과 IMU preinegration 논문을 참고하여 작성하였다[5][6].
7.1. Left and right jacobian of SO(3)
임의의 회전행렬 $\mathbf{R} \in SO(3)$가 주어졌을 때 이를 지수 매핑(exponential mapping)에 대한 식으로 표현하면 다음과 같다. 보다 자세한 내용은 Lie theory 개념 정리 포스트를 참조하면 된다.
\begin{equation}
\begin{aligned}
\mathbf{R} = \text{Exp}(\mathbf{w})
\end{aligned}
\end{equation}
- $\mathbf{R} \in SO(3)$
- $\mathbf{w} \in so(3)$
- $\text{Exp}(\mathbf{w}) = \exp([\mathbf{w}]_{\times})$
- $[\mathbf{w}]_{\times}$ : 3차원 벡터 $\mathbf{w}$의 반대칭행렬(skew-symmetric matrix)
임의의 작은 변화량 $\Delta \mathbf{w}$이 주어졌을 때 이를 기존 $\text{Exp}(\mathbf{w})$에 업데이트 하는 방법은 다음과 같은 두 가지 방법이 존재한다. 우선 [1] 기본적인 lie algebra를 사용한 업데이트 방법이 있다. 다음으로 [2] 섭동(perturbation) 모델을 활용한 업데이트 방법이 있다.
\begin{equation}
\begin{aligned}
\text{Exp}(\mathbf{w} + \Delta \mathbf{w}) \quad \cdots \text{[1]} \\
\text{Exp}(\mathbf{w}) \text{Exp}(\Delta \mathbf{w}) \quad \cdots \text{[2]}
\end{aligned}
\end{equation}
두 방법 사이에는 충분히 작은 $\Delta \mathbf{w}$에 대하여 다음과 같은 근사 변환 관계가 존재한다.
\begin{equation} \label{eq:app4}
\boxed{ \begin{aligned}
& \text{Exp}(\mathbf{w}+ \Delta \mathbf{w} ) \approx \text{Exp}(\mathbf{w}) \text{Exp}(\mathbf{J}_{r} \Delta \mathbf{w}) \\
&\text{Exp}(\mathbf{w}) \text{Exp}(\Delta \mathbf{w}) \approx \text{Exp}(\mathbf{w}+ \mathbf{J}_{r}^{-1}\Delta \mathbf{w} ) \\
\end{aligned} }
\end{equation}
- $\mathbf{J}_r = \mathbf{J}_r(\mathbf{w})$
- $\mathbf{J}_{r}(\mathbf{w}) = \mathbf{I} - \left( \frac{1 - \cos(\|\mathbf{w}\|)}{\|\mathbf{w}\|^2} \right) [\mathbf{w}]_\times + \left( \frac{\|\mathbf{w}\| - \sin(\|\mathbf{w}\|)}{\|\mathbf{w}\|^3} \right) [\mathbf{w}]_\times^2$ : SO(3)군의 오른쪽 자코비안(right jacobian)
- $\mathbf{J}_{r}(\mathbf{w})^{-1} = \mathbf{I} + \frac{1}{2}[\mathbf{w}]_\times + \Big( \frac{1}{\left\| \mathbf{w} \right\|^2} - \frac{1 + \cos(\left\| \mathbf{w} \right\|)}{2\left\| \mathbf{w} \right\|\sin(\left\| \mathbf{w} \right\|)} \Big) [\mathbf{w}]_\times^2$ : SO(3)군의 오른쪽 자코비안의 역행렬
위 식에서 $\mathbf{J}_{r}$을 SO(3)군의 오른쪽 자코비안(right jacobian)이라고 부르며 $\mathbf{J}_{r}^{-1}$을 SO(3)군의 오른쪽 자코비안의 역행렬(inverse right jacobian)이라고 부른다.
만약 업데이트 위치가 $\text{Exp}(\mathbf{w}) \text{Exp}(\Delta \mathbf{w})$처럼 오른쪽이 아닌 $\text{Exp}(\Delta \mathbf{w})\text{Exp}(\mathbf{w})$와 같이 왼쪽에 곱해진다면 위와 유사한 공식이 유도되며 그 때 나오는 자코비안은 SO(3)군의 왼쪽 자코비안(left jacobian) $\mathbf{J}_{l}$이라고 한다. $\mathbf{J}_{l}^{-1}$ 또한 동일하게 근사 식이 유도된다.
\begin{equation}
\begin{aligned}
& \text{Exp}(\mathbf{w}+ \Delta \mathbf{w} ) \approx \text{Exp}(\mathbf{J}_{l} \Delta \mathbf{w}) \text{Exp}(\mathbf{w}) \\
& \text{Exp}(\Delta \mathbf{w}) \text{Exp}(\mathbf{w}) \approx \text{Exp}(\mathbf{w}+ \mathbf{J}_{l}^{-1}\Delta \mathbf{w} ) \\
\end{aligned}
\end{equation}
- $\mathbf{J}_l = \mathbf{J}_l(\mathbf{w})$
- $\mathbf{J}_{l}(\mathbf{w}) = \mathbf{I} + \left( \frac{1 - \cos(\|\mathbf{w}\|)}{\|\mathbf{w}\|^2} \right) [\mathbf{w}]_\times + \left( \frac{\|\mathbf{w}\| - \sin(\|\mathbf{w}\|)}{\|\mathbf{w}\|^3} \right) [\mathbf{w}]_\times^2$ : SO(3)군의 왼쪽 자코비안(left jacobian)
- $\mathbf{J}_{l}(\mathbf{w})^{-1} = \mathbf{I} - \frac{1}{2}[\mathbf{w}]_\times + \Big( \frac{1}{\left\| \mathbf{w} \right\|^2} - \frac{1 + \cos(\left\| \mathbf{w} \right\|)}{2\left\| \mathbf{w} \right\|\sin(\left\| \mathbf{w} \right\|)} \Big) [\mathbf{w}]_\times^2$ : SO(3)군의 왼쪽 자코비안의 역행렬
두 자코비안 $\mathbf{J}_l, \mathbf{J}_r$ 사이에는 다음과 같은 변환 공식이 성립한다.
\begin{equation} \label{eq:app6}
\begin{aligned}
& \mathbf{J}_{l}(\omega) = \mathbf{J}_{r}(-\omega) = \mathbf{J}_{r}^{\intercal}(\omega) \\
& \mathbf{J}_{l}^{-1}(\omega) = \mathbf{J}_{r}^{-1}(-\omega) = \mathbf{J}_{r}^{-\intercal}(\omega)
\end{aligned}
\end{equation}
FAST-LIO2 논문의 수식 중 $\mathbf{A}$ 행렬은 왼쪽 자코비안 행렬 $\mathbf{J}_l$을 의미하며 $\mathbf{A}^{-1}$은 $\mathbf{J}_l^{-1}$을 의미한다.
7.2. Derivation of $\mathbf{F}_{\tilde{\mathbf{x}}}, \mathbf{F}_{\mathbf{w}}$
(\ref{eq:ikf2})의 에러 상태 변수를 다시 살펴보자.
\begin{equation}
\boxed{ \begin{aligned}
\tilde{\mathbf{x}} = \mathbf{x} \boxminus \bar{\mathbf{x}} = [\delta^{G} \boldsymbol{\theta}_{I}^{\intercal},\ ^{G}\tilde{\mathbf{p}}_{I}^{\intercal}, \ ^{G}\tilde{\mathbf{v}}_{I}^{\intercal}, \tilde{\mathbf{b}}_{w}^{\intercal}, \tilde{\mathbf{b}}_{a}^{\intercal}, \ ^{G}\tilde{\mathbf{g}}^{\intercal},\ \delta^{I} \boldsymbol{\theta}_{L}^{\intercal},\ ^{I}\tilde{\mathbf{p}}_{L}^{\intercal} ]^{\intercal} \in \mathbb{R}^{24}
\end{aligned} }
\end{equation}
- $\delta^{G} \boldsymbol{\theta}_{I} = \text{Log}(\ ^{G}\bar{\mathbf{R}}_{I}^{\intercal} \ ^{G}\mathbf{R}_{I}) \in \mathbb{R}^{3}$ : 월드좌표계에서 바라본 IMU의 회전에 대한 에러 상태 변수
- $\delta^{I} \boldsymbol{\theta}_{L} = \text{Log}(\ ^{I}\bar{\mathbf{R}}_{L}^{\intercal} \ ^{I}\mathbf{R}_{L}) \in \mathbb{R}^{3}$ : IMU 좌표계 바라본 LiDAR 센서의 회전에 대한 에러 상태 변수
Forward propagation 수식 (\ref{eq:fprop3})을 에러 상태 변수에 대한 식으로 변경하면 다음과 같다.
\begin{equation} \label{eq:app1}
\begin{aligned}
\tilde{\mathbf{x}}_{i+1} & = \mathbf{x}_{i+1} \boxminus \hat{\mathbf{x}}_{i+1} \\
& = (\mathbf{x}_i \boxplus \Delta t \mathbf{f}(\mathbf{x}_i, \mathbf{u}_i, \mathbf{w}_i)) \boxminus (\hat{\mathbf{x}}_i \boxplus \Delta t \mathbf{f}(\hat{\mathbf{x}}_i, \mathbf{u}_i, \mathbf{0})) \\
&
= \begin{bmatrix}
{\color{Mahogany} \text{Log}\bigg( \Big(\ ^{G}\hat{\mathbf{R}}_{I_i} \text{Exp}(\hat{\boldsymbol{\omega}}_i\Delta t) \Big)^{\intercal} \cdot
\Big(\ ^{G}\hat{\mathbf{R}}_{I_i} \text{Exp}\big(\ \delta^{G}\boldsymbol{\theta}_{I_i} \big) \text{Exp}(\boldsymbol{\omega}_i \Delta t) \Big) \bigg) } \\
^{G} \tilde{\mathbf{p}}_{I_i} +\ ^{G}\tilde{\mathbf{v}}_i \Delta t \\
^{G} \tilde{\mathbf{v}}_i + {\color{Mahogany} \Big(\ ^{G}\hat{\mathbf{R}}_{I_i}\text{Exp}\big(\ \delta^{G}\boldsymbol{\theta}_{I_i} \big)\Big) \mathbf{a}_i \Delta t } -\ ^{G}\hat{\mathbf{R}}_{I_i}\hat{\mathbf{a}}_i \Delta t + ^{G}\tilde{\mathbf{g}}_{i} \Delta t \\
\tilde{\mathbf{b}}_{w_i} + \mathbf{n}_{bw_i} \\
\tilde{\mathbf{b}}_{a_i} + \mathbf{n}_{ba_i} \\
^{G}\tilde{\mathbf{g}}_{i} \\
\delta^{I}\boldsymbol{\theta}_{L_i} \\
^{I}\tilde{\mathbf{p}}_{L_i} \\
\end{bmatrix}
\end{aligned}
\end{equation}
(\ref{eq:app1}) 첫번째 줄의 회전 $\delta \boldsymbol{\theta}$ 항은 다음과 같이 정리할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
& \text{Log}\bigg( \Big(\ ^{G}\hat{\mathbf{R}}_{I_i} \text{Exp}(\hat{\boldsymbol{\omega}}_i\Delta t) \Big)^{\intercal} \cdot
\Big(\ ^{G}\hat{\mathbf{R}}_{I_i} \text{Exp}\big(\ \delta^{G}\boldsymbol{\theta}_{I_i} \big) \text{Exp}(\boldsymbol{\omega}_i \Delta t) \Big) \bigg) \\
& = \text{Log}\Big( \text{Exp}(\hat{\boldsymbol{\omega}}_i\Delta t)^{\intercal} \cdot \Big(\text{Exp}(\delta^{G}\boldsymbol{\theta}_{I_i}) \cdot \text{Exp}( {\color{Mahogany} \boldsymbol{\omega}_i } \Delta t) \Big) \Big) \\
& = \text{Log}\Big( \text{Exp}(\hat{\boldsymbol{\omega}}_i\Delta t)^{\intercal} \cdot \Big(\text{Exp}(\delta^{G}\boldsymbol{\theta}_{I_i}) \cdot \text{Exp}({\color{Mahogany} (\hat{\boldsymbol{\omega}_i} - \tilde{\mathbf{b}}_{w_i} - \mathbf{n}_{w_i}) }
\Delta t) \Big) \Big) \\
& \approx \text{Log}\Big( \text{Exp}(\hat{\boldsymbol{\omega}}_i\Delta t)^{\intercal}\text{Exp}(\delta^{G}\boldsymbol{\theta}_{I_i}) \text{Exp}({\color{Mahogany} \hat{\boldsymbol{\omega}}_i } \Delta t) \cdot \text{Exp}(-\mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i\Delta t)({\color{Mahogany} \tilde{\mathbf{b}}_{w_i} + \mathbf{n}_{w_i} } ))\Big) \\
& \approx \text{Exp}(\hat{\boldsymbol{\omega}}_i\Delta t)^{\intercal} \delta^{G} \boldsymbol{\theta}_{I_i} - \mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i\Delta t)\tilde{\mathbf{b}}_{w_i} - \mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i \Delta t)\mathbf{n}_{w_i} \\
& \approx \text{Exp}(-\hat{\boldsymbol{\omega}}_i\Delta t) \delta^{G} \boldsymbol{\theta}_{I_i} - \mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i\Delta t) \tilde{\mathbf{b}}_{w_i} - \mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i \Delta t)\mathbf{n}_{w_i}
\end{aligned} }
\end{equation}
다음으로 (\ref{eq:app1}) 세번째 줄의 속도 $^{G}\tilde{\mathbf{v}}_{I_i}$ 항의 중간 부분은 다음과 같이 정리할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
& \Big(\ ^{G}\hat{\mathbf{R}}_{I_i} {\color{Mahogany} \text{Exp}\big(\ \delta^{G} \boldsymbol{\theta}_{I_i} \big) } \Big) \mathbf{a}_i \Delta t \\
& \approx \Big(\ ^{G}\hat{\mathbf{R}}_{I_i} {\color{Mahogany} \big( \mathbf{I} + [\delta^{G} \boldsymbol{\theta}_{I_i}]_{\times} \big) } \Big) (\hat{\mathbf{a}}_{i} - \tilde{\mathbf{b}}_{a_i} - \mathbf{n}_{a_i}) \Delta t \\
& \approx\ ^{G}\hat{\mathbf{R}}_{I_i}\hat{\mathbf{a}}_{i}\Delta t -\ ^{G}\hat{\mathbf{R}}_{I_i}\tilde{\mathbf{b}}_{a_i}\Delta t -\ ^{G}\hat{\mathbf{R}}_{I_i}\mathbf{n}_{a_i}\Delta t -\ ^{G}\hat{\mathbf{R}}_{I_i}[\hat{\mathbf{a}}_{i}]_{\times}\delta^{G} \boldsymbol{\theta}_{I_i} \Delta t
\end{aligned} }
\end{equation}
유도 과정을 그림으로 나타내면 다음과 같다.


지금까지 유도된 식을 정리하여 에러 상태 변수를 다시 쓰면 (\ref{eq:fprop1}) 식이 유도된다.
\begin{equation} \label{eq:app2}
\boxed{ \begin{aligned}
\begin{bmatrix}
\delta^{G} \boldsymbol{\theta}_{I_{i+1}} \\
^{G}\tilde{\mathbf{p}}_{I_{i+1}} \\
^{G}\tilde{\mathbf{v}}_{I_{i+1}} \\
\tilde{\mathbf{b}}_{w_{i+1}} \\
\tilde{\mathbf{b}}_{a_{i+1}} \\
^{G}\tilde{\mathbf{g}}_{i+1} \\
\delta^{I} \boldsymbol{\theta}'_{L_{i+1}}\\
^{I}\tilde{\mathbf{p}}_{L_{i+1}}
\end{bmatrix}
& = \begin{bmatrix}
\text{Exp}(-\hat{\boldsymbol{\omega}}_i\Delta t) {\color{Mahogany} \delta^{G} \boldsymbol{\theta}_{I_i} } - \mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i\Delta t) {\color{Mahogany} \tilde{\mathbf{b}}_{w_i} } - \mathbf{J}_{r}(\hat{\boldsymbol{\omega}}_i \Delta t){\color{Mahogany} \mathbf{n}_{w_i} } \\
^{G} {\color{Mahogany} \tilde{\mathbf{p}}_{I_i} } +\ {\color{Mahogany} ^{G}\tilde{\mathbf{v}}_i } \Delta t \\
{\color{Mahogany} ^{G} \tilde{\mathbf{v}}_i } -\ ^{G}\hat{\mathbf{R}}_{I_i}[\hat{\mathbf{a}}_{i}]_{\times} {\color{Mahogany}\delta^{G} \boldsymbol{\theta}_{I_i} }\Delta t -\ ^{G}\hat{\mathbf{R}}_{I_i}{\color{Mahogany} \tilde{\mathbf{b}}_{a_i} } \Delta t -\ ^{G}\hat{\mathbf{R}}_{I_i}{\color{Mahogany} \mathbf{n}_{a_i} } \Delta t + {\color{Mahogany} ^{G}\tilde{\mathbf{g}}_{i} } \Delta t \\
{\color{Mahogany} \tilde{\mathbf{b}}_{w_i} + \mathbf{n}_{bw_i} } \\
{\color{Mahogany} \tilde{\mathbf{b}}_{a_i} + \mathbf{n}_{ba_i} } \\
{\color{Mahogany} ^{G}\tilde{\mathbf{g}}_{i} } \\
{\color{Mahogany} \delta^{I} \boldsymbol{\theta}_{L_i} } \\
{\color{Mahogany} ^{I}\tilde{\mathbf{p}}_{L_i} } \\
\end{bmatrix} \\
& =
\begin{bmatrix}
\text{Exp}(-\hat{\boldsymbol{\omega}}_i \Delta t){\color{Mahogany} \delta^{G} \boldsymbol{\theta}_{I_i} } -\mathbf{J}_r(\hat{\boldsymbol{\omega}}_i \Delta t) {\color{Mahogany} \tilde{\mathbf{b}}_{w_i} } \Delta t \\
{\color{Mahogany} ^{G}\tilde{\mathbf{p}}_{I_i} +\ ^{G}\tilde{\mathbf{v}}_{I_i} } \Delta t \\
{\color{Mahogany} ^{G}\tilde{\mathbf{v}}_{I_i} } +\ ^{G}\hat{\mathbf{R}}_{I_i}(-[\hat{\mathbf{a}}_i]_{\times}{\color{Mahogany} \delta^{G} \boldsymbol{\theta}_{I_i} - \tilde{\mathbf{b}}_{a_i} } )\Delta t + {\color{Mahogany} ^{G}\tilde{\mathbf{g}}_{i} } \Delta t \\
{\color{Mahogany} \tilde{\mathbf{b}}_{w_i} } \\
{\color{Mahogany} \tilde{\mathbf{b}}_{a_i} } \\
{\color{Mahogany} ^{G}\tilde{\mathbf{g}}_{i} } \\
{\color{Mahogany} \delta^{I} \boldsymbol{\theta}_{L_i} } \\
{\color{Mahogany} ^{I}\tilde{\mathbf{p}}_{L_{i}} }
\end{bmatrix}
+ \begin{bmatrix}
-\mathbf{J}_r(\hat{\boldsymbol{\omega}}_i \Delta t) {\color{Mahogany} \mathbf{n}_{w_i} } \Delta t \\
\mathbf{0} \\
-^{G}\hat{\mathbf{R}}_{I_i} {\color{Mahogany} \mathbf{n}_{a_i} } \Delta t \\
{\color{Mahogany} \mathbf{n}_{bw_i} } \Delta t \\
{\color{Mahogany} \mathbf{n}_{ba_i} } \Delta t \\
\mathbf{0} \\
\mathbf{0}\\
\mathbf{0}
\end{bmatrix} \\
\end{aligned} }
\end{equation}
\begin{equation} \label{eq:app3}
\boxed{ \begin{aligned}
& \begin{bmatrix}
\delta^{G} \boldsymbol{\theta}_{I_{i+1}} \\
^{G}\tilde{\mathbf{p}}_{I_{i+1}} \\
^{G}\tilde{\mathbf{v}}_{I_{i+1}} \\
\tilde{\mathbf{b}}_{w_{i+1}} \\
\tilde{\mathbf{b}}_{a_{i+1}} \\
^{G}\tilde{\mathbf{g}}_{i+1} \\
\delta^{I}\boldsymbol{\theta}'_{L_{i+1}}\\
^{I}\tilde{\mathbf{p}}_{L_{i+1}}
\end{bmatrix} = \begin{bmatrix}
\text{Exp}(-\hat{\boldsymbol{\omega}}_i \Delta t) & \mathbf{0} & \mathbf{0} & -\mathbf{J}_r(\hat{\boldsymbol{\omega}}_i \Delta t)\Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0}& \mathbf{0} \\
\mathbf{0} & \mathbf{I} & \mathbf{I}\Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0}& \mathbf{0}& \mathbf{0} \\
-^{G}\hat{\mathbf{R}}_{I_i}[\hat{\mathbf{a}}_i]_{\times}\Delta t & \mathbf{0} &\mathbf{I} & \mathbf{0} & -^{G}\hat{\mathbf{R}}_{I_i}\Delta t & \mathbf{I}\Delta t& \mathbf{0}& \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} & \mathbf{0} & \mathbf{0}& \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0} & \mathbf{0}& \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0}& \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I} & \mathbf{0}
\\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}
\end{bmatrix} {\color{Mahogany} \begin{bmatrix}
\delta^{G} \boldsymbol{\theta}_{I_i} \\
^{G}\tilde{\mathbf{p}}_{I_{i}} \\
^{G}\tilde{\mathbf{v}}_{I_{i}} \\
\tilde{\mathbf{b}}_{w_{i}} \\
\tilde{\mathbf{b}}_{a_{i}} \\
^{G}\tilde{\mathbf{g}}_{i} \\
\delta^{I} \boldsymbol{\theta}_{L_i}\\
^{I}\tilde{\mathbf{p}}_{L_{i}}
\end{bmatrix} } \\
& \qquad\qquad\qquad\qquad\qquad + \begin{bmatrix}
-\mathbf{J}_r(\hat{\boldsymbol{\omega}}_i \Delta t) \Delta t & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & -^{G}\hat{\mathbf{R}}_{I_i}\Delta t & \mathbf{0} & \mathbf{0}\\
\mathbf{0} & \mathbf{0} & \mathbf{I}\Delta t & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}\Delta t \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0}
\end{bmatrix} {\color{Mahogany}
\begin{bmatrix}
\mathbf{n}_{w_i} \\
\mathbf{n}_{a_i} \\
\mathbf{n}_{bw_i} \\
\mathbf{n}_{ba_i} \\
\end{bmatrix} }
\\ & \therefore \tilde{\mathbf{x}}_{i+1} \approx \mathbf{F}_{\tilde{\mathbf{x}}}\tilde{\mathbf{x}}_{i} + \mathbf{F}_{\mathbf{w}}\mathbf{w}_{i} \\
\end{aligned} }
\end{equation}
R2Live 논문의 Appendix 수식 유도 과정을 보면 위 식의 $\mathbf{J}_r$ 부분이 $\mathbf{J}_r^{\intercal}$이라고 나와 있으나 오타인 것으로 보인다. 자세한 내용은 해당 github issue 링크를 참조하면 된다.
(ㅇㅇ님 댓글로 내용 수정 24.05.29)
FAST-LIO2의 (\ref{eq:fprop1}) 식은 왼쪽 자코비안(left jacobian) $\mathbf{J}_l$을 사용하여 표현하였기 때문에 (\ref{eq:app6}) 변환 관계에 따라 $\mathbf{J}_r \rightarrow \mathbf{J}_l^{\intercal}$이 적용되었다.
7.3. Derivation of $\mathbf{H}_{j}^{\kappa}$
다음으로 (\ref{eq:iupdate1}) 식의 $\mathbf{H}_{j}^{\kappa}$를 유도해보자.
\begin{equation}
\begin{aligned}
0 &=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L}(\ ^{L}\mathbf{p}_{j} +\ ^{L}\mathbf{n}_{j}) -\ ^{G}\mathbf{q}_{j}) \\
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{p}_{j}^{\text{gt}} -\ ^{G}\mathbf{q}_{j}) \\ & = \mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j}) \\
& \approx \mathbf{h}_{j}(\hat{\mathbf{x}}^{\kappa}_{k},0) +\mathbf{H}_{j}^{\kappa} \tilde{\mathbf{x}}_{k}^{\kappa} + \mathbf{v}_j \\
\end{aligned}
\end{equation}
에러 상태에 대한 자코비안 $\mathbf{H}_{j}^{\kappa}$는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{j}^{\kappa} = \frac{\partial \mathbf{h}_{j}(\hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa},\ ^{L}\mathbf{n}_{j})
}{\partial \tilde{\mathbf{x}}_{k}^{\kappa}}\bigg|_{\tilde{\mathbf{x}}_{k}^{\kappa}=0}
\end{aligned}
\end{equation}
우선 $\mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j})$를 자세히 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{h}_{j}(\mathbf{x}_{k},\ ^{L}\mathbf{n}_{j}) &=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L_k}{\color{Mahogany} (\ ^{L}\mathbf{p}_{j} +\ ^{L}\mathbf{n}_{j}) } -\ ^{G}\mathbf{q}_{j}) \\
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\mathbf{T}_{I_k}\ ^{I}\mathbf{T}_{L_k}\ {\color{Mahogany} ^{L}\mathbf{p}_{j}^{gt} } -\ ^{G}\mathbf{q}_{j}) \\
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}{\mathbf{R}}_{I_k}(\ ^{I}{\mathbf{R}}_{L_k}\ {\color{Mahogany} ^{L}\mathbf{p}_{j}^{gt} } + ^{I}{\mathbf{p}}_{L_k} ) +\ ^{G}{\mathbf{p}}_{I_k} -\ ^{G}\mathbf{q}_{j}) \\
\end{aligned}
\end{equation}
- $^{G}\mathbf{T}_{I_k} = [^{G}{\mathbf{R}}_{I_k},\ ^{G}{\mathbf{p}}_{I_k}]$
- $^{I}\mathbf{T}_{L_k} = [^{I}{\mathbf{R}}_{L_k},\ ^{I}{\mathbf{p}}_{L_k}]$
$\mathbf{x}_{k} = \hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa}$를 대입하여 에러 상태 변수까지 고려하여 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{h}_{j}(\hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa},\ ^{L}\mathbf{n}_{j})
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa} {\color{Cyan} \text{Exp}(\delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa}) } (\ ^{I}\hat{\mathbf{R}}_{L_k}^{\kappa}\ {\color{Mahogany} ^{L}\mathbf{p}_{j}^{gt} } + ^{I}\hat{\mathbf{p}}_{L_k}^{\kappa} ) +\ ^{G}\hat{\mathbf{p}}_{I_k}^{\kappa} +\ {\color{Cyan} ^{G}\tilde{\mathbf{p}}_{I_k}^{\kappa} } -\ ^{G}\mathbf{q}_{j}) \\
\end{aligned}
\end{equation}
수식의 앞 부분은 다음과 같이 정리할 수 있다.
\begin{equation}
\begin{aligned}
^{G}\hat{\mathbf{R}}_{I_k}^{\kappa} {\color{Cyan} \text{Exp}(\delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa}) } \mathbf{P}_{a}
& \approx\ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa} {\color{Cyan} (\mathbf{I} + [\delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa}]_{\times} ) } \mathbf{P}_{a} \\
& = \ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa}\mathbf{P}_{a} -\ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa}[\mathbf{P}_{a}]_{\times}\delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa}
\end{aligned}
\end{equation}
- $\mathbf{P}_{a} = (\ ^{I}\hat{\mathbf{R}}_{L_k}^{\kappa}\ {\color{Mahogany} ^{L}\mathbf{p}_{j}^{gt} } + ^{I}\hat{\mathbf{p}}_{L_k}^{\kappa})$
그림으로 나타내면 다음과 같다.

정리한 수식을 다시 대입하면 다음과 같이 전개된다.
\begin{equation}
\begin{aligned}
\mathbf{h}_{j}(\hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa},\ ^{L}\mathbf{n}_{j})
&=\ ^{G}\mathbf{u}_{j}^{\intercal}(\ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa}\mathbf{P}_{a} -\ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa}[\mathbf{P}_{a}]_{\times}{\color{Mahogany} \delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa} } +\ ^{G}\hat{\mathbf{p}}_{I_k}^{\kappa} +\ {\color{Mahogany} ^{G}\tilde{\mathbf{p}}_{I_k}^{\kappa} } -\ ^{G}\mathbf{q}_{j}) \\
\end{aligned}
\end{equation}
$\mathbf{H}_{j}^{\kappa} = \frac{\partial \mathbf{h}_{j}(\hat{\mathbf{x}}_{k}^{\kappa} \boxplus \tilde{\mathbf{x}}_{k}^{\kappa},\ ^{L}\mathbf{n}_{j})
}{\partial \tilde{\mathbf{x}}_{k}^{\kappa}}\bigg|_{\tilde{\mathbf{x}}_{k}^{\kappa}=0}$이므로 위 수식을 에러 상태 변수에 대해 편미분하면 다음과 같은 자코비안 행렬 $\mathbf{H}_{j}^{\kappa}$를 얻을 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{H}_{j}^{\kappa} =\ ^{G}\mathbf{u}_j^{\intercal} \Big[ -^{G}\hat{\mathbf{R}}_{I_k}^{\kappa}[\mathbf{P}_{a}]_{\times} \ \ \mathbf{I}_{3\times 3}, \ \ \mathbf{0}_{3\times 18} \Big] \in \mathbb{R}^{1\times 24}
\end{aligned} }
\end{equation}
7.4. Derivation of $\mathbf{J}^{\kappa}$
다음으로 (\ref{eq:iupdate4})의 $\mathbf{J}^{\kappa}$를 구해보자. 이는 주로 [3]의 Appendix B를 참고하여 작성하였다.
\begin{equation}
\begin{aligned}
\mathbf{J}^{\kappa} & = \frac{\partial (\hat{\mathbf{x}}_k^{\kappa} \boxplus \tilde{\mathbf{x}}_k^{\kappa}) \boxminus \hat{\mathbf{x}}_k}{\partial \tilde{\mathbf{x}}_k^{\kappa}}
\end{aligned}
\end{equation}
에러 상태 변수 $\tilde{\mathbf{x}}_k^{\kappa}$에서 회전 SO(3)군을 제외한 나머지 선형 상태 변수는 $\boxplus, \boxminus$가 사라지므로 다음과 같이 쉽게 구할 수 있다.
\begin{equation}
\begin{aligned}
\frac{\partial (\hat{\mathbf{x}}_k^{\kappa} + \tilde{\mathbf{x}}_k^{\kappa}) - \hat{\mathbf{x}}_k}{\partial \tilde{\mathbf{x}}_k^{\kappa}} & = \frac{\partial \tilde{\mathbf{x}}_k^{\kappa}}{\partial \tilde{\mathbf{x}}_k^{\kappa}} \\
& = \mathbf{I}_{18\times 18}
\end{aligned}
\end{equation}
따라서 에러 상태 변수 $\tilde{\mathbf{x}}_k^{\kappa}$에서 선형 부분은 제외하고 비선형 회전 SO(3)군만 있다고 가정한 후 수식을 유도한다. 우선, $(\hat{\mathbf{x}}_k^{\kappa} \boxplus \tilde{\mathbf{x}}_k^{\kappa}) \boxminus \hat{\mathbf{x}}_k$ 부분을 $\mathbf{w}$로 치환한다.
\begin{equation}
\begin{aligned}
\mathbf{w} & = (\hat{\mathbf{x}}_k^{\kappa} \boxplus \tilde{\mathbf{x}}_k^{\kappa}) \boxminus \hat{\mathbf{x}}_k \\
& = \text{Log}(\hat{\mathbf{x}}_k^{\intercal}(\hat{\mathbf{x}}_k^{\kappa} \cdot \text{Exp}(\tilde{\mathbf{x}}_k^{\kappa})))
\end{aligned}
\end{equation}
- $\mathbf{R} \boxplus \mathbf{r} : \mathbf{R} \cdot \text{Exp}(\mathbf{r})$
- $\mathbf{R}_1 \boxminus \mathbf{R}_2 : \text{Log}(\mathbf{R}_2^{\intercal}\mathbf{R}_1)$
- $\hat{\mathbf{x}}_k =\ ^{G}\hat{\mathbf{R}}_{I_k} \in SO(3)$
- $\hat{\mathbf{x}}_k^{\kappa} =\ ^{G}\hat{\mathbf{R}}_{I_k}^{\kappa} \in SO(3)$
위 식에 지수 매핑(exponential mapping)을 적용하고 기호를 단순화한다.
\begin{equation}
\begin{aligned}
\text{Exp}(\mathbf{w}) & = {\mathbf{y}}^{\intercal}({\mathbf{x}} \cdot \text{Exp}({\mathbf{u}}))
\end{aligned}
\end{equation}
- $\mathbf{x} = \hat{\mathbf{x}}_k^{\kappa}$
- $\mathbf{u} = \tilde{\mathbf{x}}_k^{\kappa}$
- $\mathbf{y} = \hat{\mathbf{x}}_k$
작은 증분량 $\Delta \mathbf{u}$를 우측 항에 더하는 것은 좌측 항에 $\Delta \mathbf{w}$를 더하는 것과 같다.
\begin{equation} \label{eq:app5}
\begin{aligned}
\text{Exp}(\mathbf{w} + \Delta \mathbf{w}) & = {\mathbf{y}}^{\intercal}({\mathbf{x}} \cdot \text{Exp}(\mathbf{u} + \Delta \mathbf{u}))
\end{aligned}
\end{equation}
작은 증분량에 대하여 (\ref{eq:app4})이 성립한다.
\begin{equation}
\begin{aligned}
\text{Exp}(\mathbf{w} + \Delta \mathbf{w}) & = \text{Exp}(\mathbf{w})\text{Exp}(\mathbf{J}_{r}(\mathbf{w})\Delta \mathbf{w}) \\
& \approx \text{Exp}(\mathbf{w}) \Big( \mathbf{I} + [\mathbf{J}_r(\mathbf{w})\Delta\mathbf{w} ]_{\times} \Big)
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\text{Exp}(\mathbf{u} + \Delta \mathbf{u}) & = \text{Exp}(\mathbf{u})\text{Exp}(\mathbf{J}_{r}(\mathbf{u})\Delta \mathbf{u}) \\
& \approx \text{Exp}(\mathbf{u}) \Big( \mathbf{I} + [\mathbf{J}_r(\mathbf{u})\Delta\mathbf{u} ]_{\times} \Big)
\end{aligned}
\end{equation}
따라서 (\ref{eq:app5}) 식은 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
\text{Exp}(\mathbf{w}) \Big( \mathbf{I} + [\mathbf{J}_r(\mathbf{w})\Delta\mathbf{w} ]_{\times} \Big) & = {\color{Mahogany} \mathbf{y}^{\intercal}\mathbf{x} \cdot \text{Exp}(\mathbf{u}) } \Big( \mathbf{I} + [\mathbf{J}_r(\mathbf{u})\Delta\mathbf{u} ]_{\times} \Big) \\
\text{Exp}(\mathbf{w}) \Big( \mathbf{I} + [\mathbf{J}_r(\mathbf{w})\Delta\mathbf{w} ]_{\times} \Big) & = {\color{Mahogany} \text{Exp}(\mathbf{w}) } \Big( \mathbf{I} + [\mathbf{J}_r(\mathbf{u})\Delta\mathbf{u} ]_{\times} \Big) \\
\mathbf{I} + [\mathbf{J}_r(\mathbf{w})\Delta\mathbf{w} ]_{\times} & = \mathbf{I} + [\mathbf{J}_r(\mathbf{u})\Delta\mathbf{u} ]_{\times} \\
\end{aligned}
\end{equation}
- $\text{Exp}(\mathbf{w}) = \mathbf{y}^{\intercal}\mathbf{x} \cdot \text{Exp}(\mathbf{u})$
위 마지막 줄의 식을 정리하면 다음 식이 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{J}_r(\mathbf{w})\Delta\mathbf{w} & = \mathbf{J}_r(\mathbf{u})\Delta\mathbf{u} \\
& = \Delta\mathbf{u} \\
\end{aligned}
\end{equation}
- $\mathbf{J}_r(\mathbf{u}) = \mathbf{I}_{3\times 3}$ : $\tilde{\mathbf{x}}_k^{\kappa}=\mathbf{0}$ 시점에 대한 자코비안이므로 $\mathbf{J}_r(\mathbf{0}) = \mathbf{I}_{3\times 3}$이 된다.
결론적으로 회전 SO(3)군에 대한 $\mathbf{J}^{\kappa}$는 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{J}^{\kappa} & = \frac{\partial (\hat{\mathbf{x}}_k^{\kappa} \boxplus \tilde{\mathbf{x}}_k^{\kappa}) \boxminus \hat{\mathbf{x}}_k}{\partial \tilde{\mathbf{x}}_k^{\kappa}} \\
& = \frac{\Delta \mathbf{w}}{\Delta \mathbf{u}} \\
& = \mathbf{J}_r^{-1}(\mathbf{w}) \\
& = \mathbf{J}_r^{-1}(\delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa}) \quad \cdots \text{ for } \delta^{G}\boldsymbol{\theta}_{I_k}^{\kappa} \\
& = \mathbf{J}_r^{-1}(\delta^{I}\boldsymbol{\theta}_{L_k}^{\kappa}) \quad \cdots \text{ for } \delta^{I}\boldsymbol{\theta}_{L_k}^{\kappa}
\end{aligned} }
\end{equation}
하지만 FAST-LIO2 논문의 (11) 식에서 보다시피 왼쪽 자코비안(left jacobian)을 통해 표현하였기 때문에 (\ref{eq:app6})의 $\mathbf{J}_r^{-1} = \mathbf{J}_l^{-\intercal}$ 변환 관계를 사용하여 왼쪽 자코비안(left jacobian) $\mathbf{J}_l^{-\intercal}(\cdot)$으로 변환하였다. 최종 식은 (\ref{eq:iupdate4})을 참조하면 된다.
(ㅇㅇ님 댓글로 수정 완료. 24.05.29)
7.5. Derivation of $\tilde{\mathbf{x}}_{k}^{\kappa}$
다음으로 FAST-LIO2의 IKF 과정 중 업데이트 스텝부터 $\tilde{\mathbf{x}}_{k}^{\kappa}$까지 중간 과정을 유도해보자. 이는 주로 링크의 내용을 참고하여 유도하였다. 수식 유도 과정이 길고 복잡하기 때문에 아래와 같이 색상으로 강조하여 표현하였다.


8. References
'Engineering' 카테고리의 다른 글
| [SLAM] ROVIO 논문 및 코드 리뷰 (+ IEKF) (0) | 2024.01.27 |
|---|---|
| [SLAM] VINS-mono 논문 리뷰 (+ IMU preintegration) (23) | 2022.10.15 |
| [MVG] Stereo Camera Calibration 예제코드 및 설명 (C++) (3) | 2022.07.14 |
| [MVG] Scene Plane-based Homography 예제코드 및 설명 (C++) (0) | 2022.07.07 |
| [MVG] Vanishing Point-based Metric Rectification 예제코드 및 설명 (C++) (0) | 2022.07.03 |
 A L I D A
A L I D A





