본 포스트는 공부 목적으로 작성하였습니다.
혹시 보시는 도중 잘못된 부분이나 개선할 부분이 있다면 댓글이나 메일주시면 확인 후 수정하도록 하겠습니다.
본 포스트에서는 feature-based VO를 기반으로 reprojection 에러를 최소화하여 bundle adjustment(BA)를 수행하는 과정에 대해 설명한다.
Bundle adjustment

두 개의 이미지 사이의 매칭점 쌍들이 주어진 경우 8-point 알고리즘을 사용하여 fundamental matrix $\mathbf{F}$를 추정할 수 있다. 만약 캘리브레이션된 카메라의 경우 $\mathbf{F}$를 통해 essential matrix $\mathbf{E}$를 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{E} = \mathbf{K}^{T}\mathbf{F}\mathbf{K}
\end{aligned}
\end{equation}
- $\mathbf{K} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \\ 0 & 0 & 1 \end{bmatrix}$ : 카메라 내부(intrinsic) 파라미터. $f$는 초점거리를 의미하고 $c_{x}, c_{y}$는 주점(principal point)을 의미한다.
다음으로 $\mathbf{E}$에서 두 카메라 간 상대 포즈 $[\mathbf{R} | \mathbf{t}]$를 분해하여 구할 수 있다. 이를 분해하는 자세한 내용은 DecomposeFundamentalMatrix 함수 또는 1.8. Extraction of cameras from the essential matrix를 참조하면 된다.
\begin{equation}
\begin{aligned}\mathbf{E} \rightarrow [\mathbf{R} | \mathbf{t}] \quad (\text{ extract from } \mathbf{E} = \mathbf{t}^{\wedge}\mathbf{R})\end{aligned}
\end{equation}

이렇게 구한 두 카메라의 포즈 $[\mathbf{R} | \mathbf{t}]$를 바탕으로 triangulation 알고리즘을 사용하여 매칭점 쌍들에 대한 3차원 점을 계산할 수 있다.

BA는 위 그림과 같이 연속적인 카메라 영상 + 매칭 쌍이 주어졌을 때 카메라 포즈 전체와 월드 상 점들 전체에 대한 최적의 위치를 찾는 방법을 말한다. 이 때, 특징점을 사용하는 VO의 특성 상 reprojection 에러를 최소화하여 카메라 포즈와 3차원 점들을 최적화한다.

Reprojection error
NOMENCLATURE of reprojection error
- $\tilde{\mathbf{p}} = \pi_{h}(\cdot) : \begin{bmatrix} X' \\ Y' \\ Z' \\1 \end{bmatrix} \rightarrow \begin{bmatrix} X'/Z' \\ Y'/Z' \\ 1 \end{bmatrix} = \begin{bmatrix} \tilde{u} \\ \tilde{v} \\ 1 \end{bmatrix}$
- 이미지 평면에 프로젝션하기 위해 3차원 공간 상의 점 $\mathbf{X}'$를 non-homogeneous 변환한 점
- $\hat{\mathbf{p}} = \pi_{k}(\cdot) = \tilde{\mathbf{K}} \tilde{\mathbf{p}} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \end{bmatrix} \begin{bmatrix} \tilde{u} \\ \tilde{v} \\ 1 \end{bmatrix}= \begin{bmatrix} f\tilde{u} + c_{x} \\ f\tilde{v} + c_{y} \end{bmatrix} = \begin{bmatrix} u \\ v \end{bmatrix}$
- 렌즈 왜곡을 보정한 후 이미지 평면에 프로젝션한 점. 만약 왜곡 보정이 입력 단계에서 이미 수행된 경우 $\pi_{k}(\cdot) = \tilde{\mathbf{K}}(\cdot)$이 된다.
- $\mathbf{K} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \\ 0 & 0 & 1 \end{bmatrix}$: 카메라 내부(intrinsic) 파라미터
- $\tilde{\mathbf{K}} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \end{bmatrix}$: $\mathbb{P}^{2} \rightarrow \mathbb{R}^{2}$로 프로젝션하기 위해 내부 파라미터의 마지막 행을 생략했다.
- $\mathcal{X} = [\mathcal{T}_{1}, \cdots, \mathcal{T}_{m}, \mathbf{X}_{1}, \cdots, \mathbf{X}_{n}]^{\intercal}$: 모델의 상태변수
- $m$ : 카메라 포즈의 개수
- $n$: 3차원 점의 개수
- $\mathcal{T}_{i} = [\mathbf{R}_{i}, \mathbf{t}_{i}]$
- $\mathbf{e}_{ij} = \mathbf{e}_{ij}(\mathcal{X})$: 간략한 표기를 위해 $\mathcal{X}$ 생략하기도 한다
- $\mathbf{p}_{ij}$: 관측된(observed) 특정짐의 픽셀 좌표
- $\hat{\mathbf{p}}_{ij}$: 예측된(estimated) 특징점의 픽셀 좌표
- $\mathbf{T}_{i}\mathbf{X}_{j}$: Transformation, 3차원 점 $\mathbf{X}_{j}$를 카메라 좌표계 $\{i\}$로 변환, $\bigg( \mathbf{T}_{i}\mathbf{X}_{j} = \begin{bmatrix} \mathbf{R}_{i} \mathbf{X}_{j} + \mathbf{t}_{i} \\ 1 \end{bmatrix} \in \mathbb{R}^{4\times1} \bigg)$
- $\mathbf{X}' = \mathbf{TX} = [X', Y', Z',1]^{\intercal} = [\tilde{\mathbf{X}}', 1]^{\intercal} $
- $\oplus$ : SO(3) 회전행렬 $\mathbf{R}$과 3차원 벡터 $\mathbf{t}, \mathbf{X}$를 한 번에 업데이트할 수 있는 연산자.
- $\mathbf{J} = \frac{\partial \mathbf{e}}{\partial \mathcal{X}} = \frac{\partial \mathbf{e}}{\partial [\mathcal{T}, \mathbf{X}]}$
- $\mathbf{w} = \begin{bmatrix} w_{x}&w_{y}&w_{z} \end{bmatrix}^{\intercal}$: 각속도
- $[\mathbf{w}]_{\times} = \begin{bmatrix} 0 & -w_{z} & w_{y} \\ w_{z} & 0 & -w_{x} \\ -w_{y} & w_{x} & 0 \end{bmatrix}$ : 각속도 $\mathbf{w}$의 반대칭 행렬
본 섹션에서는 BA에서 사용하는 reprojection 에러를 정의하고 이를 통해 최적화를 수행하는 과정에 대해 설명한다.
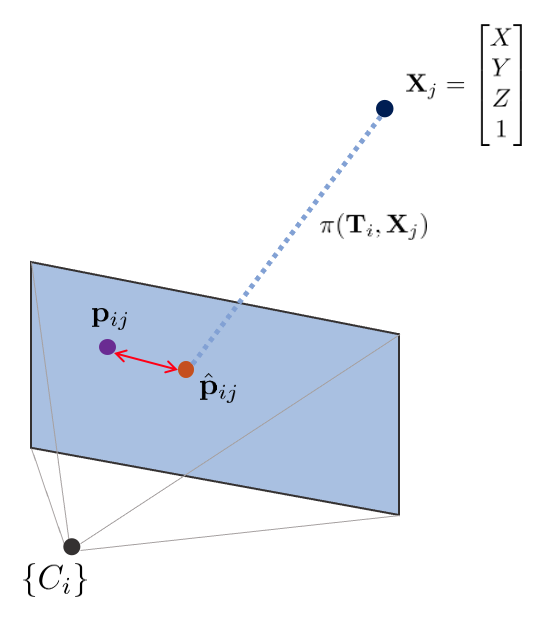
i번째 핀홀카메라 $\{C_{i}\}$의 포즈 $\mathbf{T}_{i}$와 j번째 월드 상의 한 점 $\mathbf{X}_{j}$가 있을 때 $\mathbf{X}_{j}$는 다음과 같은 변환을 통해 이미지 평면 상에 투영된다.
\begin{equation}
\begin{aligned}
\text{projection model: }\quad\hat{\mathbf{p}}_{ij} = \pi(\mathbf{T}_{i}, \mathbf{X}_{j})
\end{aligned}
\end{equation}

위와 같이 카메라 내부/외부(intrinsic/extrinsic) 파라미터를 활용한 모델을 projection model이라고 한다. 이를 통한 reprojection 에러는 다음과 같이 정의한다.
\begin{equation}
\boxed{
\begin{aligned}
\mathbf{e}_{ij} & = \mathbf{p}_{ij} - \hat{\mathbf{p}}_{ij} \\
& = \mathbf{p}_{ij} - \pi(\mathbf{T}_{i}, \mathbf{X}_{j}) \\
& = \mathbf{p}_{ij} - \pi_{k}(\pi_{h}(\mathbf{T}_{i}\mathbf{X}_{j}))
\end{aligned} }
\end{equation}
모든 카메라 포즈, 3차원 점들에 대한 cost function은 다음과 같이 정의된다.
\begin{equation}
\begin{aligned}
\mathbf{E}(\mathcal{X}) & = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \left\| \mathbf{e}_{ij} \right\|^{2} \\
& = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \mathbf{e}_{ij}^{\intercal}\mathbf{e}_{ij} \\
& = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} (\mathbf{p}_{ij} - \hat{\mathbf{p}}_{ij})^{\intercal}(\mathbf{p}_{ij} - \hat{\mathbf{p}}_{ij})
\end{aligned} \label{eq:10}
\end{equation}
$\mathbf{E}(\mathcal{X}^{*})$를 만족하는 $\left\|\mathbf{e}(\mathcal{X}^{*})\right\|^{2}$를 non-linear least squares를 통해 반복적으로 계산할 수 있다. 작은 증분량 $\Delta \mathcal{X}$를 반복적으로 $\mathcal{X}$에 업데이트함으로써 최적의 상태를 찾는다.
\begin{equation}
\begin{aligned}
\mathbf{E}(\mathcal{X} + \Delta \mathcal{X}) & = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \left\|\mathbf{e}(\mathcal{X} +\Delta \mathcal{X})\right\|^{2}
\end{aligned}
\end{equation}
엄밀하게 말하면 상태 증분량 $\Delta \mathcal{X}$은 SO(3) 회전행렬을 포함하므로 $\oplus$ 연산자를 통해 기존 상태 $\mathcal{X}$에 더해지는게 맞지만 표현의 편의를 위해 $+$ 연산자를 사용하였다.
\begin{equation}
\begin{aligned}
\mathbf{e}( \mathcal{X} \oplus \Delta \mathcal{X})
\quad \rightarrow \quad\mathbf{e}(\mathcal{X} + \Delta \mathcal{X})
\end{aligned}
\end{equation}
위 식은 테일러 1차 근사를 통해 다음과 같이 표현이 가능하다.
\begin{equation}
\begin{aligned}
\mathbf{e}(\mathcal{X} + \Delta \mathcal{X}) & \approx \mathbf{e}(\mathcal{X}) + \mathbf{J}\Delta \mathcal{X} \\ & = \mathbf{e}(\mathcal{X}) + \mathbf{J}_{c} \Delta \mathcal{T} + \mathbf{J}_{p} \Delta \mathbf{X} \\
& = \mathbf{e}(\mathcal{X}) + \frac{\partial \mathbf{e}}{\partial \mathcal{T}} \Delta \mathcal{T} + \frac{\partial \mathbf{e}}{\partial \mathbf{X}}\Delta \mathbf{X} \\
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{E}(\mathcal{X} + \Delta \mathcal{X}) & \approx \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \left\|\mathbf{e}(\mathcal{X}) + \mathbf{J}\Delta \mathcal{X} \right\|^{2} \\
\end{aligned}
\end{equation}
이를 미분하여 최적의 증분량 $\Delta \mathcal{X}^{*}$ 값을 구하면 다음과 같다. 자세한 유도 과정은 본 문서에서는 생략한다. 유도 과정에 대해 자세히 알고 싶으면 [SLAM] Errors and Jacobian Derivations for SLAM 정리 포스트를 참조하면 된다.
\begin{equation}
\begin{aligned}
& \mathbf{J}^{\intercal}\mathbf{J} \Delta \mathcal{X}^{*} = -\mathbf{J}^{\intercal}\mathbf{e} \\
& \mathbf{H}\Delta \mathcal{X}^{*} = - \mathbf{b} \\
\end{aligned} \label{eq:6}
\end{equation}
Jacobian of the reprojection error
본 섹션에서는 reprojection 에러를 최적화할 때 사용하는 자코비안을 구하는 과정에 대해 설명한다. cost function (\ref{eq:10})에서 최적화 할 상태변수 $\mathcal{X} = [\mathcal{T}_{1},\cdots,\mathcal{T}_{m},\mathbf{X}_{1},\cdots,\mathbf{X}_{n}]^{\intercal}$는 다음 그림과 같다.
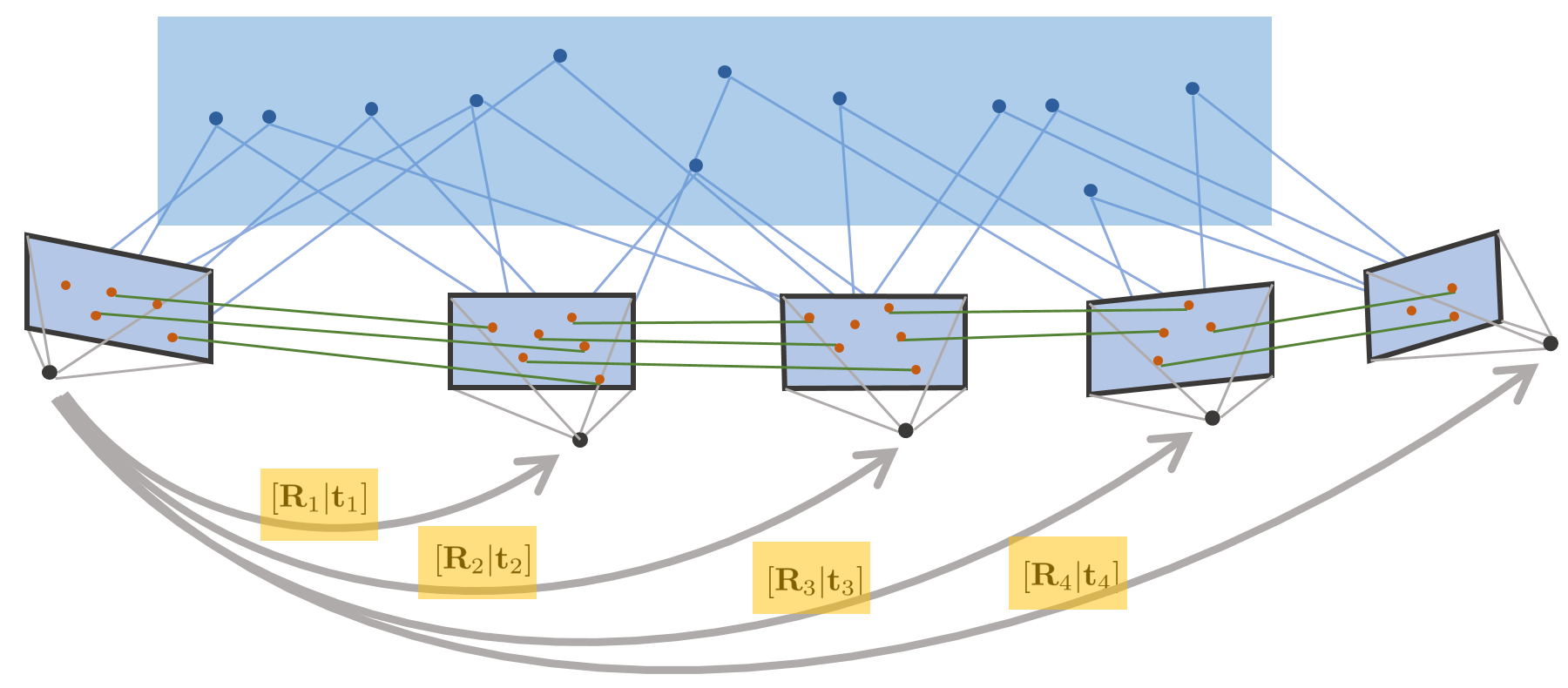
카메라 포즈와 3차원 점을 둘로 나누면 다음과 같다.

$\mathbf{e}(\mathcal{X}+\Delta \mathcal{X})$에 1차 테일러 근사를 수행하면 다음과 같은 자코비안 $\mathbf{J}$가 유도된다.


이를 토대로 hessian matrix $\mathbf{H}$를 다시 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{J}^{T}\mathbf{J}
=
\begin{bmatrix}
\mathbf{J}_{\mathbf{c}}^{T}\mathbf{J}_{\mathbf{c}} & \mathbf{J}_{\mathbf{c}}^{T}\mathbf{J}_{\mathbf{p}}\\
\mathbf{J}_{\mathbf{p}}^{T}\mathbf{J}_{\mathbf{c}} & \mathbf{J}_{\mathbf{p}}^{T}\mathbf{J}_{\mathbf{p}}
\end{bmatrix} =
\begin{bmatrix}
\mathbf{H}_{cc} & \mathbf{H}_{cp}\\
\mathbf{H}_{pc} & \mathbf{H}_{pp}
\end{bmatrix}
\end{aligned}
\end{equation}
카메라 포즈에 대한 자코비안 $\mathbf{J}_{c}$는 다음과 같다.
\begin{equation} \boxed{ \begin{aligned} \mathbf{J}_{c} & = \frac{\partial \hat{\mathbf{p}}}{\partial \tilde{\mathbf{p}}} \frac{\partial \tilde{\mathbf{p}}}{\partial \mathbf{X}'} \frac{\partial \mathbf{X}'}{\partial [\Delta \mathbf{w}, \mathbf{t}]} \\ & = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \end{bmatrix} \begin{bmatrix} \frac{1}{Z'} & 0 & \frac{-X'}{Z'^{2}} & 0 \\ 0 & \frac{1}{Z'} & \frac{-Y'}{Z'^{2}} & 0 \\ 0 & 0 & 0 &0 \end{bmatrix} \begin{bmatrix} 0 & Z' & -Y' & 1 & 0 & 0 \\ -Z' & 0 & X' & 0 & 1 & 0 \\ Y' & -X' & 0 & 0 & 0 & 1 \\ 0&0&0&0&0&0 \end{bmatrix} \\ & = \begin{bmatrix} \frac{f}{Z'} & 0 & -\frac{fX}{Z'^{2}} & 0 \\ 0 & \frac{f}{Z'} & -\frac{fY}{Z'^{2}} & 0\end{bmatrix} \begin{bmatrix} 0 & Z' & -Y' & 1 & 0 & 0 \\ -Z' & 0 & X' & 0 & 1 & 0 \\ Y'& -X'& 0 & 0 & 0 & 1 \\ 0&0&0&0&0&0 \end{bmatrix} \\ & = \begin{bmatrix} -\frac{fX'Y'}{Z'^{2}} & \frac{f(1 + X'^{2})}{Z'^{2}} & -\frac{fY'}{Z'} & \frac{f}{Z'} & 0 & -\frac{fX'}{Z'^{2}} \\ -\frac{f(1+y^{2})}{Z'^{2}} & \frac{fX'Y'}{Z'^{2}} & \frac{fX'}{Z'} & 0 & \frac{f}{Z'} & -\frac{fY'}{Z'^{2}} \end{bmatrix} \in \mathbb{R}^{2 \times 6} \end{aligned} } \end{equation}
3차원 공간 상의 점에 대한 자코비안 $\mathbf{J}_{p}$는 다음과 같다.
\begin{equation}
\boxed{
\begin{aligned}
\mathbf{J}_{p} & = \begin{bmatrix} \frac{f}{Z'} & 0 & -\frac{fX'}{Z'^{2}} \\ 0 & \frac{f}{Z'} & -\frac{fY'}{Z'^{2}} \end{bmatrix} \mathbf{R} \in \mathbb{R}^{2\times 3}
\end{aligned} }
\end{equation}
자세한 자코비안의 유도 과정은 [SLAM] Errors and Jacobian Derivations for SLAM 정리 포스트를 참조하면 된다.
Sparsity of hessian matrix
카메라 포즈, 3차원 점이 여러 개인 일반적인 경우 자코비안은 다음과 같다.

3차원 점 $\mathbf{X}_{j}$는 카메라 위치 $\mathbf{T}_{i}$에서만 보이고 해당 블록만 0이 아닌 값을 갖는다. 이렇게 행렬에 대부분이 0으로 채워져 있는 특성을 jacobian sparsity 특성이라고 한다. 자코비안의 이러한 sparse 특성으로 인해 자코비안의 곱인 hessian matrix $\mathbf{H}$ 또한 sparsity 특성을 갖는다. (Freiburg Univ. https://youtu.be/wVsfCnyt5jA 참조)
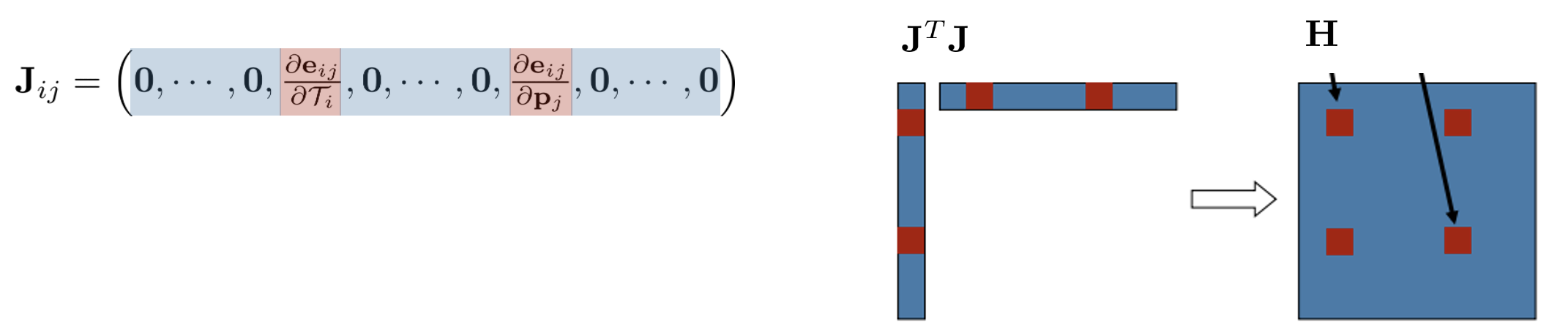
$\mathbf{H}$를 전개하면 다음과 같다.
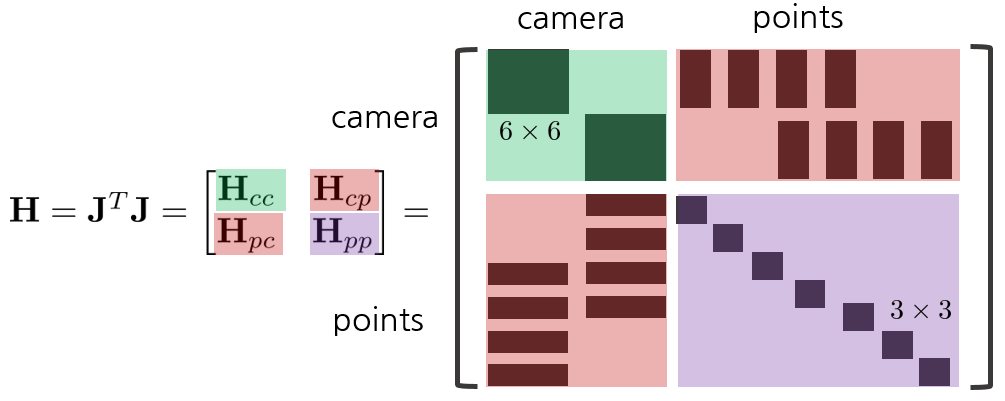
하지만 일반적인 경우 3차원 점의 개수가 카메라 포즈보다 훨씬 많으므로 다음과 같은 거대한 $\mathbf{H}$ 행렬이 생성된다. 따라서 (\ref{eq:6})에서 $\Delta \mathcal{X}^{*} = -\mathbf{H}^{-1} \mathbf{b}$ 역행렬을 계산할 때 매우 큰 연산시간이 소요되므로 이를 빠르게 개선할 다른 방법이 필요하다.

Schur complement
이 때, schur complement 변환 트릭을 사용하면 연산량을 낮출 수 있다. schur complement는 marginalization을 수행하기 위한 행렬 변환 트릭을 말한다. schur complement 방법의 핵심은 $\Delta \mathcal{X}_{c}$, $\Delta \mathcal{X}_{p}$를 동시에 계산하지 않고 순차적으로 하나씩 계산함으로써 연산량을 낮추는 것이다.
\begin{equation} \begin{aligned}
\mathbf{H} \Delta \mathcal{X}^{*} & = - \mathbf{b} \\
\begin{bmatrix}
\mathbf{H}_{cc} & \mathbf{H}_{cp} \\
\mathbf{H}_{pc} & \mathbf{H}_{pp}
\end{bmatrix}
\begin{bmatrix}
\Delta \mathcal{X}_{c} \\
\Delta \mathcal{X}_{p}
\end{bmatrix}
& = \begin{bmatrix}
\mathbf{b}_{c}\\
\mathbf{b}_{p}
\end{bmatrix}
\end{aligned} \end{equation}
Forward substitution
$\Delta \mathcal{X}_{c}$를 먼저 계산한다. 우선 선형시스템에서 $\mathbf{H}_{cp}$를 제거하기 위해 양변에 아래와 같은 행렬곱을 수행한다.

위 행렬을 전개하면 아래와 같이 (1,2) 원소가 0이 되는 행렬이 만들어진다. 이를 marginalization이라고 한다.

위 노란색 부분만 곱하면 $\Delta \mathcal{X}_{p}$ 없이 오직 카메라 포즈 증분량 $\Delta \mathcal{X}_{c}$만을 계산할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{H}_{m}\Delta \mathcal{X}_{c} = \mathbf{b}_{m}
\end{aligned} \end{equation}
- $\mathbf{H}_{m}=\mathbf{H}_{cc}-\mathbf{H}_{cp}\mathbf{H}_{pp}^{-1}\mathbf{H}_{pc}$
- $\mathbf{b}_{m}=\mathbf{b}_{c} - \mathbf{H}_{cp}\mathbf{H}_{pp}^{-1}\mathbf{b}_{p}$
이는 3차원 공간 상의 점 $p$와 관련된 hessian matrix $\mathbf{H}_{pp}, \mathbf{H}_{pc}, \mathbf{H}_{cp}$가 marginalized out되서 모든 정보가 새로운 행렬 $\mathbf{H}_{m}, \mathbf{b}_{m}$에 업데이트되고 소멸된 것을 의미한다.
Backward substitution
앞서 $\Delta \mathcal{X}_{c}$를 계산한 값을 토대로 $\Delta \mathcal{X}_{p}$를 계산한다.

위 파란색 부분을 계산할 때 이전 단계에서 이미 모든 변수의 값을 구했으므로 단순하게 연산이 가능하다.
\begin{equation} \begin{aligned}
\Delta \mathcal{X}_{p} = \mathbf{H}_{pp}^{-1}(\mathbf{b}_{p}-\mathbf{H}_{pc}\Delta \mathcal{X}_{c})
\end{aligned} \end{equation}
Linear solvers & robust cost functions
앞서 유도한 schur complement 방법을 통해 얻은 방정식을 실제로 계산하기 위해서는 선형대수학의 테크닉들이 사용된다.
\begin{equation} \begin{aligned}
\mathbf{H}_{m}\Delta \mathcal{X}_{c} = \mathbf{b}_{m}
\end{aligned} \end{equation}
이는 선형방정식 $\mathbf{A}\mathbf{x} = \mathbf{b}$ 형태이므로 LU decompostion, cholesky decompostion 등 다양한 방법을 사용하여 빠르게 행렬 계산을 수행할 수 있다. 또한 huber 같은 robust cost function을 사용하여 outlier의 영향력을 줄일 수 있다.
References
- [youtube] SLAMKR Online Study
- [youtube] Robot Mapping Coure - Freiburg Univ
- [blog] [SLAM] Bundle Adjustment의 Jacobian 계산 - jinyongjeong님 블로그
'Fundamental' 카테고리의 다른 글
| 선형대수학 (Linear Algebra) 개념 정리 Part 2 (1) | 2022.06.18 |
|---|---|
| [SLAM] Optical Flow와 Direct Method 개념 및 코드 리뷰 (0) | 2022.06.16 |
| [SLAM] Feature-based와 Direct method VO 개념 비교 (0) | 2022.06.02 |
| [SLAM] Pose Graph Optimization 개념 설명 및 예제 코드 분석 (20) | 2022.01.05 |
| 다중관점기하학(Multiple View Geometry in Computer Vision) 책 내용 정리 Part 3 (0) | 2022.01.05 |
 A L I D A
A L I D A





