5.Error-state kinematics for IMU-driven systems
5.1 Motivation
본 섹션에서는 에러 상태 방정식(error-state equations)을 통해 노이즈와 bias가 포험된 IMU의 가속도와 각속도를 표현하는 방법에 대해 설명한다. 이 때, 회전 표기법은 Hamilton 쿼터니언을 사용하였다. 일반적으로 가속도와 각속도는 IMU 센서를 통해 입력받으며 이를 누적하여 포즈를 추적하는 방법을 dead-reckoning이라고 한다. Dead-reckoning은 시간에 따라 에러가 누적되어 드리프트되는 현상이 발생하므로 이러한 문제를 해결하기 위해 일반적으로 카메라나 GPS 센서 정보를 퓨전하여 사용한다.
Error-state Kalman Filter(ESKF)는 앞서 설명한 dead-reckoning과 센서 퓨전에 사용되는 유용한 도구 중 하나이다. 칼만 필터의 패러다임을 사용하는 ESKF는 다음과 같은 성질들이 존재한다 (Madyastha el tal., 2011):
- 방향(orientation)에 대한 에러 상태 표현법이 최소한의 파라미터를 가진다. 즉, 자유도만큼의 최소 파라미터를 가지기 때문에 over-parameterized로 인해 발생하는 특이점(signularity) 같은 현상이 발생하지 않는다.
- 에러 상태 시스템은 항상 원점(origin) 근처에서만 동작한다. 따라서 짐벌락 같은 파라미터 특이점 현상이 발생하지 않으며 항상 선형화를 수행할 수 있다.
- 에러 상태는 일반적으로 값이 작기 때문에 2차항 이상의 값들은 무시할 수 있다. 이는 자코비안 연산을 쉽고 빠르게 수행할 수 있도록 도와준다. 몇몇 자코비안은 상수화하여 사용하기도 한다.
- 에러 방정식은 일반적으로 비선형을 가진 큰 값들이 nominal 상태에서 처리되므로 속도가 느린 편이다. 이는 KF correction 스텝이 prediction 스텝보다 느린 속도로 적용할 수 있다는 것을 의미한다.
5.2 The error-state Kalman filter explained
ESKF에는 true, nominal, error의 세가지 상태가 존재한다. true 상태는 nominal과 error 상태를 적절하게 조합하여 표현할 수 있다. nominal 상태는 일반적으로 큰 값들로 구성되며 비선형성을 가지고 error 상태는 작은 값들로 구성되며 선형성을 가진다.
ESKF는 다음과 같이 동작한다. 우선, 고속으로 들어오는 IMU 데이터 $\mathbf{u}_{m}$은 nominal 상태 $\mathbf{x}$에 적분된다. 이 때, nominal 상태는 노이즈 항 $\mathbf{w}$를 고려하지 않고 적분한다. 따라서 시간이 지날수록 적분된 nominal 상태는 에러가 증가하게 된다. 노이즈와 섭동(perturbation)을 포함한 에러는 error 상태 $\delta \mathbf{x}$에 누적되고 추후 ESKF 시스템에 의해 처리된다. error 상태는 작은 값들로 구성되어 있으며 nominal 상태에서 계산된 행렬들과 함께 선형 시스템으로 표현할 수 있다. nominal 상태에서 값이 적분됨과 동시에 error 상태에 대한 가우시안 추정을 수행한다. 이를 prediction 스텝이라고 하며 해당 스텝에서는 아직 추정치를 개선할 수 있는 관측값들이 입력되지 않았으므로 오직 추정만 수행한다. 다음으로 IMU를 제외한 카메라 또는 GPS와 같은 다른 관측 값들이 들어오면 correction 스텝을 진행한다. correction 스텝은 일반적으로 IMU의 적분 속도보다 매우 느린 속도로 진행된다. correction 스텝을 수행하면 error 상태에 대한 posterior를 구할 수 있다. 다음으로 업데이트 된 error 상태의 평균값이 nominal 상태에 적용되고 error 상태는 0으로 리셋한다. 마지막으로 리셋을 반영하기 위한 error 상태의 공분산 행렬이 업데이트 되며 ESKF의 한 사이클이 종료된다. ESKF는 이러한 과정을 계속 반복하면서 실행된다.
5.3 System kinematics in continuous time
ESKF에서 사용하는 모든 변수들의 정의는 아래 테이블에 요약하였다.
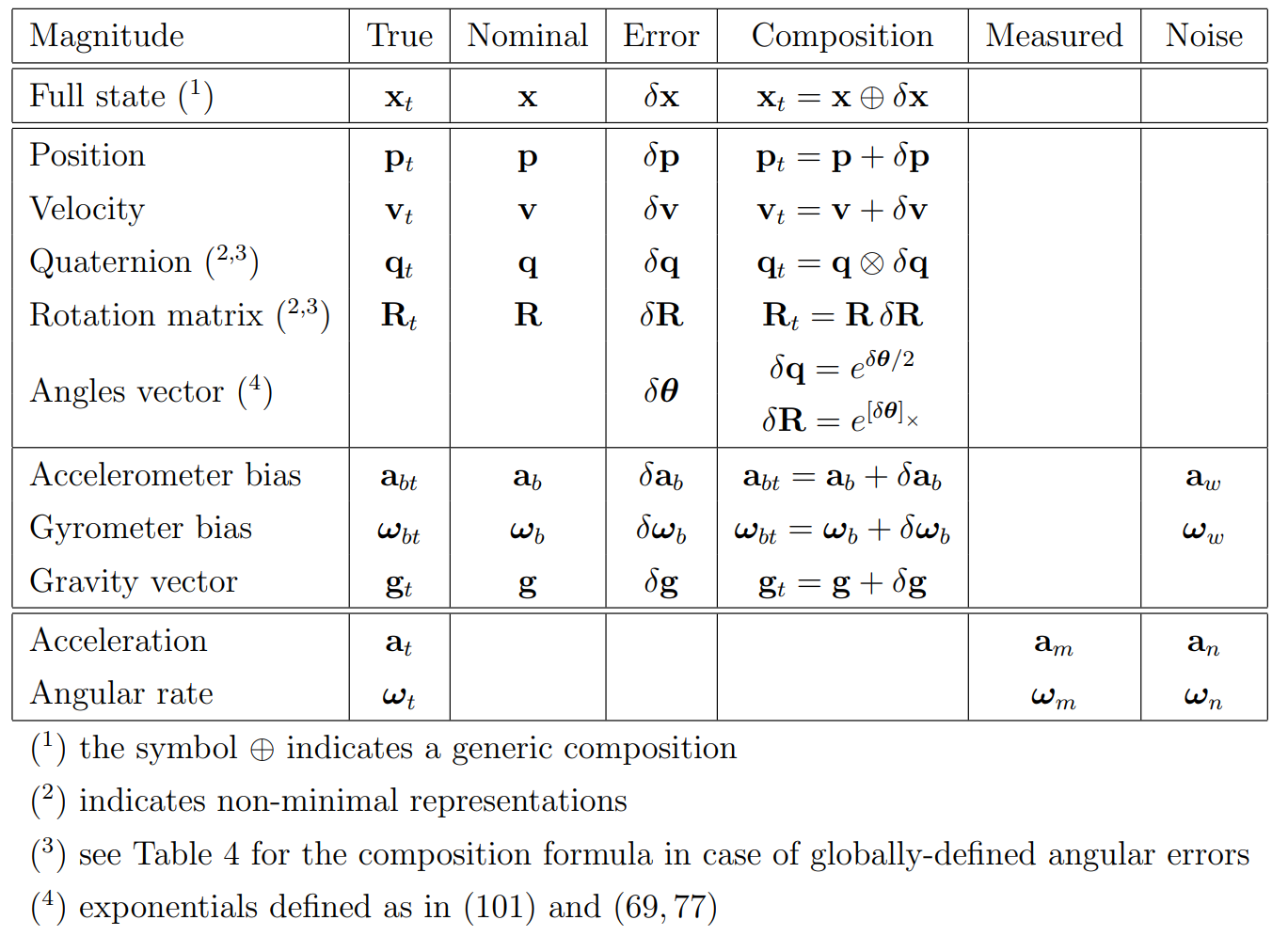
수식을 전개하기 전에 두 개의 중요한 규약(convention)에 대해 언급하면 다음과 같다.
- nominal 상태를 표현할 때 사용하는 각속도 $\boldsymbol{\omega}$는 지역적(locally) 의미의 각속도로 정의한다. 즉, 월드 좌표계에서 바라 본 각속도를 의미하는 것이 아닌 현재 IMU 좌표계에서 각속도를 의미한다. 이러한 규약을 통해 IMU 센서에서 들어오는 각속도 값인 $\boldsymbol{\omega}_{m}$을 바로 사용할 수 있는 이점이 있다.
- 각 에러(angular error) $\delta \boldsymbol{\theta}$ 또한 지역적 의미의 각 에러로 정의된다. 이러한 규약이 최적의 성능을 주는 표현법은 아니지만 대다수의 IMU 필터링 작업에서 지역적으로 표현하였기 때문에 이를 사용한다. (Li and Mourikis, 2012)에 따르면 전역적(globally)으로 정의된 각 에러가 더 좋은 성능을 보여주는 것을 확인했다. 전역적 정의에 대한 내용은 섹션 7에서 설명한다.
5.3.1 The true-state kinematics
true 상태 방정식은 다음과 같다.
\begin{equation}
\begin{aligned}
& \dot{\mathbf{p}}_{t} = \mathbf{v}_{t} \\
& \dot{\mathbf{v}}_{t} = \mathbf{a}_{t} \\
& \dot{\mathbf{q}}_{t} = \frac{1}{2} \mathbf{q}_{t} \otimes \boldsymbol{\omega}_{t} \\
& \dot{\mathbf{a}}_{bt} = \mathbf{a}_{\omega} \\
& \dot{\boldsymbol{\omega}}_{bt} = \boldsymbol{\omega}_{\omega} \\
& \dot{\mathbf{g}}_{t} = 0
\end{aligned}
\end{equation}
true 가속도 $\mathbf{a}_{t}$와 각속도 $\boldsymbol{\omega}_{t}$는 IMU 센서 데이터에서 나온 측정 가속도와 각속도 $\mathbf{a}_{m}, \boldsymbol{\omega}_{m}$으로부터 구할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{a}_{m} = \mathbf{R}^{\intercal}_{t} (\mathbf{a}_{t} - \mathbf{g}_{t}) + \mathbf{a}_{bt} + \mathbf{a}_{n} \\
& \boldsymbol{\omega}_{m} = \boldsymbol{\omega}_{t} + \boldsymbol{\omega}_{bt} + \boldsymbol{\omega}_{n}
\end{aligned}
\end{equation}
이 때, $\mathbf{R}_{t} \triangleq \mathbf{R}\{\mathbf{q}_{t}\}$이다. 위 식을 정리하면 다음과 같이 true 가속도와 각속도를 구할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{a}_{t} = \mathbf{R}_{t} (\mathbf{a}_{m} - \mathbf{a}_{bt} - \mathbf{a}_{n}) + \mathbf{g}_{t} \\
& \boldsymbol{\omega}_{t} = \boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{bt} - \boldsymbol{\omega}_{n}
\end{aligned}
\end{equation}
위 식을 대입하여 true 상태 방정식을 다시 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \dot{\mathbf{p}}_{t} = \mathbf{v}_{t} \\
& \dot{\mathbf{v}}_{t} = \mathbf{R}_{t} (\mathbf{a}_{m} - \mathbf{a}_{bt} - \mathbf{a}_{n}) + \mathbf{g}_{t} \\
& \dot{\mathbf{q}}_{t} = \frac{1}{2} \mathbf{q}_{t} \otimes (\boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{bt} - \boldsymbol{\omega}_{n}) \\
& \dot{\mathbf{a}}_{bt} = \mathbf{a}_{\omega} \\
& \dot{\boldsymbol{\omega}}_{bt} = \boldsymbol{\omega}_{\omega} \\
& \dot{\mathbf{g}}_{t} = 0
\end{aligned} \label{eq:56}
\end{equation}
위 식은 $\dot{\mathbf{x}}_{t} = f_{t}(\mathbf{x}_{t}, \mathbf{u}, \mathbf{w})$와 같이 함수로 표현할 수 있다. true 상태 $\mathbf{x}_{t}$는 노이즈가 포함된 IMU 센서 데이터 $\mathbf{u}_{m}$의 영향을 받으며 white gaussian noise $\mathbf{w}$가 포함된다. 입력 파라미터를 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{x}_{t} = \begin{bmatrix}
\mathbf{p}_{t} \\ \mathbf{v}_{t} \\ \mathbf{q}_{t} \\ \mathbf{a}_{bt} \\ \boldsymbol{\omega}_{bt} \\ \mathbf{g}_{t}
\end{bmatrix} & \quad \mathbf{u} = \begin{bmatrix}
\mathbf{a}_{m} - \mathbf{a}_{n} \\ \boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{n}
\end{bmatrix} & \quad \mathbf{w} = \begin{bmatrix}
\mathbf{a}_{\omega} \\ \boldsymbol{\omega}_{\omega}
\end{bmatrix}
\end{aligned}
\end{equation}
위 식에서 중력 벡터 $\mathbf{g}_{t}$ 또한 필터에 의해 추정되는 것을 확인할 수 있다. 중력은 이미 값을 알고 있는 상수이므로 이를 미분한 값은 0이 된다. 시스템은 일반적으로 랜덤한 임의의 방향(orientation) $\mathbf{q}_{t}(t=0) = \mathbf{q}_{0}$에서 시작하기 때문에 초기 중력 벡터의 값은 알 수 없다. 일반적으로 시스템의 시작 지점이 곧 월드 좌표계의 원점이므로 $\mathbf{q}_{0} = (1,0,0,0)$이고 $\mathbf{R}_{0} = \mathbf{R}\{\mathbf{q}_{0} = \mathbf{I} \}$라고 하자. 이 때, 우리는 지면과 평행한 임의의 $\mathbf{q}_{t}$ 프레임이 아닌 $\mathbf{q}_{0}$ 프레임에서 바라 본 중력 벡터 $\mathbf{g}_{t}$를 추정하고자 한다. 따라서 노이즈로 인한 초기 방향의 불확정성이 초기 중력 벡터의 불확정성에도 영향을 미친다. (\ref{eq:56})의 $\dot{\mathbf{v}}_{t}$ 항은 불확정성을 포함하는 $\mathbf{g}$에 대해 선형이다. 또한 초기 방향 $\mathbf{q}_{0}$는 이미 알고 있는 값이고 불확정성이 존재하지 않으므로 $\mathbf{q}$는 불확정성이 없는 상태에서 시작한다. 이후 중력 벡터가 추정되고 중력에 수평한 평면이 예측되면 모든 상태와 궤적(trajectory)를 중력에 맞게 방향을 재조절할 수 있다 (Lupton and Sukkarieh, 2009). 이러한 방향 재조절은 옵션 사항으로 독자가 원한다면 상태 방정식에서 중력 관련된 항을 제거할 수 있다. 그리고 일반적으로 사용하는 $\mathbf{g} \triangleq (0,0,-9.8xx)$와 같이 설정하고 $xx$는 독자의 실험의 정확도에 맞게 설정할 수 있다.
5.3.2 The nominal-state kinematics
nominal 상태 방정식은 노이즈와 섭동(perturbation)이 없는 상태로 모델링한다.
\begin{equation}
\begin{aligned}
& \dot{\mathbf{p}} = \mathbf{v} \\
& \dot{\mathbf{v}} = \mathbf{R} (\mathbf{a}_{m} - \mathbf{a}_{b}) + \mathbf{g} \\
& \dot{\mathbf{q}} = \frac{1}{2} \mathbf{q} \otimes (\boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b}) \\
& \dot{\mathbf{a}}_{b} = 0 \\
& \dot{\boldsymbol{\omega}}_{b} = 0 \\
& \dot{\mathbf{g}} = 0
\end{aligned}
\end{equation}
5.3.3 The error-state kinematics
다음으로 error 상태 방정식에 대해 설명한다. 테이블 \ref{fig:3}을 보면 각각 상태 방정식에 따라 2차항 이상의 작은 값들을 생략한 합성(composition)에 대해 정리하였다. 해당 섹션에서는 모든 error 상태 방정식을 우선적으로 소개하고 이에 대한 유도 및 증명 과정은 추후에 기술한다.
\begin{equation}
\begin{aligned}
& \dot{\delta\mathbf{p}} = \delta\mathbf{v} \\
& \dot{\delta\mathbf{v}} = -\mathbf{R}[\mathbf{a}_{m} - \mathbf{a}_{b}]_{\times} \delta \boldsymbol{\theta} - \mathbf{R}\delta \mathbf{a}_{b} + \delta \mathbf{g} - \mathbf{R}\mathbf{a}_{n} \\
& \dot{\delta\boldsymbol{\theta}} = -[\boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b}]_{\times} \delta \boldsymbol{\theta} - \delta \boldsymbol{\omega}_{b} - \boldsymbol{\omega}_{n} \\
& \dot{\delta\mathbf{a}}_{b} = \mathbf{a}_{\omega} \\
& \dot{\delta\boldsymbol{\omega}}_{b} = \boldsymbol{\omega}_{\omega} \\
& \dot{\delta\mathbf{g}} = 0
\end{aligned} \label{eq:57}
\end{equation}
위 식 중 $\dot{\delta\mathbf{p}}, \dot{\delta\mathbf{a}}_{b}, \dot{\delta\boldsymbol{\omega}}_{b}, \dot{\delta\mathbf{g}}$ 항은 선형 방정식으로부터 유도된 자명한 값들이다. 하지만 $\dot{\delta\mathbf{v}}, \dot{\delta\boldsymbol{\theta}}$ 항은 비선형적인 $\dot{\mathbf{p}}_{t}, \dot{\mathbf{v}}_{t}, \dot{\mathbf{p}}, \dot{\mathbf{v}}$ 식으로부터 선형화된 식을 얻기 위해 별도의 유도 과정이 필요하다.
Equation (\ref{eq:57}): The linear velocity error 속도 에러 $\dot{\delta\mathbf{v}}$를 구하기 위해 다음과 같은 식으로부터 시작한다.
\begin{equation}
\begin{aligned}
& \mathbf{R}_{t} = \mathbf{R}(\mathbf{I} + [\delta \boldsymbol{\theta}]_{\times}) + O(\left\| \delta \boldsymbol{\theta} \right\|^{2}) \\
& \dot{\mathbf{v}} = \mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{g}
\end{aligned}
\end{equation}
$\mathbf{R}_{t}$ 식은 회전량이 작을 때 이를 근사하는 식을 의미하며 $\dot{\mathbf{v}}$ 식은 nominal 상태의 $\dot{\mathbf{v}}$ 식을 $\mathbf{a}_{\mathcal{B}}$와 $\delta \mathbf{a}_{\mathcal{B}}$를 통해 나타낸 식이다. $\mathbf{a}_{\mathcal{B}}$와 $\delta\mathbf{a}_{\mathcal{B}}$는 body 프레임의 가속도를 의미하며 다음과 같이 정의할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{a}_{\mathcal{B}} \triangleq \mathbf{a}_{m} - \mathbf{a}_{b} \\
& \delta \mathbf{a}_{\mathcal{B}} \triangleq -\delta \mathbf{a}_{b} - \mathbf{a}_{n}
\end{aligned} \label{eq:58}
\end{equation}
이를 통해 true 가속도 $\mathbf{a}_{t}$을 다시 나타내면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{a}_{t} = \mathbf{R}_{t}(\mathbf{a}_{\mathcal{B}} + \delta \mathbf{a}_{\mathcal{B}}) + \mathbf{g} + \delta \mathbf{g}
\end{aligned}
\end{equation}
식 (\ref{eq:56})에서 $\dot{\mathbf{v}}_{t}$는 다음과 같이 나타날 수 있고 이 때 $O(\left| \delta \boldsymbol{\theta}\right|^{2})$항은 무시한다.
\begin{equation}
\begin{aligned}
\dot{\mathbf{v}} + \dot{\delta \mathbf{v}} & = \boxed{ \dot{\mathbf{v}}_t} && = \mathbf{R}(\mathbf{I} + [\delta \boldsymbol{\theta}]_{\times})(\mathbf{a}_{\mathcal{B}} + \delta \mathbf{a}_{\mathcal{B}}) + \mathbf{g} + \delta \mathbf{g} \\
\mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{g} + \dot{\delta\mathbf{v}} & = && = \mathbf{Ra}_{\mathcal{B}} + \mathbf{R}\delta\mathbf{a}_{\mathcal{B}} + \mathbf{R}[\delta \boldsymbol{\theta}]_{\times} \mathbf{a}_{\mathcal{B}} +\mathbf{R}[\delta\boldsymbol{\theta}]_{\times} \delta \mathbf{a}_{\mathcal{B}} +\mathbf{g} + \delta \mathbf{g}
\end{aligned}
\end{equation}
위 식 양 변의 $\mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{g}$ 항을 제거하면 다음과 같다.
\begin{equation}
\begin{aligned}
\dot{\delta\mathbf{v}} = \mathbf{R}(\delta \mathbf{a}_{\mathcal{B}} - [\mathbf{a}_{\mathcal{B}}]_{\times}\delta \boldsymbol{\theta}) + \delta \mathbf{g}
\end{aligned}
\end{equation}
식 (\ref{eq:58})을 사용하여 풀어서 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\dot{\delta\mathbf{v}} = \mathbf{R}(-[\mathbf{a}_{m}-\mathbf{a}_{b}]_{\times}\delta\boldsymbol{\theta} -\delta \mathbf{a}_{b} - \mathbf{a}_{n}) + \delta \mathbf{g}
\end{aligned}
\end{equation}
위 식을 전개하면 속도 에러에 대한 식을 얻을 수 있다.
\begin{equation}
\boxed{
\begin{aligned}
\dot{\delta\mathbf{v}} = -\mathbf{R}[\mathbf{a}_{m}-\mathbf{a}_{b}]_{\times}\delta\boldsymbol{\theta} -\mathbf{R}\delta \mathbf{a}_{b} + \delta \mathbf{g} - \mathbf{R}\mathbf{a}_{n}
\end{aligned} }
\end{equation}
식을 조금 더 다듬기 위해 가속도계의 노이즈가 white, uncorrelated, isotopic하다고 가정하면 다음 식이 성립한다.
\begin{equation}
\begin{aligned}
\mathbb{E}[\mathbf{a}_{n}] = 0 \quad \quad \mathbb{E}[\mathbf{a}_{n}\mathbf{a}_{n}^{\intercal}] = \sigma_{a}^{2} \mathbf{I}
\end{aligned}
\end{equation}
이는 공분산이 3차원 공간 상에서 구(sphere)의 형태를 지니며 구의 중심은 원점(origin)임을 의미한다. 그러므로 공분산 행렬은 회전에 대해 불변성을 지니게 된다. ($\mathbb{E}[\mathbf{R}\mathbf{a}_{n}] = \mathbf{R}\mathbb{E}[\mathbf{a}_{n}] = 0$ and $\mathbb{E}[(\mathbf{Ra}_{n})(\mathbf{Ra}_{n})^{\intercal}] = \mathbf{R}\mathbb{E}[\mathbf{a}_{n}\mathbf{a}_{n}^{\intercal}]\mathbf{R}^{\intercal} = \mathbf{R}\sigma^{2}_{a}\mathbf{I}\mathbf{R}^{\intercal} = \sigma^{2}_{a}\mathbf{I}$). 따라서 가속도 노이즈 벡터는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{a}_{n} \leftarrow \mathbf{R}\mathbf{a}_{n}
\end{aligned}
\end{equation}
따라서 최종적인 속도 에러 공식은 다음과 같다.
\begin{equation}
\boxed{
\begin{aligned}
\dot{\delta\mathbf{v}} = -\mathbf{R}[\mathbf{a}_{m}-\mathbf{a}_{b}]_{\times}\delta\boldsymbol{\theta} -\mathbf{R}\delta \mathbf{a}_{b} + \delta \mathbf{g} - \mathbf{a}_{n}
\end{aligned} }
\end{equation}
Equation (\ref{eq:57}): The orientation error 각도 에러 $\dot{\delta\boldsymbol{\theta}}$를 구하기 위해 다음과 같은 식으로부터 시작한다.
\begin{equation}
\begin{aligned}
& \dot{\mathbf{q}}_{t} = \frac{1}{2} \mathbf{q}_{t} \otimes \boldsymbol{\omega}_{t} \\
& \dot{\mathbf{q}} = \frac{1}{2} \mathbf{q} \otimes \boldsymbol{\omega} \\
\end{aligned}
\end{equation}
위 식은 true 상태와 nominal 상태에서 쿼터니언 공식이다. 앞서 속도 에러를 구했을 때와 마찬가지로 각속도를 두 개의 항으로 나눈다.
\begin{equation}
\begin{aligned}
& \boldsymbol{\omega} \triangleq \boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b} \\
& \delta \boldsymbol{\omega} \triangleq -\boldsymbol{\omega}_{b} - \boldsymbol{\omega}_{n} \\
\end{aligned} \label{eq:60}
\end{equation}
true 상태 각속도는 다음과 같이 nominal 파트와 error 파트로 나눌 수 있다.
\begin{equation}
\begin{aligned}
\boldsymbol{\omega}_{t} = \boldsymbol{\omega} + \delta \boldsymbol{\omega}
\end{aligned}
\end{equation}
위 식을 토대로 $\dot{\mathbf{q}}_{t}$를 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
(\dot{\mathbf{q} \otimes \delta \mathbf{q}}) & = \boxed { \dot{\mathbf{q}}_{t} } && = \frac{1}{2} \mathbf{q}_{t} \otimes \boldsymbol{\omega}_{t} \\
\dot{\mathbf{q}} \otimes \delta \mathbf{q} + \mathbf{q} \otimes \dot{\delta \mathbf{q}} & = && = \frac{1}{2}\mathbf{q} \otimes \delta \mathbf{q} \otimes \boldsymbol{\omega}_{t} \\
\frac{1}{2} \mathbf{q} \otimes \boldsymbol{\omega} \otimes \delta \mathbf{q} + \mathbf{q} \otimes \dot{\delta \mathbf{q}} & =
\end{aligned}
\end{equation}
이를 $\dot{\delta \mathbf{q}}$에 대해 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} 0 \\ \dot{\delta \boldsymbol{\theta}} \end{bmatrix} = \boxed { 2 \dot { \delta \mathbf{q}}} & = \delta \mathbf{q} \otimes \boldsymbol{\omega}_{t} - \boldsymbol{\omega} \otimes \delta \mathbf{q} \\
& = [\mathbf{q}]_{R}(\boldsymbol{\omega}_{t})\delta \mathbf{q} - [\mathbf{q}]_{L}(\boldsymbol{\omega})\delta \mathbf{q} \\
& = \begin{bmatrix} 0 & -(\boldsymbol{\omega}_{t} - \boldsymbol{\omega})^{\intercal} \\ (\boldsymbol{\omega} - \boldsymbol{\omega}) & -[\boldsymbol{\omega}_{t} + \boldsymbol{\omega}]_{\times} \end{bmatrix} \begin{bmatrix} 1 \\ \delta \boldsymbol{\theta}/2 \end{bmatrix} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2}) \\
& = \begin{bmatrix} 0 & -\delta \boldsymbol{\omega}^{\intercal} \\ \delta \boldsymbol{\omega} & -[2 \boldsymbol{\omega} + \delta \boldsymbol{\omega}]_{\times} \end{bmatrix} \begin{bmatrix} 1 \\ \delta \boldsymbol{\theta}/2 \end{bmatrix} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2})
\end{aligned}
\end{equation}
스칼라와 벡터 파트로 나누어서 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
& 0 = \delta \boldsymbol{\omega}^{\intercal} \delta \boldsymbol{\theta} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2}) \\
& \dot{\delta \boldsymbol{\theta}} = \delta \boldsymbol{\omega} - [\boldsymbol{\omega}]_{\times} \delta \boldsymbol{\theta} -\frac{1}{2} [\delta \boldsymbol{\omega}]_{\times} \delta \boldsymbol{\theta} + O (\left\| \delta \boldsymbol{\theta} \right \|^{2})
\end{aligned}
\end{equation}
위 첫번째 공식을 통해 $\delta \boldsymbol{\omega}^{\intercal} \delta \boldsymbol{\theta} = O(\left\| \delta \boldsymbol{\theta} \right\|^{2})$가 유도된다. 이는 2차항 이상의 고차항으로써 작은 값을 가지므로 실제로 큰 의미를 가지지는 않는다. 위 두번째 공식에서 고차항을 제거하고 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\dot{\delta \boldsymbol{\theta}} = -[\boldsymbol{\omega}]_{\times}\delta \boldsymbol{\theta} +\delta \boldsymbol{\omega}
\end{aligned}
\end{equation}
최종적으로 (\ref{eq:60})을 사용하여 위 식을 다시 표기하면 각도 에러에 대한 선형화 공식을 얻을 수 있다.
\begin{equation}
\begin{aligned}
\boxed{ \dot{\delta \boldsymbol{\theta}} = -[\boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b}]_{\times}\delta \boldsymbol{\theta} - \delta \boldsymbol{\omega}_{b} - \boldsymbol{\omega}_{n} }
\end{aligned}
\end{equation}
5.4 System kinematics in discrete time
이론과 달리 실제 IMU 센서 데이터는 샘플링 시간 $\Delta t > 0$ 간격으로 들어오는 이산 신호(discrete signal)이기 때문에 앞서 설명한 ESKF의 미분 방정식(differential equation)을 차분 방정식(difference equation)으로 이산 변환하는 작업이 필요하다. 이산 변환을 수행할 때 몇몇 식들은 closed-form solution이 존재하지만 몇몇 식들은 수치 적분이 필요한 경우가 존재한다. 차분 방정식의 다양한 수치해법 방법은 Appendix를 참조하면 된다. 해당 섹션에서는 Euler 수치 해법을 통해 식을 표현하였다.
이산 변환이 필요한 파트는 다음과 같다.
- nominal 상태 방정식
- error 상태 방정식 중
- The deterministic part: state dynamics and control
- The stocastic part: noise and perturbations
5.4.1 The nominal state kinematics
nominal 상태에 대한 차분 방정식은 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{p} \leftarrow \mathbf{p} + \mathbf{v} \Delta t + \frac{1}{2} (\mathbf{R}(\mathbf{a}_{m} - \mathbf{a}_{b})+\mathbf{g})\Delta t^{2} \\
& \mathbf{v} \leftarrow \mathbf{v} + (\mathbf{R}(\mathbf{a}_{m}-\mathbf{a}_{b}) + \mathbf{g}) \Delta t \\
& \mathbf{q} \leftarrow \mathbf{q} \otimes \mathbf{q}\{ \boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b} \Delta t \} \\
& \mathbf{a}_{b} \leftarrow \mathbf{a}_{b} \\
& \boldsymbol{\omega}_{b} \leftarrow \boldsymbol{\omega}_{b} \\
& \mathbf{g} \leftarrow \mathbf{g}
\end{aligned}
\end{equation}
위 식에서 $x \leftarrow f(x, \boldsymbol{\cdot})$의 의미는 시간에 따른 업데이트 $x_{k+1} = f(x_{k}, \boldsymbol{\cdot})$를 의미한다. $\mathbf{R} \triangleq \mathbf{R}\{\mathbf{q}\}$는 쿼터니언을 회전 행렬로 표기한 것을 의미하며 $\mathbf{q}\{v\}$는 angle-axis 벡터 $v$를 쿼터니언으로 변환한 것을 의미한다. 위 방식 외에도 다양한 수치 적분 방식들이 존재하는데 자세한 내용은 Appendix를 참조하면 된다.
5.4.2 The error-state kinematics
다음은 error 상태 방정식을 차분 방정식으로 변환해야 한다. error 상태 방정식 중 deterministic 파트는 일반 적분 공식과 동일하게 적분된다 (해당 파트가 Appendix C.2의 근사 공식을 따르는 경우에 해당). 이와 달리 stocastic 파트의 적분에는 random impluse 항이 추가된다. 자세한 내용은 Appendix E 파트를 참조하면 된다.
\begin{equation}
\begin{aligned}
& \delta \mathbf{p} \leftarrow \delta \mathbf{p} + \delta \mathbf{v} \Delta t \\
& \delta \mathbf{v} \leftarrow \delta \mathbf{v} + (-\mathbf{R}[\mathbf{a}_{m} - \mathbf{a}_{b}]_{\times}\delta \boldsymbol{\theta} -\mathbf{R}\delta \mathbf{a}_{b} + \delta \mathbf{g} )\Delta t + \mathbf{v}_{\mathbf{i}} \\
& \delta \boldsymbol{\theta} \leftarrow \mathbf{R}^{\intercal}\{(\boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b})\Delta t\}\delta \boldsymbol{\theta} - \delta \boldsymbol{\omega}_{b}\Delta t + \boldsymbol{\theta}_{\mathbf{i}} \\
& \delta \mathbf{a}_{b} \leftarrow \delta \mathbf{a}_{b} + \mathbf{a}_{\mathbf{i}} \\
& \delta \boldsymbol{\omega}_{b} \leftarrow \delta \boldsymbol{\omega}_{b} + \boldsymbol{\omega}_{\mathbf{i}} \\
& \delta \mathbf{g} \leftarrow \delta \mathbf{g}
\end{aligned}
\end{equation}
위 식 중 $\mathbf{v}_{\mathbf{i}}, \boldsymbol{\theta}_{\mathbf{i}}, \mathbf{a}_{\mathbf{i}}, \boldsymbol{\omega}_{\mathbf{i}}$는 각각 속도, 각도, 가속도 bias, 각속도 bias와 관련된 random impulse 항을 의미한다. 모든 random impluse 항은 white gaussian process로 모델링되었으며 평균은 0이다. 이들의 공분산 행렬은 $\mathbf{a}_{n}, \boldsymbol{\omega}_{n}, \mathbf{a}_{w}, \boldsymbol{\omega}_{\omega}$을 샘플링 시간 $\Delta t$에 대해 적분함으로써 구할 수 있다. 자세한 유도 과정은 Appendix E를 참조하면 된다.
\begin{equation}
\begin{aligned}
& \mathbf{V}_{\mathbf{i}} = \sigma^{2}_{\tilde{\mathbf{a}}_{n}} \Delta t^{2} \mathbf{I} \quad \quad [m^2/s^2] \\
& \Theta_{\mathbf{i}} = \sigma^{2}_{\tilde{\boldsymbol{\omega}}_{n}} \Delta t^{2} \mathbf{I} \quad \quad [rad^2]\\
& \mathbf{A}_{\mathbf{i}} = \sigma^{2}_{\mathbf{a}_{\omega}} \Delta t \mathbf{I} \quad \quad [m^2/s^4]\\
& \Omega_{\mathbf{i}} = \sigma^{2}_{\boldsymbol{\omega}_{\omega}} \Delta t \mathbf{I} \quad \quad [rad^2/s^2] \\
\end{aligned}
\end{equation}
위 식에서 $\sigma^{2}_{\tilde{\mathbf{a}}_{n}} [m/s^2], \sigma^{2}_{\tilde{\boldsymbol{\omega}}_{n}} [rad/s], \sigma^{2}_{\mathbf{a}_{\omega}} [m/s^2\sqrt{s}], \sigma^{2}_{\boldsymbol{\omega}_{\omega}}[rad/s\sqrt{s}]$ 항은 IMU datasheet에 주어진 값을 사용하거나 실험적으로 측정하여 사용한다.
5.4.3 The error-state Jacobian and perturbation matrices
해당 섹션에서는 error 차분 방정식의 자코비안을 구하는 방법에 대해 설명한다.
지금까지 설명한 공식을 컴팩트한 형태로 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{x} = \begin{bmatrix} \mathbf{p} \\ \mathbf{v} \\ \mathbf{q} \\ \mathbf{a}_{b} \\ \boldsymbol{\omega}_{b} \\ \mathbf{g} \end{bmatrix}, \quad \quad \delta \mathbf{x} = \begin{bmatrix} \delta \mathbf{p} \\ \delta \mathbf{v} \\ \delta \boldsymbol{\theta} \\ \delta \mathbf{a}_{b} \\ \delta \boldsymbol{\omega}_{b} \\ \delta \mathbf{g} \end{bmatrix} \quad \quad \mathbf{u}_{m} = \begin{bmatrix} \mathbf{a}_{m} \\ \boldsymbol{\omega}_{m} \end{bmatrix} \quad \quad \mathbf{i} = \begin{bmatrix} \mathbf{v}_{\mathbf{i}} \\ \boldsymbol{\theta}_{\mathbf{i}} \\ \mathbf{a}_{\mathbf{i}} \\ \boldsymbol{\omega}_{\mathbf{i}} \end{bmatrix}
\end{aligned}
\end{equation}
$\mathbf{x}$는 nominal 상태, $\delta \mathbf{x}$는 error 상태, $\mathbf{u}_{m}$은 IMU 센서 데이터, $\mathbf{i}$는 섭동 임펄스 벡터(perturbation impluses vector)를 의미한다.
이를 통해 에러 상태 시스템을 나타내면 다음과 같다.
\begin{equation}
\begin{aligned}
\delta \mathbf{x} \leftarrow f(\mathbf{x}, \delta \mathbf{x}, \mathbf{u}_{m}, \mathbf{i}) = \mathbf{F}_{\mathbf{x}} (\mathbf{x}, \mathbf{u}_{m}) \cdot \delta \mathbf{x} + \mathbf{F}_{\mathbf{i}} \cdot \mathbf{i}
\end{aligned}
\end{equation}
ESKF의 prediction 스텝은 다음과 같다.
\begin{equation}
\begin{aligned}
& \hat{\delta \mathbf{x}} \leftarrow \mathbf{F}_{\mathbf{x}} (\mathbf{x}, \mathbf{u}_{m})\cdot \hat{\delta \mathbf{x}} \\
& \mathbf{P} \leftarrow \mathbf{F}_{\mathbf{x}}\mathbf{P}\mathbf{F}_{\mathbf{x}}^{\intercal} + \mathbf{F}_{\mathbf{i}}\mathbf{Q}_{\mathbf{i}}\mathbf{F}_{\mathbf{i}}^{\intercal}
\end{aligned} \label{eq:61}
\end{equation}
위 식에서 $\delta \mathbf{x} \sim \mathcal{N}(\hat{\delta \mathbf{x}}, \mathbf{P})$이고 $\mathbf{F}_{\mathbf{x}}, \mathbf{F}_{\mathbf{i}}$는 $f()$ 함수의 에러와 섭동에 대한 자코비안을 의미한다. $\mathbf{Q}_{\mathbf{i}}$는 섭동 임펄스 벡터의 공분산 행렬을 의미한다. 자코비안을 자세하게 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{F}_{\mathbf{x}} = \left.\frac{\partial f}{\partial \delta \mathbf{x}}\right\vert_{\mathbf{x}, \mathbf{u}_{m}} = \begin{bmatrix}
\mathbf{I} & \mathbf{I}\Delta t & 0 & 0 & 0 & 0 \\
0 & \mathbf{I} & -\mathbf{R}[\mathbf{a}_{m}-\mathbf{a}_{b}]_{\times}\Delta t & -\mathbf{R}\Delta t & 0 & \mathbf{I}\Delta t \\
0 & 0 & \mathbf{R}^{\intercal}\{(\boldsymbol{\omega}_{m} - \boldsymbol{\omega}_{b})\Delta t \} & 0 & -\mathbf{I}\Delta t & 0 \\
0 & 0 & 0 & \mathbf{I} & 0 & 0 \\
0 & 0 & 0 & 0 & \mathbf{I} & 0 \\
0 & 0 & 0 & 0 & 0 & \mathbf{I}
\end{bmatrix}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{F}_{\mathbf{i}} = \left.\frac{\partial f}{\partial \delta \mathbf{i}}\right\vert_{\mathbf{x}, \mathbf{u}_{m}} = \begin{bmatrix}
0&0&0&0 \\
\mathbf{I} &0&0&0 \\
0&\mathbf{I}&0&0 \\
0&0&\mathbf{I}&0 \\
0&0&0&\mathbf{I} \\
0&0&0&0
\end{bmatrix} \quad \quad
\mathbf{Q}_{\mathbf{i}} = \begin{bmatrix}
\mathbf{V}_{\mathbf{i}} &0&0&0 \\
0& \Theta_{\mathbf{i}} &0&0 \\
0&0&\mathbf{A}_{\mathbf{i}} &0 \\
0&0&0& \Omega_{\mathbf{i}}
\end{bmatrix}
\end{aligned}
\end{equation}
위 식에서 자코비안 $\mathbf{F}_{\mathbf{x}}$은 시스템 천이행렬(system transition matrix)라고 불린다. 이는 어떤 수치 적분을 사용하느냐에 따라 형태가 달라지며 위 식은 미분방정식의 수치 해법 중 Euler 방법을 수행한 경우 자코비안을 의미한다. 보다 다양한 수치 해법에 대한 내용은 Appendix B,D를 참조하면 된다.
또한 $\delta \mathbf{x}$의 평균 $\hat{\delta \mathbf{x}}$은 0으로 초기화되어 시작하기 때문에 선형방정식인 (\ref{eq:61})의 첫번째 식은 항상 0이 된다. 따라서 실제 코드에서는 첫번째 식을 생략해도 되지만 코드로 구현할 때 헷갈림을 방지하기 위해 미리 구현해놓고 코멘트 처리해놓는 것을 추천한다.
(\ref{eq:61})의 두번째 공식은 반드시 사용해야 한다. 특히 $\mathbf{F}_{\mathbf{i}}\mathbf{Q}_{\mathbf{i}}\mathbf{F}_{\mathbf{i}}^{\intercal}$ 항은 시간이 지날수록 공분산 항이 증가하기 때문에 간과하지 않고 반드시 식에 포함해서 계산해야 한다.
6 Fusing IMU with complementary sensory data
IMU 센서를 보완할 수 있는 카메라 이미지 또는 GPS 데이터가 들어오게 되면, ESKF는 correction 스텝을 진행한다. 잘 디자인된 ESKF 시스템의 경우 IMU bias 값들이 관측 가능하고 정상적으로 이를 추정할 수 있어야 한다. 센서 조합은 다양하게 구성할 수 있으나 가장 일반적으로 사용하는 조합은 GPS + IMU, 단안카메라 + IMU 또는 스테레오 카메라 + IMU와 같이 구성하여 사용한다. 최근 몇 년 동안 카메라와 IMU를 퓨전하는 작업은 다양한 주목을 받아왔으며 활발한 연구가 진행되었다. 이러한 카메라 + IMU 조합은 GPS가 불가능한 지역 또는 스마트폰이나 UAV 같은 소형 디바이스에 사용하기 위해 주로 연구된다.
IMU 자체 센서 데이터는 ESKF의 prediction 스텝에 사용되었으나 IMU를 제외한 다른 센서 데이터는 correction 스텝에 사용되며 또한 IMU bias 에러 값을 관측 및 추정하는데 사용한다. correction 스텝은 다음과 같이 세 단계로 구성되어 있다.
- 칼만 필터링을 통해 error 상태 업데이트
- nominal 상태에 error 상태의 평균값을 적용
- error 상태 리셋
다음으로 위 세 단계를 각 섹션으로 다루어 설명한다.
6.1 Observation of the error state via filter correction
센서의 관측은 다음과 같은 방정식으로 표현할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{y} = h(\mathbf{x}_{t}) + v
\end{aligned}
\end{equation}
위 식에서 $h()$는 true 상태의 비선형 관측 함수이고 $v$는 공분산 $\mathbf{V}$의 white gaussian noise이다.
\begin{equation}
\begin{aligned}
v \sim \mathcal{N}(0, \mathbf{V})
\end{aligned}
\end{equation}
다음으로 error 상태를 추정하기 위한 ESKF의 correction 공식은 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{K} = \mathbf{PH}^{\intercal}(\mathbf{HPH}^{\intercal} + \mathbf{V})^{-1} \\
& \hat{\delta \mathbf{x}} \leftarrow \mathbf{K}(\mathbf{y} - h(\hat{\mathbf{x}}_{t})) \\
& \mathbf{P} \leftarrow (\mathbf{I} - \mathbf{KH})\mathbf{P}
\end{aligned}
\end{equation}
위 식에서 $\mathbf{H}$는 함수 $h()$의 $\delta \mathbf{x}$에 대한 자코비안을 의미하며 true 상태 $\hat{\mathbf{x}}_{t} = \mathbf{x} \oplus \hat{\delta \mathbf{x}}$ 일 때 측정(evaluated) 값을 의미한다. 그리고 prediction 스텝의 마지막 과정에서 error 상태는 0이 되므로 $\hat{\mathbf{x}}_{t} = \mathbf{x}$가 된다. 즉, $\mathbf{H}$는 nominal 에러 $\mathbf{x}$일 때 측정된 값을 가진다.
\begin{equation}
\begin{aligned}
\mathbf{H} \equiv \left.\frac{\partial h}{\partial \delta \mathbf{x}} \right\vert_{\mathbf{x}}
\end{aligned}
\end{equation}
6.1.1 Jacobian computation for the filter correction
앞서 설명한 자코비안 $\mathbf{H}$는 다양한 방법으로 계산할 수 있다. 가장 자주 사용되는 방법 중 하나는 연쇄 법칙(chain rule)을 사용하는 것이다.
\begin{equation}
\begin{aligned}
\mathbf{H} \triangleq \left.\frac{\partial h}{\partial \delta \mathbf{x}} \right\vert_{\mathbf{x}} = \left.\frac{\partial h}{\partial \mathbf{x}_{t}} \right\vert_{\mathbf{x}} \left.\frac{\partial \mathbf{x}_{t}}{\partial \delta \mathbf{x}} \right\vert_{\mathbf{x}} = \mathbf{H}_{\mathbf{x}} \mathbf{X}_{\delta \mathbf{x}}
\end{aligned}
\end{equation}
이 때, $\mathbf{H}_{\mathbf{x}} \triangleq \left.\frac{\partial h}{\partial \mathbf{x}_{t}}\right\vert_{\mathbf{x}}$는 EKF에서 사용하는 자코비안과 동일하다. 위 연쇄 법칙 중 첫번째 부분이 특정 센서를 사용했을 때 관측 함수와 연관되어 있다.
두번째 부분인 $\mathbf{X}_{\delta \mathbf{x}} \triangleq \left.\frac{\partial \mathbf{x}_{t}}{\partial \delta \mathbf{x}}\right\vert_{\mathbf{x}}$는 true 상태의 error 상태에 대한 자코비안을 의미한다. 해당 파트는 ESKF의 합성(composition) 공식을 통해 유도가 가능하다.
\begin{equation}
\begin{aligned}
\mathbf{X}_{\delta \mathbf{x}} = \begin{bmatrix}
\frac{\partial \mathbf{p}+\delta \mathbf{p}}{\partial \delta \mathbf{p}} &&&&& \\
& \frac{\partial \mathbf{v}+\delta \mathbf{v}}{\partial \delta \mathbf{v}} &&&& \\
& & \frac{\partial \mathbf{q} \otimes \delta \mathbf{q}}{\partial \delta \boldsymbol{\theta}} &&& \\
& & & \frac{\partial \mathbf{a}_{b} + \delta \mathbf{a}_{b}}{\partial \delta \mathbf{a}_{b}} && \\
& & & & \frac{\partial \boldsymbol{\omega}_{b} + \delta \boldsymbol{\omega}_{b}}{\partial \delta \boldsymbol{\omega}_{b}} & \\
& & & & & \frac{\partial \mathbf{g} + \delta \mathbf{g}}{\partial \delta \mathbf{g}} \\
\end{bmatrix}
\end{aligned}
\end{equation}
위 행렬은 $\mathbf{Q}_{\delta \boldsymbol{\theta}} = \partial(\mathbf{q}\otimes \mathbf{q}) / \partial \delta \boldsymbol{\theta}$의 4x3 행렬 값을 제외하고 모두 3x3 항등 행렬($\mathbf{I}_{3}$) 값을 가진다. (e.g., $\frac{\partial \mathbf{p}+\delta \mathbf{p}}{\partial \delta \mathbf{p}} = \mathbf{I}_{3}$). 따라서 이를 컴팩트하게 나타내면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{X}_{\delta \mathbf{x}} \triangleq \left.\frac{\partial \mathbf{x}_{t}}{\partial \delta \mathbf{x}}\right\vert_{\mathbf{x}} = \begin{bmatrix}
\mathbf{I}_{6} &0&0 \\
0 & \mathbf{Q}_{\delta \boldsymbol{\theta}} & 0 \\
0&0& \mathbf{I}_{9}
\end{bmatrix}
\end{aligned}
\end{equation}
충분히 작은 쿼터니언 값은 (\ref{eq:64})에 따라 $\delta \mathbf{q} \rightarrow_{(\delta \boldsymbol{\theta} \rightarrow 0)} \begin{bmatrix} 1 \\ \frac{1}{2}\delta \boldsymbol{\theta} \end{bmatrix}$ 같이 근사될 수 있으므로 이를 사용하여 $\mathbf{Q}_{\delta \boldsymbol{\theta}}$를 다시 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{Q}_{\delta \boldsymbol{\theta}} \triangleq \left.\frac{\partial(\mathbf{q}\otimes \delta \mathbf{q})}{\partial \delta \boldsymbol{\theta}}\right\vert_{\mathbf{q}} & = \left.\frac{\partial(\mathbf{q}\otimes \delta \mathbf{q})}{\partial \delta \mathbf{q}}\right\vert_{\mathbf{q}} \left. \frac{\partial \delta \mathbf{q}}{\partial \delta \boldsymbol{\theta}} \right\vert_{\mathbf{\delta \boldsymbol{\theta}}=0} \\
& = \left.\frac{\partial([\mathbf{q}]_{L} \delta \mathbf{q})}{\partial \delta \mathbf{q}}\right\vert_{\mathbf{q}} \left. \frac{\partial \begin{bmatrix} 1 \\ \frac{1}{2}\partial \boldsymbol{\theta} \end{bmatrix}}{\partial \delta \boldsymbol{\theta}} \right\vert_{\delta \boldsymbol{\theta}=0} \\
& = [\mathbf{q}]_{L}\frac{1}{2} \begin{bmatrix} 0&0&0 \\ 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix}
\end{aligned}
\end{equation}
이를 정리하면 최종적으로 다음과 같은 공식을 얻을 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{Q}_{\delta \boldsymbol{\theta}} = \frac{1}{2} \begin{bmatrix} -q_{x} &-q_{y} & -q_{z} \\ q_{w} & -q_{z} & q_{y} \\ q_{z} & q_{w} & -q_{x} \\ -q_{y} & q_{x} & q_{w} \end{bmatrix}
\end{aligned}
\end{equation}
6.2 Injection of the observed error into the nominal state
이전 단계를 수행하여 ESKF 값이 업데이트가 되면 nominal 상태 값에 업데이트된 error 상태값이 적용된다.
\begin{equation}
\begin{aligned}
\mathbf{x} \leftarrow \mathbf{x} \oplus \hat{\delta \mathbf{x}}
\end{aligned}
\end{equation}
이를 풀어쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{p} \leftarrow \mathbf{p} + \hat{\delta \mathbf{p}} \\
& \mathbf{v} \leftarrow \mathbf{v} + \hat{\delta \mathbf{v}} \\
& \mathbf{q} \leftarrow \mathbf{q} \otimes \mathbf{q}\{\hat{\delta \boldsymbol{\theta}}\} \\
& \mathbf{a}_{b} \leftarrow \mathbf{a}_{b} + \hat{\delta \mathbf{a}_{b}} \\
& \boldsymbol{\omega}_{b} \leftarrow \boldsymbol{\omega}_{b} + \hat{\delta \boldsymbol{\omega}_{b}} \\
& \mathbf{g} \leftarrow \mathbf{g} +\hat{\delta \mathbf{g}}
\end{aligned}
\end{equation}
6.3 ESKF reset
nominal 상태가 정상적으로 업데이트되면 다음으로 error 상태의 평균값 $\hat{\delta \mathbf{x}}$을 리셋한다. 리셋을 하는 이유는 새로운 nominal 상태의 방향 프레임(orientation frame)에 대한 지역적(locally)인 새로운 방향 에러(new orientation error)를 표현해야 하기 때문이다. ESKF 업데이트의 최종 단계에서는 이러한 새로운 방향 에러를 기반으로 error 상태의 공분산 $\mathbf{P}$이 업데이트된다.
error 리셋 함수를 $g()$라고 하면 이는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\delta \mathbf{x} \leftarrow g(\delta \mathbf{x}) = \delta \mathbf{x} \ominus \hat{\delta \mathbf{x}}
\end{aligned}
\end{equation}
여기서 $\ominus$는 합성(composition)의 역연산을 의미한다. ESKF의 리셋 과정은 다음과 같다.
\begin{equation}
\begin{aligned}
& \hat{\delta \mathbf{x}} \leftarrow 0 \\
& \mathbf{P} \leftarrow \mathbf{GPG}^{\intercal}
\end{aligned}
\end{equation}
$\mathbf{G}$는 다음과 같이 정의된 자코비안을 의미한다.
\begin{equation}
\begin{aligned}
\mathbf{G} \triangleq \left. \frac{\partial g}{\partial \delta \mathbf{x}}\right\vert_{\hat{\delta \mathbf{x}}}
\end{aligned}
\end{equation}
앞서 설명했던 다른 자코비안들과 동일하게 $\mathbf{G}$도 방향 에러를 제외하고 모든 부분은 항등 행렬($\mathbf{I}$)를 가진다. 방향 에러 $\partial \delta \boldsymbol{\theta}^{+} / \partial \delta \boldsymbol{\theta} = \mathbf{I} - [\frac{1}{2}\hat{\delta \boldsymbol{\theta}}]_{\times}$는 다음 섹션에서 자세히 유도한다. 자코비안 $\mathbf{G}$을 풀어서 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{G} = \begin{bmatrix} \mathbf{I}_{6} &0&0 \\ 0 & \mathbf{I} - [\frac{1}{2}\hat{\delta \boldsymbol{\theta}}]_{\times} & 0 \\ 0&0& \mathbf{I}_{9} \end{bmatrix}
\end{aligned}
\end{equation}
대부분의 구현된 ESKF 코드들은 에러항 $\hat{\delta \boldsymbol{\theta}}$ 값을 무시하여 $\mathbf{G} = \mathbf{I}_{18}$과 같이 단순하게 표현하여 사용한다. 필자는 위 자코비안을 근사한 값이 아닌 정확한 값을 표기하였으며 독자들 중 장기간 odometry를 추정할 때 생기는 드리프트와 같은 에러를 디버깅할 때 해당 행렬을 참조하면 좋을 것이라고 생각한다.
6.3.1 Jacobian of the reset operation with respect to the orientation error
새로운 nominal 상태의 방향 에러를 $\delta \boldsymbol{\theta}^{+}$라고 하고 기존의 에러를 $\delta \boldsymbol{\theta}$, 업데이트된 에러의 평균값을 $\hat{\delta \boldsymbol{\theta}}$라고 하자. 이를 사용하여 다음과 같은 사실을 알 수 있다.
- true 방향 값은 error가 리셋될 때 변하지 않는다. i.e., $\mathbf{q}^{+}_{t} = \mathbf{q}_{t}$이다.
\begin{equation}
\begin{aligned}
\mathbf{q}^{+} \otimes \delta \mathbf{q}^{+} = \mathbf{q} \otimes \delta \mathbf{q}
\end{aligned}
\end{equation} - 업데이트된 에러의 평균값은 nominal 상태에 적용된다.
\begin{equation}
\begin{aligned}
\mathbf{q}^{+} = \mathbf{q} \otimes \hat{\delta \mathbf{q}}
\end{aligned}
\end{equation}
위 두 사실을 결합하여 $\delta \mathbf{q}^{+}$를 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\delta \mathbf{q}^{+} = (\mathbf{q}^{+})^{*} \otimes \mathbf{q} \otimes \delta \mathbf{q} = (\mathbf{q} \otimes \hat{\delta \mathbf{q}})^{*} \otimes \mathbf{q} \otimes \delta \mathbf{q} = \hat{\delta \mathbf{q}}^{*} \otimes \delta \mathbf{q} = [\hat{\delta \mathbf{q}}]_{L} \cdot \delta \mathbf{q}
\end{aligned}
\end{equation}
(\ref{eq:64})에 따라 충분히 작은 쿼터니언은 $\hat{\delta \mathbf{q}}^{*} \approx \begin{bmatrix} 1 \\ -\frac{1}{2} \hat{\delta \boldsymbol{\theta}} \end{bmatrix}$와 같이 나타낼 수 있으므로 위 식은 다음과 같이 전개된다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} 1 \\ \frac{1}{2}\delta \boldsymbol{\theta}^{+} \end{bmatrix} = \begin{bmatrix} 1 & \frac{1}{2}\hat{\delta \boldsymbol{\theta}}^{\intercal} \\ -\frac{1}{2} \hat{\delta \boldsymbol{\theta}} & \mathbf{I} - [\frac{1}{2}\hat{\delta \boldsymbol{\theta}}]_{\times} \end{bmatrix} \cdot \begin{bmatrix} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta} \end{bmatrix} + O(\left\| \delta \boldsymbol{\theta}\right\|^{2})
\end{aligned}
\end{equation}
위 식은 하나의 스칼라와 하나의 벡터 식으로 분리할 수 있다.
\begin{equation}
\begin{aligned}
& \frac{1}{4} \hat{\delta \boldsymbol{\theta}}^{\intercal} \delta \boldsymbol{\theta} = O(\left\| \delta \boldsymbol{\theta} \right\|^{2}) \\
& \delta \boldsymbol{\theta}^{+} = -\hat{\delta \boldsymbol{\theta}} + \bigg(\mathbf{I} - \bigg[\frac{1}{2}\hat{\delta \boldsymbol{\theta}} \bigg]_{\times} \bigg) \delta \boldsymbol{\theta} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2})
\end{aligned}
\end{equation}
위 첫번째 식은 고차항의 관련된 식이므로 크게 중요하지 않은 식이다. 하지만 위 두번째 식은 $\hat{\delta \boldsymbol{\theta}}^{+} = 0$ 일 때 리셋 연산을 의미하므로 중요한 식이다. 이를 통해 자코비안을 쉽게 구할 수 있다.
\begin{equation}
\begin{aligned}
\boxed{ \frac{\partial \delta \boldsymbol{\theta}^{+}}{\partial \delta \boldsymbol{\theta}} = \mathbf{I} - \bigg[\frac{1}{2} \hat{\delta \boldsymbol{\theta}} \bigg]_{\times} }
\end{aligned}
\end{equation}
7 The ESKF using global angular errors
이전 섹션에서 각 에러(angular error)를 지역(local) 좌표계에서 정의하였던 것과 달리 해당 섹션에서는 각 에러를 전역(global) 좌표계에서 정의하여 에러 상태 방정식을 표현하는 것에 대해 설명한다. 전역 좌표계에서 정의된 각 에러 $\delta \boldsymbol{\theta}$는 왼쪽 방향에서 합성 연산을 하는 것으로 표현할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{q}_{t} = \delta \mathbf{q} \otimes \mathbf{q} = \mathbf{q} \{ \delta \boldsymbol{\theta}\} \otimes \mathbf{q}
\end{aligned}
\end{equation}
각 에러와 달리 각속도 벡터 $\boldsymbol{\omega}$는 지역적으로 정의된 표현을 그대로 사용한다. 즉, 연속 시간의 경우 $\dot{\mathbf{q}} = \frac{1}{2} \mathbf{q} \otimes \boldsymbol{\omega}$를 만족하고 이산 시간의 경우 $\mathbf{q} \leftarrow \mathbf{q} \otimes \mathbf{q}\{ \boldsymbol{\omega}\Delta t\}$를 만족한다. 이는 IMU 센서에서 나오는 각속도 벡터를 변환없이 그대로 사용해도 되기 때문에 편리한 이점을 지닌다.
7.1 System kinematics in continuous time
7.1.1 The true-and nominal-state kinematics
true, nominal 상태는 에러를 포함하고 있지 않으므로 지역 좌표계와 동일한 수식을 가진다.
7.1.2 The error-state kinematics
각 에러 $\delta \boldsymbol{\theta}$가 전역 좌표계에서 정의된 경우 error 상태 방정식은 다음과 같다. 우선 수식을 먼저 소개한 후 이후에 유도 과정에 대해 설명한다.
\begin{equation}
\begin{aligned}
& \dot{\delta \mathbf{p}} = \delta \mathbf{v} \\
& \dot{\delta \mathbf{v}} = -[\mathbf{R}(\mathbf{a}_{m} -b \mathbf{a}_{b})]_{\times} \delta \boldsymbol{\theta} - \mathbf{R} \delta \mathbf{a}_{b} + \delta \mathbf{g} - \mathbf{R}\mathbf{a}_{n} \\
& \dot{\delta \boldsymbol{\theta}} = -\mathbf{R}\delta \boldsymbol{\omega}_{b} - \mathbf{R}\boldsymbol{\omega}_{n} \\
& \dot{\delta \mathbf{a}_{b}} = \mathbf{a}_{\omega} \\
& \dot{\delta \boldsymbol{\omega}_{b}} = \boldsymbol{\omega}_{\omega} \\
& \dot{\delta \mathbf{g}} = 0
\end{aligned}
\label{eq:100}
\end{equation}
지역 좌표계에서 정의되었을 때와 동일하게 $\dot{\delta \mathbf{v}}$, $\dot{\delta \boldsymbol{\theta}}$를 제외한 식들은 자명하다. 자명하지 않은 두 상태 방정식을 유도하는 과정은 다음과 같다.
Equation (\ref{eq:100}): The linear velocity error: $\dot{\delta \mathbf{v}}$를 유도하기 위해 아래 방정식으로부터 시작한다.
\begin{equation}
\begin{aligned}
& \mathbf{R}_{t} = (\mathbf{I} + [\delta \boldsymbol{\theta}]_{\times})\mathbf{R} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2}) \\
& \dot{\mathbf{v}} = \mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{g}
\end{aligned}
\end{equation}
$\mathbf{R}_{t}$ 식은 회전량이 작을 때 이를 근사하는 식을 의미하며 이 때 각 에러 $\delta \boldsymbol{\theta}$는 전역 좌표계에서 정의된 각 에러를 의미한다. $\dot{\mathbf{v}}$ 식은 nominal 상태의 $\dot{\mathbf{v}}$ 식을 $\mathbf{a}_{\mathcal{B}}$와 $\delta \mathbf{a}_{\mathcal{B}}$를 통해 나타낸 식이다. $\mathbf{a}_{\mathcal{B}}$와 $\delta \mathbf{a}_{\mathcal{B}}$는 앞서 챕터 5에서 정의했던 식 (\ref{eq:58})과 동일하다.
이를 통해 (\ref{eq:56})에서 정의한 $\dot{\mathbf{v}}_{t}$ 식을 좌우로 전개하면 다음과 같다. 이 때, 2차항 이상의 고차항 $O(\left\| \delta \boldsymbol{\theta} \right\|^{2})$는 작은 값이므로 무시한다.
\begin{equation}
\begin{aligned}
\dot{\mathbf{v}} + \dot{ \delta \mathbf{v}} & = \boxed{ \dot{\mathbf{v}}_{t} } && = (\mathbf{I} + [\delta \boldsymbol{\theta}]_{\times})\mathbf{R}(\mathbf{a}_{\mathcal{B}} + \delta \mathbf{a}_{\mathcal{B}}) + \mathbf{g} + \delta \mathbf{g} \\
\mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{g} + \dot{\delta \mathbf{v}} & = && = \mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{R}\delta \mathbf{a}_{\mathcal{B}} + [\delta \boldsymbol{\theta}]_{\times} \mathbf{R}\mathbf{a}_{\mathcal{B}} + [\delta \boldsymbol{\theta}]_{\times} \mathbf{R} \delta \mathbf{a}_{\mathcal{B}} + \mathbf{g} + \delta \mathbf{g}
\end{aligned}
\end{equation}
양 변의 $\mathbf{R}\mathbf{a}_{\mathcal{B}} + \mathbf{g}$를 제거한 후 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\dot{\delta \mathbf{v}} = \mathbf{R}\delta \mathbf{a}_{\mathcal{B}} + [\delta \boldsymbol{\theta}]_{\times} \mathbf{R}(\mathbf{a}_{\mathcal{B}} + \delta \mathbf{a}_{\mathcal{B}}) + \delta \mathbf{g}
\end{aligned}
\end{equation}
고차항 값들을 제거하고 $[\mathbf{a}]_{\times}\mathbf{b} = -[\mathbf{b}]_{\times}\mathbf{a}$ 성질을 사용하여 식을 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\dot{\delta \mathbf{v}} = \mathbf{R}\delta \mathbf{a}_{\mathcal{B}} - [\mathbf{R}\mathbf{a}_{\mathcal{B}}]_{\times} \delta \boldsymbol{\theta} + \delta \mathbf{g}
\end{aligned}
\end{equation}
최종적으로 (\ref{eq:58})을 사용하여 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\boxed{ \dot{\delta \mathbf{v}} = -[\mathbf{R}(\mathbf{a}_{m} - \mathbf{a}_{b})]_{\times} \delta \boldsymbol{\theta} - \mathbf{R}\mathbf{a}_{b} +\delta \mathbf{g} - \mathbf{Ra}_{n} }
\end{aligned}
\end{equation}
Equation (\ref{eq:100}): The orientation error: 각도 에러를 구하기 위해서 쿼터니언의 true, nominal 상태의 미분 방정식으로부터 시작한다.
\begin{equation}
\begin{aligned}
& \dot{\mathbf{q}}_{t} = \frac{1}{2}\mathbf{q}_{t} \otimes \boldsymbol{\omega}_{t}\\
& \dot{\mathbf{q}} = \frac{1}{2}\mathbf{q} \otimes \boldsymbol{\omega}
\end{aligned}
\end{equation}
이 때 사용한 쿼터니언은 전역 좌표계에서 정의된 쿼터니언을 의미한다.
\begin{equation}
\begin{aligned}
\mathbf{q}_{t} = \delta \mathbf{q} \otimes \mathbf{q}
\end{aligned}
\end{equation}
(\ref{eq:60})과 같이 지역 좌표계에서 유도할 때와 동일하게 각속도를 큰 값과 작은 값으로 나눈다. 그리고 좌우로 전개하여 전개해보면 다음과 같다.
\begin{equation}
\begin{aligned}
(\dot{\delta \mathbf{q} \otimes \mathbf{q}}) & = \boxed{ \dot{\mathbf{q}}_{t} } && = \frac{1}{2}\mathbf{q}_{t} \otimes \boldsymbol{\omega}_{t} \\
\dot{\delta \mathbf{q}} \otimes \mathbf{q} + \delta \mathbf{q} \otimes \dot{\mathbf{q}} & = && = \frac{1}{2}\delta \mathbf{q} \otimes \mathbf{q} \otimes \boldsymbol{\omega}_{t} \\
\dot{\delta \mathbf{q}} \otimes \mathbf{q} + \frac{1}{2}\delta \mathbf{q} \otimes \mathbf{q} \otimes \boldsymbol{\omega} & =
\end{aligned}
\end{equation}
$\boldsymbol{\omega}_{t} = \boldsymbol{\omega} +\delta \boldsymbol{\omega}$를 활용하여 위 식은 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\dot{\delta \mathbf{q}} \otimes \mathbf{q} = \frac{1}{2} \delta \mathbf{q} \otimes \mathbf{q} \otimes \delta \boldsymbol{\omega}
\end{aligned}
\end{equation}
양변에 $\mathbf{q}^{*}$를 곱해주고 $\mathbf{q}\otimes \delta \boldsymbol{\omega} \otimes \mathbf{q}^{*} = \mathbf{R}\delta \boldsymbol{\omega}$를 활용하여 다음과 같이 식을 정리할 수 있다.
\begin{equation}
\begin{aligned}
\dot{\delta \mathbf{q}} & = \frac{1}{2} \delta \mathbf{q} \otimes \mathbf{q} \otimes \delta \boldsymbol{\omega} \otimes \mathbf{q}^{*} \\
& = \frac{1}{2}\delta \mathbf{q} \otimes (\mathbf{R}\delta \boldsymbol{\omega}) \\
& = \frac{1}{2}\delta \mathbf{q} \otimes \delta \boldsymbol{\omega}_{G}
\end{aligned}
\end{equation}
이 때, $\delta \boldsymbol{\omega}_{G} \triangleq \mathbf{R}\delta \boldsymbol{\omega}$는 전역 좌표계에서 정의된 작은 각속도를 의미한다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} 0 \\ \dot{\delta \boldsymbol{\theta}} \end{bmatrix} = \boxed{ 2\dot{\delta \mathbf{q}}} & = \delta \mathbf{q} \otimes \delta \boldsymbol{\omega}_{G} \\
& = \Omega(\delta \boldsymbol{\omega}_{G}) \delta \mathbf{q} \\
& = \begin{bmatrix} 0 & -\delta \boldsymbol{\omega}_{G}^{\intercal} \\ \delta \boldsymbol{\omega}_{G} & -[\delta \boldsymbol{\omega}_{G}]_{\times} \end{bmatrix} \begin{bmatrix} 1 \\ \delta \boldsymbol{\theta}/2 \end{bmatrix} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2}
)
\end{aligned}
\end{equation}
위 식을 스칼라와 벡터 파트로 나누면 다음과 같다.
\begin{equation}
\begin{aligned}
& 0 = \delta \boldsymbol{\omega}^{\intercal}_{G} \delta \boldsymbol{\theta} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2}) \\
& \dot{\delta \boldsymbol{\theta}} = \delta \boldsymbol{\omega}_{G} - \frac{1}{2}[\delta \boldsymbol{\omega}_{G}]_{\times} \delta \boldsymbol{\theta} + O(\left\| \delta \boldsymbol{\theta} \right\|^{2})
\end{aligned}
\end{equation}
위 첫번째 식을 통해 $\delta \boldsymbol{\omega}_{G}^{\intercal} \delta \boldsymbol{\theta} = O(\left\| \delta \boldsymbol{\theta} \right\|^{2})$를 얻을 수 있다. 이는 2차항 이상의 고차항으로써 작은 값을 가지므로 실제로 큰 의미를 가지지는 않는다. 위 두번째 공식에서 고차항을 제거하고 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\dot{\delta \boldsymbol{\theta}} = -[\boldsymbol{\omega}]_{\times} \delta \boldsymbol{\theta} + \delta \boldsymbol{\omega}
\end{aligned}
\end{equation}
최종적으로 (\ref{eq:60})을 사용하여 위 식을 다시 표기하면 각도 에러에 대한 선형화 공식을 얻을 수 있다.
\begin{equation}
\begin{aligned}
\boxed{ \dot{\delta \boldsymbol{\theta}} = -\mathbf{R}\delta \boldsymbol{\omega}_{b} - \mathbf{R}\boldsymbol{\omega}_{n}}
\end{aligned}
\end{equation}
7.2 System kinematics in discrete time
7.2.1 The nominal state
nominal 상태는 에러 값을 포함하지 않으므로 지역 좌표계에서 표기한 식과 동일하다.
7.2.2 The error state
Euler 수치 해법을 사용하여 error 상태 방정식을 차분 방정식으로 표기하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \delta \mathbf{p} \leftarrow \delta \mathbf{p} + \delta \mathbf{v} \Delta t \\
& \delta \mathbf{v} \leftarrow \delta \mathbf{v} + (-\mathbf{R}[\mathbf{a}_{m} - \mathbf{a}_{b}]_{\times}\delta \boldsymbol{\theta} -\mathbf{R}\delta \mathbf{a}_{b} + \delta \mathbf{g} )\Delta t + \mathbf{v}_{\mathbf{i}} \\
& \delta \boldsymbol{\theta} \leftarrow \delta \boldsymbol{\theta} - \mathbf{R}\delta \boldsymbol{\omega}_{b} \Delta t + \boldsymbol{\theta}_{\mathbf{i}} \\
& \delta \mathbf{a}_{b} \leftarrow \delta \mathbf{a}_{b} + \mathbf{a}_{\mathbf{i}} \\
& \delta \boldsymbol{\omega}_{b} \leftarrow \delta \boldsymbol{\omega}_{b} + \boldsymbol{\omega}_{\mathbf{i}} \\
& \delta \mathbf{g} \leftarrow \delta \mathbf{g}
\end{aligned}
\end{equation}
위 방정식은 $\delta \boldsymbol{\theta}$를 제외하고는 지역 좌표계에서 표기한 식과 동일하다.
7.2.3 The error state Jacobian and pertubation matrices
전역 좌표계일 때 상태 천이행렬 $\mathbf{F}_{\mathbf{x}}$는 앞서 설명한 error 상태 방정식으로부터 얻을 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{F}_{\mathbf{x}} = \begin{bmatrix} \mathbf{I} & \mathbf{I}\Delta t & 0&0&0&0 \\
0 & \mathbf{I} & \boxed{ -[\mathbf{R}(\mathbf{a}_{m}-\mathbf{a}_{b})]_{\times}\Delta t} & -\mathbf{R}\Delta t & 0 & \mathbf{I}\Delta t \\
0&0& \boxed{\mathbf{I}} &0 & \boxed{-\mathbf{R}\Delta t} & 0 \\
0 &0&0& \mathbf{I}&0&0 \\
0&0&0&0&\mathbf{I}&0 \\
0&0&0&0&0&\mathbf{I}
\end{bmatrix}
\end{aligned}
\end{equation}
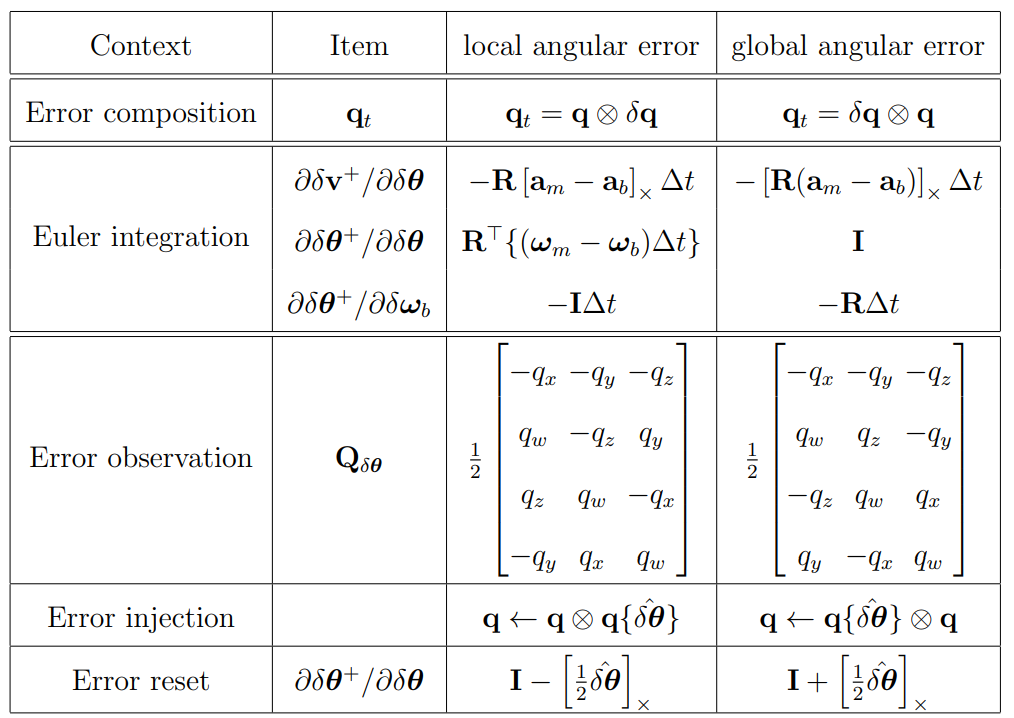
지역 좌표계의 $\mathbf{F}_{\mathbf{x}}$와 다른 부분은 박스로 표기하였다. 자세한 변경 사항은 테이블 \ref{fig:10}에 정리하였다.
섭동 자코비안(perturbation jacobian)과 섭동 행렬은 지역 좌표계에서 사용했던 행렬과 동일하다.
\begin{equation}
\begin{aligned}
\mathbf{F}_{\mathbf{i}}= \begin{bmatrix}
0&0&0&0 \\
\mathbf{I}&0&0&0 \\
0&\mathbf{I}&0&0 \\
0&0&\mathbf{I}&0 \\
0&0&0&\mathbf{I} \\
0&0&0&0 \\
\end{bmatrix} \quad \quad
\mathbf{Q}_{\mathbf{i}} = \begin{bmatrix}
\mathbf{V}_{\mathbf{i}} &0&0&0 \\
0&\Theta_{\mathbf{i}}&0&0 \\
0&0&\mathbf{A}_{\mathbf{i}}&0 \\
0&0&0&\Omega_{\mathbf{i}}
\end{bmatrix}
\end{aligned}
\end{equation}
7.3 Fusing with complementary sensory data
IMU 이외의 센서를 퓨전하여 ESKF correction 스텝을 진행하는 과정은 전역 각 에러(global angular error) 부분만 변경되었다. 따라서 모든 correction 스텝에서 전역 각 에러 부분만 변경해주면 된다.
7.3.1 Error state observation
지역 좌표계에서 소개했던 자코비안 행렬의 블록 중에서 전역 각 에러에 대한 부분만 변경해주면 된다. 작은 쿼터니언 값에 대한 1차 테일러 근사 $\delta \mathbf{q} \rightarrow \begin{bmatrix} 1 \\ \frac{1}{2}\delta \boldsymbol{\theta} \end{bmatrix}$를 활용하여 $\mathbf{Q}_{\delta \boldsymbol{\theta}}$를 나타내면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{Q}_{\delta \boldsymbol{\theta}} \triangleq \left. \frac{\partial (\delta \mathbf{q} \otimes \mathbf{q})}{\partial \delta \boldsymbol{\theta}} \right\vert_{\mathbf{q}} & = \left. \frac{\partial (\delta \mathbf{q} \otimes \mathbf{q})}{\partial \delta \mathbf{q}} \right\vert_{\mathbf{q}} \left. \frac{\partial \delta \mathbf{q}}{\partial \delta \boldsymbol{\theta}} \right\vert_{\hat{\delta \boldsymbol{\theta}} = 0} \\
& = [\mathbf{q}]_{R}\frac{1}{2} \begin{bmatrix} 0&0&0 \\ 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix} \\
& = \frac{1}{2} \begin{bmatrix} -q_x & -q_y & -q_z \\ q_w & q_{z} & -q_{y} \\
-q_{z} &q_{w} & q_{x} \\ q_{y} & -q_x & q_{w}
\end{bmatrix}
\end{aligned}
\end{equation}
위 식은 지역 좌표계의 $\mathbf{Q}_{\delta \boldsymbol{\theta}} = [\mathbf{q}]_{L}\frac{1}{2} \begin{bmatrix} 0&0&0 \\ 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix}$과 $[\mathbf{q}]_{L} \leftrightarrow [\mathbf{q}]_{R}$ 부분이 다른 것을 확인할 수 있다.
7.3.2 Injection of the observed error into the nominal state
이전 단계를 수행하여 ESKF 값이 업데이트가 되면 $\mathbf{x} \leftarrow \mathbf{x} \oplus \hat{\delta \mathbf{x}}$와 같이 nominal 상태 값에 업데이트된 error 상태값이 적용된다.
\begin{equation}
\begin{aligned}
& \mathbf{p} \leftarrow \mathbf{p} + \hat{\delta \mathbf{p}} \\
& \mathbf{v} \leftarrow \mathbf{v} + \hat{\delta \mathbf{v}} \\
& \mathbf{q} \leftarrow \mathbf{q}\{\hat{\delta \boldsymbol{\theta}}\} \otimes \mathbf{q} \\
& \mathbf{a}_{b} \leftarrow \mathbf{a}_{b} + \hat{\delta \mathbf{a}_{b}} \\
& \boldsymbol{\omega}_{b} \leftarrow \boldsymbol{\omega}_{b} + \hat{\delta \boldsymbol{\omega}_{b}} \\
& \mathbf{g} \leftarrow \mathbf{g} +\hat{\delta \mathbf{g}}
\end{aligned}
\end{equation}
위 식은 지역 좌표계의 업데이트 식에서 쿼터니언 부분만 변경되었다. 모든 변경사항은 테이블 \ref{fig:10}에 요약하였다.
7.3.3 ESKF reset
nominal 상태가 정상적으로 업데이트되면 다음으로 error 상태의 평균값 $\hat{\delta \mathbf{x}}$을 리셋한다.
\begin{equation}
\begin{aligned}
& \hat{\delta \mathbf{x}} \leftarrow 0 \\
& \mathbf{P} \leftarrow \mathbf{GPG}^{\intercal}
\end{aligned}
\end{equation}
자코비안 $\mathbf{G}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{G} = \begin{bmatrix} \mathbf{I}_{6} & 0 & 0 \\
0 & \mathbf{I} + [\frac{1}{2}\hat{\delta \boldsymbol{\theta}}]_{\times} & 0 \\
0 & 0 & \mathbf{I}_{9}
\end{bmatrix}
\end{aligned}
\end{equation}
위 행렬 중간 부분은 다음 과정을 통해 얻을 수 있다.새로운 nominal 상태의 방향 에러를 $\delta \boldsymbol{\theta}^{+}$라고 하고 기존의 에러를 $\delta \boldsymbol{\theta}$, 업데이트된 에러의 평균값을 $\hat{\delta \theta}$라고 하자. 이를 사용하여 다음과 같은 사실을 알 수 있다.
- true 방향 값은 error가 리셋될 때 변하지 않는다. i.e., $\mathbf{q}^{+}_{t} = \mathbf{q}_{t}$이다. \begin{equation}
\begin{aligned}
\delta \mathbf{q}^{+} \otimes \mathbf{q}^{+} = \delta \mathbf{q} \otimes \mathbf{q}
\end{aligned}
\end{equation} - 업데이트된 에러의 평균값은 nominal 상태에 적용된다.
\begin{equation}
\begin{aligned}
q^{+} = \hat{\delta \mathbf{q}} \otimes \mathbf{q}
\end{aligned}
\end{equation}
위 두 사실을 결합하여 $\delta \mathbf{q}^{+}$를 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\delta \mathbf{q}^{+} = \delta \mathbf{q} \otimes \hat{\delta \mathbf{q}}^{*} = [\hat{\delta \mathbf{q}}^{*}]_{R} \cdot \delta \mathbf{q}
\end{aligned}
\end{equation}
(\ref{eq:64})에 따라 충분히 작은 쿼터니언은 $\hat{\delta\mathbf{q}}^{*}\approx\begin{bmatrix}1\\-\frac{1}{2}\hat{\delta \boldsymbol{\theta}}\end{bmatrix}$와 같이 나타낼 수 있으므로 위 식은 다음과 같이 전개된다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} 1\\ \frac{1}{2}\delta \boldsymbol{\theta}^{+} \end{bmatrix}=\begin{bmatrix} 1&\frac{1}{2}\hat{\delta\boldsymbol{\theta}}^{\intercal}\\-\frac{1}{2}\hat{\delta \boldsymbol{\theta}}&\mathbf{I} + [\frac{1}{2}\hat{\delta \boldsymbol{\theta}}]_{\times}\end{bmatrix}\cdot\begin{bmatrix}1\\\frac{1}{2}\delta\boldsymbol{\theta}\end{bmatrix}+O(\left\|\delta\boldsymbol{\theta}\right\|^{2})
\end{aligned}
\end{equation}
위 식은 하나의 스칼라와 하나의 벡터 식으로 분리할 수 있다.
\begin{equation}
\begin{aligned}
&\frac{1}{4}\hat{\delta \boldsymbol{\theta}}^{\intercal}\delta\boldsymbol{\theta}=O(\left\|\delta\boldsymbol{\theta}\right\|^{2})\\
&\delta\boldsymbol{\theta}^{+}=-\hat{\delta\boldsymbol{\theta}}+\bigg(\mathbf{I}+\bigg[\frac{1}{2}\hat{\delta \boldsymbol{\theta}}\bigg]_{\times}\bigg)\delta\boldsymbol{\theta}+O(\left\|\delta\boldsymbol{\theta}\right\|^{2})
\end{aligned}
\end{equation}
위 첫번째 식은 고차항의 관련된 식이므로 크게 중요하지 않은 식이다. 하지만 위 두번째 식은 $\hat{\delta \boldsymbol{\theta}}^{+} = 0$ 일 때 리셋 연산을 의미하므로 중요한 식이다. 이를 통해 자코비안을 쉽게 구할 수 있다.
\begin{equation}
\begin{aligned}
\boxed{ \frac{\partial \delta \boldsymbol{\theta}^{+}}{\partial \delta \boldsymbol{\theta}} = \mathbf{I} + \bigg[\frac{1}{2} \hat{\delta \boldsymbol{\theta}} \bigg]_{\times} }
\end{aligned}
\end{equation}
이는 지역 좌표계일 때 자코비안과 비교했을 때 $+, -$ 부호만 바뀐 것을 알 수 있다.
References
[1] Sola, Joan. "Quaternion kinematics for the error-state Kalman filter." arXiv preprint arXiv:1711.02508 (2017).
'Fundamental' 카테고리의 다른 글
| [SLAM] 에러와 자코비안 정리(Errors and Jacobians) 정리 Part 2 (3) | 2023.01.13 |
|---|---|
| [SLAM] 에러와 자코비안 정리(Errors and Jacobians) 정리 Part 1 (17) | 2023.01.08 |
| [SLAM] 파티클 필터(Particle Filter) 개념 정리 (1) | 2022.10.07 |
| Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 2 (5) | 2022.08.31 |
| Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 1 (8) | 2022.08.27 |
 A L I D A
A L I D A





