[SLAM] Hand-eye Calibration 개념 정리 (+ Trajectory Evaluation)

본 포스트는 공부용으로 작성되었습니다.
틀린 부분이나 수정해야 할 부분이 있다면 말씀해주시면 확인 후 반영하겠습니다.

 
 
본 포스트에서는 Visual SLAM의 성능 평가를 위하여 ground truth (GT) 데이터를 취득한 후 주로 수행하는 Hand-eye calibration에 대해 설명한다. 
 
 

Introduction

Visual SLAM의 성능을 평가하기 위해서는 다양한 방법들이 존재하지만 실내에서는 주로 모션 캡쳐 시스템을 활용하여 ground truth (GT) 데이터를 취득한 후 성능을 평가한다. 모션 캡쳐 시스템은 일반적으로 카메라에 IR 반사 마커를 부착하여 GT 좌표계 $\{A\}$를 만든 후 실내에 고정된 여러 대의 카메라가 반사 마커를 추적하면서 GT trajectory를 만든다. 이 때, 모션 캡처 좌표계의 원점 $\{W\}$을 기준으로 트래킹하게 된다.
 
그러나 이렇게 얻은 GT trajectory를 바로 성능 평가에 사용하게 되면 SLAM trajectory와 GT trajectory의 원점이 다르므로 서로 다른 궤적이 만들어지게 된다. 따라서 Umeyama 방법과 같이 두 trajectory를 최대한 정렬(alignment)한 후 성능을 평가하는데 이 때, 어떻게 두 trajectory가 겹쳐지느냐에 따라 결과가 달라지므로 상대적으로 부정확한 결과를 얻을 확률이 높아진다. 따라서 이러한 문제를 해결하기 위해 GT 좌표계 $\{A\}$와 카메라 좌표계 $\{B\}$ 사이의 extrinsic parameters를 구하고자 하는 연구들이 진행되었는데 이 때 사용하는 캘리브레이션을 Hand-eye calibration이라고 한다.
 

즉, hand-eye calibration (이하 HE)은 위 그림에서 ${\mathbf{T}}_{AB}$를 구하는 것과 같다. ${\mathbf{T}}_{AB}$를 구하면 SLAM을 통해 trajectory가 생성되었을 때 GT trajectory와 동일하게 좌표계를 $\{W\}$로 일치시켜줄 수 있기 때문에 최적화를 통해 두 tracjetory를 겹치지 않아도 되고 따라서 보다 정확한 결과를 얻을 수 있다. 
 

Eye-in-hand calibration

HE는 로봇 베이스와 카메라 사이의 extrinsic을 구하는 방법(eye-to-hand)이 있고 로봇팔의 end effector와 팔 끝에 부착된 카메라 사이의 extinsic을 구하는 방법(eye-in-hand)이 있다. 본 포스트에서 설명할 GT 좌표계와 카메라 좌표계 사이의 extrinsic은 이 중 eye-in-hand를 사용하여 구할 수 있다.
본 포스팅에서는 GT 좌표계 $\{A\}$가 end effector의 역할을 대신한다. 즉, $\{W\}$가 로봇의 base coordinate인 원점이 되고 $\{A\}$가 hand coordinate, $\{B\}$가 eye coordinate이 되는 것이다. 이 때, $\{B\}$는 체커보드 좌표계 $\{C\}$를 원점으로 한다.
 

Problem formulation

모션 캡쳐 방에 체커보드(또는 circle, apriltags 등)를 놓고 카메라가 체커보드를 바라보면서 GT trajectory 로깅을 시작한다. 카메라가 움직일 때마다 IR 반사 마커도 같이 움직이므로 위 그림과 같이 두 개의 trajectory가 생성된다. $\{A\}$ 좌표계를 시작점으로 GT trajectory(1)가 생성되고 $\{B\}$ 좌표계를 시작점으로 Camera trajectory(2)가 생성된다. (1), (2)의 원점은 각각 $\{W\}$, $\{C\}$이다. (1)는 모션 캡쳐 시스템에 의해 생성되고 (2) 는 체커보드에 PnP를 수행하여 생성된다. 
 

두 trajectory에서 가장 앞의 $[t_1,t_2]$ 시간만을 표현하면 위 그림과 같다. $\{A_1\}$과 $\{A_2\}$의 위치가 서로 다르고 $\{B_1\}$과 $\{B_2\}$의 위치가 서로 다르지만 두 사이의 relative pose (=extrinsic) ${\mathbf{T}}_{AB}$는 항상 일정하다. 이를 통해 아래와 같은 수식을 유도할 수 있다.
 

$$\begin{array}{}\text{(1)}& \begin{array}{r}{\mathbf{T}}_{A_1{A}_2}{\mathbf{T}}_{AB}={\mathbf{T}}_{AB}{\mathbf{T}}_{B_1{B}_2}\end{array}\end{array}$$
위 식을 시각화하면 아래 그림과 같다.

즉, $\{A_1\}$ 좌표계에서 $\{B_2\}$ 좌표계로 변환하는 두 가지 방법이 있는데 두 방법이 결론적으로 동일함을 수식으로 표현한 것이다. 표기법을 단순화하면 다음과 같은 $\mathbf{X}$ 행렬을 구하는 문제가 된다.
$$\begin{array}{}\text{(2)}& \begin{array}{r}\mathbf{AX}=\mathbf{XB}\end{array}\end{array}$$
- $\mathbf{A}={\mathbf{T}}_{A_1{A}_2}$
- $\mathbf{B}={\mathbf{T}}_{B_1{B}_2}$
- $\mathbf{X}={\mathbf{T}}_{AB}$
 
위 공식은 순차적인 $[t_i,t_{i+1}]$ 뿐만 아니라 임의의 $[t_i,t_j]$에 대해서도 성립한다. 
 

How to solve $\mathbf{AX}=\mathbf{XB}$?

$\mathbf{AX}=\mathbf{XB}$를 구하는 문제는 주로  90년대에 연구되어오던 주제로 일반적으로 세 가지 방법이 존재한다. Tsai-Lenz(1989) [4], Park-Martin(1994) [5], Dual quaternions(1998) [6] 방법으로 해당 수식의 해를 구할 수 있다. 본 포스트에서는 이 중 서울대학교 박종우 교수님(Frank Park)이 제안하였던 Park-Martin 방법에 대해 설명한다.
 

Park-Martin method

Park-Martin 방법은 주어진 수식 $\mathbf{AX}=\mathbf{XB}$을 lie theory를 통해 식을 변형 후 해를 구하는 방법이다. 우선 주어진 수식을 분해하면 다음과 같다.
$$\begin{array}{}\text{(3)}& \begin{array}{rl}\mathbf{AX}& =\mathbf{XB}\\ \left[\begin{array}{cc}{\mathbf{R}}_A& {\mathbf{t}}_A\\ 0& 1\end{array}\right]\left[\begin{array}{cc}{\mathbf{R}}_X& {\mathbf{t}}_X\\ 0& 1\end{array}\right]& =\left[\begin{array}{cc}{\mathbf{R}}_X& {\mathbf{t}}_X\\ 0& 1\end{array}\right]\left[\begin{array}{cc}{\mathbf{R}}_B& {\mathbf{t}}_B\\ 0& 1\end{array}\right]\\ \\ {\mathbf{R}}_A{\mathbf{R}}_X& ={\mathbf{R}}_X{\mathbf{R}}_B\cdots \text{[1]}\\ {\mathbf{R}}_A{\mathbf{t}}_X+{\mathbf{t}}_A& ={\mathbf{R}}_X{\mathbf{t}}_B+{\mathbf{t}}_X\cdots \text{[2]}\end{array}\end{array}$$
 
위 $[2]$ 식을 정리하면 다음과 같다.
$$\begin{array}{}\text{(4)}& \begin{array}{r}({\mathbf{R}}_A-\mathbf{I}){\mathbf{t}}_X={\mathbf{R}}_X{\mathbf{t}}_B-{\mathbf{t}}_A\cdots \text{[2]}\end{array}\end{array}$$
 
따라서 순차적으로 $[1]$ 식에서 ${\mathbf{R}}_X$를 구한 후 $[2]$ 식에 대입하여 ${\mathbf{t}}_X$를 구한다.
 

Find ${\mathbf{R}}_X$

우선 ${\mathbf{R}}_A{\mathbf{R}}_X={\mathbf{R}}_X{\mathbf{R}}_B$ 식을 변형한다. 좌항의 ${\mathbf{R}}_X$를 우항으로 넘기면 ${\mathbf{R}}_A={\mathbf{R}}_X{\mathbf{R}}_B{\mathbf{R}}_X^{⊺}$이 된다. 그리고 양변에 logarithmic mapping을 수행하면 다음과 같다.
$$\begin{array}{}\text{(5)}& \begin{array}{r}\text{log}({\mathbf{R}}_A)=\text{log}({\mathbf{R}}_X{\mathbf{R}}_B{\mathbf{R}}_X^{⊺})\end{array}\end{array}$$
 
이 때, $\text{log}({\mathbf{R}}_A)$를 $[\alpha {]}_{\times }$와 같이 lie algebra of SO(3)로 나타낼 수 있고 $\text{log}({\mathbf{R}}_B)$ 또한 $[\beta {]}_{\times }$와 같이 나타낼 수 있다. 
- $\alpha \in {\mathbb{R}}^3$ : angular velocity vector
- $\beta \in {\mathbb{R}}^3$ : angular velocity vector
- $[\alpha {]}_{\times }\in {\mathbb{R}}^{3\times 3}$ : lie algebra of SO(3) ${\mathbf{R}}_A$
- $[\beta {]}_{\times }\in {\mathbb{R}}^{3\times 3}$ : lie algebra of SO(3) ${\mathbf{R}}_B$
- $[\cdot {]}_{\times }$ : skew symmetric matrix
 
($\text{5}$) 식을 치환하여 다시 나타내면 $[\alpha {]}_{\times }={\mathbf{R}}_X[\beta {]}_{\times }{\mathbf{R}}^{⊺}$이 된다. 그리고 ${\mathbf{R}}_X[\beta {]}_{\times }{\mathbf{R}}^{⊺}=[{\mathbf{R}}_X\beta {]}_{\times }$이므로 아래 식이 성립한다. 위 식들은 adjoint matrix of SO(3)의 성질에 의해 유도되었다.
$$\begin{array}{}\text{(6)}& \begin{array}{rl}& [\alpha {]}_{\times }=[{\mathbf{R}}_X\beta {]}_{\times }\\ & \to \alpha ={\mathbf{R}}_X\beta \end{array}\end{array}$$
 

Lie theory에서 adjoint matrix of SO(3)의 성질로 인해 다음과 같은 유용한 관계들이 도출된다.
$$\begin{array}{}\text{(7)}& \begin{array}{rl}& \exp ([\mathbf{R}\omega {]}_{\times })=\mathbf{R}\exp ([\omega {]}_{\times }){\mathbf{R}}^{⊺}=\exp (\mathbf{R}[\omega {]}_{\times }{\mathbf{R}}^{⊺})\end{array}\end{array}$$

위 변환 관계는 많이 활용되기 때문에 알아놓으면 유용하다. Adjoint matrix에 대한 더 자세한 내용은 Lie Theory 개념 정리 포스트를 참조하면 된다.

 

Solve least squares for ${\mathbf{R}}_X$

현실 세계의 데이터는 노이즈가 반드시 포함되어 있으므로 ${\mathbf{A}}_i\mathbf{X}=\mathbf{X}{\mathbf{B}}_i$가 성립하지 않는다. 따라서 에러를 최소화해주는 최적해 ${\mathbf{X}}^{\ast }$를 최소제곱법(least squares)으로 풀어야 한다. 
$$\begin{array}{}\text{(8)}& \begin{array}{r}\eta =\sum _{i=1}^{k}d({\mathbf{A}}_i\mathbf{X},\mathbf{X}{\mathbf{B}}_i)\end{array}\end{array}$$
- $\eta$: 에러의 총합
- $d(\cdot ,\cdot )$: 두 SE3군 사이의 거리를 측정해주는 함수. 측정 방식에 따라 다양한 함수를 정의할 수 있다.
 
일반적으로 위 식은 SE3군을 포함하므로 비선형 최소제곱법(non-linear least squares)을 통해 풀어야 한다. Park-martin 방법은 위 식을 이전에 유도한 $\alpha ={\mathbf{R}}_X\beta$로 치환함으로써 선형 최소제곱법의 closed form solution을 얻을 수 있다.
$$\begin{array}{}\text{(9)}& \begin{array}{r}{\eta }_1=\sum _{i=1}^k{\Vert {\mathbf{R}}_X{\beta }_i-{\alpha }_i\Vert }^2\end{array}\end{array}$$
 
위 식에서 회전행렬 ${\mathbf{R}}_X$을 구하려면 비선형 최소제곱법으로 풀어야 한다고 생각할 수 있으나 Nadas [7]가 제안한 방법을 사용하면 선형 최소제곱법으로 풀 수 있다. 따라서 다음과 같은 closed form solution이 존재한다.
$$\begin{array}{}\text{(10)}& \boxed{{\displaystyle \begin{array}{r}{\mathbf{R}}_X=({\mathbf{M}}^{⊺}\mathbf{M}{)}^{-1/2}{\mathbf{M}}^{⊺}\end{array}}}\end{array}$$
- $\mathbf{M}=\sum _i{\beta }_i{\alpha }_i^{⊺}$
 
위 식의 자세한 유도 과정에 대해 궁금한 독자들은 [7]을 참조하면 된다.
 

Find ${\mathbf{t}}_X$

Solve least squares for ${\mathbf{t}}_X$

${\mathbf{R}}_X$를 구한 다음 아래 식에 대입함으로써 ${\mathbf{t}}_X$를 구할 수 있다.
$$\begin{array}{}\text{(11)}& \begin{array}{r}{\eta }_2=\sum _{i=1}^k{\Vert ({\mathbf{R}}_{A_i}-\mathbf{I}){\mathbf{t}}_X-{\mathbf{R}}_X{\mathbf{t}}_{B_i}+{\mathbf{t}}_{A_i}\Vert }^2\end{array}\end{array}$$
 
위 식은 ${\Vert \mathbf{C}{\mathbf{t}}_X-\mathbf{d}\Vert }^2$ 꼴이므로 다음과 같이 일반적인 선형 최소제곱법 해를 사용하여 ${\mathbf{t}}_X$를 구할 수 있다.
$$\begin{array}{}\text{(12)}& \boxed{{\displaystyle \begin{array}{r}{\mathbf{t}}_X=({\mathbf{C}}^{⊺}\mathbf{C}{)}^{-1}{\mathbf{C}}^{⊺}\mathbf{d}\end{array}}}\end{array}$$
- $\mathbf{C}=\mathbf{I}-{\mathbf{R}}_{A_i}$
- $\mathbf{d}={\mathbf{t}}_{A_i}-{\mathbf{R}}_X{\mathbf{t}}_{B_i}$
 
 

Code implementation

OpenCV에서 handeye calibration 관련 함수들을 보면 calibrateHandEyePark() 이라는 함수가 존재한다[3]. 해당 함수가 Park-Martin 방법을 사용하여 HE를 수행하는 코드이다.
 

//Reference:
//F. Park, B. Martin, "Robot Sensor Calibration: Solving AX = XB on the Euclidean Group."
//In IEEE Transactions on Robotics and Automation, 10(5): 717-721, 1994.
//Matlab code: http://math.loyola.edu/~mili/Calibration/
static void calibrateHandEyePark(const std::vector<Mat>& Hg, const std::vector<Mat>& Hc,
                                 Mat& R_cam2gripper, Mat& t_cam2gripper)
{
    Mat M = Mat::zeros(3, 3, CV_64FC1);

    for (size_t i = 0; i < Hg.size(); i++)
    {
        for (size_t j = i+1; j < Hg.size(); j++)
        {
            Mat Hgij = homogeneousInverse(Hg[j]) * Hg[i];
            Mat Hcij = Hc[j] * homogeneousInverse(Hc[i]);

            Mat Rgij = Hgij(Rect(0, 0, 3, 3));
            Mat Rcij = Hcij(Rect(0, 0, 3, 3));

            Mat a, b;
            Rodrigues(Rgij, a);
            Rodrigues(Rcij, b);

            M += b * a.t();
        }
    }

    Mat eigenvalues, eigenvectors;
    eigen(M.t()*M, eigenvalues, eigenvectors);

    Mat v = Mat::zeros(3, 3, CV_64FC1);
    for (int i = 0; i < 3; i++) {
        v.at<double>(i,i) = 1.0 / sqrt(eigenvalues.at<double>(i,0));
    }

    Mat R = eigenvectors.t() * v * eigenvectors * M.t();
    R_cam2gripper = R;

    int K = static_cast<int>((Hg.size()*Hg.size() - Hg.size()) / 2.0);
    Mat C(3*K, 3, CV_64FC1);
    Mat d(3*K, 1, CV_64FC1);
    Mat I3 = Mat::eye(3, 3, CV_64FC1);

    int idx = 0;
    for (size_t i = 0; i < Hg.size(); i++)
    {
        for (size_t j = i+1; j < Hg.size(); j++, idx++)
        {
            Mat Hgij = homogeneousInverse(Hg[j]) * Hg[i];
            Mat Hcij = Hc[j] * homogeneousInverse(Hc[i]);

            Mat Rgij = Hgij(Rect(0, 0, 3, 3));

            Mat tgij = Hgij(Rect(3, 0, 1, 3));
            Mat tcij = Hcij(Rect(3, 0, 1, 3));

            Mat I_tgij = I3 - Rgij;
            I_tgij.copyTo(C(Rect(0, 3*idx, 3, 3)));

            Mat A_RB = tgij - R*tcij;
            A_RB.copyTo(d(Rect(0, 3*idx, 1, 3)));
        }
    }

    Mat t;
    solve(C, d, t, DECOMP_SVD);
    t_cam2gripper = t;
}

 

SLAM trajectory evaluation 

필자가 생각하는 실내에서 Visual SLAM 성능을 평가하기 위한 과정은 다음과 같다.

1. 모션 캡쳐 장비를 사용하여 GT trajectory 데이터를 획득하고 동시에 센서 데이터를 로깅한다.
2. 체커보드(또는 circle, apriltags 등)을 놓고 HE를 위한 데이터 로깅을 수행한다.
3. HE를 수행하여 GT 좌표계(hand)와 카메라 좌표계(eye) 간 extrinsic을 구한다.
4. 센서 데이터를 사용하여 SLAM trajectory를 생성한다.
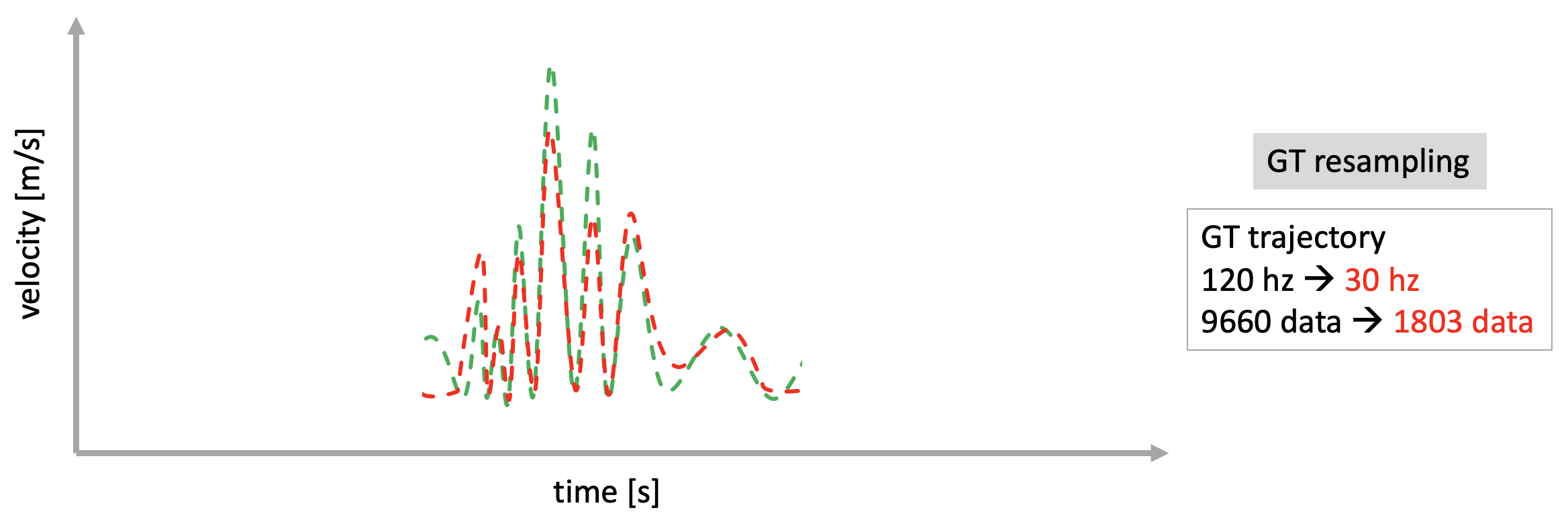
5. SLAM trajectory와 GT trajectory의 시작 지점과 샘플링 주기가 서로 다르므로 이를 맞춰준다.
6. SLAM trajectory에 extrinsic을 적용한 후 GT trajectory와 정렬하여 성능 평가를 수행한다.

 
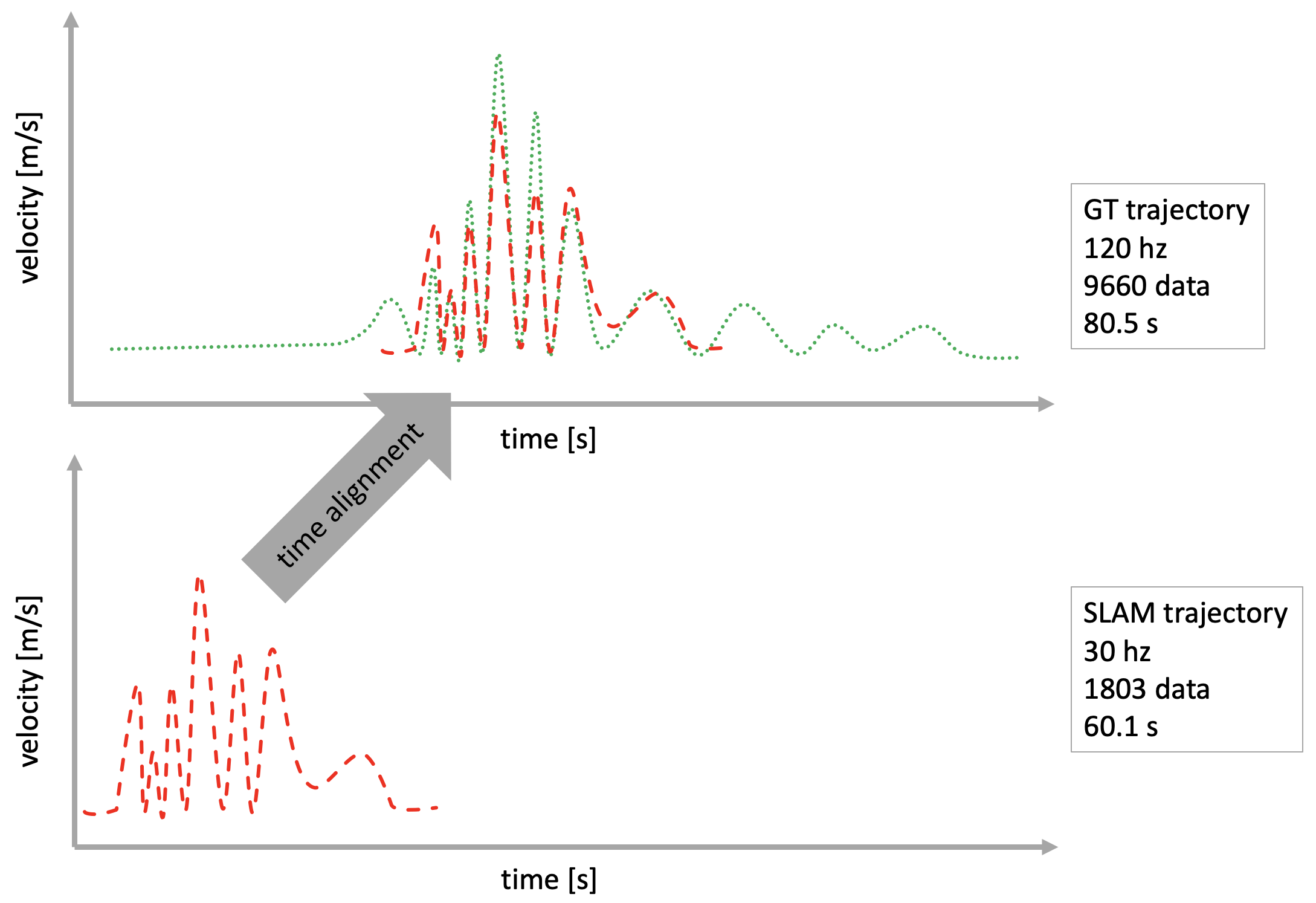
이 때, 간과하기 쉬운 부분이 5번 과정이다. SLAM에서 로깅한 trajectory 정보와 GT trajectory 정보는 서로 다른 주기로 로깅되었기 때문에 시간 간격이 다르다. 또한 GT trajectory의 시작 지점과 SLAM trajectory의 시작 지점이 서로 다르기 때문에 이에 대한 고려없이 바로 trajectory evaluation을 수행한다면 정확한 성능 평가 결과를 얻을 수 없다. 따라서 이러한 문제를 해결하기 위해서 주기가 다른 두 신호를 정렬하는 방법을 사용해야 한다.

예를 들어, 위와 같은 데이터를 수집했다고 가정해보자. x축은 시간을 의미하고 y축은 속도(velocity)를 의미한다. 두 데이터의 위치(position)은 아직 정렬되어 있지 않으므로 선형적으로 비교할 수 없다. 따라서 속도를 비교한다.

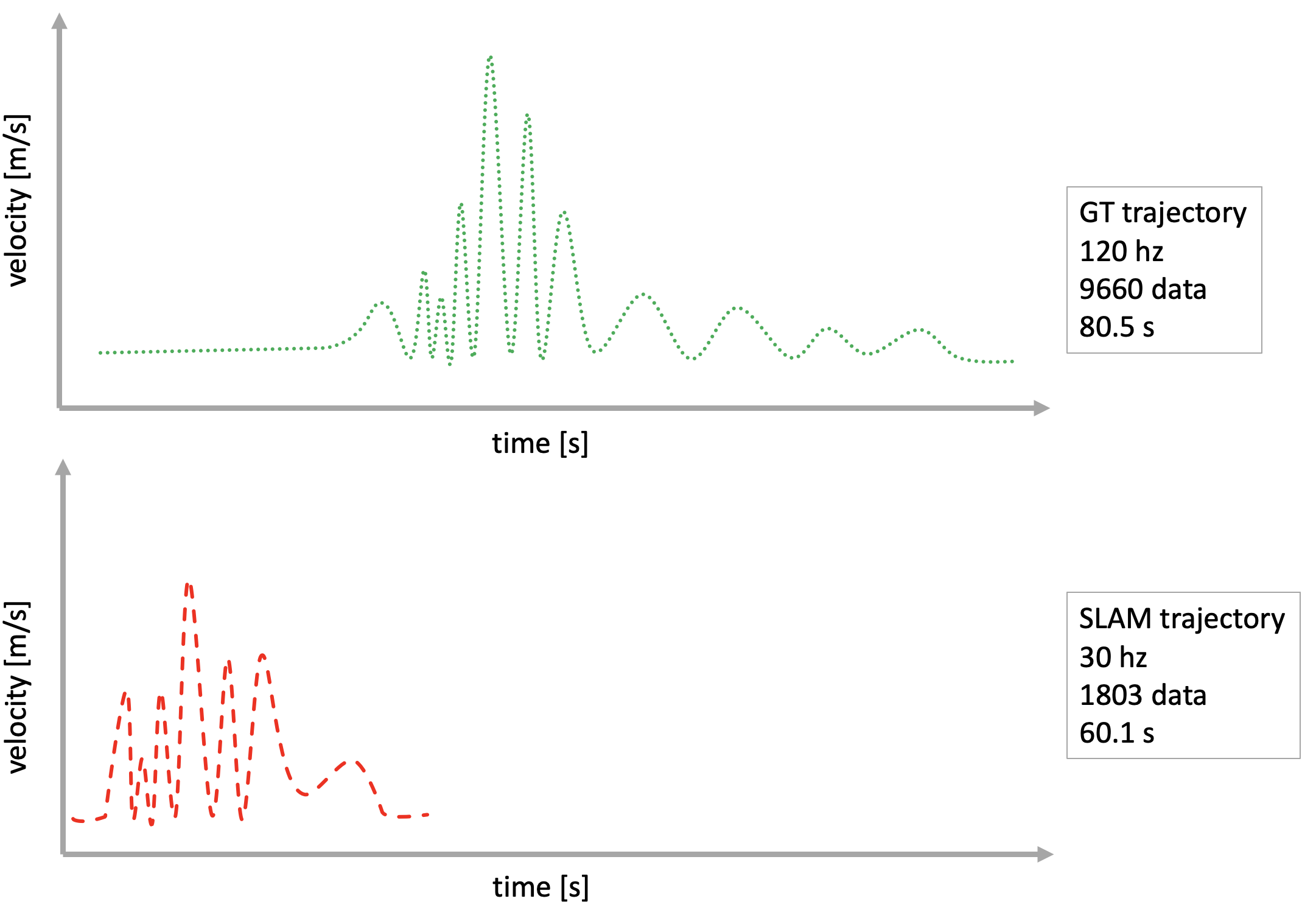
time alignment using cross-correlation

Cross-correlation을 사용하면 주기가 서로 다른 두 샘플링 신호의 시간 지연 $dt$를 구할 수 있다. SLAM trajectory에서는 신호가 곧 시간을 의미하므로 두 trajectory의 시작 시간을 정렬해주는 효과를 가진다. [8]를 보면 cross-correlation을 사용하여 $dt$ 를 구하는 구체적인 예시를 볼 수 있다. 일반적으로 GT 데이터가 SLAM 데이터보다 주기도 빠르고 데이터량도 많기 때문에 SLAM 데이터에서 $dt$만큼 데이터를 이동시킨다. 

Resampling

$dt$만큼 SLAM 데이터가 이동하였으면 이제 두 데이터의 샘플링 주기를 동일하게 맞춰야 한다. 예를 들어, GT 데이터가 120hz로 9660개만큼 로깅되고 SLAM 데이터 30hz로 1803개만큼 로깅되었었다면 동일한 시간대에서 GT 데이터를 30hz, 1803개로 다운샘플링한다. 이 때 GT 데이터를 spline으로 표현하여 빈 시간 부분이 있다면 보간한다.

 

References

[1] Hand-Eye Calibration - TUM
[2] OpenCV - calibrateHandeye() 
[3] github - OpenCV calibrateHandEyePark()
[4] R. Y. Tsai and R. K. Lenz, "A new technique for fully autonomous and efficient 3D robotics hand/eye calibration." In IEEE Transactions on Robotics and Automation, vol. 5, no. 3, pp. 345-358, June 1989.
[5] F. Park, B. Martin, "Robot Sensor Calibration: Solving AX = XB on the Euclidean Group." In IEEE Transactions on Robotics and Automation, 10(5): 717-721, 1994.
[6] K. Daniilidis, "Hand-Eye Calibration Using Dual Quaternions." In The International Journal of Robotics Research,18(3): 286-298, 1998. 
[7] Nadas, A., 1978. Least squares and maximum likelihood estimates of rigid motion. IBM Res. Rep.
[8] Cross-correlation signal alignment - gist