본 포스트는 필자가 확률 이론을 공부하면서 정리한 내용이다.
랜덤 프로세스(Random Process), 가우시안 프로세스(Gaussian Process)에 대해 알고 싶으면 확률 이론(Probability Theory) 개념 정리 Part 2 포스팅을 참조하면 된다.
선형대수학에 대해 알고 싶으면 선형대수학 (Linear Algebra) 개념 정리 Part1, 선형대수학 (Linear Algebra) 개념 정리 Part2 포스트를 참조하면 된다.
Kalman filter (KF, EKF, ESKF)에 대해 알고 싶으면 칼만 필터(Kalman Filter) 개념 정리 포스트를 참조하면 된다.
Particle filter에 대해 알고 싶으면 파티클 필터(Particle Filter) 개념 정리 포스트을 참조하면 된다.
NOMENCLATURE of Probability Theory
- 확률(probability)는 $Pr(\cdot)$으로 표기한다.
- 사건(event)은 대문자로 표기힌다. e.g., $A,B$
- 이산 확률질량함수(pmf)와 연속 확률밀도함수(pdf)는 각각 $P(\cdot)$와 $p(\cdot)$으로 표기한다.
- 확률변수(random variable)는 소문자로 표기한다. e.g., $x,y$
- 확률 $\Pr(\cdot)$는 사건을 입력으로 받아 $[0,1]$의 값을 반환한다. (e.g., $\Pr(A), \Pr(A\mid B)$)
- pmf/pdf는 확률변수 $x$의 값을 입력으로 받아 확률(이산) 또는 밀도(연속)를 반환하는 함수이다. e.g., $P(x), p(x)$
Introduction
현대 확률론의 수학적인 정의는 20세기 수학자 Andrey Kolmogorov에 의해 정립되었다. 이번 섹션에서는 확률론을 설명하기 위한 기반 이론이 되는 set theory와 measure theory을 설명한다. 해당 이론에 대한 대부분의 내용은 [6]를 참고하여 작성하였다.
Set theory
집합론(set theory)은 수학의 기본적인 개념인 집합과 그 집합들 간의 관계, 연산 등을 연구하는 수학의 한 분야이다. 집합론은 수학의 거의 모든 분야에 걸쳐 기초적인 언어와 도구를 제공한다. 다양한 집합론의 용어를 먼저 정의해보자. 옷장과 옷으로 비유하여 생각해보면
- 집합(set)이란 옷장을 의미하고
- 원소(element)란 옷을 의미한다.
- 부분집합(subset)이란 옷들 중 일부분을 의미하며
- 전체집합(universal set)은 옷장의 모든 옷을 의미한다.
- 집합 연산자(set operator)는 옷으로 할 수 있는 연산(e.g., 옷이 몇개 있는가)을 의미한다.
- 서로소 집합(disjoint set)은 청바지와 코트처럼 교집합이 없는 집합을 의미한다($A \cap B = \emptyset$)
- 분할(partition of A)는 집합 A를 서로소 집합으로 나누는 것을 의미한다. $A=\{1,2,3,4\} \rightarrow \{\{1,2\}, \{3\}, \{4\}\}$
- 곱집합(Cartesian product, 데카르트 곱)은 두 집합 A,B가 있을 때 각각의 집합에서 한 개씩 가져와서 쌍(pair)를 이루는 것을 말한다. $A\times B = \{(a,b) : a \in A, b \in B \}$. 왼쪽 예시는 2차원 벡터 공간 $\mathbb{R}^{2}$의 예시이다.
- 멱집합(power set)은 집합 A의 모든 부분집합의 집합을 의미하며 $2^A$로 표기한다. $A=\{1,2,3\}$인 경우 멱집합은 $\{\emptyset, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\} \}$과 같이 8개가 된다.
Cardinality
집합 $A$의 크기(cardinality)는 $|A|$와 같이 표기한다. $|A|=m$이고$|B|=n$이면 둘의 곱집합은 $|A\times B| = mn$이 된다.
- 멱집합의 cardinality는 $|A|=n$인 경우 $|2^A|=2^n$이 된다.
- 만약 두 집합이 일대일 대응(one-to-one correspondence)을 보인다면 두 집합의 cardinality는 동일하다.
- 가산집합(countable set)은 자연수와 일대일 대응을 이루는 함수로 셀 수 있는(countable) 집합을 말한다. 셀 수 있다고 반드시 유한할 필요는 없다.
- 자연수 집합과 분수들의 집합과 같이 셀 수 있으나 크기가 무한인(countable infinite) 집합을 가부번(denumerable) 집합이라고 한다. 또는 aleph null($\aleph_{0}$)이라고도 부른다.
- 비가산집합(uncountable set)이란 가산집합과 달리 셀 수 없는 집합을 말하며 $\mathbf{c}$(continuum)라고 부르거나 $\mathbf{c} = 2^{\aleph_{0}}$라고 표기한다. 예를 들면 0과 1 사이의 실수의 개수들의 집합이 비가산 집합에 해당한다.
Function
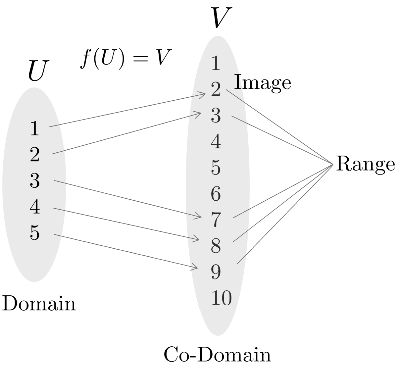
함수 $f$는 집합 $U$에서 다른 집합 $V$로 변환 또는 매핑하는 연산자를 말한다.
\begin{equation}
\begin{aligned}
f : U \rightarrow V
\end{aligned}
\end{equation}
이 때, $U$를 정의역(domain)이라고 부르며 $V$를 공역(co-domain)이라고 한다. 상(image)이란 주어진 입력 $U$에 대해 매핑된 출력 $V$를 의미한다. 치역(range)이란 정의역 내에 있는 입력 $U$들에 의해 매핑된 모든 출력 $V$의 집합을 의미한다.
- domain $U$, co-domain $V$
- image: $f(A) = \{ f(x) \in V : x \in A \}, A \subseteq U$
- range: $f(U)$
- inverse image(=preimage) : $f^{-1}(B) = \{ x \in U : f(x) \in B \}, B \subseteq V$

Onto는 전사함수(surjective)라고도 불리며 공역이 치역과 같은 경우를 의미한다. 이는 co-domain의 모든 원소들이 사영된 것을 의미한다. One-to-one은 일대일함수(injective)라고도 불리며 정의역의 원소와 공역의 원소가 하나씩 대응되는 함수를 의미한다. 함수 $f$가 역함수 $f^{-1}$를 가지기 위해서는(invertible) 전사함수이면서 동시에 일대일 함수이어야 한다.
Measure theory
측도론(measure theory)은 크기, 길이, 면적, 부피 등을 일반화한 측도(measure)의 개념을 다루는 수학의 분야이다. 이 이론은 특히 확률론과 함수해석학에서 중요한 역할을 한다. 측도론의 기본적인 아이디어는 집합에 숫자를 할당하여 그 집합의 크기를 측정하는 것이다.
예를 들어, 실수 집합의 부분집합에 대해 길이를 할당할 수 있고, 이를 통해 무한대의 집합이나 아주 작은 집합의 크기를 정량화할 수 있다. 집합 함수(set function)란 하나의 집합에 하나의 값(measure)을 할당하는 함수를 말한다. 이는 앞서 말한 것처럼 크기, 길이, 면적, 부피 등이 될 수 있다.
$\sigma$-field
$\sigma$-field $\mathcal{B}$란 '측정 가능한 집합'들을 정의하기 위한 집합들의 컬렉션을 의미한다. 100명의 사람들의 몸무게를 재는 것으로 비유하여 $\sigma$-field를 만족하기 위한 세 가지 정의를 살펴보자.
- $\emptyset \in \mathcal{B}$ : 공집합을 포함해야 한다(e.g., 아무 사람의 몸무게도 재지 않은 기준점이 필요하다).
- $A \in \mathcal{B} \Rightarrow A^c \in \mathcal{B}$: 어떤 집합 $A$가 $\sigma$-field에 속한다면 이의 여집합 $A^c$ 또한 $\sigma$-field에 속해야 한다(e.g., 2명에 대해 몸무게를 잴 수 있다면 98명에 대해서도 몸무게를 잴 수 있어야 한다.).
- $A_i \in \mathcal{B} \Rightarrow \cup_{i=1}^{\infty}A_i \in \mathcal{B}$: $\sigma$-field에 속하는 임의의 집합 시퀀스 $A_i, i=1,2,\cdots$에 대하여 이 집합들의 합집합도 $\sigma$-field에 속해야 한다(e.g., a라는 사람의 몸무게를 잴 수 있고 b라는 사람의 몸무게를 잴 수 있다면 a+b 둘을 합쳤을 때도 몸무게를 잴 수 있어야 한다).
Properties of $\sigma$-field
- 전체집합 $U$을 포함한다. : $U \in \mathcal{B}$
- 가산 합집합(countable union)에 대하여 닫혀있다. : $A_i \in \mathcal{B} \Rightarrow \cup_{i=1}^{\infty}A_i \in \mathcal{B}$
- 가산 교집합(countable intersection)에 대하여 닫혀있다. : $A_i \in \mathcal{B} \Rightarrow \cap_{i=1}^{\infty}A_i \in \mathcal{B}$
- 멱집합 $2^U$는 가장 잘게 나눌 수 있는 $\sigma$-field이다.
- 유한할 수 있고(finite) 셀 수 없을 수 있으나(uncountable) 가부번할 수 없다(never denumerable).
- $\mathcal{B}, \mathcal{C}$가 $\sigma$-field인 경우 $\mathcal{B} \cap \mathcal{C}$은 $\sigma$-field이지만 $\mathcal{B} \cup \mathcal{C}$은 $\sigma$-field가 아니다.
- 집합 $A$에 대하여 만들어진 $\sigma$-field는 $\sigma(A)$와 같이 표기한다.
Measurable space
임의의 집합 $U$와 $U$의 부분집합으로 이루어진 $\sigma$-field $\mathcal{B}$가 주어졌다면 가측공간(measurable space)는 $(U, \mathcal{B})$ 같이 정의할 수 있다.
측도(measure) $\mu$란 가측공간 $(U, \mathcal{B})$에서 $\sigma$-field의 원소를 사용하여 $[0,\infty]$의 값을 반환하는 일종의 집합 함수(set function)을 말한다.
\begin{equation}
\begin{aligned}
\mu : \mathcal{B} \rightarrow [0, \infty]
\end{aligned}
\end{equation}
- $\mu(\emptyset) = 0$ : 공집합에 대한 측도는 $0$이다.
- 서로소 집합들 $A_i$, $A_j$들에 대하여 $\mu(\cup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty} \mu(A_i)$가 성립한다.
- 100명의 몸무게를 잴 때 1~10번(A) 사람의 몸무게를 잰 것과 65-75번(B) 사람의 몸무게를 잰 것은 서로 다르지만 이 두 집합을 뭉쳐서(A+B) 한 번에 몸무게를 잰 것과 각 집합(A,B)들의 몸무게를 잰 값을 더한 값은 서로 같아야 한다.
- 가측공간과 측도를 합하여 $(U, \mathcal{B}, \mu)$와 같이 표기하기도 한다.
Probability
측도론에서 확률(probability)이란 전체집합 $U$에 대하여 $\mu(U)=1$의 크기를 만족하도록 정규화된 측도(normalized measure)를 의미한다.
Random experiment
1부터 6까지 나올 확률이 모두 동일한 주사위(fair dice)가 주어졌다고 하자. 전체 집합 $U=\{1,2,3,4,5,6\}$에 대한 $\sigma$-field $\mathcal{B}$는 어떻게 정할까? 확률 문제는 일반적으로 다음과 같은 질문을 묻는다.
- 주사위가 1이 나올 확률은 얼마인가?
- 주사위가 4 또는 6이 나올 확률은 얼마인가?
- 주사위가 2,3,5 중 하나가 나올 확률은 얼마인가?
이와 같이 집합 $U$에 대한 모든 부분집합을 사용할 수 있어야 되기 때문에 $\mathcal{B}$는 보통 멱집합 $2^U$을 사용한다. 확률에서 가측공간 $(U, \mathcal{B}, \mu)$는 특별히 확률공간(probability space)라고 하며 일반적으로 $(\Omega, \mathcal{F}, Pr)$로 표기한다. 각 기호들의 설명은 다음과 같다.
- $\Omega$: 표본공간(sample space)라고 하며 이름은 공간이 들어가지만 나올 수 있는 원소들의 전체 집합(=set)을 의미한다.
- $\mathcal{F}$: 표본공간의 부분집합을 의미하며 사건(event)이라고 부른다.
- $Pr$: 측도(measure)를 수행하는 연산자로써 표본공간의 원소에 확률을 부여하는 역할을 한다.
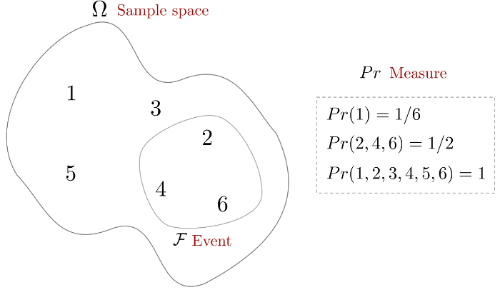
어떠한 현상으로부터 결과를 얻기 위해서는 실험(experiment)를 해야하고 이 때 우리는 실현값(outcome)을 얻을 수 있다. 만약 실험의 결과가 매 번 다르고 우리가 실현값의 결과를 하나의 표본공간으로 정의할 수 있다고 하면 이는 확률 실험(random experiment)라고 부른다.
따라서 주사위 던지기는 확률 실험의 일종이며 우리는 표본공간 $\Omega=\{1,2,3,4,5,6\}$에서 확률 $Pr(\cdot)$이라는 측도(measure)를 사용하여 공간 내 원소의 크기를 측정한 실현값(outcome)을 얻을 수 있다.
\begin{equation}
\begin{aligned}
& Pr(1) = Pr(2) = Pr(3) = Pr(4) = Pr(5) = Pr(6) = 1/6 \\
& Pr(A) = Pr(2,4,6) = Pr(2)+Pr(4)+Pr(6) = 1/2
\end{aligned}
\end{equation}
Probability axioms
확률공간 $(\Omega, \mathcal{F}, Pr)$에 정의된 확률 $Pr(\cdot)$은 하나의 집합 함수(set function)이며 다음과 같이 정의된다.
\begin{equation}
\begin{aligned}
Pr(\mathcal{F}) \rightarrow [0,1]
\end{aligned}
\end{equation}
확률의 공리(axiom)는 다음과 같다.
- $Pr(\emptyset) = 0$ : 공집합에 대한 측도는 $0$이다.
- $Pr(A) \geq 0 \quad \forall A \subseteq \Omega$ : 확률은 항상 0보다 크거나 같은 값을 가진다.
- 서로소 집합들 $A_i$, $A_j$들에 대하여 $Pr(\cup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty} Pr(A_i)$가 성립한다.
- $Pr(\Omega) = 1$ : 전체 표본공간에 대한 확률의 총량은 $1$이다.
위 조건에서 보다시피 확률이란 기존 측도(measure)의 세가지 조건에 마지막 조건(총합=1)이 추가된 특수한 버전으로 해석할 수 있다.
Probability allocation function
지금까지 확률공간 $(\Omega, \mathcal{F}, Pr)$을 정의하였고 표본공간의 부분집합인 $\mathcal{F}$의 크기를 측도(measure)함으로써 확률을 측정할 수 있는 연산자 $Pr$를 정의하였다. 서로 다른 표본공간에서 대하여 각각 측도 $Pr$를 수행할 수 있는 함수 $P(\cdot), p(\cdot)$를 정의할 수 있고 이를 확률할당함수(probability allocation function)이라고 한다.
이산(discrete) 표본공간 $\Omega$:
\begin{equation}
\begin{aligned}
& \boxed{ P : \Omega \rightarrow [0,1] } \\
& \text{ such that } \\
& \qquad \sum_{w \in \Omega} P(w) = 1 \\
& \qquad Pr(A) = \sum_{w\in A} P(w)
\end{aligned}
\end{equation}
연속(continuous) 표본공간 $\Omega$:
\begin{equation}
\begin{aligned}
& \boxed{ p : \Omega \rightarrow [0,\infty) } \\
& \text{ such that } \\
& \qquad \int_{w \in \Omega} p(w)dw=1 \\
& \qquad Pr(A) = \int_{w\in A} p(w) dw
\end{aligned}
\end{equation}
일반적으로 전자를 확률질량함수(probability mass function, pmf)라고 하며 후자를 확률밀도함수(probability density function, pdf)라고 한다.
이 때 이산/연속의 구분은 보통 표본공간 $\Omega$ 자체의 성질이라기보다 관심 있는 확률변수 $x$의 분포가 어떤 형태로 표현되는지에 대한 구분으로 이해하면 된다. 즉, 이산형이면 pmf $P(x)$로 연속형이면 pdf $p(x)$로 분포를 기술하는 경우가 많다. 표본공간 $\Omega$는 실험 결과를 모델링하기 위한 공간이며 같은 분포도 서로 다른 $\Omega$ 위에서 구성될 수 있다.
Independence != disjoint
두 사건(event) $A, B$이 서로 독립 사건임을 보이기 위해서는 다음의 정의를 만족해야 한다.
\begin{equation}
\begin{aligned}
& Pr(A\cap B) = Pr(A) Pr(B) \\ & Pr(A|B) = Pr(A)
\end{aligned}
\end{equation}
위 정의에서 알 수 있듯이 독립(independent)은 한 사건의 발생이 다른 사건의 확률에 영향을 주지 않는다는 뜻이다.
반면 서로소(disjoint), 즉 상호 배제(mutually exclusive)란 두 사건이 동시에 일어날 수 없음을 의미하며 $A\cap B=\varnothing$로 쓴다.
만약 $A\cap B=\varnothing$이면
\begin{equation}
\begin{aligned}
Pr(A\cap B)=0 \quad \cdots \text{disjoint}
\end{aligned}
\end{equation}
이므로 $Pr(A)>0$ 그리고 $Pr(B)>0$인 경우에는 $Pr(A\cap B)=Pr(A)Pr(B)$를 만족할 수 없어 $A,B$는 독립일 수 없다. ($Pr(A)=0$ 또는 $Pr(B)=0$의 경우에는 위 등식이 우연히 성립할 수 있다.)
Joint probability

결합 확률(joint probability)이란 두 사건 $A,B$가 동시에 발생할 확률(=교집합이 발생할 확률)을 의미한다.
\begin{equation}
\begin{aligned}
& Pr(A \cap B) \end{aligned}
\end{equation}
Marginal probability
주변 확률(marginal probability)는 여러 사건들 사이에서 하나의 사건만을 고려하는 것을 말한다. 예를 들어, 두 사건 $A$와 $B$가 있고, 이들의 결합 확률(joint probability)가 주어졌을 때, $A$의 주변 확률은 $B$가 취할 수 있는 모든 값에 대해 $A$의 확률을 합하여 얻어진다. $\{B_i\}$가 서로소(disjoint)이고 $\bigcup_i B_i=\Omega$인 분할(partition)일 때 다음이 성립한다(law of total probability)
\begin{equation}
\begin{aligned}
Pr(A) = \sum_{i} Pr(A \cap B_i)
\end{aligned}
\end{equation}
Conditional probability
조건부 확률은 두 사건 $A,B$에 대하여 $B$가 발생했을 때 $A$가 발생할 확률을 의미한다.
\begin{equation}
\begin{aligned}
Pr(A|B) = \frac{Pr(A \cap B)}{Pr(B)}
\end{aligned}
\end{equation}
이를 통해 두 사건이 동시에 발생한 확률은 $Pr(A \cap B) = Pr(A)Pr(B|A)$와 같이 나타낼 수 있다. 이 때, $Pr(A \cap B) = Pr(B \cap A)$이므로 $A,B$ 순서를 바꿔도 공식이 성립한다. 이는 $A$가 발생했을 때 $B$가 발생할 확률을 의미한다.
\begin{equation}
\begin{aligned}
Pr(B|A) = \frac{Pr(B \cap A)}{Pr(A)}
\end{aligned}
\end{equation}
만약 두 사건 $A,B$가 독립이면 조건부 확률은 다음과 같다.
\begin{equation}
\begin{aligned} Pr(A|B) = \frac{Pr(A \cap B)}{Pr(B)} = \frac{Pr(A)Pr(B)}{Pr(B)} = Pr(A)
\end{aligned}
\end{equation}
Bayesian rule
Bayesian rule은 다음과 같은 조건부확률 간 관계를 의미한다.
\begin{equation}
\begin{aligned}
Pr(A|B) & = \frac{Pr(A \cap B)}{Pr(B)} \\ & = \frac{Pr(B|A)Pr(A)}{Pr(B)}
\end{aligned}
\end{equation}
- $Pr(A|B)$: posterior probability
- $Pr(B|A)$: likelihood
- $Pr(A)$: prior probability
Random variables
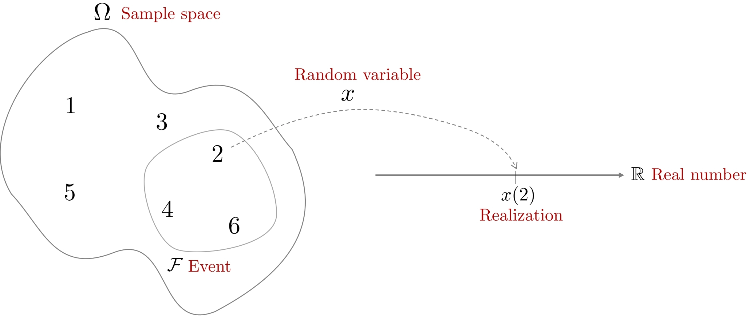
확률변수(random variable) $x$는 표본공간 $\Omega$에 정의된 함수를 의미한다. 이 함수는 확률공간 $(\Omega, \mathcal{F}, Pr)$의 한 원소를 Borel 가측공간 $(\mathbb{R}, \mathcal{B})$의 원소로 변환하는 역할을 수행한다.
\begin{equation}
\begin{aligned}
& \boxed{ x : \Omega \rightarrow \mathbb{R} } \\
&\text{ such that } \\
& \qquad \forall B \in \mathcal{B} \\
& \qquad x^{-1}(B) \in \mathcal{F}
\end{aligned}
\end{equation}
- Borel 가측공간(mesurable space): 실수들의 집합으로 만들어진 공간을 Borel 가측공간이라고 하며 이 때 $\sigma$-field를 Borel set이라고 한다.
- 확률(probability)은 표본공간의 부분집합인 $\sigma$-field를 하나의 실수값으로 측정해주는 연산자(=measure)인 반면에, 확률변수(random variable)는 표본공간의 하나의 원소를 하나의 실수값으로 변환해주는 함수(=function)를 말한다. 즉, 확률과 달리 확률변수는 하나의 원소에 대해서만 변환이 가능하다.
- 확률변수가 함수라면 무엇이 무작위성(randomness)이 있다는 것일까? 표본공간 $\Omega$에서 하나의 원소를추출할 때 무작위로 하나를 선택한 후 하나의 실수값으로 변환하기 때문에 일반적으로 확률변수가 무작위성이 있다고 한다.
- 표본공간 $\Omega$의 하나의 원소 $w$가 있을 때 $x(w)$를 실현(realization)이라고 한다. 간단히 말하자면 샘플링을 의미한다(e.g., 가우시안 샘플링).
- $x$에 대한 모든 실현값들의 집합을 알파벳(alphabet of $x$)이라고 한다.
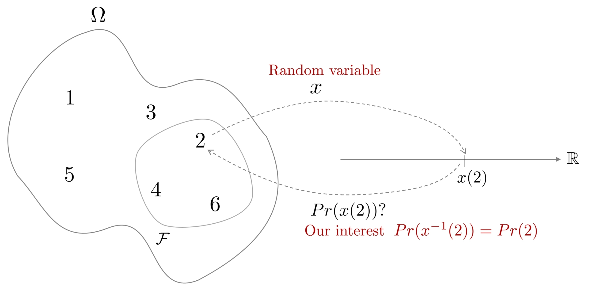
- 우리는 확률변수 $x$ 자체보다 $x$의 확률 $Pr(x)$에 관심이 있다. 실현값이 $x \in B, B \in \mathcal{B}$일 때 다음과 같이 정의한다.
- \begin{equation}
\begin{aligned}
Pr(x\in B) \triangleq Pr(x^{-1}(B)) = Pr(\{w : x(w) \in B \})
\end{aligned}
\end{equation}
- \begin{equation}
Discrete random variable
주사위 굴리기나 동전 던지기 같이 값이 유한하거나 셀 수 있는 무한의 값들을 가지는 확률변수를 이산확률변수라고 한다. 확률질량함수(probability mass function, pmf) $P(\cdot)$를 사용하여 각 값에 대한 확률을 나타내며 각각의 개별 값에 대해 명확한 확률을 할당할 수 있다.
Continuous random variable
온도 측정이나 물체의 길이 측정, 주식 가격 등 연속적인 범위의 값을 가지는 확률변수를 연속확률변수라고 한다. 확률밀도함수(probability density function, pdf) $p(\cdot)$을 사용하여 값의 범위에 대한 확률을 나타내며 개별 값에 대한 확률을 표현할 수 없으나 범위에 대한 확률을 표현할 수 있는 특징이 있다.
Probability distribution
확률분포(probability distribution)는 확률변수 $x$가 가질 수 있는 값들이 얼마나 자주 나타나는지(=확률 또는 밀도)를 정리한 것이다. 이산(discrete)인 경우에는 각 값에 확률질량함수(pmf) $P(x)$가 대응하고 연속(continuous)인 경우에는 확률밀도함수(pdf) $p(x)$가 대응한다. 단, 연속인 경우 $p(x)$는 한 점에서의 확률이 아니라 '밀도'이며 확률은 구간 적분으로 계산한다:
\begin{equation}
\begin{aligned}
Pr(a \le x \le b)=\int_a^b p(x)\,dx.
\end{aligned}
\end{equation}
Discrete probability distribution
Bernoulli distribution
확률 변수의 값이 성공 혹은 실패로 나타나는 경우의 확률 분포를 베르누이 분포라고 한다. 확률 실험의 결과 값이 성공 혹은 실패로 나타나는 실험을 베르누이 실험(Bernoulli experiment)라고 한다. 확률변수 $x$가 성공이면 $x=1$, 실패이면 $x=0$으로 정의하고 성공 확률을 $p$라 두면 다음과 같다:
\begin{equation}
\begin{aligned}
& P(x=0) = 1-p \\
& P(x=1) = p \\ \end{aligned}
\end{equation}
확률변수 $x$가 베르누이 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
& x \sim \text{Ber}(p)
\end{aligned}
\end{equation}
베르누이 분포의 pmf는 다음과 같다.
\begin{equation} \boxed{
\begin{aligned}
&P(x) = p^x (1-p)^{1-x} \quad x =0,1
\end{aligned} }
\end{equation}
베르누이 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = p\\
& \text{var}(x) = p(1-p)
\end{aligned} }
\end{equation}
Example : 동전이 앞면으로 나올 경우, 나오지 않을 경우($x \sim \text{Ber}(\frac{1}{2})$). 주사위를 던져서 3이 나올 확률과 나오지 않을 확률($x \sim \text{Ber}(\frac{1}{6})$)
Binomal distribution
이항 분포(binomial distribution)은 고정된 수의 독립적인 베르누이 실험에서 성공 횟수를 모델링하는 확률분포이다. 즉, 베르누이 시행을 여러 번 하는 것을 말한다. 예를 들어 10번의 동전 던지기에서 앞면이 나오는 횟수 등이 이에 해당한다. 확률변수 $x$가 이항 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \text{Bin}(n,p)
\end{aligned}
\end{equation}
이항 분포의 pmf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
P(x) = \ _{n}C_{r} p^r (1-p)^{n-r} \quad \text{ for } r =0,1,\cdots,n
\end{aligned} }
\end{equation}
- $n$: 시행 횟수
- $r$: 성공 횟수
- $p$: 각 시행에서 성공할 확률
이항 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = np\\
& \text{var}(x) = np(1-p)
\end{aligned} }
\end{equation}
Example : 주사위를 10번 던져서 숫자 3이 5번 나올 확률($x \sim \text{Bin}(10,\frac{1}{6}), r=5$)
Geometric distribution
기하 분포(geometric distribution)은 여러 베르누이 실험에서 첫 번째 성공이 나타날 때까지의 시행 횟수를 모델링하는 확률분포이다. 예를 들어 동전을 던져 처음으로 앞면이 나오기까지 걸린 횟수 등이 이에 해당한다. 확률변수 $x$가 기하 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \text{Geom}(p)
\end{aligned}
\end{equation}
기하 분포의 pmf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
P(x) = (1-p)^{x-1} p \quad \text{ for } x =1,2,\cdots
\end{aligned} }
\end{equation}
- $x$: 첫 번째 성공까지 시행 횟수
- $p$: 성공 확률
기하 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \frac{1}{p}\\
& \text{var}(x) = \frac{1-p}{p^2}
\end{aligned} }
\end{equation}
Example : 동전을 던졌을 때 처음 앞면이 나오기까지 걸린 횟수($x \sim \text{Geom}(\frac{1}{2})$). 연애에서 결혼까지 이어질 확률이 10%일 때 $x$번째 연애에 결혼할 확률($x \sim \text{Geom}(0.1)$)
Negative binomial distribution
음이항 분포(negative binomial distribution)은 성공 확률이 $p$인 베르누이 실험에서 실패가 $r$번 발생하기까지의 성공 횟수를 모델링하는 확률분포이다. 이는 기하 분포의 일반화된 형태로 볼 수 있으며 기하 분포가 첫 번째 성공까지의 시행 횟수를 모델링한다면 음이항 분포는 $x$번째 성공까지의 시행 횟수를 모델링한다. 예를 들어 생물학적 실험에서 목표 달성까지의 실패 횟수 분석 등에 사용된다. 확률변수 $x$가 음이항 분포를 따른다고 하면 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \text{NB}(r,p)
\end{aligned}
\end{equation}
음이항 분포의 pmf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
P(x) = \ _{x+r-1}C_x (1-p)^{r} p^x \quad \text{ for } x =0,1,2,\cdots
\end{aligned} }
\end{equation}
- $n$: 전체 시행 횟수. $n=x+r$
- $x$: 성공 횟수 (일반적으로 독립변수로 취급)
- $r$: 실패 횟수 (일반적으로 상수로 취급)
- $p$: 각 실험에서의 성공 확률
음이항 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \frac{pr}{1-p}\\
& \text{var}(x) = \frac{pr}{(1-p)^2}
\end{aligned} }
\end{equation}
Example : 포커 게임에서 이길 확률이 30%일 때 5번 패배할 때까지 발생한 승리가 $x$번일 확률($x \sim \text{NB}(5,0.3)$). 생물학적 실험 성공 확률이 10%일 때 3번 실패할 때까지 $x$번 성공했을 확률($x \sim \text{NB}(3,0.1)$)
Poisson distribution
포아송 분포(poisson distribution)은 이항분포에서 유도된 특수한 분포로써 단위 시간 또는 공간에서 발생하는 사건의 수를 모델링하는 확률분포이다. 예를 들어 한 시간 동안 상점에 들어오는 고객 수 등이 이에 해당한다. 확률변수 $x$가 포아송 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \text{Pois}(\lambda)
\end{aligned}
\end{equation}
포아송 분포의 pmf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
P(x) = \frac{\lambda^{x} e^{-\lambda}}{x!} \quad \text{ for } x =0,1,2,\cdots
\end{aligned} }
\end{equation}
- $x$: 발생한 사건의 수
- $\lambda$: 단위 시간/공간 당 평균 발생 횟수
포아송 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \lambda \\
& \text{var}(x) = \lambda
\end{aligned} }
\end{equation}
Example : 한 시간 동안 평균 10통의 전화가 온다고 할 때 실제 한 시간 동안 전화가 $x$통 올 확률 ($x \sim \text{Pois}(10)$). 도서관에 평균적으로 하루 200명의 방문객이 온다고 할 때, 특정 하루에 방문객이 $x$명일 확률($x \sim \text{Pois}(200)$)
Continuous probability distribution
Uniform distribution
균등분포(uniform distribution)이란 주어진 범위 내에서 모든 값이 동일한 확률로 발생하는 확률분포이다. 확률변수 $x$가 균등분포를 따른다고 하면 일반적으로 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \mathcal{U}(a,b)
\end{aligned}
\end{equation}
- $a,b$ 구간에서 확률변수가 균등분포를 따른다는 의미
균등분포의 pdf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
p(x) = \begin{cases}
\frac{1}{b-a} & \text{ for } a \leq x \leq b \\
0 & \text{ otherwise }
\end{cases}
\end{aligned} }
\end{equation}
균등 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \frac{a+b}{2} \\
& \text{var}(x) = \frac{(b-a)^2}{12}
\end{aligned} }
\end{equation}
Example : 0부터 1 사이에서 무작위로 실수를 하나 뽑을 때 그 값이 $x$일 확률($x \sim \mathcal{U}(0,1)$). 하루 24시간을 0시부터 24시 구간으로 정해놓고 무작위로 시간 한 점을 고른다면 그 점이 $x$시일 확률($x \sim \mathcal{U}(0,24)$)
Gaussian distribution
확률변수 $x$가 가우시안 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \mathcal{N}(\mu, \sigma^{2})
\end{aligned}
\end{equation}
- $x \sim \mathcal{N}(\mu, \sigma^2)$: 확률변수 $x$가 평균이 $\mu$이고 분산이 $\sigma^2$인 가우시안 분포를 따른다는 의미
가우시안 분포의 pdf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
p(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}}\exp \bigg(-\frac{1}{2\sigma^{2}}(\mathbf{x}-\mu)^{2} \bigg)
\end{aligned} }
\end{equation}
가우시안 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \mu \\
& \text{var}(x) = \sigma^2
\end{aligned} }
\end{equation}
가우시안 분포는 자연 및 과학, 공학계에서 매우 널리 사용되는 분포이며 정규 분포(normal distribution)라고도 불린다.
Example : 성인 남성의 몸무게를 평균 80kg, 표준편차 5kg으로 가정할 때 성인 남성 한 명의 몸무게가 $x$일 확률($x \sim \mathcal{N}(80, 5^{2})$). 어떤 측정기에서 발생하는 오차가 평균 0, 표준편차 1인 정규 분포를 따르는 경우 측정값이 $x$일 확률($x \sim \mathcal{N}(0, 1^{2})$)
Chi-square distribution
카이제곱(chi-square) 분포는 관측 데이터 $[x[1],x[2],\cdots,x[n]]^{\intercal}$가 서로 독립이며 동일한 분포를 갖고 있을 때(=i.i.d), 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
y = \sum_{i=1}^{n}x_i^2 \sim \mathcal{X}^2_n
\end{aligned}
\end{equation}
- $x_{i} \sim \mathcal{N}(0,1), \ i=1,2,\cdots,n$ : 평균이 0이고 분산이 1인 표준정규분포를 따른다
- $\mathcal{X}^2_n$: 자유도가 $n$인 카이스퀘어 분포
즉, 확률 변수 $x_{i}$의 제곱의 합은 카이제곱 분포를 따른다. 확률변수 $y$가 카이제곱 분포를 따른다고 하면 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
y \sim \chi^2(n)
\end{aligned}
\end{equation}
카이제곱 분포의 pdf는 다음과 같이 나타낼 수 있다.
\begin{equation} \boxed{
\begin{aligned}
p(y) = \begin{cases}
\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})} y^{\frac{n}{2}-1} \exp(-\frac{y}{2}) \quad & y \geq 0 \\
0 \quad & y < 0
\end{cases}
\end{aligned} }
\end{equation}
- $\Gamma(k) = \int_{0}^{\infty}x^{k-1}e^{-x}dx$: 감마 함수. 자연수 $n$에 대하여 $\Gamma(n) = (n-1)!$이 성립한다. 팩토리얼($!$)을 일반화한 함수로 생각하면 된다.
카이제곱 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(y) = n \\
& \text{var}(y) = 2n
\end{aligned} }
\end{equation}
Example : 음식점의 A,B,C 세 메뉴의 주문 비율이 예상 비율 (0.5, 0.3, 0.2)과 얼마나 다른지 알아보기 위해 카이제곱 적합도 검정을 실시해보자. 관측 비율과 예상 비율 비교해 구한 통계량 $y = \sum \frac{(Meas-Expect)^2}{Expect}$은 자유도($n-1, n=3$)를 갖는 $\chi^2$ 분포를 따른다($y \sim \chi^2(2)$). 통계량 $y$가 임계값 이하일 확률은 $\chi^2(2)$의 누적분포함수(CDF)로 구할 수 있다
온도 센서가 동일한 온도를 측정할 때 오차($x_1, \cdots, x_k$)가 서로 독립인 표준정규분포 $\mathcal{N}(0,1)$를 따른다고 가정하자. 이 때 8번 측정해서 나온 오차를 각각 제곱한 뒤 합을 구한 값 $y = x_1^2+x_2^2+\cdots +x_8^2$은 카이제곱 분포를 따른다. ($y \sim \chi^2(8)$). 오차의 제곱합 $y$가 특정 값 이하로 나올 확률은 $\chi^2(8)$ 분포의 누적분포함수(CDF)로 계산할 수 있다
Exponential distribution
지수 분포(exponential distribution)는 주로 '대기 시간'을 모델링하는데 사용된다. 예를 들어 웹사이트에 방문자가 도착하는 시간 등이 해당한다. 확률변수 $x$가 지수 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \text{Exp}(\lambda)
\end{aligned}
\end{equation}
지수 분포의 pdf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
p(x) = \lambda e^{-\lambda x} \quad \text{ for } x \geq 0, \lambda > 0
\end{aligned} }
\end{equation}
- $\lambda$: 단위 시간당 사건이 발생하는 평균 비율(또는 강도)를 말한다.
지수 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \frac{1}{\lambda} \\
& \text{var}(x) = \frac{1}{\lambda^2}
\end{aligned} }
\end{equation}
Example : 콜센터 전화가 걸려오기까지 평균 2분 걸린다면 대기 시간이 $x$분일 확률 ($x \sim \text{Exp}(\frac{1}{2})$). 어떤 부품이 평균 100시간 후 고장난다면 고장까지 걸리는 시간이 $x$시간일 확률($x \sim \text{Exp}(\frac{1}{100})$)
Gamma distribution
감마 분포(gamma distribution)는 지수 분포를 일반화한 것으로, 여러 지수적인 사건들의 합을 모델링한 확률분포이다. 예를 들어 특정 이벤트가 $n$번 발생하기까지의 대기 시간을 나타낼 수 있다. 확률변수 $x$가 감마 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \Gamma(k, \theta)
\end{aligned}
\end{equation}
감마 분포의 pdf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
p(x) = \frac{x^{k-1} e^{-x/\theta}}{\Gamma(k) \theta^k} \quad \text{ for } x > 0, k >0, \theta > 0
\end{aligned} }
\end{equation}
- $k$: 형상 파라미터(shape parameter)
- $\theta$: 스케일 파라미터(scale parameter)
- $\Gamma(k) = \int_{0}^{\infty}x^{k-1}e^{-x}dx$: 감마 함수. 자연수 $n$에 대하여 $\Gamma(n) = (n-1)!$이 성립한다. 팩토리얼($!$)을 일반화한 함수로 생각하면 된다.
$k$가 자연수일 때는 $n$번째 이벤트가 발생하기까지의 대기시간으로 해석할 수 있다.
감마 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = k\theta \\
& \text{var}(x) = k\theta^2
\end{aligned} }
\end{equation}
Example : 은행 창구에서 고객이 업무를 처리하기까지 3단계 과정을 거치고 각 단계의 평균 소요 시간이 10분($\lambda=\frac{1}{10}$)일 때 한 번의 업무 처리에 걸리는 총 시간이 $x$분일 확률($x \sim \Gamma(3, \frac{1}{10})$). 업무 처리 시간이 $x$분 이하가 될 확률은 $\Gamma(3, \frac{1}{10})$의 누적분포함수(CDF)로 계산할 수 있다.
어떤 기계 부품이 3단계 하위 부품이 순차적으로 고장이 나야 완전히 작동을 멈춘다고 가정하자. 각 하위 부품의 고장까지 걸리는 시간이 1000시간으로 동일하다면($\frac{1}{1000}$) 전체 기계가 고장나는 시간이 $x$ 시간일 확률($x \sim \Gamma(3, \frac{1}{1000})$). $x$ 시간 이하가 될 확률은 $\Gamma(3, \frac{1}{1000})$의 누적분포함수(CDF)로 구할 수 있다.
Beta distribution
베타 분포(beta distribution)은 $0$과 $1$사이의 값을 가지는 확률변수의 분포를 의미한다. 이 분포는 주로 비율이나 확률을 모델링할 때 사용된다. 예를 들어 제품의 양품률, 투표에서 특정 후보자를 선택할 확률 등이 있다. 확률변수 $x$가 베타 분포를 따르는 경우 다음과 같이 표기한다.
\begin{equation}
\begin{aligned}
x \sim \text{Beta}(\alpha, \beta)
\end{aligned}
\end{equation}
베타 분포의 pdf는 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
p(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} \quad \text{ for 0 < x < 1}
\end{aligned} }
\end{equation}
- $\alpha, \beta$: 형상 파라미터(shape parameter)
- $B(x,y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)} = \int^{1}_{0} t^{x-1}(1-t)^{y-1}dt$: 베타함수는 감마함수의 비율로 표현되는 함수이며 이항계수를(=$_nC_k$) 일반화한 함수로 볼 수 있다.
베타 분포의 기대값과 분산은 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
& \mathbb{E}(x) = \frac{\alpha}{\alpha+\beta} \\
& \text{var}(x) = \frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}
\end{aligned} }
\end{equation}
Example : 동전의 앞면이 나올 확률을 정교하게 구해보자. 우선 앞면이 나올 확률을 $\text{Beta}(\alpha, \beta)$와 같이 모델링한다. $\alpha$는 앞면, $\beta$는 뒷면이 나올 확률과 관련이 있으며 예를 들어 $\alpha=2, \beta=3$이면 $\frac{2}{2+3}=0.4$, 즉 40% 정도로 앞면이 나온다고 할 수 있다. 사전 정보가 없으므로 $\alpha=\beta=1$로 가정하여 $x \sim \text{Beta}(1,1) = \mathcal{U}(0,1)$로 실험을 시작한 후 실제로 동전을 여러 번 던지면서 $\alpha, \beta$ 값을 업데이트할 수 있다.
실험 결과 동전의 앞면이 나올 '진짜' 확률이 $\text{Beta}(2,3)$을 따른다고 가정할 때 이 확률이 $x$ 이하일 확률은$\text{Beta}(2,3)$의 누적분포함수 $CDF(x)$값으로 구할 수 있다
새로 출시한 제품이 시장에서 차지하는 점유율을 0과 1 사이의 확률 변수로 보고 그것을 베타 분포를 따른다고 가정할 수 있다. 실제 점유을 데이터를 토대로 $\alpha, \beta$ 값을 업데이트한다
업데이트 결과 신제품이 시장에서 차지하는 점유율이 $\text{Beta}(5,5)$의 분포를 따른다고 가정할 때 점유율이 $x$ 이하일 확률은 $\text{Beta}(5,5)$의 누적분포함수 $CDF(x)$의 값으로 구할 수 있다
Joint probability distribution
결합확률분포(joint probability distribution)란 두 확률변수 $x,y$의 공통 분포를 의미한다.
\begin{equation}
\begin{aligned}
& P(x,y) \quad \cdots \text{ for discrete r.v.} \\
& p(x,y) \quad \cdots \text{ for continuous r.v.}
\end{aligned}
\end{equation}
Marginal probability distribution
주변확률분포(marginal probability)는 여러 확률변수들 사이에서 한 확률변수의 행동만을 고려하는 것을 말한다. 예를 들어, 두 이산확률변수 $x$와 $y$가 있고, 이들의 결합확률분포(joint probability distribution)가 주어졌을 때, $x$의 주변확률분포는 $y$가 취할 수 있는 모든 값에 대해 $x$의 확률을 합하여 얻어진다. 이산확률변수를 보면 다음과 같다.
\begin{equation}
\begin{aligned}
P(x) = \sum_{y} P(x, y)
\end{aligned}
\end{equation}
연속확률변수로 나타내면 다음과 같다.
\begin{equation}
\begin{aligned}
p(x) = \int p(x,y) dy = \int p(x|y)p(y)dy
\end{aligned}
\end{equation}
Conditional probability distribution
조건부 확률분포(conditional probability distribution)은 두 확률변수 $x,y$에 대하여 $y$가 발생했을 때 $x$가 발생할 확률을 의미한다. 이산확률변수에 대한 조건부 확률분포는 다음과 같다.
\begin{equation}
\begin{aligned}
P(x|y) = \frac{P(x, y)}{P(y)}
\end{aligned}
\end{equation}
이를 통해 두 확률변수가 동시에 발생한 확률는 $P(x, y) = P(x)P(y|x)$와 같이 나타낼 수 있다. 이 때, $P(x, y) = P(y, x)$이므로 $x,y$ 순서를 바꿔도 공식이 성립한다. 이는 $x$가 발생했을 때 $y$가 발생할 확률분포를 의미한다.
\begin{equation}
\begin{aligned}
P(y|x) = \frac{P(y, x)}{P(x)}
\end{aligned}
\end{equation}
만약 두 확률변수 $x,y$가 독립이면 조건부 확률분포는 다음과 같다.
\begin{equation}
\begin{aligned}
P(x|y) = \frac{P(x, y)}{P(y)} = \frac{P(x)P(y)}{P(y)} = P(x)
\end{aligned}
\end{equation}
연속확률분포에 대한 조건부 확률분포은 다음과 같다. 연속확률변수가 주어졌을 때, $y$가 주어졌을 때 $x$가 발생할 확률분포는 다음과 같다.
\begin{equation}
\begin{aligned}
p(x|y) = \frac{p(x, y)}{p(y)}
\end{aligned}
\end{equation}
반대로 $x$가 주어졌을 때 $y$가 발생할 확률분포는 다음과 같다.
\begin{equation}
\begin{aligned}
p(y|x) = \frac{p(y, x)}{p(x)}
\end{aligned}
\end{equation}
이 때, $p(x, y)$와 $p(y, x)$는 동일하다.
Bayesian rule
Bayesian rule은 다음과 같은 조건부확률분포 사이의 관계를 의미한다.
\begin{equation}
\begin{aligned}
p(x|y) & = \frac{p(x, y)}{p(y)} \\ & = \frac{p(y|x)p(x)}{p(y)}
\end{aligned}
\end{equation}
- $p(x|y)$: posterior
- $p(y|x)$: likelihood
- $p(x)$: prior
예를 들어, 로봇의 위치를 $\mathbf{x}$, 로봇의 센서를 통해 관측한 값을 $\mathbf{z}$이라고 했을 때 주어진 관측 데이터를 바탕으로 현재 로봇이 $\mathbf{x}$에 위치할 확률 $p(\mathbf{x}|\mathbf{z})$는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
p(\mathbf{x}|\mathbf{z}) = \frac{p(\mathbf{z}|\mathbf{x})p(\mathbf{x})}{p(\mathbf{z})} = \eta \cdot p(\mathbf{z}|\mathbf{x})p(\mathbf{x})
\end{aligned}
\end{equation}
- $p(\mathbf{x}|\mathbf{z})$: 관측값 $\mathbf{z}$이 주어졌을 때 로봇이 $\mathbf{x}$에 위치할 확률 (posterior)
- $p(\mathbf{z}|\mathbf{x})$ : $\mathbf{x}$ 위치에서 관측값 $\mathbf{z}$가 나올 확률 (likelihood)
- $p(\mathbf{x})$: 로봇이 $\mathbf{x}$ 위치에 존재할 확률 (prior)
- $\eta = 1/p(\mathbf{z})$ : 전체 확률분포의 넓이가 1이 되어 확률분포의 정의를 유지시켜주는 normalization factor이다. 주로 $\eta$로 치환하여 표현한다.
Moment
모멘트(moment, 또는 적률)은 확률분포의 특징을 설명해주는 지표를 의미한다. 1차 적률은 확률분포의 평균(mean)을 의미하고 2차 적률은 분산(variance)를 의미하며 3차 적률은 왜도(skewness), 4차 적률은 첨도(kurtosis)를 의미한다. 왜도는 확률분포의 비대칭성을 나타내는 지표이고 첨도는 확률분포의 뾰족한 정도를 나타내는 지표이다.
\begin{equation}
\boxed{ \begin{aligned}
& \mu = \mathbb{E}(x) \quad & \cdots \text{1st moment } \\
& \sigma^2 = \text{var}(x) = \mathbb{E}((x-\mu)^2) \quad & \cdots \text{2nd moment } \\
& \text{skewness} = \frac{\mathbb{E}((x-\mu)^3)}{\sigma^3} \quad & \cdots \text{3rd moment } \\
& \text{kurtosis} = \frac{\mathbb{E}((x-\mu)^4)}{\sigma^4} \quad & \cdots \text{4th moment } \\
\end{aligned} }
\end{equation}
임의의 두 분포 $A,B$가 있을 때 두 분포가 같은지 판단하려면 일반적으로 두 분포의 모멘트가 같은지를 판단하면 된다.
Expectation
기대값(expectation, expected value) $\mathbb{E}$란 확률적 사건에 대한 평균을 의미하며 사건이 벌어졌을 때 이득과 그 사건이 벌어질 확률을 곱한 것을 합한 값을 말한다. 표뵨공간 $\Omega$에서 정의된 확률변수 $x$가 있을 때 확률함수 $p$에 대한 $x$의 기대값은 $\mathbb{E}[x]$라고 하고 다음과 같은 식으로 나타낸다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbb{E}[x] = \sum_{x\in\Omega} x \cdot P(x)
\end{aligned} }
\end{equation}
위 식은 이산확률변수에 대한 기대값을 의미한다. 연속확률변수에 대한 기대값은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbb{E}[x] = \int_{-\infty}^{\infty} x \cdot p(x) dx
\end{aligned} }
\end{equation}
Properties of expectation
기대값은 선형성(Linearity)라는 성질을 가지고 있다. 수학에서 선형성에 대한 정의는 다음과 같다. 임의의 함수 f에 대해
- 임의의 수 x,y에 대해 f(x+y) = f(x)+f(y)가 항상 성립하고
- 임의의 수 x와 a에 대해 f(ax) = af(x)가 항상 성립하면
- 함수 f는 선형이라고 한다.
따라서 임의의 확률변수 $x,y$와 임의의 실수 $a,b$에 대해서 다음 식이 성립하게 된다.
\begin{equation}
\begin{aligned}
\mathbb{E}[ax+by] = a\mathbb{E}[x] + b\mathbb{E}[y]
\end{aligned}
\end{equation}
그리고 선형인 함수 $L(x)$에 대해서 기대값과 함수의 계산순서를 바꿀 수 있다.
\begin{equation}
\begin{aligned}
\mathbb{E}[L(x)] = L(\mathbb{E}[x])
\end{aligned}
\end{equation}
Conditional expectation
연속확률변수 $x$에 대한 기대값 $\mathbb{E}(x) = \int x p(x) dx$는 하나의 결정된 값을 의미하며 더 이상 확률성을 띄고 있지 않다. 하지만 두 확률변수 $x,y$의 조건부 기대값 $\mathbb{E}(x|y)$는 기대값을 취하더라도 여전히 $y$에 대한 확률변수가 되며 이 부분이 기대값과 가장 다른 부분이다.
Law of total expectation
확률 변수 $x,y$가 주어졌을 때 총 기대값의 법칙(law of total expectation)은 다음과 같이 정의한다.
\begin{equation}
\begin{aligned}
\mathbb{E}[x] = \mathbb{E}[\mathbb{E}[x|y]]
\end{aligned}
\end{equation}
자세히 표현하면 아래와 같다.
\begin{equation}
\begin{aligned}
\mathbb{E}_{x}[x] = \mathbb{E}_{y}[\mathbb{E}_{x}[x|y]]
\end{aligned}
\end{equation}
- $\mathbb{E}_{x}$: 확률 변수 $x$에 대한 기대값
- $\mathbb{E}_{y}$: 확률 변수 $y$에 대한 기대값
두 연속확률변수 $x,y$에 대하여 증명은 다음과 같이 할 수 있다.
\begin{equation}
\begin{aligned}
\mathbb{E}_{y}[\mathbb{E}_{x}[x|y]] & = \int \bigg( \int x p(x|y) dx \bigg) p(y) dy \\
& = \int \int x p(x|y) p(y) dx dy \\
& = \int \int x p(x,y) dx dy \\
& = \int x \bigg( \int p(x,y)dy \bigg) dx \\
& = \int x p(x) dx \\
& = \mathbb{E}_{x}[x]
\end{aligned}
\end{equation}
Variance and standard deviation
확률변수 $x$의 분산(variance)은 $\sigma^{2}$ 또는 var$[x]$라고 표기하고 다음과 같이 정의한다
\begin{equation}
\boxed{ \begin{aligned}
\text{var}[x] &= \mathbb{E}[(x-\mathbb{E}(x))^{2}] \\
\end{aligned} }
\end{equation}
또한 아래와 같이 표현할 수도 있다.
\begin{equation}
\begin{aligned}
\text{var}[x] & = \mathbb{E}[x^{2}] - (\mathbb{E}[x])^{2}
\end{aligned}
\end{equation}
분산의 제곱근을 표준편차(standard deviation)이라고 하며 $\sigma$로 표기한다.
Covariance and correlation
두 확률변수 $x,y$가 주어졌을 때 공분산(covarinace)이란 두 분포가 어떤 상관관계를 가지는지 나타내는 값을 말한다.
\begin{equation}
\boxed{ \begin{aligned}
\text{cov}(x,y) = \mathbb{E}[ (x-\mathbb{E}(x))(y-\mathbb{E}(y))]
\end{aligned} }
\end{equation}
이를 전개해보면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{cov}(x,y) & = \mathbb{E}[ (x-\mathbb{E}(x))(y-\mathbb{E}(y))] \\
& = \mathbb{E}[ xy -\mathbb{E}(x) y - \mathbb{E}(y) x + \mathbb{E}(x)\mathbb{E}(y) ] \\
& = \mathbb{E}(xy) -\mathbb{E}(y) \mathbb{E}(x) - \mathbb{E}(x) \mathbb{E}(y) + \mathbb{E}(x)\mathbb{E}(y) \\
& = \mathbb{E}(xy) - \mathbb{E}(x)\mathbb{E}(y)
\end{aligned}
\end{equation}
- $\text{cov}(x,y) > 0$: 두 확률변수가 양의 상관관계를 갖는다.
- $\text{cov}(x,y) < 0$ : 두 확률변수가 음의 상관관계를 갖는다.
- $\text{cov}(x,y) = 0$ : 두 확률변수의 상관관계가 없다(uncorrelated).
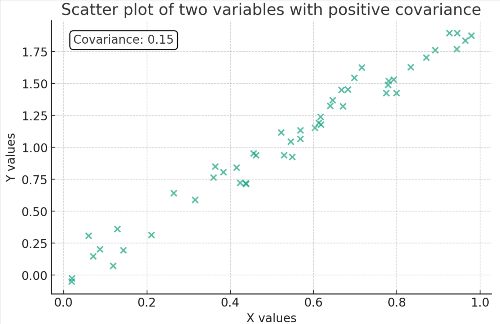
만약 두 확률변수가 상관관계가 없거나(uncorrelated) $x,y$가 독립(independence)이라면 $\mathbb{E}(xy) = \mathbb{E}(x)\mathbb{E}(y)$가 되어 $\text{cov}(x,y)=0$이 된다. 따라서 두 개념이 동일하다고 생각할 수 있으나 둘은 다른 개념이다. 두 확률변수가 상관관계가 없다고 하더라도(uncorrelated) 두 확률변수는 독립(independence)이 아닐 수 있다. 상관관계가 없다는 말은 선형 상관관계가 없다는 의미이므로 비선형적으로 상관관계가 있을 수 있음을 암시한다. 따라서 독립성의 개념이 조금 더 강한 개념으로 서로의 확률에 어떠한 영향도 주지 않음을 의미한다. 이 둘의 관계를 헷갈리지 않도록 유의한다.
\begin{equation}
\begin{aligned}
& \text{independence } \Rightarrow \text{ uncorrelated} \\
& \text{uncorrelated } \not\Rightarrow \text{ independence} \\
\end{aligned}
\end{equation}
Correlation coefficient
상관계수 $\rho_{xy}$는 공분산이 단위의 영향을 받는 점을 고려하여 이를 정규화한 값을 말한다.
\begin{equation}
\begin{aligned}
\rho_{xy} = \frac{\text{cov}(x,y)}{\sigma_x \sigma_y}
\end{aligned}
\end{equation}
상관계수는 $-1 \leq \rho_{xy} \leq 1$의 범위를 갖는다.
Orthogonal
두 확률변수 $x,y$가 직교한다(orhtogonal)는 의미는 두 확률변수의 곱의 기대값이 $0$임을 의미한다.
\begin{equation}
\begin{aligned}
\mathbb{E}(xy) = 0
\end{aligned}
\end{equation}
More on Gaussian distribution
Central limit theorem

중심극한정리(central limit theorem)은 무작위로 추출된 표본의 크기가 커질수록 표본 평균의 분포는 모집단의 분포 모양과는 관계없이 정규분포 가까워진다는 정리이다. 임의의 분포를 갖는 확률변수 $x_1, x_2, \cdots, x_n$들이 서로 독립이면서 동일한 분포를 갖고 있다고 하자(=i.i.d). 이들의 평균을 $\mathbb{E}(x_i) = \mu$, 분산을 $\text{var}(x_i)=\sigma^2$라고 했을 때 $\mathbf{x} = [x_1, x_2, \cdots, x_n]^{\intercal}$은 $n$이 커질수록 다음과 같은 표준정규분포로 수렴하게 된다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\mathbf{x}- n\mu}{\sigma \sqrt{n}} \sim \mathcal{N}(0,1)
\end{aligned} }
\end{equation}
Multivariate gaussian distribution
벡터 확률변수 $\mathbf{x} \in \mathbb{R}^{n}$가 가우시안 분포를 따른다고 하자.
\begin{equation}
\begin{aligned}
\mathbf{x} \sim \mathcal{N}(\mathbb{E}(\mathbf{x}), \mathbf{C})
\end{aligned}
\end{equation}
평균 $\mathbb{E}(\mathbf{x})$은 벡터이고 공분산 $\mathbf{C}$는 행렬이다.
\begin{equation}
\begin{aligned}
\mathbb{E}(\mathbf{x}) = \begin{bmatrix}
\mathbb{E}(x_1) \\ \mathbb{E}(x_2) \\ \vdots \\ \mathbb{E}(x_n)
\end{bmatrix} \in \mathbb{R}^{n} \qquad \mathbf{C} = \begin{bmatrix}
\mathbf{C}_{x_1 x_1} & \mathbf{C}_{x_1 x_2} & \cdots & \mathbf{C}_{x_1 x_n} \\
\mathbf{C}_{x_2 x_1} & \mathbf{C}_{x_2 x_2} & \cdots & \mathbf{C}_{x_2 x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\mathbf{C}_{x_n x_1} & \mathbf{C}_{x_n x_2} & \cdots & \mathbf{C}_{x_n x_n} \\
\end{bmatrix} \in \mathbb{R}^{n \times n}
\end{aligned}
\end{equation}
- $\mathbf{C}_{x_i x_j}=\text{cov}(x_i,x_j)
=\mathbb{E}\left[(x_i-\mathbb{E}(x_i))(x_j-\mathbb{E}(x_j))\right]$
pdf $p(\mathbf{x})$는 다음과 같이 정의된다.
\begin{equation} \boxed{
\begin{aligned}
p(\mathbf{x})=\frac{1}{(2\pi)^{\frac{n}{2}}\text{det}^{\frac{1}{2}}(\mathbf{C})}
\exp\left(-\frac{1}{2}({\mathbf{x}}-\mathbb{E}(\mathbf{x}))^{\intercal} \mathbf{C}^{-1} ({\mathbf{x}}-\mathbb{E}(\mathbf{x}))
\right)
\end{aligned} }
\end{equation}
- $\text{det}(\mathbf{C})$: $\mathbf{C}$의 행렬식(determinant)
- $\mathbf{C}^{-1}$ : information matrix $\boldsymbol{\Omega}$라고도 표현한다.
공분산 행렬에서 대각 성분들은 하나의 변수에 대한 분산을 의미하며 대각성분이 아닌 성분들은 두 변수 간 상관 관계를 의미한다.
Joint gaussian distribution
가우시안 분포를 따르는 두 벡터 확률변수 $\mathbf{x} \in \mathbb{R}^{n}$이고 $\mathbf{y} \in \mathbb{R}^{m}$가 주어졌을 때 결합확률분포(joint probability distribtuion)는 다음과 같이 나타낼 수 있다.
\begin{equation} \boxed{
\begin{aligned}
p(\mathbf{x},\mathbf{y}) = \frac{1}{(2\pi)^{\frac{n+m}{2}}\text{det}^{\frac{1}{2}}(\mathbf{C})}\exp \Bigg( -\frac{1}{2}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg)^{\intercal}\mathbf{C}^{-1}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg) \Bigg)
\end{aligned} }
\end{equation}
평균 벡터는 $\begin{bmatrix} \mathbb{E}(\mathbf{x})^{\intercal} & \mathbb{E}(\mathbf{y})^{\intercal} \end{bmatrix}^{\intercal} \in \mathbb{R}^{n+ m}$이고 공분산 행렬은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{C} = \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{bmatrix} = \begin{bmatrix}
n\times n & n\times m \\ m\times n & m\times m
\end{bmatrix} \in \mathbb{R}^{(n+m)\times (n+m)}
\end{aligned}
\end{equation}
Conditional gaussian distribution
가우시안 분포를 따르는 두 벡터 확률변수 $\mathbf{x}, \mathbf{y}$가 주어졌을 때 이들의 조건부 확률분포 $p(\mathbf{y}|\mathbf{x})$는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
p(\mathbf{y}| \mathbf{x}) & = \frac{p(\mathbf{x},\mathbf{y})}{p(\mathbf{x})} = \frac{p(\mathbf{x} | \mathbf{y})p(\mathbf{y})}{p(\mathbf{x})} = \eta \cdot p(\mathbf{x}|\mathbf{y})p(\mathbf{y}) \\
& \sim \mathcal{N}(\mathbb{E}(\mathbf{y}|\mathbf{x}), \mathbf{C}_{y|x})
\end{aligned}
\end{equation}
가 된다. 평균 $\mathbb{E}(\mathbf{y}|\mathbf{x})$과 분산 $\mathbf{C}_{y|x}$은 아래와 같다.
\begin{equation}
\boxed{ \begin{aligned}
& \mathbb{E}(\mathbf{y}|\mathbf{x})= \mathbb{E}(\mathbf{y}) + \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x})) \\
& \mathbf{C}_{y|x} = \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{yx}^{\intercal}
\end{aligned} }
\end{equation}
위 공분산 식을 자세히 보면 확률분포 $\mathbf{y}$는 조건부 확률분포 $p(\mathbf{y}| \mathbf{x})$를 구하기 전의 분산 $\mathbf{C}_{yy}$보다 반드시 같거나 작아지게 된다. 이는 prior $\mathbf{y}$에 추가적으로 $\mathbf{x}$라는 정보가 주어졌으므로(=given $\mathbf{x}$) 불확실성이 이전보다 작아진 것으로 해석할 수 있다.
Derivation of conditional gaussian distribution
\begin{equation} \label{eq:prob1}
\begin{aligned}
p(\mathbf{y}|\mathbf{x}) & = \frac{p(\mathbf{x},\mathbf{y})}{p(\mathbf{x})}\\
& = \frac{ \frac{1}{(2\pi)^{\frac{n+m}{2}}\text{det}^{\frac{1}{2}}(\mathbf{C})}\exp \Bigg( -\frac{1}{2}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg)^{\intercal}\mathbf{C}^{-1}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg) \Bigg) }{
\frac{1}{(2\pi)^{\frac{n}{2}}\text{det}^{\frac{1}{2}}(\mathbf{C}_{xx})}
\exp \bigg( -\frac{1}{2}({\mathbf{x}}-\mathbb{E}(\mathbf{x}))^{\intercal} \mathbf{C}_{xx}^{-1} ({\mathbf{x}}-\mathbb{E}(\mathbf{x})) \bigg)
}
\end{aligned}
\end{equation}
우선 $\exp(\cdot)$ 밖에 있는 행렬식(determinant)부터 살펴보자. 공분산 행렬 ${\color{Mahogany} \mathbf{C} = \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{bmatrix} }$는 matrix inversion lemma에 의해 다음과 같이 행렬 곱의 일부분으로 해석할 수 있다.
\begin{equation} \label{eq:prob2}
\begin{aligned}
\begin{bmatrix} \mathbf{I} & 0 \\ -\mathbf{C}_{yx}\mathbf{C}_{xx}^{-1} & \mathbf{I} \end{bmatrix} {\color{Mahogany} \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{bmatrix} } \begin{bmatrix} \mathbf{I} & -\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy} \\ 0 & \mathbf{I} \end{bmatrix} = \begin{bmatrix}
\mathbf{C}_{xx} & 0 \\ 0 & \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}
\end{bmatrix}
\end{aligned}
\end{equation}
- $\mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}$: Schur complement of $\mathbf{C}$ w.r.t. $\mathbf{C}_{xx}$이라고 한다.
임의의 블록 행렬 $\mathbf{A}$가 상삼각(upper-triangle), 하삼각(lower-triangle) 또는 대각(diagonal)일 경우 행렬식은 다음과 같이 나타낼 수 있다.
\begin{equation} \begin{aligned} \mathbf{A} = \begin{bmatrix} \mathbf{A}_{11} & \mathbf{A}_{12} \\ 0 & \mathbf{A}_{22} \end{bmatrix} \end{aligned} \end{equation}
- $\text{det}(\mathbf{A}) = \text{det}(\mathbf{A}_{11}) \text{det}(\mathbf{A}_{22})$
공분산 행렬 ${\color{Mahogany} \mathbf{C}}$는 다음과 같이 블록 삼각 행렬의 곱으로 LU 분해할 수 있다.
\begin{equation} \begin{aligned} {\color{Mahogany} \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{bmatrix} } = \begin{bmatrix} \mathbf{I} & 0 \\ \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1} & \mathbf{I} \end{bmatrix} \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ 0 & \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy} \end{bmatrix} \end{aligned} \end{equation}
따라서 ${\color{Mahogany} \mathbf{C}}$의 행렬식 $\text{det}({\color{Mahogany} \mathbf{C}})$은 다음과 같이 나타낼 수 있다.
\begin{equation} \begin{aligned} \text{det}({\color{Mahogany} \mathbf{C}}) & = \text{det}(\mathbf{I})\text{det}(\mathbf{I})\text{det}(\mathbf{C}_{xx})\text{det}(\mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}) \\ & = \text{det}(\mathbf{C}_{xx})\text{det}(\mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}) \end{aligned} \end{equation}
(\ref{eq:prob2}) 식을 보면 ${\color{Mahogany} \mathbf{C}}$를 제외하고 모두 대각 또는 삼각행렬이므로 블록 행렬의 행렬식 특성을 사용하여 행렬식을 구할 수 있다.
블록 행렬의 행렬식 특성을 이용하여 $\mathbf{B} = \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}$로 치환하고 행렬식을 다시 쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
& \text{det}(\mathbf{C}) = \text{det}(\mathbf{C}_{xx}) \text{det}(\mathbf{B}) \\
& \frac{\text{det}(\mathbf{C})}{\text{det}(\mathbf{C}_{xx})} = \text{det}(\mathbf{B})
\end{aligned}
\end{equation}
이를 (\ref{eq:prob1})는 대입한 후 전개하면 다음과 같다.
\begin{equation} \label{eq:prob3}
\begin{aligned}
p(\mathbf{y}|\mathbf{x}) & = \frac{1}{(2\pi)^{\frac{m}{2}}\text{det}^{\frac{1}{2}}({\color{Mahogany} \mathbf{B} })}
\exp \bigg( -\frac{1}{2} \bigg[ \bigg( \begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg)^{\intercal}\mathbf{C}^{-1}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg) \\
& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad- ({\mathbf{x}}-\mathbb{E}(\mathbf{x}))^{\intercal} \mathbf{C}_{xx}^{-1} ({\mathbf{x}}-\mathbb{E}(\mathbf{x})) \bigg] \bigg)
\end{aligned}
\end{equation}
(\ref{eq:prob2})에서 $\mathbf{C}^{-1}$은 다음과 같이 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{C}^{-1} =
\begin{bmatrix} \mathbf{I} & -\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy} \\ 0 & \mathbf{I} \end{bmatrix} \begin{bmatrix}
\mathbf{C}_{xx}^{-1} & 0 \\ 0 & \mathbf{B}^{-1}
\end{bmatrix} \begin{bmatrix} \mathbf{I} & 0 \\ -\mathbf{C}_{yx}\mathbf{C}_{xx}^{-1} & \mathbf{I} \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathbf{ABC}=\mathbf{D} \Rightarrow \mathbf{B}^{-1} = \mathbf{C}\mathbf{D}^{-1}\mathbf{A}$
$\mathbf{C}^{-1}$을 (\ref{eq:prob3})의 지수 부분에 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \begin{bmatrix} \tilde{\mathbf{x}}\\ \tilde{\mathbf{y}} \end{bmatrix}^{\intercal}{\color{Mahogany} \mathbf{C}^{-1}} \begin{bmatrix} \tilde{\mathbf{x}} \\ \tilde{\mathbf{y}} \end{bmatrix} - \tilde{\mathbf{x}}^{\intercal} \mathbf{C}_{xx}^{-1} \tilde{\mathbf{x}} \\
& \rightarrow \begin{bmatrix} \tilde{\mathbf{x}}\\ \tilde{\mathbf{y}} \end{bmatrix}^{\intercal} {\color{Mahogany} \begin{bmatrix} \mathbf{I} & -\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy} \\ 0 & \mathbf{I} \end{bmatrix} \begin{bmatrix}
\mathbf{C}_{xx}^{-1} & 0 \\ 0 & \mathbf{B}^{-1}
\end{bmatrix} \begin{bmatrix} \mathbf{I} & 0 \\ -\mathbf{C}_{yx}\mathbf{C}_{xx}^{-1} & \mathbf{I} \end{bmatrix} } \begin{bmatrix} \tilde{\mathbf{x}} \\ \tilde{\mathbf{y}} \end{bmatrix} - \tilde{\mathbf{x}}^{\intercal} \mathbf{C}_{xx}^{-1} \tilde{\mathbf{x}} \\
& = \begin{bmatrix} {\color{Cyan} \tilde{\mathbf{x}} } \\ \tilde{\mathbf{y}} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\tilde{\mathbf{x}} \end{bmatrix}^{\intercal} \begin{bmatrix}
{\color{Cyan} \mathbf{C}_{xx}^{-1} } & 0 \\ 0 & \mathbf{B}^{-1}
\end{bmatrix} \begin{bmatrix} {\color{Cyan} \tilde{\mathbf{x}} } \\ \tilde{\mathbf{y}} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\tilde{\mathbf{x}} \end{bmatrix} - {\color{Cyan} \tilde{\mathbf{x}}^{\intercal} \mathbf{C}_{xx}^{-1} \tilde{\mathbf{x}} } \\
& = ( \tilde{\mathbf{y}} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\tilde{\mathbf{x}})^{\intercal} \mathbf{B}^{-1}( \tilde{\mathbf{y}} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\tilde{\mathbf{x}}) \\
& = (\mathbf{y}- \underbrace{ (\mathbb{E}(\mathbf{y}) + \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\mathbf{x}-\mathbb{E}(\mathbf{x})) )}_{\mathbb{E}(\mathbf{y}|\mathbf{x})})^{\intercal} \underbrace{ [\mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}]}_{\mathbf{C}_{y|x}} (\mathbf{y}- \underbrace{ (\mathbb{E}(\mathbf{y}) + \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\mathbf{x}-\mathbb{E}(\mathbf{x})) )}_{\mathbb{E}(\mathbf{y}|\mathbf{x})})
\end{aligned}
\end{equation}
- $\tilde{\mathbf{x}} = \mathbf{x} - \mathbb{E}(\mathbf{x})$
- $\tilde{\mathbf{y}} = \mathbf{y} - \mathbb{E}(\mathbf{y})$
따라서 조건부 확률분포의 평균 $\mathbb{E}(\mathbf{y}|\mathbf{x})$과 분산 $\mathbf{C}_{y|x}$은 아래와 같다.
\begin{equation}
\boxed{ \begin{aligned}
& \mathbb{E}(\mathbf{y}|\mathbf{x})= \mathbb{E}(\mathbf{y}) + \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x})) \\
& \mathbf{C}_{y|x} = \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{yx}^{\intercal}
\end{aligned} }
\end{equation}
Linear transformation of Gaussian random variable
벡터 랜덤 변수 $\mathbf{x} \in \mathbb{R}^{n}$가 가우시안 분포를 따를 때는 다음과 같이 표기할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{x} \sim \mathcal{N}(\mathbb{E}(\mathbf{x}), \mathbf{C})
\end{aligned}
\end{equation}
만약 $\mathbf{x}$를 선형 변환(linear transformation)한 새로운 랜덤변수 $\mathbf{y} = \mathbf{Ax} + \mathbf{b}$가 주어졌다고 하면 $\mathbf{y}$는 아래와 같은 확률 분포를 따른다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{y} & = \mathbf{Ax} + \mathbf{b} \\
& \sim \mathcal{N}(\mathbf{A}\mathbb{E}(\mathbf{x}) + \mathbf{b}, \mathbf{A}\mathbf{C}\mathbf{A}^{\intercal})
\end{aligned} }
\end{equation}
공분산 $\text{cov}(\mathbf{Ax}+ \mathbf{b})$는 다음과 같이 유도할 수 있다.
\begin{equation}
\begin{aligned}
\text{cov}(\mathbf{Ax}+ \mathbf{b})
& = \mathbb{E}((\mathbf{y}-\mathbb{E}(\mathbf{y})(\mathbf{y}-\mathbb{E}(\mathbf{y})^{\intercal}) \\
&= \mathbb{E}((\mathbf{y}-(\mathbf{A}\mathbb{E}(\mathbf{x})+\mathbf{b}))(\mathbf{y}-(\mathbf{A}\mathbb{E}(\mathbf{x})+\mathbf{b}))^{\intercal}) \\
&= \mathbb{E}(((\mathbf{A}\mathbf{x}+\mathbf{b})-(\mathbf{A}\mathbb{E}(\mathbf{x})+\mathbf{b}))((\mathbf{A}\mathbf{x}+\mathbf{b})-(\mathbf{A}\mathbb{E}(\mathbf{x})+\mathbf{b}))^{\intercal}) \\
&= \mathbb{E}(\left [ \mathbf{A}(\mathbf{x}-\mathbb{E}(\mathbf{x})) \right ] \left [ \mathbf{A}(\mathbf{x}-\mathbb{E}(\mathbf{x})) \right ]^{\intercal}) \\
&= \mathbb{E}( \mathbf{A}(\mathbf{x}-\mathbb{E}(\mathbf{x}))(\mathbf{x}-\mathbb{E}(\mathbf{x}))^{\intercal} \mathbf{A}^{\intercal}) \\
&= \mathbf{A}\mathbb{E}((\mathbf{x}-\mathbb{E}(\mathbf{x}))(\mathbf{x}-\mathbb{E}(\mathbf{x}))^{\intercal})\mathbf{A}^{\intercal} \\
&= \mathbf{A} \mathbf{C} \mathbf{A}^{\intercal}
\end{aligned}
\end{equation}
스칼라 랜덤 변수 버전은 다음과 같이 나타낼 수 있다. 스칼라 랜덤 변수 $x\in \mathbb{R}$이 가우시안 분포를 따르는 경우 다음과 같이 표기할 수 있다
\begin{equation}
\begin{aligned}
x \sim \mathcal{N}(\mu, \sigma^2)
\end{aligned}
\end{equation}
$x$를 선형 변환한 새로운 랜덤 변수 $y = ax + b$가 주어졌다고 하면 $y$의 확률 분포는 다음과 같다
\begin{equation} \boxed{
\begin{aligned}
y & = ax + b \\
& \sim \mathcal{N}(a\mu + b , a^2\sigma^2)
\end{aligned} }
\end{equation}
Marginalization and conditioning is also gaussian
앞서 가우시안 분포를 따르는 두 벡터 확률변수 $\mathbf{x} \in \mathbb{R}^{n}$이고 $\mathbf{y} \in \mathbb{R}^{m}$가 주어졌을 때 결합확률분포(joint probability distribtuion)는 다음과 같이 나타낼 수 있다고 하였다.
\begin{equation} \boxed{
\begin{aligned}
p(\mathbf{x},\mathbf{y}) = \frac{1}{(2\pi)^{\frac{n+m}{2}}\text{det}^{\frac{1}{2}}(\mathbf{C})}\exp \Bigg( -\frac{1}{2}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg)^{\intercal}\mathbf{C}^{-1}\bigg(\begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}\bigg) \Bigg)
\end{aligned} }
\end{equation}
- $\mathbb{E}(\mathbf{x}, \mathbf{y}) = \begin{bmatrix} \mathbb{E}(\mathbf{x})^{\intercal} & \mathbb{E}(\mathbf{y})^{\intercal} \end{bmatrix}^{\intercal}$
- $\mathbf{C} = \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{bmatrix}$
이 때, 두 확률 변수 중 하나에 대한 주변확률분포(marginal distribution) 역시 가우시안 분포를 따른다.
\begin{equation}
\begin{aligned}
& p(\mathbf{x}) = \int p(\mathbf{x}, \mathbf{y}) d\mathbf{y} \sim \mathcal{N}(\mathbb{E}(\mathbf{x}), \mathbf{C}_{xx}) \\
& p(\mathbf{y}) = \int p(\mathbf{x}, \mathbf{y}) d\mathbf{x} \sim \mathcal{N}(\mathbb{E}(\mathbf{y}), \mathbf{C}_{yy})
\end{aligned}
\end{equation}
위 식에서 보다시피 $\mathbf{x}$의 주변확률분포 $p(\mathbf{x})$는 $\mathbf{y}$가 취할 수 있는 모든 값에 대하여 $\mathbf{x}$의 확률을 합하여 얻어지기 때문에 $\mathbf{y}$의 랜덤성이 사라지게 된다. 따라서 결합확률분포에서 $\mathbf{y}$와 관련된 부분은 사라지고 $\mathbf{x}$와 관련된 평균과 분산만이 살아남는다. $\mathbf{y}$의 주변확률분포 또한 마찬가지이다.
또한 두 확률 변수의 조건부 확률분포 $p(\mathbf{y}|\mathbf{x})$ 또는 $p(\mathbf{x}|\mathbf{y})$도 가우시안 분포를 따른다.
\begin{equation}
\begin{aligned}
& p(\mathbf{y}|\mathbf{x}) \sim \mathcal{N}(\mathbb{E}(\mathbf{y}|\mathbf{x}), \mathbf{C}_{y|x}) \\
& p(\mathbf{x}|\mathbf{y}) \sim \mathcal{N}(\mathbb{E}(\mathbf{x}|\mathbf{y}), \mathbf{C}_{x|y})
\end{aligned}
\end{equation}
- $\mathbb{E}(\mathbf{y}|\mathbf{x})= \mathbb{E}(\mathbf{y}) + \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x}))$
- $\mathbf{C}_{y|x} = \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{yx}^{\intercal}$
- $\mathbb{E}(\mathbf{x}|\mathbf{y})= \mathbb{E}(\mathbf{x}) + \mathbf{C}_{xy}\mathbf{C}_{yy}^{-1}(\mathbf{y} - \mathbb{E}(\mathbf{y}))$
- $\mathbf{C}_{x|y} = \mathbf{C}_{xx} - \mathbf{C}_{xy}\mathbf{C}_{yy}^{-1}\mathbf{C}_{xy}^{\intercal}$
조건부 확률분포에 대한 유도는 앞서 "Derivation of conditional gaussian distribution" 섹션에서 설명하였으므로 유도 과정이 궁금한 독자들은 해당 섹션을 참고하면 된다.
References
[1] (Blog)평균과 기댓값
[2] (Blog) PRLM - 4. The Exponential Family
[3] (Blog) [수리통계학] 38. 지수족
[4] (Wiki) Law of total expectation
[6] (Lecture) Bayesian Deep Learning - 최성준
[7] Williams, Christopher KI, and Carl Edward Rasmussen. Gaussian processes for machine learning. Vol. 2. No. 3. Cambridge, MA: MIT press, 2006.
[8] (Blog) [확률/통계] 확률분포 총 정리 (이산확률분포, 연속확률분포) - roytravel님 블로그
'Fundamental' 카테고리의 다른 글
| 추정 이론(Estimation Theory) 개념 정리 Part 1 - MVUE, CRLB (3) | 2024.02.10 |
|---|---|
| [Math] Useful Mathematical Identities and Tricks 정리 (2) | 2024.02.04 |
| [SLAM] Hand-eye Calibration 개념 정리 (+ Trajectory Evaluation) (3) | 2023.11.10 |
| 3D 강체 변환(Rigid Body Transformation) 개념 정리 (6) | 2023.01.24 |
| [SLAM] 에러와 자코비안 정리(Errors and Jacobians) 정리 Part 2 (3) | 2023.01.13 |
 A L I D A
A L I D A





