10. The Bayesian Philosophy
본 챕터에서는 지금까지 설명한 고전적인 추정 방법에서 벗어나 파라미터 $\theta$ 또한 하나의 확률 변수(random variable)로 보는 베이지안(Bayesian) 관점에 대하여 설명한다. 앞서 챕터 1에서 설명하였듯이 고전적인 관점과 베이지안 관점의 차이는 다음과 같다.
\begin{equation}
\begin{aligned}
& \text{Frequentist: } \quad \underbrace{x[n]}_{\text{r.v.}} = \underbrace{\theta}_{\text{deterministic}}+ w[n] \\
& \text{Bayesian: } \quad \underbrace{x[n]}_{\text{r.v.}} = \underbrace{\theta}_{\text{r.v.}} + w[n] \\
\end{aligned}
\end{equation}
- 고전적인 추정 방법 : 파라미터 $\theta$를 미지의 결정론적(deterministic) 파라미터로 보는 빈도주의(frequentist) 관점으로 해석
- 현대적인 추정 방법 : 파라미터 $\theta$를 별도의 확률 변수(random variable)로 보는하는 베이지안(bayesian) 관점으로 해석
베이지안 철학의 모티브는 다음과 같다.
- 만약 우리가 $\theta$에 대한 사전(prior) 정보를 알고 있다면 이는 더 나은 추정에 활용될 수 있다. 하지만 이를 위해서는 $\theta$에 대한 prior pdf가 미리 주어져 있거나 계산할 수 있어야 한다.
- Bayesian 추정은 MVUE를 찾는 것이 불가능한 경우 사용하기 좋은 방법이다. 예를 들어 특정 불편추정값(unbiased estimator)의 분산이 다른 불편추정값들의 분산보다 일관되게 작지 않은 경우를 생각해보자. 이런 경우 고전적인 방법으로는 MVUE를 찾는 것이 불가능하므로 파라미터 $\theta$에 pdf를 적용함으로써 우리는 그 추정값 $\hat{\theta}$을 찾는 방법을 생각할 수 있다. $\hat{\theta}$가 다른 추정값들보다 평균제곱오차(MSE)가 작다면 이는 최적의 추정값이라고 결론지을 수 있다. 즉, 파라미터 $\theta$에 대한 확률적인 가정을 함으로써 차선의 추정값을 찾을 수 있는데 이러한 관점이 Bayesian 관점이다.
10.1. Prior Knowledge and Estimation
만약 파라미터에 대한 사전 지식(prior knowledge)이 주어졌다면 이는 더 정확한 추정값을 찾는데 활용할 수 있다. Example 3.1에서 파라미터 $A$에 대한 MVUE는 $\bar{x}$라고 하였다. 하지만 이는 파라미터 $A$ 를 $-\infty < A < \infty$에서 얻은 경우에 대해서만 참이다. 만약 $A$를 제한된 영역인 $-A_0 \leq A \leq A_0$에서 얻었다고 가정해보자. 이렇게 되면 정해진 영역 밖에서는 $\hat{A} = \bar{x}$로 보는 것이 부적절할 수 있다. 다음과 같은 잘린 영역의(truncated) 추정값을 사용하면 추정값의 성능을 향상시킬 수 있다.
\begin{equation}
\begin{aligned}
\breve{A} = \begin{cases}
-A_0 \quad \quad \cdots \bar{x} < -A_0 \\
\bar{x} \quad \quad \quad \cdots -A_0 \leq \bar{x} \leq A_0 \\
A_0 \quad \quad \cdots \bar{x} > A_0
\end{cases}
\end{aligned}
\end{equation}
위 추정값에 대한 pdf를 구해보면 다음과 같다.
\begin{equation}
\begin{aligned}
p_{\breve{A}}(\xi ; A) = & \ \text{Pr}\{ \bar{x} \leq -A_0 \}\delta(\xi + A_0) \\
& + p_{\hat{A}}(\xi;A)[u(\xi+A_0) -u(\xi-A_0)] \\
& + \text{Pr}\{ \bar{x} \geq A_0 \}\delta(\xi - A_0)
\end{aligned}
\end{equation}
- $u(x)$ : 단위 스텝(unit step) 함수

위 그림에서 보다시피 $\breve{A}$ 추정값은 편향되어 있다(biased). 두 추정값을 MSE를 통해 비교해보면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{mse}(\hat{A}) & = \ \int_{-\infty}^{\infty} (\xi-A)^2 p_{\hat{A}}(\xi;A) d\xi \\
& = \ \int_{-\infty}^{-A_0}(\xi-A)^2 p_{\hat{A}}(\xi;A) d\xi + \int_{-A_0}^{A_0}(\xi-A)^2 p_{\hat{A}}(\xi;A) d\xi \\
& \quad \quad + \int_{A_0}^{\infty}(\xi-A)^2 p_{\hat{A}}(\xi;A) d\xi \\
& \ > \int_{-\infty}^{-A_0}(-A_0-A)^2 p_{\hat{A}}(\xi;A) d\xi + \int_{-A_0}^{A_0}(\xi-A)^2 p_{\hat{A}}(\xi;A) d\xi \\
& \quad \quad + \int_{A_0}^{\infty}(A_0-A)^2 p_{\hat{A}}(\xi;A) d\xi \\
& = \ \text{mse}(\breve{A})
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
\text{mse}(\hat{A}) > \text{mse}(\breve{A})
\end{aligned} }
\end{equation}
따라서 truncated 추정값 $\breve{A}$가 평균 추정값 $\hat{A}$보다 MSE 측면에서 더 좋은 값인 것을 알 수 있다. 비록 $\hat{A}$는 여전히 MVUE이지만, 여기에 편향성(biased)이 추가된 $\breve{A}$를 사용하여 MSE를 더 줄일 수 있었다.
우리는 방금 $\breve{A}$와 같은 좋은 추정값을 얻었지만 몇몇 독자들은 여전히 $\breve{A}$보다 정확한 최적의 추정값이 존재하는지 궁금할 수있다. 베이지안 추정 방법으로 데이터 모델을 재구성해야만 이를 확인할 수 있다. $A$가 정해진 영역에서 부더 얻은 값이라는 것을 알기 때문에 파라미터 $A$을 해당 영역에서 랜덤으로 추출한 확률 변수(random variable)로 가정할 수 있다. 특정 분포를 설정한만한 가정이 없으므로 균일 분포(uniform distribution)이라고 가정하면 $A \sim \mathcal{U}[-A_0, A_0]$이 된다.
기존의 고전적인 추정 방법와 베이지안 추정 방법를 비교한 그림은 아래와 같다.
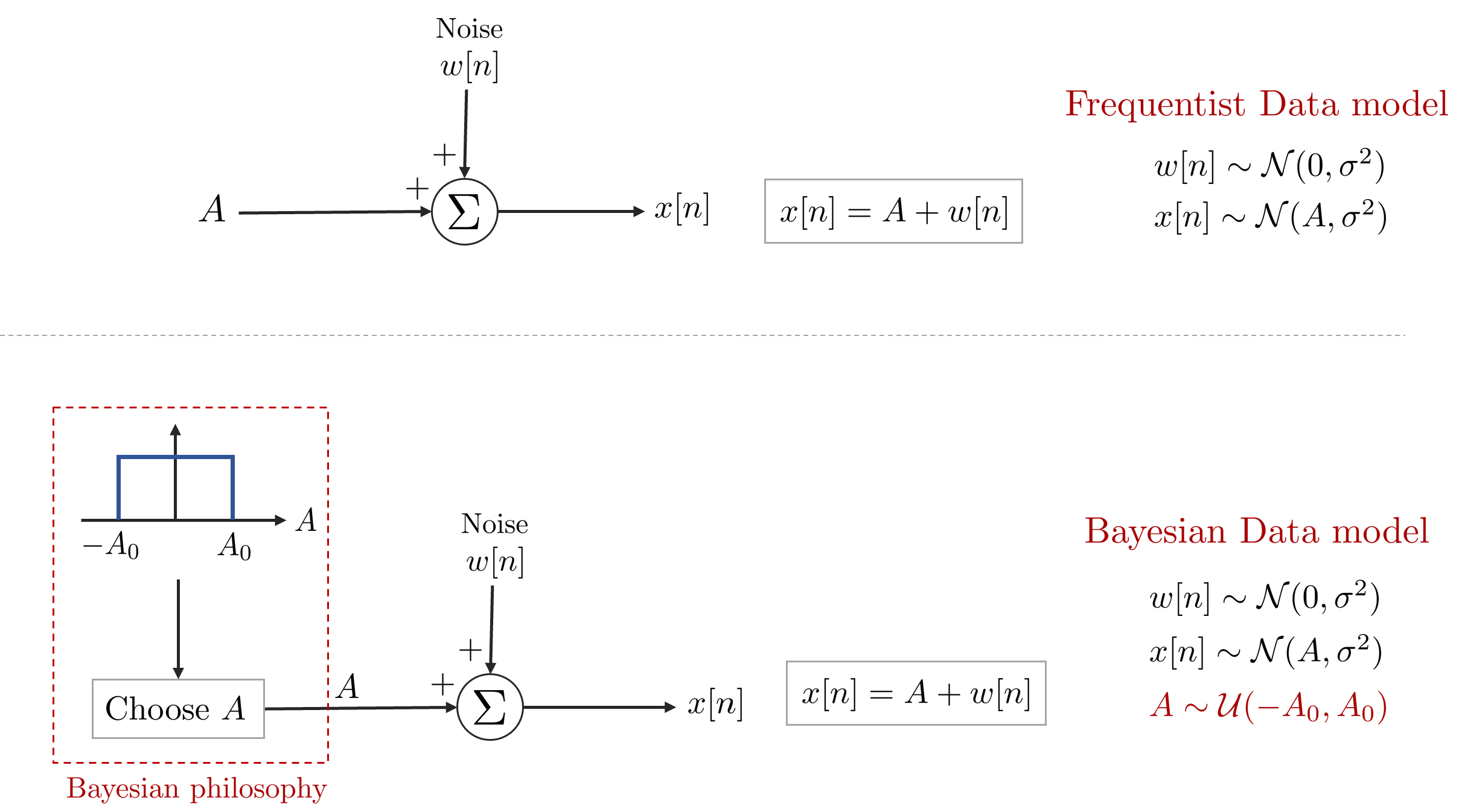
두 관점 모두 궁극적으로는 파라미터 $A$에 대한 최적의 추정값 $\hat{A}$을 얻는 것이 목표이지만 베이지안 추정 관점에서 봤을 때 $A$에 대한 사전 정보(prior knowledge)를 확인할 수 있게 되었다. 예를 들어 우리는 Bayesian MSE(=BMSE)를 최소화시키는 추정값 $\hat{A}$를 찾을 수 있다. BMSE는 다음과 같이 정의된다.
\begin{equation}
\boxed{ \begin{aligned}
\text{Bmse}(\hat{A}) = \mathbb{E}[(A-\hat{A})^2]
\end{aligned} }
\end{equation}
기존 MSE의 에러 $\hat{A}-A$와는 달리 BMSE에서는 에러를 $A-\hat{A}$로 정의하였다. 이러한 정의는 추후 베이지안 추정값에 대한 벡터 공간을 해석 할 때 유용하게 사용된다. 위 식에서 $A$는 고정된 값이 아닌 확률 변수(random variable)임에 유의하자. 따라서 기대값은 joint pdf $p(\mathbf{x}, A)$에 대한 기대값이 된다. 이는 근본적으로 기존 MSE와는 다른 관점이다.
\begin{equation}
\begin{aligned}
& \text{mse}(\hat{A}) = \int(\hat{A}-A)^2 p(\mathbf{x};A) d\mathbf{x} \\
& \text{Bmse}(\hat{A}) = \int\int (A-\hat{A})^2 p(\mathbf{x},A) d\mathbf{x}dA
\end{aligned}
\end{equation}
joint pdf는 $p(\mathbf{x}, A)=p(A|\mathbf{x})p(\mathbf{x})$와 같이 분리할 수 있으므로 위 식을 다시 쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
& \text{Bmse}(\hat{A}) = \int \bigg[\int (A-\hat{A})^2 p(A|\mathbf{x}) dA \bigg] p(\mathbf{x}) d\mathbf{x}
\end{aligned}
\end{equation}
확률의 정의에 의해 모든 $\mathbf{x}$에 대하여 $p(\mathbf{x})>0$이 성립한다. 따라서 위 브라켓 안에 있는 값만 작아진다면 BMSE는 최소화될 수 있다. 따라서 브라켓 안에 있는 식을 미분하면 다음과 같다.
\begin{equation}
\begin{aligned}
\frac{\partial }{\partial A} \int (A-\hat{A})^2 p(A|\mathbf{x}) dA & = \int \frac{\partial }{\partial A}(A-\hat{A})^2 p(A|\mathbf{x}) dA \\
& = \int -2(A-\hat{A}) p(A|\mathbf{x}) dA \\
& = -2\int A p(A|\mathbf{x}) dA + 2\hat{A} \underbrace{\int p(A|\mathbf{x}) dA}_{=1}
\end{aligned}
\end{equation}
위 식을 $0$으로 놓고 풀면 다음과 같은 추정값을 얻는다.
\begin{equation}
\begin{aligned}
\hat{A} & = \int Ap(A|\mathbf{x}) dA \\
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
\therefore \hat{A} & = \mathbb{E}(A|\mathbf{x})
\end{aligned} }
\end{equation}
따라서 BMSE에 대한 최적의 추정값 $\hat{A}$는 posterior pdf $p(A|\mathbf{x})$의 기대값인 것을 알 수 있으며 이를 MMSE(minimum MSE) 추정값이라고 부른다. Posterior pdf는 데이터 $\mathbf{x}$가 관찰되었을 때 파라미터 $A$의 pdf를 의미한다. 이와 대조적으로 prior pdf $p(A)$는 데이터가 관측되기 전 $A$의 pdf를 의미한다. 직관적으로 이해하자면 데이터를 관측하는 행동이 $A$의 pdf를 뾰족하게 만드는 효과를 가진다. 이는 데이터에 대한 지식이 $A$의 불확실성을 줄여주기 때문이다.

MMSE 추정값을 구하는 작업은 간단한 작업이 아니다. 우선 posterior pdf를 bayes rule을 통해 분해하는 것부터 시작하자.
\begin{equation} \label{eq:bay1}
\begin{aligned}
p(A|\mathbf{x}) & = \frac{p(\mathbf{x}|A)p(A)}{p(\mathbf{x})} \\
& = \frac{p(\mathbf{x}|A)p(A)}{\int p(\mathbf{x}|A)P(A)dA }
\end{aligned}
\end{equation}
위 식에서 분모는 파라미터 $A$와 무관하며 전체 확률의 크기를 정의에 따라 1로 만들어주는 정규화(normalization) 값이다. $p(A)$ 값은 앞서 균일 분포 $\mathcal{U}(-A_0, A_0)$를 따른다고 하였다. $p(\mathbf{x}|A)$는 $x[n]=A+w[n]$에서 $\mathbf{x}$의 pdf를 구하는 것과 동일하므로 아래와 같은 likelihood가 얻어진다.
\begin{equation}
\begin{aligned}
p(\mathbf{x}|\mathbf{A}) = \frac{1}{(2\pi\sigma^{2} )^{\frac{N}{2}} } \exp\bigg[ -\frac{1}{2\sigma^{2}} \sum_{n=0}^{N-1} (x[n] - A)^{2} \bigg]
\end{aligned}
\end{equation}
- $w[n] \sim \mathcal{N}(0, \sigma^2)$ : WGN
위 식은 이전 챕터에서 설명한 pdf $p(\mathbf{x};A)$와 동일한 것을 알 수 있다. 고전적인 추정 방법으로 해석할 때는 $p(\mathbf{x};A)$을 사용하는 것이 맞지만 베이지안 추정 방법에서 해석할 때는 $p(\mathbf{x}|A)$를 사용해야 한다. Prior와 likelihood를 (\ref{eq:bay1})에 대입하면 다음 식이 얻어진다.
\begin{equation} \label{eq:bay2}
\begin{aligned}
p(A|\mathbf{x}) = \begin{cases}
\frac{1}{c\sqrt{2\pi \frac{\sigma^2}{N}}}\exp\bigg[ -\frac{1}{2\frac{\sigma^2}{N}}(A-\bar{x})^2 \bigg] & \quad |A| \leq A_0 \\
0 & \quad |A| > A_0
\end{cases}
\end{aligned}
\end{equation}
$c$는 pdf의 크기를 $1$로 만들어주는 정규화 값이며 다음과 같다.
\begin{equation}
\begin{aligned}
c = \int_{-A_0}^{A_0} \frac{1}{2\pi\frac{\sigma^2}{N}}\exp\bigg[ -\frac{1}{2\frac{\sigma^2}{N}}(A-\bar{x})^2 \bigg]dA
\end{aligned}
\end{equation}
따라서 MMSE $\hat{A}$는 다음과 같이 구할 수 있다.
\begin{equation} \label{eq:bay3}
\boxed{ \begin{aligned}
\hat{A} & = \mathbb{E}(A|\mathbf{x}) \\
& = \int_{-\infty}^{\infty}Ap(A|\mathbf{x})dA \\
& = \frac{1}{c} \int_{-A_0}^{A_0} A \frac{1}{2\pi\frac{\sigma^2}{N}}\exp\bigg[ -\frac{1}{2\frac{\sigma^2}{N}}(A-\bar{x})^2 \bigg]dA
\end{aligned} }
\end{equation}
MMSE 추정값 $\hat{A}$은 비록 close form으로 구할 수는 없지만 적어도 $\hat{A}$가 $\bar{x},\sigma^2,A_0$에 관한 함수라는 것을 알 수 있다. $\hat{A}$ 값은 $A$에 대한 truncated 사전 분포 $p(A)$가 반영되었기 때문에 평균 $\bar{x}$의 값과 달리 편향되어 있다(biased). 하지만 데이터의 개수 $N$이 충분히 커진다면 posterior pdf $p(A|\mathbf{x})$는 점차 $\bar{x}$ 중심의 뾰족한 모양으로 변하며 가우시안에 근사하게 된다. 그렇게 되면 MMSE는 사전 분포의 영향을 점차 덜 받게 되어 MMSE는 $\bar{x}$에 근접하게 된다.

10.2. Choosing a Prior PDF
이전 섹션에서 보았듯이 한 번 prior pdf가 정해지면 MMSE는 (\ref{eq:bay1})을 통해 바로 구할 수 있다. 고전적인 방법에서는 MVUE를 구하는 closed form solution이 존재하는 반면 베이지안 추정 방법에서는 여전히 $p(A|\mathbf{x})$를 closed form solution으로 결정할수 있는지 여부가 걸림돌로 남아있다.
이전 예제에서는 (\ref{eq:bay2}) 식의 posterior pdf $p(A|\mathbf{x})$와 (\ref{eq:bay3}) 식의 posterior 평균의 값을 closef form으로 찾을 수 없었고 따라서 이런 상황에서는 MMSE 추정값을 찾기 위해서는 수치적분을 사용해야 한다. 실제 추정 문제에서는 $p(A|\mathbf{x})$를 closed form으로 찾는 것이 중요하기 때문에 이를 가능하게 해주는 prior pdf 선정 방법에 대해 설명한다.
10.2.1. Example 10.1 - DC Level in WGN - Gaussian Prior PDF
이전 예제에서 prior pdf를 아래와 같은 균일 분포(uniform distribution)으로 설정하였었다.
\begin{equation}
\begin{aligned}
p(A) = \begin{cases}
\frac{1}{2A_0} \quad & |A| \leq A_0 \\
0 \quad & |A| > A_0
\end{cases}
\end{aligned}
\end{equation}
이번에는 $p(A)$를 가우시안 분포를 가진다고 가정해보자.
\begin{equation}
\begin{aligned}
p(A) = \frac{1}{ \sqrt{ 2\pi\sigma_A^{2} }} \exp\bigg[ -\frac{1}{2\sigma_A^{2}} (x - \mu_A)^{2} \bigg]
\end{aligned}
\end{equation}
$A$에 대한 두 분포는 매우 다른 표현법을 가지는 것을 알 수 있다. 다음으로 likelihood는 다음과 같다.
\begin{equation}
\begin{aligned}
p(\mathbf{x}|\mathbf{A}) & = \frac{1}{(2\pi\sigma^{2} )^{\frac{N}{2}} } \exp\bigg[ -\frac{1}{2\sigma^{2}} \sum_{n=0}^{N-1} (x[n] - A)^{2} \bigg] \\
& = \frac{1}{(2\pi\sigma^{2} )^{\frac{N}{2}} } \exp\bigg[ -\frac{1}{2\sigma^{2}} \sum_{n=0}^{N-1}x^2[n] \bigg] \exp \bigg[ -\frac{1}{2\sigma^{2}}(NA^2 - 2NA\bar{x}) \bigg]
\end{aligned}
\end{equation}
따라서 posterior pdf $p(A|\mathbf{x})$는 다음과 같이 전개할 수 있다.
\begin{equation} \label{eq:bay4}
\begin{aligned}
p(A|\mathbf{x}) & = \frac{ {\color{Blue} p(\mathbf{x}|A) }{\color{Red} p(A) }}{\int {\color{Blue} p(\mathbf{x}|A) } {\color{Red} p(A) } dA } \\
& = \frac{ \frac{1}{ {\color{Blue} (2\pi\sigma^{2} )^{\frac{N}{2}} } {\color{Red} \sqrt{ 2\pi\sigma_A^{2} } }} {\color{Blue} \exp\bigg[ -\frac{1}{2\sigma^{2}} \sum_{n=0}^{N-1}x^2[n] \bigg] \exp \bigg[ -\frac{1}{2\sigma^{2}}(NA^2 - 2NA\bar{x} ) \bigg] } } { \int_{-\infty}^{\infty} \frac{1}{ {\color{Blue} (2\pi\sigma^{2} )^{\frac{N}{2}} } {\color{Red} \sqrt{ 2\pi\sigma_A^{2} } }} {\color{Blue} \exp\bigg[ -\frac{1}{2\sigma^{2}} \sum_{n=0}^{N-1}x^2[n] \bigg] \exp \bigg[ -\frac{1}{2\sigma^{2}}(NA^2 - 2NA\bar{x}) \bigg]} } \\
& \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \cdot \frac{ {\color{Red} \exp\bigg[ -\frac{1}{2\sigma_A^{2}} (x - \mu_A)^{2} \bigg] } }{ {\color{Red} \exp\bigg[ -\frac{1}{2\sigma_A^{2}} (x - \mu_A)^{2} \bigg] } dA } \\
& = \frac{ \exp\bigg[ -\frac{1}{2}\bigg( \frac{1}{\sigma^{2}} (NA^2-2NA\bar{x}) + \frac{1}{\sigma_A^2}(A-\mu_A)^2 \bigg) \bigg] } { \int_{-\infty}^{\infty} \exp\bigg[ -\frac{1}{2}\bigg( \frac{1}{\sigma^{2}} (NA^2-2NA\bar{x}) + \frac{1}{\sigma_A^2}(A-\mu_A)^2 \bigg) \bigg]dA } \\
& = \frac{\exp\bigg[ -\frac{1}{2}Q(A) \bigg]}{ \int_{-\infty}^{\infty} \exp\bigg[ -\frac{1}{2}Q(A) \bigg]dA}
\end{aligned}
\end{equation}
위 식의 분모는 정규화(normalization) 역할을 수행하기 때문에 $A$에 종속적이지 않은 것을 알 수 있다. 그리고 exponential 항 내부에 있는 $Q(A)$ 항은 $A$에 대한 2차식 형태(quadratic form)인 것을 알 수 있다. 따라서 prior pdf, likelihood가 모두 가우시안이면 posterior pdf 또한 $\mathbf{x}$에 대한 평균과 분산을 가지는 가우시안 분포임을 알 수 있다. $Q(A)$를 자세히 전개해보면 다음과 같다.
\begin{equation} \label{eq:bay5}
\begin{aligned}
Q(A) & = \frac{N}{\sigma^2}A^2 - \frac{2NA\bar{x}}{\sigma^2} + \frac{A^2}{\sigma_A^2} - \frac{2\mu_A A}{\sigma_A^2} + \frac{\mu_A^2}{\sigma_A^2} \\
& = \bigg( \frac{N}{\sigma^2}+\frac{1}{\sigma^2_A} \bigg)A^2 - 2\bigg( \frac{N}{\sigma^2}\bar{x} + \frac{\mu_A}{\sigma_A^2} \bigg)A + \frac{\mu_A^2}{\sigma_A^2}
\end{aligned}
\end{equation}
Posterior의 평균과 분산을 다음과 같이 정의하자.
\begin{equation}
\begin{aligned}
& \sigma_{A|x}^2 = \frac{1}{\frac{N}{\sigma^2}+\frac{1}{\sigma^2_A}} \\
& \mu_{A|x} = \bigg( \frac{N}{\sigma^2}\bar{x} + \frac{\mu_A}{\sigma_A^2} \bigg) \sigma_{A|x}^2
\end{aligned}
\end{equation}
(\ref{eq:bay5}) 식에 위를 대입하면 다음과 같은 2차식 형태로 변한다.
\begin{equation}
\begin{aligned}
Q(A) & = \frac{1}{\sigma_{A|x}^2} {\color{Mahogany} \big( A^2 -2\mu_{A|x}A + \mu_{A|x}^2 \big) } - \frac{\mu_{A|x}^2}{\sigma_{A|x}^2} + \frac{\mu_{A}^2}{\sigma_A^2} \\
& = \frac{1}{\sigma_{A|x}^2} {\color{Mahogany} \big( A^2 - \mu_{A|x}^2 \big)^2 } - \frac{\mu_{A|x}^2}{\sigma_{A|x}^2} + \frac{\mu_{A}^2}{\sigma_A^2}
\end{aligned}
\end{equation}
따라서 $p(A|\mathbf{x})$는 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
p(A|\mathbf{x}) & = \frac{ \exp\bigg[ -\frac{1}{2\sigma_{A|x}^2} \big( A^2 - \mu_{A|x}^2 \big)^2 \bigg] \exp\bigg[ -\frac{1}{2}\bigg( \frac{\mu_{A}^2}{\sigma_A^2} - \frac{\mu_{A|x}^2}{\sigma_{A|x}^2} \bigg) \bigg] }{ \int_{-\infty}^{\infty} \exp\bigg[ -\frac{1}{2\sigma_{A|x}^2} \big( A^2 - \mu_{A|x}^2 \big)^2 \bigg] \exp\bigg[ -\frac{1}{2}\bigg( \frac{\mu_{A}^2}{\sigma_A^2} - \frac{\mu_{A|x}^2}{\sigma_{A|x}^2} \bigg) \bigg] dA} \\
& = \frac{1}{ \sqrt{ 2\pi\sigma_{A|x}^{2} }} \exp\bigg[ -\frac{1}{2\sigma^2_{A|x}}(A-\mu_{A|x})^2 \bigg]
\end{aligned}
\end{equation}
앞서 언급한 것처럼 posterior pdf 또한 가우시안 분포를 가짐을 알 수 있다. MMSE 추정값을 구해보면 다음과 같다.
\begin{equation} \label{eq:bay9}
\boxed{ \begin{aligned}
\hat{A} & = \mathbb{E}(A|\mathbf{x}) \\
& = \mu_{A|x} \\
& = \frac{ \frac{N}{\sigma^2}\bar{x} + \frac{\mu_A}{\sigma_A^2} }{ \frac{N}{\sigma^2} + \frac{1}{\sigma^2_A } } \\
& = \frac{\sigma_A^2}{\sigma^2_A + \frac{\sigma^2}{N}}\bar{x} + \frac{\frac{\sigma^2}{N}}{\sigma^2_A + \frac{\sigma^2}{N}}\mu_A \\
& = \alpha \bar{x} + (1-\alpha) \mu_A
\end{aligned} }
\end{equation}
- $\alpha = \frac{\sigma_A^2}{\sigma^2_A + \frac{\sigma^2}{N}}$
$\alpha$는 $0 \leq \alpha \leq 1$의 값을 가지는 가중치 값이다. Prior pdf를 가우시안 분포로 가정하면 위와 같이 MMSE 추정값을 closed form으로 계산할 수 있다. MMSE 추정값 $\hat{A}$를 해석해보면 데이터가 거의 없는 경우 ($\sigma_A^2 \ll \sigma^2/N$), $\alpha$ 값은 작은 값을 가지며 $\hat{A} \approx \mu_A$가 되는 것을 알 수 있다. 하지만 데이터가 충분히 관측된 경우 ($\sigma_A^2 \gg \sigma^2/N$), $\alpha$ 값은 1에 근접하여 $\hat{A} \approx \bar{x}$가 됨을 알 수 있다. 이렇듯 가중치 값은 사전 지식의 신뢰도와 관측된 데이터 신뢰도 사이의 균형을 잡아주는 값이다. 아래 그림에서 보다시피 $N$ 값이 증가할수록 posterior pdf는 점점 뾰족해진다.

이러한 현상은 posterior pdf의 분산과 관련이 있다.
\begin{equation}
\boxed{ \begin{aligned}
\text{var}(A|\mathbf{x}) & = \sigma^2_{A|x} \\
& = \frac{1}{\frac{N}{\sigma^2} + \frac{1}{\sigma_A}}
\end{aligned} }
\end{equation}
위 식에서 보다시피 $N$이 커질수록 $\text{var}(A|\mathbf{x})$는 작아지는 것을 알 수 있다. 만약 prior pdf가 주어지지 않았다면 $\sigma_A^2 \rightarrow \infty$로 세팅한 것과 동일한 효과를 보이며 $\hat{A} \rightarrow \bar{x}$가 된다. 따라서 고전적인 추정 문제와 동일한 추정값을 얻게 된다.
마지막으로 앞서 주장했던 'prior pdf를 사용하면 더 좋은 추정값을 얻을 수 있다'는 사실을 증명해보자. BMSE를 다시 쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}) = \mathbb{E}[(A-\hat{A})^2]
\end{aligned}
\end{equation}
기대값의 정의에 따라 전개해보자.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}) & = \int\int (A-\hat{A})^2 p(\mathbf{x},A) d\mathbf{x}dA \\
& = \int\int (A-\hat{A})^2 p(A|\mathbf{x}) dA p(\mathbf{x}) d\mathbf{x} \\
\end{aligned}
\end{equation}
MMSE 추정값은 $\hat{A} = \mathbb{E}(A|\mathbf{x})$인 것을 알고 있으므로 이를 대입한다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}) & = \int {\color{Mahogany} \int (A- \mathbb{E}(A|\mathbf{x}))^2 p(A|\mathbf{x}) dA } p(\mathbf{x}) d\mathbf{x} \\
& = \int {\color{Mahogany} \text{var}(A|\mathbf{x}) } p(\mathbf{x}) d\mathbf{x}
\end{aligned}
\end{equation}
위 식에서 보다시피 BMSE는 posterior pdf의 분산이 $\mathbf{x}$의 확률 분포와 곱해진 값으로 해석할 수 있다. $\text{var}(A|\mathbf{x})$는 $\mathbf{x}$와 독립이므로 아래와 같이 쓸 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\text{Bmse}(\hat{A}) & = \int \sigma^2_{A|x} p(\mathbf{x}) d\mathbf{x} \\
& = \frac{1}{\frac{N}{\sigma^2} + \frac{1}{\sigma_A}} \\
& = \frac{\sigma^2}{N} \bigg( \frac{\sigma_A^2}{\sigma_A^2 + \frac{\sigma^2}{N}} \bigg) \\
& < \frac{\sigma^2}{N} \\
\end{aligned} }
\end{equation}
따라서 BMSE 값은 사전 지식(prior knowledge)가 없는 MMSE 값($\frac{\sigma^2}{N}$)보다 항상 작음을 알 수 있다($\sigma_A^2 \rightarrow \infty$ 경우 제외). 결론적으로 베이지안 추정 방법을 통해 prior pdf를 사용하면 항상 추정값의 성능을 향상시킬 수 있다.
10.3. Properties of the Gaussian PDF
이번 섹션에서는 다변량 가우시안 pdf의 성질을 자세히 알아보자. 우선 이변량 가우시안 분포 함수(bivariate Gaussian pdf)에 대해 먼저 알아 본 후 다변량 가우시안 분포 함수(multivariate Gaussian pdf)에 대해 순차적으로 알아본다.
두 가우시안 확률 변수(random variable) $[x, y]^{\intercal}$이 주어졌다고 하자. 두 확률 변수에 대한 결합 분포(joint pdf)는 다음과 같다.
\begin{equation} \label{eq:bay6}
\boxed{ \begin{aligned}
p(x,y) = \frac{1}{2\pi \det^{\frac{1}{2}}(\mathbf{C})} \exp\bigg[ -\frac{1}{2} \begin{bmatrix} x - \mathbb{E}(x) \\ y - \mathbb{E}(y) \end{bmatrix}^{\intercal}\mathbf{C}^{-1} \begin{bmatrix} x - \mathbb{E}(x) \\ y - \mathbb{E}(y) \end{bmatrix} \bigg]
\end{aligned} }
\end{equation}
위 식은 이변량 가우시안 분포라고도 불린다. 평균과 공분산은 다음과 같은 벡터의 형태를 띈다.
\begin{equation}
\begin{aligned}
& \mathbb{E}\bigg( \begin{bmatrix} x\\y \end{bmatrix} \bigg) = \begin{bmatrix} \mathbb{E}(x) \\ \mathbb{E}(y) \end{bmatrix} \\
& \mathbf{C} = \begin{bmatrix} \text{var}(x) & \text{cov}(x,y) \\
\text{cov}(y,x) & \text{var}(y) \end{bmatrix}
\end{aligned}
\end{equation}
$p(x), p(y)$의 주변 분포(marginal pdf) 또한 가우시안 분포가 된다. 이는 아래 식을 통해 알 수 있다.
\begin{equation}
\begin{aligned}
& p(x) = \int_{-\infty}^{\infty} p(x,y)dy = \frac{1}{\sqrt{2\pi\text{var}(x)}} \exp\bigg[ -\frac{1}{2\text{var}(x)} (x - \mathbb{E}(x))^2 \bigg]\\
& p(y) = \int_{-\infty}^{\infty} p(x,y)dy = \frac{1}{\sqrt{2\pi\text{var}(y)}} \exp\bigg[ -\frac{1}{2\text{var}(y)} (y - \mathbb{E}(y))^2 \bigg]
\end{aligned}
\end{equation}
$p(x,y)$의 공분산에 대한 타원형 등고선(contour)은 아래 값들이 변하지 않는 이상 일정한 값을 지닌다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} x - \mathbb{E}(x) \\ y - \mathbb{E}(y) \end{bmatrix}^{\intercal}\mathbf{C}^{-1} \begin{bmatrix} x - \mathbb{E}(x) \\ y - \mathbb{E}(y) \end{bmatrix}
\end{aligned}
\end{equation}
만약 $x_0$ 데이터가 관측되었다고 하면 $y$에 대한 조건부 확률은 다음과 같다.
\begin{equation}
\begin{aligned}
p(y|x_0) & = \frac{p(x_0,y)}{p(x_0)} \\
& = \frac{p(x_0,y)}{\int_{-\infty}^{\infty} p(x_0,y) dy}
\end{aligned}
\end{equation}

$y$에 대한 조건부 확률 $p(y|x_0)$는 분모항에 의해 정규화되어 크기가 1을 가진 가우시안 분포가 된다. 그리고 $p(x_0,y)$는 (\ref{eq:bay6}) 식에서 본 것처럼 $y$에 2차식 형태가 되므로 $y$에 대한 가우시안 분포를 가짐을 알 수 있다. 결론적으로 $p(x,y)$가 서로 결합 가우시안 분포를 이루는 경우(jointly gaussian) $p(y)$와 $p(y|x)$는 모두 가우시안 분포를 따르는 것을 알 수 있다. 보다 자세한 유도 과정은 Appendix 10A를 참조하면 된다.
10.3.1. Theorem 10.1 (Conditional PDF of Bivariate Gaussian)
두 확률 변수 $x,y$가 다음과 같은 평균과 공분산을 가지는 결합 분포를 가진다고 하자.
\begin{equation}
\begin{aligned}
p(x,y) = \frac{1}{2\pi \det^{\frac{1}{2}}(\mathbf{C})} \exp\bigg[ -\frac{1}{2} \begin{bmatrix} x - \mathbb{E}(x) \\ y - \mathbb{E}(y) \end{bmatrix}^{\intercal}\mathbf{C}^{-1} \begin{bmatrix} x - \mathbb{E}(x) \\ y - \mathbb{E}(y) \end{bmatrix} \bigg]
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \text{where, } \mathbb{E}\bigg( \begin{bmatrix} x\\y \end{bmatrix} \bigg) = \begin{bmatrix} \mathbb{E}(x) \\ \mathbb{E}(y) \end{bmatrix} \\
& \mathbf{C} = \begin{bmatrix} \text{var}(x) & \text{cov}(x,y) \\
\text{cov}(y,x) & \text{var}(y) \end{bmatrix}
\end{aligned}
\end{equation}
이 때, 조건부 pdf $p(y|x)$ 또한 가우시안 분포를 따른다. 자세한 유도 과정은 Appendix 10A를 참고하면 된다.
\begin{equation} \label{eq:bay7}
\boxed{ \begin{aligned}
& \mathbb{E}(y|x) = \mathbb{E}(y) + \frac{\text{cov}(x,y)}{\text{var}(x)}(x-\mathbb{E}(x)) \\
& \text{var}(y|x) = \text{var}(y) - \frac{\text{cov}^2(x,y)}{\text{var}(x)}
\end{aligned} }
\end{equation}
조건부 pdf는 다음과 같이 해석할 수 있다. $x$가 관찰되기 전까지 확률 변수 $y$는 $p(y) \sim \mathcal{N}(\mathbb{E}(y), \text{var}(y))$를 따르고 있다. $x$가 관찰되면 $y$는 평균과 분산이 (\ref{eq:bay7})처럼 약간 변한 가우시안 분포가 된다. 이 때, 두 확률 변수는 서로 종속적이라고 가정한다($\text{cov}(x,y)\neq0$). $y$에 대한 조건부 pdf는 점점 더 불확실성이 줄어들면서 뾰족한 모양이 된다.
$y$의 불확실성이 줄어든다는 것을 수학적으로 확인하기 위해 (\ref{eq:bay7}) 분산식을 다시 한 번 살펴보자.
\begin{equation}
\begin{aligned}
\text{var}(y|x) & = \text{var}(y)\bigg[ 1 - \frac{\text{cov}^2(x,y)}{\text{var}(x)\text{var}(y)} \bigg] \\
& = \text{var}(y)(1-\rho^2)
\end{aligned}
\end{equation}
- $\rho = \frac{\text{cov}^2(x,y)}{\text{var}(x)\text{var}(y)}$
$\rho$는 두 변수의 상관계수(cross-correlation coefficient)라고 하며 $|\rho|\ \leq 1$의 조건을 만족한다. 이전 섹션에서 $\mathbb{E}(y|x)$는 $y$에 대한 MMSE 추정값임을 배웠다. 따라서 (\ref{eq:bay7})의 평균은 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
\hat{y} = \mathbb{E}(y) + \frac{\text{cov}(x,y)}{\text{var}(x)}(x-\mathbb{E}(x))
\end{aligned}
\end{equation}
$\mathbb{E}(y)$를 이항하고 양변에 $\sqrt{\text{var}(y)}$를 나누어주고 $\text{var}(x)\rightarrow \sqrt{\text{var}(x)}\sqrt{\text{var}(x)}$로 나누어 주면 다음과 같은 정규화된 형태를 얻을 수 있다. 이 때 평균은 $0$이고 분산은 $1$을 가진다.
\begin{equation}
\begin{aligned}
& \frac{\hat{y} - \mathbb{E}(y)}{\sqrt{\text{var}(y)}} = \frac{\text{cov}(x,y)}{\sqrt{\text{var}(x)\text{var}(y)}}\frac{x-\mathbb{E}(x)}{\sqrt{\text{var}(x)}} \\
& \therefore \hat{y}_n = \rho x_n
\end{aligned}
\end{equation}
위 식에서 보다시피 $\rho$는 정규화된 관측값 $x_n$의 크기를 조절하여 정규화된 MMSE 추정값 $\hat{y}_n$의 값을 구하는데 사용된다. 만약 두 확률 변수가 이미 정규화된 경우 ($\mathbb{E}(x)= \mathbb{E}(y)=0, \text{var}(x)=\text{var}(y)=1$)면 분산 타원형 등고선(contour)는 아래 그림과 같이 얻어진다.

조건부 pdf의 피크(peak) 값은 $y=\rho x$ 직선 위에서 얻을 수 있다. 따라서 MMSE 추정값 $\mathbb{E}(y|x)$은 두 확률 변수의 상관 관계를 이용하여 추정값을 평가한다는 것을 알 수 있다. BMSE를 다시 쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}) & = \int \text{var}(y|x) p(\mathbf{x}) d\mathbf{x} \\
& = \text{var}(y|x) \\
& = \text{var}(y)(1-\rho^2)
\end{aligned}
\end{equation}
위 식에서 보다시피 posterior의 분산은 $x$와 독립적이기 때문에 추정값의 성능은 상관 계수 $\rho$에만 의존적인 것을 알 수 있다. 상관 관계는 이름처럼 결국 두 확률 변수 $x,y$의 통계적 상관성과 관련이 있으므로 추정값의 성능은 결국 두 확률 변수의 상관성과 관련이 있음을 알 수 있다.
지금까지 이변량 가우시안(bivariate Gaussian)에 대해 알아봤다면 이제는 이를 일반화시켜서 두 벡터 확률 변수 $[\mathbf{x}^{\intercal}, \ \mathbf{y}^{\intercal}]^{\intercal}$이 주어졌을 때 둘 사이의 다변량 가우시안 분포 함수(multivariate Gaussian pdf)에 대해 알아보자.
10.3.2. Theorem 10.2 (Conditional PDF of Multivariate Gaussian)
두 벡터 확률 변수 $\mathbf{x} \in \mathbb{R}^{k \times 1}$와 $\mathbf{y} \in \mathbb{R}^{l \times 1}$가 주어졌을 때 둘의 joint pdf는 다음과 같이 나타낼 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
p(\mathbf{x},\mathbf{y}) = \frac{1}{(2\pi)^{\frac{k+l}{2}} \det^{\frac{1}{2}}(\mathbf{C})} \exp\bigg[ -\frac{1}{2} \begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix}^{\intercal}\mathbf{C}^{-1} \begin{bmatrix} \mathbf{x} - \mathbb{E}(\mathbf{x}) \\ \mathbf{y} - \mathbb{E}(\mathbf{y}) \end{bmatrix} \bigg]
\end{aligned} }
\end{equation}
\begin{equation}
\begin{aligned}
& \text{where, } \mathbb{E}\bigg( \begin{bmatrix} \mathbf{x}\\ \mathbf{y} \end{bmatrix} \bigg) = \begin{bmatrix} \mathbb{E}(\mathbf{x}) \\ \mathbb{E}(\mathbf{y}) \end{bmatrix} \\
& \mathbf{C} = \begin{bmatrix} \mathbf{C}_{xx} & \mathbf{C}_{xy} \\ \mathbf{C}_{yx} & \mathbf{C}_{yy} \end{bmatrix} = \begin{bmatrix} k\times k & k\times l \\ l \times k & l\times l \end{bmatrix}
\end{aligned}
\end{equation}
이 때, 조건부 pdf $p(\mathbf{y}|\mathbf{x})$ 또한 가우시안 분포를 따른다. 자세한 유도 과정은 Appendix 10A를 참고하면 된다.
\begin{equation} \label{eq:bay11}
\boxed{ \begin{aligned}
& \mathbb{E}(\mathbf{y}|\mathbf{x}) = \mathbb{E}(\mathbf{y}) + \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}(\mathbf{x}-\mathbb{E}(\mathbf{x})) \\
& \mathbf{C}_{y|x} = \mathbf{C}_{yy} - \mathbf{C}_{yx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xy}
\end{aligned} }
\end{equation}
위 식에서 posterior의 공분산은 $\mathbf{x}$와 독립적임에 주목하자. 이러한 특성은 추후 섹션에서 유용하게 사용된다. 앞서 설명하였듯이 벡터 케이스에서도 $\mathbf{x}, \mathbf{y}$가 서로 결합 분포를 이루면(joint gaussian), $p(\mathbf{y})$와 $p(\mathbf{y}|\mathbf{x})$는 둘 다 가우시안 분포를 따른다.
10.4. Bayesian Linear Model
다음과 같은 데이터 모델이 주어졌다고 하자.
\begin{equation}
\begin{aligned}
x[n] = A + w[n] \quad n=0,1,\cdots,N-1
\end{aligned}
\end{equation}
- $w[n] \sim \mathcal{N}(0, \sigma^2)$ : WGN
그리고 베이지안 철학에 따라 $A \sim \mathcal{N}(\mu_A, \sigma_A^2)$라고 하자. 이를 벡터 형태로 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{x} = \mathbf{1}A + \mathbf{w}
\end{aligned}
\end{equation}
이는 파라미터 $A$가 확률 변수라는 것만 제외하면 앞선 챕터에서 말한 선형 모델과 동일하다. 위 식을 다음과 같이 일반적인 형태로 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{x} = \mathbf{H}\boldsymbol{\theta} + \mathbf{w}
\end{aligned}
\end{equation}
- $\mathbf{x} \in \mathbb{R}^{N\times 1}$
- $\mathbf{H} \in \mathbb{R}^{N\times p}$
- $\boldsymbol{\theta} \in \mathbb{R}^{p\times 1} \sim \mathcal{N}(\boldsymbol{\mu}_{\theta}, \mathbf{C}_{\theta})$
- $\mathbf{w} \in \mathbb{R}^{N\times 1} \sim \mathcal{N}(0, \mathbf{C}_{w})$ : $\boldsymbol{\theta}$와 독립적
위와 같은 선형 모델을 베이지안 일반 선형 모델(Bayesian general linear model)이라고 한다. 위 식에서 $p(\boldsymbol{\theta}|\mathbf{x})$의 값이 어떻게 나올지 궁금해할 수 있다. 이는 베이지안 추정 방법에 따라 두 확률 변수 $\mathbf{x}, \boldsymbol{\theta}$가 결합 분포를 이루므로(jointly gaussian) $p(\boldsymbol{\theta}|\mathbf{x})$ 또한 가우시안 분포를 가짐을 알 수 있다. $\mathbf{z} = [ \mathbf{x}^{\intercal}, \ \boldsymbol{\theta}^{\intercal}]^{\intercal}$과 같이 정의했을 때 이를 자세히 보면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{z} & = \begin{bmatrix} \mathbf{H}\boldsymbol{\theta} + \mathbf{w} \\ \boldsymbol{\theta} \end{bmatrix} \\
& = \begin{bmatrix} \mathbf{H} & \mathbf{I}_N \\ \mathbf{I}_p & \mathbf{0}_N \end{bmatrix} \begin{bmatrix} \boldsymbol{\theta} \\ \mathbf{w} \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathbf{I}_N \in \mathbb{R}^{N\times N}$
- $\mathbf{I}_p \in \mathbb{R}^{p\times p}$
- $\mathbf{0}_N \in \mathbb{R}^{N\times N}$
$\boldsymbol{\theta}$와 $\mathbf{w}$은 서로 독립이며 둘 중 하나는 가우시안 분포를 따르기 때문에 둘은 결합 분포를 이룸(jointly gaussian)을 알 수 있다. 추가적으로 $\mathbf{z}$는 두 확률 변수의 선형 변환이기 때문에 이 역시 가우시안 분포를 따름을 알 수 있다. 따라서 Theorem 10.2를 바로 적용할 수 있다. $\mathbf{x} = \mathbf{H}\boldsymbol{\theta} + \mathbf{w}$이고 $\mathbf{y}= \boldsymbol{\theta}$이 된다.
\begin{equation}
\begin{aligned}
& \mathbb{E}(\mathbf{x}) = \mathbb{E}(\mathbf{H}\boldsymbol{\theta} + \mathbf{w}) = \mathbf{H}\mathbb{E}(\boldsymbol{\theta}) = \mathbf{H} \boldsymbol{\mu}_{\theta} \\
& \mathbb{E}(\mathbf{y}) = \mathbb{E}(\boldsymbol{\theta}) = \boldsymbol{\mu}_{\theta} \\
\end{aligned}
\end{equation}
공분산 $\mathbf{C}_{xx}$은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{xx} & = \mathbb{E}[(\mathbf{x}-\mathbb{E}(\mathbf{x}))(\mathbf{x}-\mathbb{E}(\mathbf{x}))^{\intercal}] \\
& = \mathbb{E}[(\mathbf{H}\boldsymbol{\theta} + \mathbf{w} -\mathbf{H} \boldsymbol{\mu}_{\theta})(\mathbf{H}\boldsymbol{\theta} + \mathbf{w} -\mathbf{H} \boldsymbol{\mu}_{\theta})^{\intercal}] \\
& = \mathbb{E}[(\mathbf{H}(\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta}) + \mathbf{w})(\mathbf{H}(\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta}) + \mathbf{w})^{\intercal}] \\
& = \mathbf{H}\mathbb{E}[(\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta})(\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta})^{\intercal}]\mathbf{H}^{\intercal} + \mathbb{E}[\mathbf{w}\mathbf{w}^{\intercal}] \\
& = \mathbf{H}\mathbf{C}_{\theta}\mathbf{H}^{\intercal} + \mathbf{C}_{w} \\
\end{aligned}
\end{equation}
$\boldsymbol{\theta}$와 $\mathbf{w}$가 서로 독립적이라는 사실에 유의하여 $\mathbf{C}_{yx}$를 구해보면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{yx} & = \mathbb{E}[(\mathbf{y}-\mathbb{E}(\mathbf{y}))(\mathbf{x}-\mathbb{E}(\mathbf{x}))^{\intercal}] \\
& = \mathbb{E}[ (\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta})( \mathbf{H} (\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta}) + {\color{Mahogany} \cancel{\mathbf{w}} } )^{\intercal} ] \\
& = \mathbb{E}[ (\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta})( \mathbf{H} (\boldsymbol{\theta}-\boldsymbol{\mu}_{\theta}))^{\intercal} ] \\
& = \mathbf{C}_{\theta}\mathbf{H}^{\intercal}
\end{aligned}
\end{equation}
10.4.1. Theorem 10.3 (Posterior PDF for the Bayesian General Linear Model)
관측 데이터 $\mathbf{x}$가 다음과 같은 선형 모델로 표현될 수 있는 경우
\begin{equation}
\begin{aligned}
\mathbf{x} = \mathbf{H}\boldsymbol{\theta} + \mathbf{w}
\end{aligned}
\end{equation}
- $\mathbf{x} \in \mathbb{R}^{N\times 1}$
- $\mathbf{H} \in \mathbb{R}^{N\times p}$
- $\boldsymbol{\theta} \in \mathbb{R}^{p\times 1} \sim \mathcal{N}(\boldsymbol{\mu}_{\theta}, \mathbf{C}_{\theta})$
- $\mathbf{w} \in \mathbb{R}^{N\times 1} \sim \mathcal{N}(0, \mathbf{C}_{w})$ : $\boldsymbol{\theta}$와 독립적
Posterior pdf $p(\boldsymbol{\theta}|\mathbf{x})$의 평균과 공분산은 다음과 같이 나타낼 수 있다.
\begin{equation} \label{eq:bay8}
\boxed{ \begin{aligned}
& \mathbb{E}(\boldsymbol{\theta}|\mathbf{x}) = \boldsymbol{\mu}_{\theta} + \mathbf{C}_{\theta}\mathbf{H}^{\intercal}(\mathbf{H}\mathbf{C}_{\theta}\mathbf{H}^{\intercal} + \mathbf{C}_{w})^{-1} (\mathbf{x} - \mathbf{H}\boldsymbol{\mu}_{\theta}) \\
& \mathbf{C}_{\theta|x} = \mathbf{C}_{\theta} - \mathbf{C}_{\theta}\mathbf{H}^{\intercal}(\mathbf{H}\mathbf{C}_{\theta}\mathbf{H}^{\intercal} + \mathbf{C}_{w})^{-1}\mathbf{H}\mathbf{C}_{\theta}
\end{aligned} }
\end{equation}
고전적인 추정 문제의 선형 모델과 비교해보면 $(\mathbf{H}\mathbf{C}_{\theta}\mathbf{H}^{\intercal} + \mathbf{C}_{w})$의 역행렬을 구하기 위해 $\mathbf{H}$ 행렬은 반드시 full rank가 아니어도 된다. 추후 섹션에서 설명의 편의를 위해 (\ref{eq:bay8})의 변형된 버전에 대하여 설명한다.
\begin{equation}
\boxed{ \begin{aligned}
& \mathbb{E}(\boldsymbol{\theta}|\mathbf{x}) = \boldsymbol{\mu}_{\theta} + (\mathbf{C}_{\theta}^{-1} + \mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1}\mathbf{H})^{-1} \mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1} (\mathbf{x} - \mathbf{H}\boldsymbol{\mu}_{\theta}) \\
& \mathbf{C}_{\theta|x} = (\mathbf{C}_{\theta}^{-1} + \mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1}\mathbf{H})^{-1} \\
& \mathbf{C}_{\theta|x}^{-1} = \mathbf{C}_{\theta}^{-1} + \mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1}\mathbf{H}
\end{aligned} }
\end{equation}
위 식에서 보다시피 만약 사전 지식(prior knowledge)가 주어지지 않는다면($\boldsymbol{\mu}_{\theta} \rightarrow 0, \mathbf{C}_{\theta}^{-1} \rightarrow 0$) , MMSE 추정값은 $\hat{\boldsymbol{\theta} } = \mathbb{E}( \boldsymbol{\theta} |\mathbf{x})= (\mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1}\mathbf{H})^{-1} \mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1} \mathbf{x}$가 되어서 선형 모델의 MVUE와 동일한 공식을 얻는다.
10.5. Bayesian Estimation for Deterministic Parameters
베이지안 추정 방법은 엄밀히 말해서 파라미터 $\theta$ 랜덤한 확률 변수일 때만 적용되지만, 실제로는 결정론적(deterministic) 파라미터 추정에도 종종 사용된다. 이는 베이지안 가정을 사용하여 추정값을 도출하고 마치 $\theta$가 랜덤 변수가 아닌 것처럼 그 추정값을 사용하는 것을 의미한다. 이러한 상황은 MVUE가 존재하지 않을 때 발생할 수 있다. 예를 들어, 우리가 분산 측면에서 다른 추정기들보다 일관되게 우수한 불편추정값(unbiased estimator)을 찾지 못할 수도 있지만 베이지안 프레임워크 내에서 MMSE는 항상 존재하고 이는 다양한 $\theta$ 값들에 대해 평균적으로 잘 작동하는 추정값을 제공한다. 하지만 평균적으로 잘 작동한다는 것일뿐 가끔씩 안 좋은 성능을 낼 수도 있음을 유의하자.
Example 10.1 문제를 다시 보자. (\ref{eq:bay9}) 식을 보면 다음과 같다.
\begin{equation} \label{eq:bay10}
\begin{aligned}
\hat{A} & = \frac{\sigma_A^2}{\sigma^2_A + \frac{\sigma^2}{N}}\bar{x} + \frac{\frac{\sigma^2}{N}}{\sigma^2_A + \frac{\sigma^2}{N}}\mu_A \\
& = \alpha \bar{x} + (1-\alpha) \mu_A
\end{aligned}
\end{equation}
- $\alpha = \frac{\sigma_A^2}{\sigma^2_A + \frac{\sigma^2}{N}}$
$\alpha$는 $0 \leq \alpha \leq 1$의 값을 가지는 가중치 값이다. 만약 $A$가 결정론적(deterministic) 파라미터이라고 가정해보자. MSE에 위 식을 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{mse}(\hat{A}) & = \text{var}(\hat{A}) + b^2(\hat{A}) \\
& = \alpha^2 \text{var}(\bar{x}) + [ \alpha A + (1-\alpha)\mu_A - A ]^2 \\
& = {\color{Red} \alpha^2\frac{\sigma^2}{N} } + {\color{Cyan} (1-\alpha)^2(A - \mu_A)^2 }
\end{aligned}
\end{equation}
- $b(\hat{A}) = \mathbb{E}(\hat{A}) - A$ : 편향(bias)
위 식에서 보다시피 베이지안 추정값을 사용하면 $0 \leq \alpha^2 \leq 1$에 의해 분산을 줄일 수 있지만(빨강), 편향(bias) 성분이 상당히 증가하는 것을 볼 수 있다(파랑).

위 그림에서 보다시피 베이지안 추정값은 파라미터 $A$가 prior mean $\mu_A$ 근처에 있을 때만 MVUE $\bar{x}$보다 낮은 MSE 값을 가진다. 그렇지 않으면 오히려 성능이 떨어진다. 이렇듯 베이지안 추정 문제에서는 다른 모든 추정값들보다 MSE가 낮은 하나의 추정값은 존재하지 않지만 '평균적으로' 좋은 추정값은 존재한다. BMSE를 구해보면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}) & = \mathbb{E}_A[\text{mse}(\hat{A})] \\
& = \alpha^2 \frac{\sigma^2}{N} + (1-\alpha)^2 \mathbb{E}_A[(A-\mu_A)^2] \\
& = \alpha^2 \frac{\sigma^2}{N} + (1-\alpha)^2 \sigma^2_A \\
& = \frac{\sigma^2}{N} \frac{\sigma^2_A}{\sigma^2_A +\frac{\sigma^2}{N}} \\
& < \frac{\sigma^2}{N} = \text{Bmse}(\bar{x})
\end{aligned}
\end{equation}
따라서 MSE는 조건적으로 베이지안 추정값 $\hat{A}$이 MVUE $\bar{x}$보다 높을 수 있지만 BMSE는 $\hat{A}$이 항상 작은 것을 알 수 있다. 결국 베이지안 추정 방법을 통해 파라미터 $A$의 사전 지식을 안다는 것은 평균적으로 좋은 성능을 발휘하지만 가끔씩 안 좋은 prior를 추정하게 되면 MVUE보다 성능이 낮을 수 있음을 의미한다.
11. General Bayesian Estimators
이전 챕터에서는 베이지안 추정 방법을 사용하여 파라미터를 추정하는 방법에 대해 배웠다. 이번 챕터에서는 일반적인 베이지안 추정값들과 그들의 성질에 대해 배운다. 이를 위해 Bayes risk에 대해 설명한다. 그리고 Bayes risk를 최소화함으로써 다양한 추정값들을 얻는 내용에 대해 배운다. 주목할만한 추정값은 MMSE 추정값과 maxmimum a posteriori 추정값이다. 마지막으로 베이지안 추정값의 성능에 대해 평가한다.
11.1. Risk Functions
이전 챕터에서 우리는 $\mathbb{E}[(\theta-\hat{\theta})^2]$의 값을 최소화하는 MMSE 추정값에 대해 배웠다. 에러를 $\epsilon= \theta-\hat{\theta}$라고 정의하자. $\epsilon$은 $\mathbf{x}$와 $\theta$에 대한 추정값의 에러를 의미한다. 그리고 비용 함수(cost function)를 $\mathcal{C}( \epsilon)$로 정의하자. 비용 함수의 기대값은 Bayes risk $\mathcal{R}$이라고 정의하자. Bayes risk $\mathcal{R}$은 주어진 추정값의 성능을 평가해주는 criterion 함수이다. 지금까지 정의한 내용을 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathcal{R}=\mathbb{E}[\mathcal{C}(\epsilon)]
\end{aligned}
\end{equation}

위 그림과 같이 세 가지 서로 다른 비용 함수를 알아보자. Quadratic 비용함수는 에러의 제곱을 적용한 형태이다.
\begin{equation}
\begin{aligned}
\mathcal{C}( \epsilon)= \epsilon^2 \quad \cdots \text{ quadratic error}
\end{aligned}
\end{equation}
비용 함수가 위와 같은 경우 Bayes risk $\mathcal{R}$는 MSE가 된다. 비용 함수는 2차식 이외에도 다양한 형태가 될 수 있다. 다음으로 absolute 비용함수에 대해 알아보면 다음과 같다. 이는 에러에 절대값을 적용한 형태이다.
\begin{equation}
\begin{aligned}
\mathcal{C}(\epsilon) = |\epsilon| \quad \cdots \text{ absolute error}
\end{aligned}
\end{equation}
마지막 비용 함수는 hit-or-miss 비용 함수라고 불리며 $\delta$ 보다 작은 에러 값은 반영을 하지 않고 $\delta$보다 큰 값들은 항상 $1$로만 반영하는 비용 함수이다.
\begin{equation}
\begin{aligned}
\mathcal{C}(\epsilon)=\begin{cases} 0 \quad & |\epsilon| < \delta \\1 \quad & |\epsilon| > \delta\end{cases} \quad \cdots \text{ hit-or-miss error}
\end{aligned}
\end{equation}
$\delta$는 항상 $0$보다 크다. 방금 소개한 세 가지 비용 함수는 양의 에러 또는 음의 에러를 구분하지 않고 전부 동일하게 처리하는 공통점이 있다. 물론 이러한 가정은 실제 추정 문제에서는 대부분 참이 아니다.
Bayes risk $\mathcal{R}$에 대한 최적의 추정값을 얻기 위해 이를 자세히 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathcal{R} & = \mathbb{E}(\mathcal{C}(\epsilon)] \\
& = \int\int \mathcal{C}(\theta-\hat{\theta}) p(\mathbf{x},\theta) d\mathbf{x}d\theta \\
& = \int \bigg[ \int \mathcal{C}(\theta-\hat{\theta}) p(\theta|\mathbf{x}) d\theta \bigg] p(\mathbf{x}) d\mathbf{x} \\
\end{aligned}
\end{equation}
챕터 10에서 다룬 내용과 동일하게 위 브라켓 안에 있는 값만 최소화하면 된다. 브라켓 안의 $\mathbf{x}$ 값은 주어진 상수가 되고 $\hat{\theta}$ 값은 스칼라 변수가 된다.
Quadratic error case:
$\mathcal{C}(\epsilon)=\epsilon^2$인 경우 MMSE 추정값을 얻는다는 사실을 이전 챕터에서 이미 설명하였기 때문에 자세한 설명은 생략한다. MMSE 추정값 $\hat{\theta} = \mathbb{E}(\theta|\mathbf{x})$는 posterior pdf의 평균(mean)을 의미한다.
Absolute error case:
다음으로 $\mathcal{C}(\epsilon)=|\epsilon|$ 케이스를 보자. 이를 위 브라켓 안에 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
g(\hat{\theta}) & = \int |\theta-\hat{\theta}| p(\theta|\mathbf{x}) d\theta \\
& = \int_{-\infty}^{\hat{\theta}} (\theta-\hat{\theta})p(\theta|\mathbf{x}) d\theta + \int^{\infty}_{\hat{\theta}} (\theta-\hat{\theta})p(\theta|\mathbf{x}) d\theta
\end{aligned}
\end{equation}
위 식은 라이프니츠 정리(Leibnitz rule)에 의해 다음과 같이 정리된다.
\begin{equation}
\begin{aligned}
\frac{\partial g(\hat{\theta})}{\partial \hat{\theta}} = \int_{-\infty}^{\hat{\theta}} p(\theta|\mathbf{x}) d\theta - \int^{\infty}_{\hat{\theta}} p(\theta|\mathbf{x}) d\theta =0
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
\therefore \int_{-\infty}^{\hat{\theta}} p(\theta|\mathbf{x}) d\theta = \int^{\infty}_{\hat{\theta}} p(\theta|\mathbf{x}) d\theta \quad \cdots \text{Median of PDF}
\end{aligned} }
\end{equation}
위 식에서 보다시피 $\hat{\theta}$를 기점으로 $-\infty, \infty$까지 적분한 확률 크기가 같으려면 $\hat{\theta}$는 중앙값에 위치해야만 한다. 따라서 absolute 비용 함수를 사용했을 때 Bayes risk를 최소화하는 값은 posterior pdf의 중앙값(median)이 된다.
Hit-or-miss case:
다음으로 비용 함수가 hit-or-miss인 경우$\bigg( \mathcal{C}(\epsilon)=\begin{cases} 0 \quad & |\epsilon| < \delta \\1 \quad & |\epsilon| > \delta\end{cases} \bigg)$에 대해 알아보자.
\begin{equation}
\begin{aligned}
g(\hat{\theta}) & = \int_{-\infty}^{\hat{\theta}-\delta} 1\cdot p(\theta|\mathbf{x}) d\theta + \int^{\infty}_{\hat{\theta}+\delta} 1\cdot p(\theta|\mathbf{x}) d\theta
\end{aligned}
\end{equation}
확률의 정의에 의해 $\int_{-\infty}^{\infty} p(\theta|\mathbf{x}) d\theta =1$를 만족해야 하므로 위 식은 다음과 같이 정리된다.
\begin{equation}
\begin{aligned}
g(\hat{\theta}) & = 1 - \int_{\hat{\theta}-\delta}^{\hat{\theta}+\delta} p(\theta|\mathbf{x}) d\theta
\end{aligned}
\end{equation}
위 식은 $\int_{\hat{\theta}-\delta}^{\hat{\theta}+\delta} p(\theta|\mathbf{x}) d\theta$를 최대화시킴으로써 Bayes risk를 최소화시킬 수 있다. 충분히 작은 $\delta$에 대하여 $\hat{\theta}$를 찾는 문제는 가장 큰 $p(\theta|\mathbf{x})$ 값을 찾는 문제와 동치이다. 따라서 hit-or-miss 비용 함수를 사용했을 때 Bayes risk를 최소화하는 값은 posterior pdf의 최빈값(mode)가 된다. 이는 maximum a posteriori(MAP) 추정값이라고도 부른다.
정리하면 Bayes risk를 최소화하는 추정값은 비용 함수에 따라 다르며 quadratic, absolute, hit-or-miss 비용 함수에 대하여 각각 posterior pdf의 mean, median, mode를 의미한다. 만약 pdf가 가우시안 분포를 따른다면 mean, median, mode는 전부 동일한 값을 가진다.
\begin{equation}
\begin{aligned}
p(\theta|\mathbf{x}) = \frac{1}{ \sqrt{ 2\pi\sigma_{\theta|x}^{2} }} \exp\bigg[ -\frac{1}{2\sigma_{\theta|x}^{2}} (\theta - \mu_{\theta|x})^{2} \bigg]
\end{aligned}
\end{equation}

11.2. Maximum A Posteriori Estimators
MAP 추정값은 다음과 같이 posterior pdf의 값을 최대화하는 $\hat{\theta}$로 정의된다.
\begin{equation}
\begin{aligned}
\hat{\theta} = \arg\max_{\theta} \ p(\theta|\mathbf{x})
\end{aligned}
\end{equation}
이는 이전 섹션에서 Bayes risk의 비용 함수가 hit-or-miss인 경우 최적의 추정값이 MAP임을 배웠다. Posterior pdf를 베이즈 규칙에 따라 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
p(\theta|\mathbf{x}) = \frac{p(\mathbf{x}|\theta)p(\theta)}{p(\mathbf{x})}
\end{aligned}
\end{equation}
위 식에서 보다시피 MAP은 $p(\mathbf{x}|\theta)p(\theta)$를 최대화 하는 것과 동일하다. 이는 MLE 추정값에 prior 정보가 결합된 형태로 해석할 수 있다. 따라서 MAP 추정값은 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{\theta} = \arg\max_{\theta} \ p(\mathbf{x}|\theta)p(\theta)
\end{aligned}
\end{equation}
위 식 우항에 log를 취해도 결과는 변하지 않으므로 다음 식이 성립한다.
\begin{equation} \label{eq:map1}
\begin{aligned}
\hat{\theta} = \arg\max_{\theta} \ \ln p(\mathbf{x}|\theta) + \ln p(\theta)
\end{aligned}
\end{equation}
벡터 파라미터로 MAP 추정값을 확장하기 전에 우선 스칼라 케이스에 대해 알아보자.
11.2.1. Example 11.2 - Exponential PDF
다음과 같은 exponential 확률 분포가 주어졌다고 하자.
\begin{equation}
\begin{aligned}
p(x[n]|\theta) = \begin{cases}
\theta \exp(-\theta x[n]) \quad & x[n]>0 \\
0 \quad & x[n]<0
\end{cases}
\end{aligned}
\end{equation}
- $x[n]$: i.i.d
모든 데이터에 대한 확률 분포는 다음과 같다.
\begin{equation}
\begin{aligned}
p(\mathbf{x}|\theta) = \Pi_{n=0}^{N-1} p(x[n]| \theta)
\end{aligned}
\end{equation}
Prior pdf도 exponential 확률 분포를 따른다고 가정하자.
\begin{equation}
\begin{aligned}
p(\theta) = \begin{cases}
\lambda \exp(-\lambda \theta) \quad & \theta>0 \\
0 \quad & \theta<0
\end{cases}
\end{aligned}
\end{equation}
(\ref{eq:map1})에 위 식을 대입해보면 다음과 같다.
\begin{equation}
\begin{aligned}
g(\theta) & = \ln p(\mathbf{x}|\theta) + \ln p(\theta) \\
& = \ln\bigg[ \theta^{N} \exp\bigg( -\theta\sum_{n=0}^{N-1}x[n] \bigg) \bigg] + \ln[\lambda\exp(-\lambda \theta)] \\
& = N\ln \theta - N\theta\bar{x} + \ln\lambda -\lambda\theta
\end{aligned}
\end{equation}
이 때, $\theta>0$이라고 가정한다. 위 식을 미분 후 $0$으로 놓고 풀면 exponential pdf에 대한 MAP 추정값을 얻을 수 있다.
\begin{equation}
\begin{aligned}
\frac{\partial g(\theta)}{\partial \theta} = \frac{N}{\theta} - N\bar{x} - \lambda = 0
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
\hat{\theta} = \frac{1}{\bar{x} + \frac{\lambda}{N}}
\end{aligned} }
\end{equation}
만약 데이터가 충분히 많다면 ($N \rightarrow \infty$), $\hat{\theta} \rightarrow \frac{1}{\bar{x}}$인 것을 알 수 있다. 또한 사전 지식이 균일 분포에 가까운 모양될수록($\lambda \rightarrow 0$), 역시 $\hat{\theta} \rightarrow \frac{1}{\bar{x}}$인 것을 알 수 있다. 이는 베이지안 MLE를 수행한 것과 동일하다. $\lambda$가 $0$에 가까워질수록 likelihood $p(\mathbf{x}|\theta)$ 값이 prior pdf $p(\theta)$보다 커지게 되고 따라서 prior pdf의 영향은 점점 작아진다.
11.2.2. Scalar MAP estimator v.s. vector MAP estimator
이번 섹션에서는 MAP 추정값을 벡터 파라미터로 확장해보자. 우선 스칼라 MAP 추정값은 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{\theta} = \arg\max_{\theta} \ p(\theta|\mathbf{x})
\end{aligned}
\end{equation}
스칼라 MAP 추정값의 장점은 오직 하나의 파라미터에 대한 $p(\mathbf{x}|\theta)p(\theta)$만 구하면 된다는 것이다. 따라서 여러 파라미터를 결합하는 과정이 생략된다. 벡터 MAP 추정값은 다음과 같이 정의할 수 있다.
\begin{equation}
\begin{aligned}
\hat{\boldsymbol{\theta}} = \arg\max_{\boldsymbol{\theta}} \ p(\boldsymbol{\theta}|\mathbf{x})
\end{aligned}
\end{equation}
벡터 MAP 추정값은 스칼라 버전과는 다른 값이 계산될 수 있다. 스칼라 MAP 추정값은 주어진 데이터 $x$에 대해 하나의 파라미터 $\theta$의 사후 확률을 최대화하는 값을 찾는다. 반면에, 벡터 MAP 추정값은 여러 파라미터 $\theta_1, \theta_2, \cdots, \theta_{i}$의 결합 사후 확률을 최대화하는 값을 찾는다. 결합 분포(joint pdf)를 고려할 때는 두 변수 간의 관계가 중요해지며 이는 벡터 MAP 추정값이 더 복잡한 상황을 반영한 최적값을 계산한다고 볼 수 있다.

예를 들어 $p(\theta_1, \theta_2|\mathbf{x})$가 위 왼쪽 그림과 같은 결합 분포를 가진다고 하자. $\theta_2$에 대한 벡터 MAP 추정값은 직관적으로 결합 분포에서 확률이 1/3로 제일 높은 $0 < \hat{\theta}_{2} < 1$ 구간 안에 존재할 것이다. 하지만 이를 오직 스칼라 $\hat{\theta}_{2}$에 대해서만 추정하게 되면 상황이 달라진다. $p(\theta_1, \theta_2|\mathbf{x})$를 $\theta_2$에 대하여 주변화(marginalize)해보자.
\begin{equation}
\begin{aligned}
p(\theta_2|\mathbf{x}) & = \int p(\theta_1, \theta_2|\mathbf{x}) d\theta_1 \\
& = \begin{cases}
\int_2^3 \frac{1}{3} d \theta_1 \quad & 0<\theta_2<1 \\
\int_0^2 \frac{1}{6} d \theta_1 + \int_3^5 \frac{1}{6} d\theta_1 \quad & 1<\theta_1<2
\end{cases} \\
& = \begin{cases}
\frac{1}{3} \quad & 0<\theta_2 < 1\\
\frac{2}{3} \quad & 1<\theta_2 < 2
\end{cases}
\end{aligned}
\end{equation}
위 그림 오른쪽에서 보는 것과 같이 동일한 구간에 대한 확률이 달라졌다. 따라서 $p(\theta_2|\mathbf{x})$에 대한 MAP 추정값은 확률이 제일 높은 $1 < \hat{\theta}_{2} < 2$ 구간 간에 존재하게 된다. 이는 두 파라미터가 결합 분포를 이뤘을 때(jointly gaussian)와 다른 MAP 추정값이다. 따라서 벡터 MAP 추정값은 Bayes risk를 최소화하는 것은 맞지만 더 이상 hit-or-miss 비용 함수를 최소화하는 것은 아니다.
11.2.3. Example 11.5 - Exponential PDF
Example 11.2 예제에서 기존 파라미터 $\theta$의 비선형 변환된 파라미터 $\alpha=1/\theta$를 추정하는 문제에 대해 생각해보자. MAP 추정값 $\hat{\alpha}$은 다음과 같이 가정할 수 있다.
\begin{equation}
\begin{aligned}
\hat{\alpha} = \frac{1}{\hat{\theta}}
\end{aligned}
\end{equation}
$\hat{\theta}$는 $\theta$에 대한 MAP 추정값을 의미하며 이전 예제에서 $\hat{\theta} = \frac{1}{\bar{x} + \frac{\lambda}{N}}$임을 알고 있다. 그렇다면 $\hat{\alpha}$는 다음과 같을까?
\begin{equation} \label{eq:map2}
\begin{aligned}
\hat{\alpha} = \bar{x} + \frac{\lambda}{N}
\end{aligned}
\end{equation}
우리는 위 값이 틀렸다는 것을 증명할 것이다. Exponential 확률 분포로 돌아가서 $\alpha$를 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
p(x[n]|\theta) = \begin{cases}
\theta \exp(-\theta x[n]) \quad & x[n]>0 \\
0 \quad & x[n]<0
\end{cases}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\Rightarrow p(x[n]|\alpha) = \begin{cases}
\frac{1}{\alpha} \exp\big( -\frac{x[n]}{\alpha} \big) \quad & x[n]>0 \\
0 \quad & x[n]<0
\end{cases}
\end{aligned}
\end{equation}
위 식은 $\theta$에 대한 확률 분포가 아니기 때문에 바로 $\alpha$로 변환이 가능하다. 다음으로 prior pdf는 아래와 같다.
\begin{equation}
\begin{aligned}
p(\theta) = \begin{cases}
\lambda \exp(-\lambda \theta) \quad & \theta>0 \\
0 \quad & \theta<0
\end{cases}
\end{aligned}
\end{equation}
하지만 파라미터 $\theta$는 결정론적(deterministic) 파라미터가 아닌 확률 변수로 보기 때문에 위 식에 $\theta=1/\alpha$와 같이 바로 대입할 수 없다. 확률의 정의를 만족시키기 위해 분모에 $\alpha$에 대한 미분 값을 넣어줌으로써 크기를 $1$로 정규화시킨다.
\begin{equation}
\begin{aligned}
p_{\alpha}(\alpha) & = \frac{p_{\theta}(\theta(\alpha))}{\big| \frac{d \alpha}{d \theta} \big|} \\
& = \begin{cases}
\frac{\lambda \exp(-\lambda/\alpha )}{\alpha^2} \quad & \alpha >0 \\
0 \quad & \alpha<0
\end{cases}
\end{aligned}
\end{equation}
지금까지 유도한 식을 바탕으로 MAP 추정값을 찾아보자.
\begin{equation}
\begin{aligned}
g(\alpha) & = \ln p(\mathbf{x}|\alpha) + \ln p(\alpha) \\
& = \ln\bigg[ \big(\frac{1}{\alpha}\big)^{N} \exp\bigg( -\frac{1}{\alpha}\sum_{n=0}^{N-1}x[n] \bigg) \bigg] + \ln \frac{\lambda\exp(-\lambda /\alpha)}{\alpha^2} \\
& = -N\ln \alpha - N\frac{\bar{x}}{\alpha} + \ln\lambda -\frac{\lambda}{\alpha} - 2 \ln \alpha \\
& = -(N+2) \ln \alpha - \frac{N\bar{x} + \lambda}{\alpha} + \ln\lambda
\end{aligned}
\end{equation}
위 식을 $\alpha$에 대하여 미분 후 0으로 놓으면 다음과 같은 MAP 추정값이 구해진다.
\begin{equation}
\begin{aligned}
\frac{d g}{d \alpha} = -\frac{N+2}{\alpha} + \frac{N\bar{x}+\lambda}{\alpha^2} = 0
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
\hat{\alpha} = \frac{N\bar{x}+\lambda}{N+2}
\end{aligned} }
\end{equation}
이는 앞서 예상한 (\ref{eq:map2})와 다르다는 것을 알 수 있다. 이를 통해 MAP 추정값은 비선형 변환에 대하여 교환 법칙이 성립하지 않는다는 것을 알 수 있다. 이는 MLE의 Invariance 성질과 대조되는 부분이다.
11.3. Performance Description
고전적인 추정 문제에서 우리는 추정값의 평균과 분산에 관심을 두었다. 만약 추정값이 가우시안 분포를 따른다고 하면 우리는 이를 통해 바로 pdf를 구할 수 있었다. 만약 pdf가 참값(true value) 주변에 집중되어 있다면 우리는 그 추정값의 성능이 좋다고 말할 수 있었다.
하지만 베이지안 추정 문제에서 파라미터는 확률 변수(random variable)로 취급되므로 이와 같은 접근법을 사용할 수 없다. 파라미터의 랜덤성으로 인해 각 $\theta$가 샘플링될 때마다 다른 pdf가 생성된다. 이러한 pdf를 $p(\hat{\theta}| \theta)$라고 표기하자. 좋은 추정값의 성능을 위해 $\theta$와 $\hat{\theta}$의 차이는 거의 없어야 하며 이를 평가하기 위해 에러 $\epsilon$을 다음과 같이 정의한다.
\begin{equation}
\begin{aligned}
\epsilon = \theta - \hat{\theta}
\end{aligned}
\end{equation}
좋은 추정값을 얻기 위한 기준은 다음과 같다.
- 모든 가능한 추정값 $\hat{\theta}$은 $\theta$와 근접할 수록 좋다. 다시 말하면 에러 $\epsilon = \theta - \hat{\theta}$가 작아야 한다.
- 좋은 추정값 $\hat{\theta}$을 얻기 위해 $p(\hat{\theta}| \theta)$가 $\theta$ 주변에 집중적으로 분포해야 한다.
- 이를 만족하는 추정값은 $\mathbb{E}_{x,\theta}[( \theta - \hat{\theta})^2]$를 최소화하는 MMSE 추정값이된다.
베이지안 추정값의 성능을 평가할 때 항상 prior 분포 선정이 문제되므로 에러에 대한 pdf $p(\hat{\theta}| \theta)$를 평가하는 것은 적합한 절차이다. 좋은 추정값일 수록 $p(\hat{\theta}| \theta)$ 값이 $0$ 주변에 집중되어 있고 이는 곧 에러가 적다는 의미이다.
위 3번에서 MMSE 추정값은 $\hat{\theta} = \mathbb{E}(\theta|\mathbf{x})$이므로 이를 에러에 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
\epsilon = \theta - \mathbb{E}(\theta|\mathbf{x})
\end{aligned}
\end{equation}
에러의 평균은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbb{E}_{x,\theta}(\epsilon) & =\mathbb{E}_{x,\theta}[\theta - \mathbb{E}(\theta|\mathbf{x})] \\
& = \mathbb{E}_{x}[\mathbb{E}_{\theta|x}(\theta) - \mathbb{E}_{\theta|x}(\theta|\mathbf{x})] \\
& = \mathbb{E}_{x}[\mathbb{E}(\theta|\mathbf{x}) - \mathbb{E}(\theta|\mathbf{x})] \\
& = 0
\end{aligned}
\end{equation}
따라서 에러 pdf의 MMSE 추정값은 $0$이 된다. 분산은 다음과 같다.
\begin{equation}
\begin{aligned}
\text{var}(\epsilon) & = \mathbb{E}_{x,\theta}(\epsilon^2) \\
& = \mathbb{E}_{x,\theta}[( \theta - \hat{\theta})^2]
\end{aligned}
\end{equation}
분산은 BMSE의 최소값과 동일하다. 만약 $\epsilon$가 가우시안 분포를 따르는 경우 이는 다음과 같이 쓸 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\epsilon \sim \mathcal{N}(0, \text{Bmse}(\hat{\theta}))
\end{aligned} }
\end{equation}
11.3.1. Example 11.6 - DC Level in WGN - Gaussian Prior PDF
Example 10.1 문제를 다시 생각해보자. 우리는 (\ref{eq:bay9}) 추정값을 얻었었다.
\begin{equation}
\begin{aligned}
\hat{A} & = \frac{\sigma_A^2}{\sigma^2_A + \frac{\sigma^2}{N}}\bar{x} + \frac{\frac{\sigma^2}{N}}{\sigma^2_A + \frac{\sigma^2}{N}}\mu_A \\
\end{aligned}
\end{equation}
그리고 분산은 아래와 같았다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}) & = \frac{1}{\frac{N}{\sigma^2} + \frac{1}{\sigma_A}} \\
\end{aligned}
\end{equation}
에러를 $\epsilon=A-\hat{A}$라고 하자. $\hat{A}$는 데이터 $\mathbf{x}$에 선형 관계를 가지므로 $\mathbf{x}$와 $A$는 결합 분포를 이루고(jointly gaussian) 따라서 에러 또한 가우시안 분포를 따른다.
\begin{equation}
\begin{aligned}
\epsilon \sim \mathcal{N}\bigg( 0, \frac{1}{\frac{N}{\sigma^2} + \frac{1}{\sigma_A}} \bigg)
\end{aligned}
\end{equation}
위 식에서 보다시피 $N\rightarrow \infty$ 일수록 에러 pdf는 $0$에 수렴한다. 충분한 데이터가 관측된 경우 베이지안 추정값은 일관된(consistent) 추정값을 가진다고 하며 $\hat{A}$가 충분히 $A$에 가까워 졌음을 의미한다.
12. Linear Bayesian Estimators
이전 챕터에서 다뤘던 최적의 베이지안 추정값은 closed form으로 값을 결정하기 어려우며 실제로 구현하기에 계산적으로 매우 복잡하였다. 확률 변수들이 결합 분포를 이룬다는 가정 하에 추정값들은 비교적 쉽게 찾을 수 있었지만 이러한 가정은 실제 추정 문제에서는 참이 아닌 경우가 많다. 이번 챕터에서는 이러한 격차를 메우기 위해 MMSE criterion을 유지하면서도 추정값을 선형으로 제한하는 방법에 대해 소개한다. 그렇게 되면 BLUE에서도 설명하였듯이 추정값은 pdf의 첫 두 모멘트에만 의존하며 closed form 형태로 결정될 수 있다. 여러 방면에서 이 접근법은 고전적인 추정 방법과 유사하다. 실제 추정 문제에서 이러한 추정값들은 위너 필터(Wiener filters)라고 불리며 광범위하게 사용되고 있다.
12.1. Linear MMSE Estimation
스칼라 파라미터 $\theta$를 추정하기 위해 $N$개의 데이터 $\mathbf{x}=[x[0],x[1],\cdots,x[N-1]]^{\intercal}$이 관측되었다고 하자. 그리고 베이지안 철학에 의해 $\theta$ 또한 확률 변수라고 가정하자. $\theta$ 값은 $\mathbf{x}$의 선형 결합(사실 상 affine 결합)으로 다음과 같이 표현할 수 있다.
\begin{equation} \label{eq:lmmse1}
\begin{aligned}
\hat{\theta} = \sum_{n=0}^{N-1}a_n x[n] + a_N
\end{aligned}
\end{equation}
가중치 계수 $a_n$을 찾기 위해 BMSE를 최소화해야 한다.
\begin{equation} \label{eq:lmmse2}
\begin{aligned}
\text{Bmse}(\hat{\theta}) = \mathbb{E}\big[ (\theta-\hat{\theta})^2 \big]
\end{aligned}
\end{equation}
- $\mathbb{E}[\cdot]$ : $p(\mathbf{x}, \theta)$의 기대값
위 식을 최소화하는 최적의 추정값을 linear MMSE(LMMSE) 추정값이라고 한다. 위 식에서 $a_N$이 있다는 것에 주목하자. 이는 $\mathbf{x}, \theta$가 $0$이 아닌 평균을 가질 때 생성되는 값이다. 만약 두 확률 변수의 평균이 $0$인 경우 해당 항은 생략된다.
LMMSE 추정값을 결정하기 전에 이는 준최적(suboptimal) 추정값이라는 것을 기억해야 한다. 만약 MMSE 추정값이 선형이 아니라면 이는 최적(optimal) 추정값이 될 수 없다. LMMSE 추정값은 두 확률 변수 $\mathbf{x}, \theta$의 선형 상관 관계에 의존하기 때문에 만약 데이터 $\mathbf{x}$와 상관 관계가 없거나 비선형 상관 관계인 파라미터 $\theta$가 존재할 경우 이는 선형 추정값을 통해 예측할 수 없다. 다시 말하면 LMMSE 추정값은 반드시 존재하는 것은 아니다. 다음 예제를 통해 이를 확인해보자.
추정하고자 하는 파라미터 $\theta$를 단일 관측 데이터 $x[0]$로부터 찾고자 한다. 이 때, $x[0] \sim \mathcal{N}(0,\sigma^2)$을 따른다고 하자. 추정하고자 하는 파라미터가 $x[0]$의 제곱값이라고 하면 최적의 추정값은 아래와 같다.
\begin{equation}
\begin{aligned}
\hat{\theta} = x^2[0]
\end{aligned}
\end{equation}
따라서 BMSE 값은 $0$이 된다. 보다시피 추정값은 비선형 추정값이다. 만약 이 문제에 LMMSE 추정값을 찾는다고 해보자.
\begin{equation}
\begin{aligned}
\hat{\theta} = a_0 x[0] + a_1
\end{aligned}
\end{equation}
두 계수 $a_0,a_1$은 BMSE를 최소화함으로써 찾을 수 있다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbb{E}\big[ (\theta-\hat{\theta})^2 \big] \\
& = \mathbb{E} \big[ (\theta - a_0 x[0] - a_1)^2 \big]
\end{aligned}
\end{equation}
$a_0, a_1$에 대하여 각각 미분하고 $0$으로 놓으면 다음 식이 유도된다.
\begin{equation}
\begin{aligned}
& \mathbb{E} \big[ (\theta - a_0 x[0] - a_1)x[0] \big] = 0 \\
& \mathbb{E} \big[ (\theta - a_0 x[0] - a_1) \big] = 0 \\
\end{aligned}
\end{equation}
이를 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
& a_0 \mathbb{E}(x^2[0]) + a_1 \mathbb{E}(x[0]) = \mathbb{E}(\theta x[0]) \\
& a_0 \mathbb{E}(x[0]) + a_1 = \mathbb{E}(\theta)
\end{aligned}
\end{equation}
$\mathbb{E}(x[0])=0$이고 $\mathbb{E}(\theta x[0])= \mathbb{E}(x^3[0]) =0$이므로 계수는 다음과 같다.
\begin{equation}
\begin{aligned}
a_0 &=0 \\
a_1 &= \mathbb{E}(\theta) \\
& = \mathbb{E}(x^2[0]) \\
& = \sigma^2
\end{aligned}
\end{equation}
따라서 LMMSE 추정값은 $\hat{\theta} = \sigma^2$이 되고 이는 데이터 $x[0]$에 의존하지 않는다. 이는 $\theta$와 $x[0]$가 서로 상관 관계가 없기(uncorrelated) 때문이다. BMSE 값은 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbb{E}\big[ (\theta-\hat{\theta})^2 \big] \\
& = \mathbb{E} \big[ (\theta - \sigma^2)^2 \big] \\
& = \mathbb{E} \big[ (x^2[0] - \sigma^2)^2 \big] \\
& = \mathbb{E} \big[ x^4[0] - 2\sigma^2 \mathbb{E}(x^2[0]) + \sigma^4 \big] \\
& = 3\sigma^4 - 2\sigma^4 + \sigma^4 \\
& = 2\sigma^4
\end{aligned}
\end{equation}
비선형 추정값 $\hat{\theta}=x^2[0]$의 BMSE가 $0$이었던 것과 대조적으로 LMMSE 추정값은 값을 가진다. 따라서 LMMSE 추정값은 이러한 비선형 문제에 부적절한 것을 알 수 있다.
다시 본론으로 돌아와서 LMMSE에서 최적의 계수 $a_n$값을 찾아보자. (\ref{eq:lmmse1})를 (\ref{eq:lmmse2})에 넣고 미분을 수행하면 다음과 같은 식이 도출된다.
\begin{equation}
\begin{aligned}
\frac{\partial }{\partial a_N} \mathbb{E} \bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n] -a_N \theta \bigg)^2 \bigg] = -2\mathbb{E} \bigg[ \theta - \sum_{n=0}^{N-1}a_n x[n] -a_N \bigg]
\end{aligned}
\end{equation}
위 식을 $0$으로 놓고 풀면 다음과 같다.
\begin{equation}
\begin{aligned}
a_N = \mathbb{E}(\theta) - \sum_{n=0}^{N-1}a_n \mathbb{E}(x[n])
\end{aligned}
\end{equation}
앞서 말했듯이 $a_N$은 두 확률 변수의 평균이 모두 $0$이면 $a_N$ 또한 $0$이 된다. 수식 유도를 계속 이어가서 $a_N$을 (\ref{eq:lmmse2})에 대입해보자.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}) = \mathbb{E} \bigg\{ \bigg[ \sum_{n=0}^{N-1}a_n (x[n]-\mathbb{E}(x[n])) - (\theta - \mathbb{E}(\theta)) \bigg]^2 \bigg\}
\end{aligned}
\end{equation}
$\mathbf{a}=[a[0], a[1],\cdots,a_{N-1}]^{\intercal}$이라고 했을 때 위 식을 벡터 형태로 바꾸면 다음과 같다.
\begin{equation} \label{eq:lmmse5}
\begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbb{E} \big\{ \big[ \mathbf{a}^{\intercal}(\mathbf{x}-\mathbb{E}(\mathbf{x})) - (\theta - \mathbb{E}(\theta)) \big]^2 \big\} \\
& = \mathbb{E}[ \mathbf{a}^{\intercal}(\mathbf{x}-\mathbb{E}(\mathbf{x}))(\mathbf{x}-\mathbb{E}(\mathbf{x}))^{\intercal} \mathbf{a} ] - \mathbb{E}[ \mathbf{a}^{\intercal}(\mathbf{x}-\mathbb{E}(\mathbf{x}))(\theta - \mathbb{E}(\theta)) ] \\
& \quad\quad\quad\quad - \mathbb{E}[ (\theta - \mathbb{E}(\theta))(\mathbf{x}-\mathbb{E}(\mathbf{x}))^{\intercal}\mathbf{a} ] + \mathbb{E}[(\theta - \mathbb{E}(\theta))^2] \\
& = \mathbf{a}^{\intercal}\mathbf{C}_{xx}\mathbf{a} - \mathbf{a}^{\intercal}\mathbf{C}_{x\theta} - \mathbf{C}_{\theta x}\mathbf{a} + \mathbf{C}_{\theta\theta}
\end{aligned}
\end{equation}
- $\mathbf{C}_{xx} \in \mathbb{R}^{N \times N}$
- $\mathbf{C}_{\theta x} \in \mathbb{R}^{1 \times N}$
- $\mathbf{C}_{\theta \theta} \in \mathbb{R}^{1}$
BMSE를 $\mathbf{a}$에 대하여 미분하면 다음과 같다.
\begin{equation}
\begin{aligned}
\frac{\partial \text{Bmse}(\hat{\theta})}{\partial \mathbf{a}} = 2\mathbf{C}_{xx}\mathbf{a} - 2\mathbf{C}_{x \theta}
\end{aligned}
\end{equation}
위 식을 $0$으로 놓고 풀면 최적의 계수 $\mathbf{a}$를 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{a} = \mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta}
\end{aligned}
\end{equation}
이를 (\ref{eq:lmmse1})에 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{\theta} & = \mathbf{a}^{\intercal}\mathbf{x} + a_N \\
& = \mathbf{C}_{x\theta}^{\intercal}\mathbf{C}_{xx}^{-1}\mathbf{x} + \mathbb{E}(\theta) - \mathbf{C}_{x\theta}^{\intercal}\mathbf{C}_{xx}^{-1} \mathbb{E}(\mathbf{x})
\end{aligned}
\end{equation}
최종적으로 LMMSE 추정값은 다음과 같다.
\begin{equation} \label{eq:lmmse3}
\boxed{ \begin{aligned}
\hat{\theta} & = \mathbb{E}(\theta) + \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x}))
\end{aligned} }
\end{equation}
위 식은 MMSE 추정값 (\ref{eq:bay11})과 동일한 형태임에 주목하자. 이는 가우시안 분포에 대한 MMSE 추정값은 선형이 되어 선형 추정값의 조건을 자동으로 만족하기 때문이다. 만약 $\theta, \mathbf{x}$의 평균이 둘 다 $0$인 경우 $a_N$도 $0$이 되어 식은 다음과 같아진다.
\begin{equation}
\begin{aligned}
\hat{\theta} & = \mathbb{E}(\theta) + \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{x}
\end{aligned}
\end{equation}
위 식을 (\ref{eq:lmmse5})에 넣으면 BMSE는 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbf{C}_{x\theta}^{\intercal}\mathbf{C}_{xx}^{-1}\mathbf{C}_{xx}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} - \mathbf{C}_{x\theta}^{\intercal}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} - \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} + \mathbf{C}_{\theta\theta} \\
& = \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} - 2 \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} + \mathbf{C}_{\theta\theta}
\end{aligned}
\end{equation}
최종적으로 BMSE 다음과 같다.
\begin{equation} \label{eq:lmmse4}
\boxed{ \begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbf{C}_{\theta\theta} - \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta}
\end{aligned} }
\end{equation}
12.1.1. Example 12.1 - DC Level in WGN with Uniform Prior PDF
다음과 같은 데이터 모델이 주어졌다고 하자.
\begin{equation}
\begin{aligned}
x[n] = A+w[n] \quad n=0,1,\cdots,N-1
\end{aligned}
\end{equation}
- $w[n] \sim \mathcal{N}(0,\sigma^2)$ : WGN, $A$와 독립적(independent)
추정하고자 하는 파라미터 $A$는 균일 분포를 따른다고 하자($A\sim \mathcal{U}(-A_0,A_0)$). MMSE 추정값은 10.1 섹션에서 보았듯이 적분항이 포함되어 close form으로 구할 수 없었다. 이 문제에 LMMSE 추정값을 사용한다고 하자.
먼저 $\mathbb{E}(A)=0$이므로 $\mathbb{E}(x[n])=0$을 만족하는 것을 알 수 있다. 벡터 형태로 표현하면 $\mathbb{E}(\mathbf{x})=0$을 만족한다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{xx} & = \mathbb{E}(\mathbf{xx}^{\intercal}) \\
& = \mathbb{E}[ (A\mathbf{1}+\mathbf{w})(A\mathbf{1}+\mathbf{w})^{\intercal} ] \\
& = \mathbb{E}(A^2)\mathbf{11}^{\intercal} + \sigma^2 \mathbf{I} \\
\mathbf{C}_{\theta x} & = \mathbb{E}(A\mathbf{x}^{\intercal}) \\
& = \mathbb{E}[ A(A\mathbf{1}+\mathbf{w})^{\intercal} ] \\
& = \mathbb{E}(A^2)\mathbf{1}^{\intercal}
\end{aligned}
\end{equation}
- $\mathbf{1} \in \mathbb{R}^{N \times 1}$
(\ref{eq:lmmse3}) 식을 사용하여 LMMSE 추정값을 구하면 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{A} & = \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{x} \\
& = \sigma^2_A \mathbf{1}^{\intercal}(\sigma^2_A \mathbf{11}^{\intercal} + \sigma^2 \mathbf{I})^{-1} \mathbf{x}
\end{aligned}
\end{equation}
- $\sigma^2_A =\mathbb{E}(A^2)$
위 추정값은 Example 10.2에서 $\mu_A=0$으로 설정했을 때 추정값과 동일하다. 해당 예제에서 추정값을 가져오면 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{A} & = \frac{\sigma^2_A}{\sigma^2_A + \frac{\sigma^2}{N}} \bar{x}
\end{aligned}
\end{equation}
$\sigma^2_A =\mathbb{E}(A^2) = (2A_0)^2/12 = A_0^2/3$이므로 이를 대입하여 최종적인 LMMSE 추정값을 구하면 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{A} & = \frac{\frac{A_0^2}{3}}{\frac{A_0^2}{3} + \frac{\sigma^2}{N}} \bar{x}
\end{aligned}
\end{equation}
적분항이 포함되었던 MMSE 추정값과 달리 LMMSE 추정값은 closed form으로 구할 수 있다. 그리고 식에서 보다시피 $A$의 분포에 관계없이 해를 구할 수 있으며 오직 두 개의 모멘트(평균 $\bar{x}$과 분산 $\sigma^2$)만 알면 된다. 또한 $A$와 $\mathbf{w}$가 독립적이지(independence) 않아도 오직 상관 관계만 없으면(uncorrelated) 된다. 하지만 서두에서 말했듯이 LMMSE는 선형 제약조건이 들어간 suboptimal 추정값이며 MMSE 추정값이 최적 추정값임을 유의하자.
12.2. Geometrical Interpretations
챕터 8에서 least square estimator(LSE)를 기하학적으로 해석하여 벡터 공간에 대한 최소 거리를 찾는 문제임을 설명하였다. LMMSE 또한 이와 유사하게 기하학적으로 해석이 가능하다. 이 때 벡터는 확률 변수가 된다는 점이 챕터 8과 차이점이다. 기하학적 해석은 $\theta, \mathbf{x}$의 평균이 항상 $0$임을 가정한다. 만약 $0$이 아니라면 $\mathbf{x}'=\mathbf{x}- \mathbb{E}(\mathbf{x})$, $\theta'=\theta- \mathbb{E}(\theta)$ 와 같이 $0$으로 변환하여 $\theta'$을 추정하는 문제로 정의할 수 있다. LMMSE를 다시 보면 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{\theta} = \sum_{n=0}^{N-1}a_n x[n] + a_N
\end{aligned}
\end{equation}
이는 BMSE를 최소화함으로써 구할 수 있다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbb{E}\big[ (\theta-\hat{\theta})^2 \big] \\
& = \mathbb{E}\bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n] \bigg)^2 \bigg] \\
& = \| \theta - \sum_{n=0}^{N-1}a_n x[n] \|^2
& = \| \epsilon \|^2
\end{aligned}
\end{equation}
위 식을 보면 MSE를 최소화하는 것은 에러 벡터 $\epsilon=\theta-\hat{\theta}$의 L2-norm을 최소화하는 것과 동일하다.
LSE와 동일하게 파라미터 $\theta$는 데이터 벡터 $\mathbf{x}=[x[0],x[1],\cdots,x[N-1]]^{\intercal}$이 스팬하는 공간에 존재하지 않으므로 $\theta$와 $\mathbf{x}$가 스팬하는 공간의 최소 거리를 찾으면 이는 곧 최적해가 된다. 최소 거리는 평면에 수선의 발을 내림으로써 구할 수 있고 이는 곧 에러 벡터 $\epsilon=\theta-\hat{\theta}$가 된다.
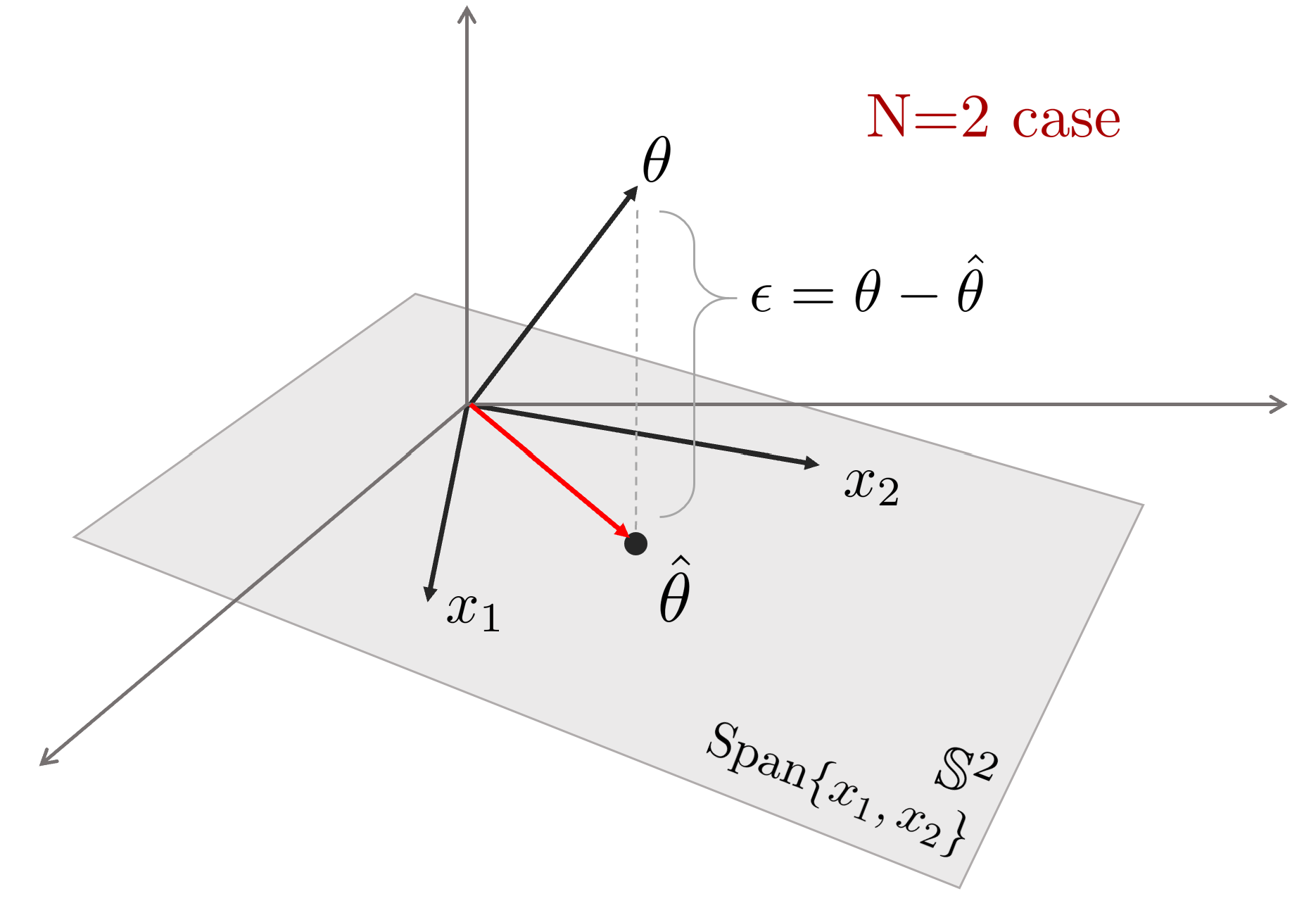
따라서 에러 벡터는 데이터 벡터 $\mathbf{x}$에 직교한다.
\begin{equation}
\begin{aligned}
\epsilon \perp x[0],x[1],\cdots,x[N-1]
\end{aligned}
\end{equation}
직교성(orthogonality)의 성질을 이용하면 다음과 같은 공식이 유도된다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbb{E} \big[ (\theta - \hat{\theta})x[n] \big] = 0 \quad n=0,1,\cdots,N-1
\end{aligned} }
\end{equation}
이를 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbb{E} \bigg[ \bigg( (\theta - \sum_{m=0}^{N-1}a_m x[m] \bigg)x[n] \bigg] =0 \quad n=0,1,\cdots,N-1 \\
& \text{ or } \quad \sum_{m=0}^{N-1}a_m \mathbb{E}(x[m]x[n]) = \mathbb{E}(\theta x[n]) \quad n=0,1,\cdots,N-1 \\
\end{aligned}
\end{equation}
행렬 형태로 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \begin{bmatrix} \mathbb{E}(x^2[0]) & \mathbb{E}(x[0]x[1]) & \cdots & \mathbb{E}(x[0]x[N-1]) \\
\mathbb{E}(x[0]x[1]) & \mathbb{E}(x^2[1]) & \cdots & \mathbb{E}(x[1]x[N-1]) \\
\vdots & \vdots & \ddots & \vdots \\
\mathbb{E}(x[N-1]x[0]) & \mathbb{E}(x[N-1]x[1]) & \cdots & \mathbb{E}(x^2[N-1]) \end{bmatrix} \begin{bmatrix} a_0 \\a_1\\ \vdots \\ a_N-1 \end{bmatrix} \\
& \quad\quad\quad\quad\quad\quad\quad\quad = \begin{bmatrix} \mathbb{E}(\theta x[0]) \\ \mathbb{E}(\theta x[1]) \\ \vdots \\ \mathbb{E}(\theta x[N-1]) \end{bmatrix}
\end{aligned}
\end{equation}
이는 정규 방정식 형태이다. 왼쪽 항을 $\mathbf{C}_{xx}$라고하고 오른쪽 항을 $\mathbf{C}_{x \theta}$라고 하면 위 식은 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{xx}\mathbf{a} = \mathbf{C}_{x \theta}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{a} = \mathbf{C}_{xx}^{-1}\mathbf{C}_{x \theta}
\end{aligned}
\end{equation}
따라서 LMMSE 추정값은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\hat{\theta} & = \mathbf{a}^{\intercal}\mathbf{x} \\
& = \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{x}
\end{aligned} }
\end{equation}
최소 BMSE 값은 $\mathbf{a}$를 대입하면 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}) & = \| \epsilon \|^2 \\
& = \| \theta - \sum_{n=0}^{N-1}a_n x[n] \|^2 \\
& = \mathbb{E}\bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n] \bigg)^2 \bigg] \\
& = \mathbb{E}\bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n] \bigg)\bigg( \theta - \sum_{m=0}^{N-1}a_m x[m] \bigg) \bigg] \\
& = \mathbb{E}\bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n] \bigg) \theta \bigg] - \mathbb{E}\bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n]\bigg)\sum_{m=0}^{N-1}a_m x[m] \bigg] \\
& = \mathbb{E}(\theta^2) - \sum_{n=0}^{N-1}a_n \mathbb{E}(x[n]\theta) - \underbrace{ \sum_{m=0}^{N-1}a_m \mathbb{E}\bigg[ \bigg( \theta - \sum_{n=0}^{N-1}a_n x[n] \bigg) x[m] \bigg]}_{=0}
\end{aligned}
\end{equation}
마지막 항은 직교성에 의해 $0$이 되어 소거된다. 이를 행렬 형태로 표현하면 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\text{Bmse}(\hat{\theta}) & = \mathbf{C}_{\theta\theta} - \mathbf{a}^{\intercal}\mathbf{C}_{x\theta} \\
& = \mathbf{C}_{\theta\theta} - \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta} \\
\end{aligned} }
\end{equation}
12.3. The Vector LMMSE Estimator
벡터 파라미터에 대한 LMMSE 추정값은 스칼라 파라미터 표현법을 단순히 확장한 것이다. 각각의 파라미터 $\theta_{i}$가 모두 BMSE를 최소화하는 추정값이 된다.
\begin{equation}
\begin{aligned}
\hat{\theta}_{i} = \sum_{n=0}^{N-1}a_{in} x[n] + a_{iN}
\end{aligned}
\end{equation}
- $i=1,2,\cdots,p$
최소화하고자 하는 BMSE는 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}_i) & = \mathbb{E}\big[ (\theta_i-\hat{\theta}_i)^2 \big] \\
\end{aligned}
\end{equation}
$i$번째 LMMSE 추정값은 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{\theta}_{i} & = \mathbb{E}(\theta_{i}) + \mathbf{C}_{\theta_i x}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x}))
\end{aligned}
\end{equation}
$i$번째 최소 BMSE 값은 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{\theta}_i) & = \mathbf{C}_{\theta_i\theta_i} - \mathbf{C}_{\theta_i x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta_i}
\end{aligned}
\end{equation}
스칼라 파라미터 $\theta_i$는 다음과 같이 벡터 형태로 쓸 수 있다.
\begin{equation}
\begin{aligned}
\hat{\boldsymbol{\theta}} & = \begin{bmatrix} \mathbb{E}(\theta_1) \\ \mathbb{E}(\theta_2) \\ \vdots \\ \mathbb{E}(\theta_p) \end{bmatrix} + \begin{bmatrix} \mathbf{C}_{\theta_1 x}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x})) \\
\mathbf{C}_{\theta_2 x}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x})) \\
\vdots \\
\mathbf{C}_{\theta_p x}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x}))
\end{bmatrix} \\
& = \begin{bmatrix} \mathbb{E}(\theta_1) \\ \mathbb{E}(\theta_2) \\ \vdots \\ \mathbb{E}(\theta_p) \end{bmatrix} + \begin{bmatrix} \mathbf{C}_{\theta_1 x} \\ \mathbf{C}_{\theta_2 x} \\ \vdots \\ \mathbf{C}_{\theta_p x} \end{bmatrix} \mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x})) \\\end{aligned}
\end{equation}
\begin{equation} \label{eq:lmmse6}
\boxed{ \begin{aligned}
\hat{\boldsymbol{\theta}} & = \mathbb{E}(\boldsymbol{\theta}) + \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}(\mathbf{x} - \mathbb{E}(\mathbf{x}))
\end{aligned} }
\end{equation}
- $\mathbf{C}_{\theta x} \in \mathbb{R}^{p\times N}$
BMSE도 행 형태로 표현하면 다음과 같다.
\begin{equation} \label{eq:lmmse7}
\boxed{ \begin{aligned}
\mathbf{M}_{\hat{\theta}} & = \mathbb{E}\big[ (\boldsymbol{\theta}-\hat{\boldsymbol{\theta}})(\boldsymbol{\theta}-\hat{\boldsymbol{\theta}})^{\intercal} \big] \\
& = \mathbf{C}_{\theta\theta} - \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x \theta}
\end{aligned} }
\end{equation}
- $\text{Bmse}(\hat{\theta}_i) = \big[\mathbf{M}_{\hat{\theta}} \big]_{ii}$
이렇듯 LMMSE의 벡터 파라미터 버전은 스칼라 파라미터를 단순 확장한 것이며 기존 LMMSE 성질과 동일하게 pdf의 첫 두 모멘트만 알면 추정값을 구할 수 있다. 마지막으로 LMMSE 추정값의 성질 중 유용한 성질 세 가지를 소개한다.
- LMMSE 추정값은 선형 변환(또는 affine)에 교환 법칙이 성립한다. 만약 $\boldsymbol{\alpha} = \mathbf{A}\boldsymbol{\theta}+\mathbf{b}$와 같은 선형 변환된 파라미터 $\boldsymbol{\alpha}$를 추정하고자 할 때 LMMSE 추정값은 $\hat{\boldsymbol{\alpha}} = \mathbf{A}\hat{\boldsymbol{\theta}}+\mathbf{b}$이 된다.
- 만약 서로 독립인 두 파라미터 $\boldsymbol{\theta}_1, \boldsymbol{\theta}_2$가 주어졌을 때 $\boldsymbol{\alpha} = \boldsymbol{\theta}_1 + \boldsymbol{\theta}_2$를 만족하는 $\boldsymbol{\alpha}$를 추정하고자 하는 경우 이는 $\hat{\boldsymbol{\alpha}} = \hat{\boldsymbol{\theta}}_1 + \hat{\boldsymbol{\theta}_2}$과 같이 쉽게 추정값을 찾을 수 있다.
- LMMSE 추정값은 MMSE 추정값이 선형이며 가우시안 분포를 따르는 경우와 동일한 추정값을 제공한다.
12.3.1. Theorem 12.1 (Bayesian Gauss-Markov Theorem)
만약 데이터가 베이지안 선형 모델로 다음과 같이 구성되어 있는 경우
\begin{equation}
\begin{aligned}
\mathbf{x} = \mathbf{H}\boldsymbol{\theta} + \mathbf{w}
\end{aligned}
\end{equation}
- $\mathbf{x} \in \mathbb{R}^{N\times 1}$
- $\mathbf{H} \in \mathbb{R}^{N\times p}$
- $\boldsymbol{\theta} \in \mathbb{R}^{p\times 1}$
- $\mathbf{w} \sim \mathcal{N}(0, \mathbf{C}_{w})$ : WGN, $\boldsymbol{\theta}$와 상관 관계 없음(uncorrelated)
LMMSE 추정값은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\hat{\boldsymbol{\theta}} & = \mathbb{E}(\boldsymbol{\theta}) + \mathbf{C}_{\theta\theta}\mathbf{H}^{\intercal}(\mathbf{H}\mathbf{C}_{\theta\theta}\mathbf{H}^{\intercal} + \mathbf{C}_{w})^{-1}(\mathbf{x} - \mathbf{H}\mathbb{E}(\boldsymbol{\theta})) \\
& = \mathbb{E}(\boldsymbol{\theta}) + (+ \mathbf{C}_{\theta\theta}^{-1} + \mathbf{H}\mathbf{C}_{w}^{-1}\mathbf{H}^{\intercal})^{-1}\mathbf{H}^{\intercal}\mathbf{C}_{w}^{-1}(\mathbf{x} - \mathbf{H}\mathbb{E}(\boldsymbol{\theta})) \\
\end{aligned} }
\end{equation}
추정값의 성능은 에러 벡터 $\boldsymbol{\epsilon} = \boldsymbol{\theta} - \hat{\boldsymbol{\theta}}$를 평가함으로써 알 수 있다. 에러 벡터는 $\boldsymbol{\epsilon} = \sim \mathcal{N}(0, \mathbf{C}_{\epsilon})$을 따른다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{\epsilon} & = \mathbb{E}_{x,\theta}(\boldsymbol{\epsilon}\boldsymbol{\epsilon}^{\intercal}) \\
& = \mathbf{C}_{\theta\theta} - \mathbf{C}_{\theta\theta}\mathbf{H}^{\intercal}(\mathbf{H}\mathbf{C}_{\theta\theta}\mathbf{H}^{\intercal} + \mathbf{C}_{w})^{-1}\mathbf{H}\mathbf{C}_{\theta\theta} \\
& = (\mathbf{C}_{\theta\theta}^{-1} + \mathbf{H}\mathbf{C}_{w}^{-1}\mathbf{H}^{\intercal} )^{-1}
\end{aligned}
\end{equation}
에러 벡터의 공분산 $\mathbf{C}_{\epsilon}$은 또한 최소 BMSE 값을 의미한다.
\begin{equation}
\begin{aligned}
\big[\mathbf{M}_{\hat{\theta}} \big]_{ii} & = \big[\mathbf{C}_{\epsilon} \big]_{ii} \\
& = \text{Bmse}(\hat{\theta}_i)
\end{aligned}
\end{equation}
12.4. Sequential LMMSE Estimation
챕터 8에서 새로운 데이터가 들어올 때마다 LS 추정값을 업데이트하는 sequential LS에 대해 학습하였다. 동일한 과정을 LMMSE 추정값에 대해서도 수행할 수 있다. Example 10.1 문제를 다시 살펴보자.
\begin{equation}
\begin{aligned}
x[n]=A+w[n] \quad n=0,1,\cdots,N-1
\end{aligned}
\end{equation}
- $A \sim \mathcal{N}(\mu_A, \sigma_A^2)$
- $w[n] \sim \mathcal{N}((0, \sigma^2)$ : WGN
MMSE 추정값은 (\ref{eq:bay9})과 같다.
\begin{equation}
\begin{aligned}
\hat{A}[N-1] = \frac{\sigma^2_A}{\sigma^2_A + \frac{\sigma^2}{N}} \bar{x}
\end{aligned}
\end{equation}
MMSE 추정값은 가우시안 케이스에 한하여 LMMSE과 동일한 값을 가지기 때문에 $\hat{A}[N-1]$는 데이터 $\{ x[0],x[1],\cdots, x[N-1]]\}$이 관측되었을 때 LMMSE 추정값을 의미한다. BMSE를 보면 다음과 같다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}[N-1]) = \frac{\sigma^2_A \sigma^2}{N\sigma^2_A + \sigma^2} \end{aligned}
\end{equation}
Sequential LMMSE는 위와 같은 상황에서 데이터 $x[n]$이 관측되었을 때 $\hat{A}[N]$ 값을 구하는 것이 목표이다. $\hat{A}[N]$를 정의에 따라 전개해보면 아래와 같다.
\begin{equation}
\begin{aligned}
\hat{A}[N] & = \frac{\sigma^2_A}{\sigma^2_A + \frac{\sigma^2}{N+1}} \frac{1}{N+1} \sum_{n=0}^{N-1}x[n] \\
& = \frac{N\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} \frac{1}{N} \bigg( \sum_{n=0}^{N-1}x[n] + x[N] \bigg) \\
& = \frac{N\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} \frac{\sigma_A^2+\frac{\sigma^2}{N}}{\sigma^2_A} \hat{A}[N-1] + \frac{\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} x[N] \\
& = \frac{N\sigma^2_A + \sigma^2}{(N+1)\sigma^2_A + \sigma^2} \hat{A}[N-1] + \frac{\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} x[N] \\
& = \hat{A}[N-1] + \bigg( \frac{N\sigma^2_A + \sigma^2}{(N+1)\sigma^2_A + \sigma^2} -1 \bigg) \hat{A}[N-1] + \frac{\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} x[N] \\
& = \hat{A}[N-1] + \frac{\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} (x[N] - \hat{A}[N-1])
\end{aligned}
\end{equation}
Sequential LS와 유사하게 새로운 관측 데이터 $x[N]$이 들어오면 기존 $\hat{A}[N-1]$ 값은 $(x[N] - \hat{A}[N-1])$에 게인 값이 적용된 상태로 업데이트된다. 게인 값을 자세히 보면 다음과 같다.
\begin{equation}
\begin{aligned}
K[N] & = \frac{\sigma^2_A}{(N+1)\sigma^2_A + \sigma^2} \\
& = \frac{\text{Bmse}(\hat{A}[N-1])}{\text{Bmse}(\hat{A}[N-1]) + \sigma^2}
\end{aligned}
\end{equation}
게인 값은 $N\rightarrow \infty$로 감에 따라 $0$으로 수렴한다. BMSE 값 또한 다음과 같이 업데이트된다.
\begin{equation}
\begin{aligned}
\text{Bmse}(\hat{A}[N]) & = \frac{\sigma^2_A \sigma^2}{(N+1)\sigma^2_A + \sigma^2} \\
& = \frac{N\sigma^2_A + \sigma^2}{(N+1)\sigma^2_A + \sigma^2} \frac{\sigma^2_A \sigma}{N\sigma^2_A + \sigma^2} \\
& = (1-K[N]) \text{Bmse}(\hat{A}[N-1])
\end{aligned}
\end{equation}
이를 정리하면 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
& \textbf{Estimator Update: } \\
& \quad \hat{A}[N] = \hat{A}[N-1] + K[N](x[N] - \hat{A}[N-1]) \\
& \text{where, } \\
& \quad \mathbf{K}[N]= \frac{\text{Bmse}(\hat{A}[N-1])}{\text{Bmse}(\hat{A}[N-1]) + \sigma^2} \\
& \textbf{Variance Update: } \\
& \quad \text{Bmse}(\hat{A}[N]) = \quad(1-K[N]) \text{Bmse}(\hat{A}[N-1])
\end{aligned} }
\end{equation}
12.5 Signal Processing Examples - Wiener Filtering
이번 섹션에서는 LMMSE 추정값이 실제 사용되는 응용 알고리즘에 대하여 설명한다. 만약 데이터 $\{x[0], x[1], \cdots, x[N-1]\}$이 WSS(wide-sense stationary)이고 평균이 $0$이고 가정해보자. 그렇다면 공분산 행렬 $\mathbf{C}_{xx}$은 다음과 같은 대칭 퇴플리츠(symmetric Toeplitz) 행렬이 된다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{xx} & = \begin{bmatrix}
\mathbf{r}_{xx}[0] & \mathbf{r}_{xx}[1] & \cdots & \mathbf{r}_{xx}[N-1] \\
\mathbf{r}_{xx}[1] & \mathbf{r}_{xx}[0] & \cdots & \mathbf{r}_{xx}[N-2] \\
\vdots & \vdots& \ddots & \vdots \\
\mathbf{r}_{xx}[N-1] & \mathbf{r}_{xx}[N-2] & \cdots & \mathbf{r}_{xx}[0] \\
\end{bmatrix} \\
& = \mathbf{R}_{xx}
\end{aligned}
\end{equation}
- $\mathbf{r}_{xx}[k]$: $x[n]$의 ACF(auto-corrleation function)
- $\mathbf{R}_{xx}$: autocorrelation 행렬
그리고 추정하고자 하는 파라미터 $\boldsymbol{\theta}$는 평균이 $0$인 분포를 따르고 있다고 가정하자. 위와 같은 가정이 주어졌을 때 다음의 여러가지 응용 방법들을 통틀어서 위너 필터(Wiener filter)이라고 부른다.
- Filtering : 필터링은 데이터 모델이 $x[m]=s[m]+w[m]$일 때 추정하고자 하는 파라미터가 $\theta=s[n]$인 경우를 말한다. $s[n]$은 신호를 의미하며 $w[n]$은 노이즈를 의미한다. 최적의 파라미터를 추정함으로써 우리는 신호에서 노이즈를 필터링하고자 한다. 필터링에서는 파라미터가 현재와 과거 데이터에만 의존하는 것에 유의하자.}
- Smoothing: 스무딩은 데이터 모델이 $x[n]=s[n]+w[n]$이고 $n$개의 관측 데이터 $\{x[0],x[1],\cdots,x[N-1]\}$이 주어졌을 때 $\theta=s[n]$을 추정하는 경우를 말한다. 예를 들어 $s[1]$을 추정하기 위해 모든 관측 데이터 $\{x[0],x[1],\cdots,x[N-1]\}$가 사용된다. 당연하게도 스무딩은 모든 데이터가 관측되기 전에는 수행할 수 없다.
- Prediction: 예측은 관측 데이터 $\{x[0],x[1],\cdots,x[N-1]\}$가 주어졌을 때 $\theta = x[N-1+l]$을 추정하는 경우를 말한다. 이 때, $l$은 임의의 양수이다.
- Interpolation: 보간은 관측 데이터 $\{x[0], \cdots ,x[n-1], x[n+1,\cdots,x[N-1]\}$이 주어졌을 떄 $\theta=x[n]$을 추정하는 경우를 말한다.

위너 필터는 선형 시스템에서 잡음이 포함된 신호를 필터링하여 원래의 신호를 추정하기 위한 최적의 선형 필터이다. 이는 정상적(stationary) 신호와 잡음을 가정하며, 주어진 신호에 대한 평균 제곱 오차를 최소화(=LMMSE)하는 필터 계수를 찾는 문제로 정의된다. 위너 필터는 시간 도메인 또는 주파수 도메인에서 구현될 수 있으며, 고정된 선형 시스템에서 사용된다.
위너 필터 추정값을 구하기 위해 벡터 LMMSE 추정값 (\ref{eq:lmmse6})과 BMSE (\ref{eq:lmmse7})를 사용한다.
\begin{equation} \label{eq:lmmse8}
\begin{aligned}
\hat{ \boldsymbol{\theta}} = \mathbf{C}_{\theta x}\mathbf{C}^{-1}_{xx} \mathbf{x}
\end{aligned}
\end{equation}
- $\mathbb{E}(\boldsymbol{\theta})=\mathbb{E}(\mathbf{x})=0$ : 앞서 가정에 따라 두 기대값은 $0$이 된다.
\begin{equation} \label{eq:lmmse9}
\begin{aligned}
\mathbf{M}_{\hat{\theta}} = \mathbf{C}_{\theta\theta} - \mathbf{C}_{\theta x}\mathbf{C}_{xx}^{-1}\mathbf{C}_{x\theta}
\end{aligned}
\end{equation}
12.5.1. Smoothing
스무딩 문제는 관측 데이터 $\mathbf{x} = [x[0],x[1],\cdots,x[N-1]]^{\intercal}$가 주어졌을 때 $\boldsymbol{\theta} = \mathbf{s} = [s[0],s[1],\cdots,s[N-1]]^{\intercal}$을 추정하는 문제를 말한다. 신호 $\mathbf{s}$와 노이즈 $\mathbf{w}$가 서로 상관관계가 없다고(uncorrelated) 가정하면 ACF는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{r}_{xx}[k] = \mathbf{r}_{ss}[k] + \mathbf{r}_{ww}[k]
\end{aligned}
\end{equation}
따라서 공분산 행렬은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{xx} = \mathbf{R}_{xx} = \mathbf{R}_{ss} + \mathbf{R}_{ww}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{C}_{\theta x} = \mathbb{E}(\mathbf{sx}^{\intercal}) = \mathbb{E}(\mathbf{s}(\mathbf{s}+\mathbf{w})^{\intercal}) = \mathbf{R}_{ss}
\end{aligned}
\end{equation}
이를 (\ref{eq:lmmse8})에 대입하면 스무딩의 대한 위너 추정값은 다음과 같다.
\begin{equation} \boxed{
\begin{aligned}
\hat{\mathbf{s}}& = \mathbf{R}_{ss}(\mathbf{R}_{ss}+\mathbf{R}_{ww})^{-1}\mathbf{x} \\
& = \mathbf{Wx}
\end{aligned} }
\end{equation}
- $\mathbf{W} =\mathbf{R}_{ss}(\mathbf{R}_{ss}+\mathbf{R}_{ww})^{-1}$: Wiener smoothing 행렬이라고 한다.
이를 (\ref{eq:lmmse9})에 대입하면 스무딩의 대한 BMSE는 다음과 같다.
\begin{equation} \boxed{
\begin{aligned}
\mathbf{M}_{\hat{\mathbf{s}}} & = \mathbf{R}_{ss} - \mathbf{R}_ss(\mathbf{ss}+\mathbf{R}_{ww})^{-1}\mathbf{R}_{ss} \\
& = (\mathbf{I} - \mathbf{W})\mathbf{R}_{ss}
\end{aligned} }
\end{equation}
12.5.2. Filtering
필터링 문제는 관측 데이터 $\mathbf{x}=[x[0],x[1],\cdots,x[n]]^{\intercal}$가 주어졌을 때 $\theta=s[n]$을 추정하는 문제를 말한다. 스무딩과 마찬가지로 신호 $\mathbf{s}$와 노이즈 $\mathbf{w}$가 서로 상관관계가 없다고(uncorrelated) 가정하면 ACF는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{xx} = \mathbf{R}_{xx} = \mathbf{R}_{ss} + \mathbf{R}_{ww}
\end{aligned}
\end{equation}
$\mathbf{R}_{ss},\mathbf{R}_{ww}$는 $(n+1)\times (n+1)$ 크기의 auto-correlation 행렬이다. 공분산행렬은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{\theta x} & = \mathbb{E}(s[n] [ x[0] \quad x[1] \quad \cdots \quad x[n]] ) \\
& = \mathbb{E}(s[n] [ s[0] \quad s[1] \quad \cdots \quad s[n]] ) \\
& = [\mathbf{r}_{ss}[n] \mathbf{r}_{ss}[n-1] \cdots \mathbf{r}_{ss}[0]] \\
&= \mathbf{r}_{ss}'^{\intercal}
\end{aligned}
\end{equation}
이를 (\ref{eq:lmmse8})에 대입하면 필터링에 대한 위너 추정값은 다음과 같다.
\begin{equation}
\begin{aligned}
\hat{s}[n]& = \mathbf{r}_{ss}'^{\intercal}( \mathbf{R}_{ss} +\mathbf{R}_{ww} )^{-1}\mathbf{x}
\end{aligned}
\end{equation}
$(n+1)\times n$ 크기의 가중치 벡터를 $\mathbf{a}=(\mathbf{R}_{ss}+\mathbf{R}_{ww})^{-1}\mathbf{r}_{ss}'$라고 정의하면 위 식은 다음과 같이 쓸 수 있다.
\begin{equation} \label{eq:lmmse11}
\boxed{ \begin{aligned}
\hat{s}[n]& = \mathbf{a}^{\intercal}\mathbf{x}
\end{aligned} }
\end{equation}
- $\mathbf{a} = [a_0 \ a_1 \ \cdots \ a_n]^{\intercal}$
이는 스칼라 파라미터에 대한 LMMSE (\ref{eq:lmmse1})와 형태가 동일하다. 우리는 $n$이 증가할 때마다 새로운 추정값을 계산하는 과정을 시변 임펄스 응답(time-varying impulse response) $h^{(n)}[k]$를 정의함으로써 시스템의 필터링 문제로 해석할 수 있다. $h^{(n)}[k]$를 $k$ 샘플 전에 적용된 임펄스에 대한 시간 $n$에서 응답으로 정의한다.
\begin{equation}
\begin{aligned}
h^{(n)}[k] = a_{n-k} \quad k=0,1,\cdots,n
\end{aligned}
\end{equation}
위와 같이 정의하면 (\ref{eq:lmmse11})은 다음과 같이 변형된다.
\begin{equation}
\begin{aligned}
\hat{s}[n] & = \sum_{k=0}^{n}a_k x[k] \\
& = \sum_{k=0}^{n}h^{(n)} [n-k]x[k] \quad \text{ or} \\
& = \sum_{k=0}^{n}h^{(n)} [k]x[n-k]
\end{aligned}
\end{equation}
위 식은 시변(time-varying) FIR 필터의 형태인 것을 알 수 있다. 임펄스 응답 $\mathbf{h}$를 찾기 위해 $\mathbf{a}$를 살펴보자.
\begin{equation}
\begin{aligned}
& (\mathbf{R}_{ss}+\mathbf{R}_{ww})\mathbf{a} = \mathbf{r}'_{ss} \\
& \rightarrow (\mathbf{R}_{ss}+\mathbf{R}_{ww})\mathbf{h} = \mathbf{r}_{ss} \\
\end{aligned}
\end{equation}
- $\mathbf{r}_{ss} = [r_{ss}[0]r_{ss}[1]\cdots r_{ss}[n]]^{\intercal}$
대칭 퇴플리츠(symmetric Toeplitz) 행렬의 특성으로 인해 $\mathbf{h}$는 단순히 $\mathbf{a}$ 행렬의 순서를 위아래로 뒤집음(flipped upside down)으로써 얻을 수 있다.
\begin{equation}
\begin{aligned}
\begin{bmatrix}
r_{xx}[0] & r_{xx}[1] & \cdots & r_{xx}[n] \\
r_{xx}[1] & r_{xx}[0] & \cdots & r_{xx}[n-1] \\
\vdots & \vdots & \ddots & \vdots \\
r_{xx}[n] & r_{xx}[n-1] & \cdots & r_{xx}[0] \\
\end{bmatrix}
\begin{bmatrix}
h^{(n)}[0] \\ h^{(n)}[1] \\ \vdots \\ h^{(n)}[n]
\end{bmatrix}
\begin{bmatrix}
r_{ss}[0] \\ r_{ss}[1] \\ \vdots \\ r_{ss}[n]
\end{bmatrix}
\end{aligned}
\end{equation}
- $r_{xx}[k] = r_{ss}[k] + r_{ww}[k]$
위 식을 위너-호프 방정식(Wiener-Hopf equation)이라고 한다. 위너-호프 방정식은 정상(stationary) 랜덤 프로세스에 대해 최적의 필터 계수 $h^{(n)}[k]$를 결정하기 위해 사용된다. 결과적으로, 위너 필터는 주어진 입력 신호에 대해 오차를 최소화하는 출력 $\hat{s}[n]$을 생성한다.
Wrap up















References
 A L I D A
A L I D A





