본 포스트는 필자가 Kalman filter 공부하면서 배운 내용을 정리한 포스트이다.
이전 포스팅 칼만 필터(Kalman filter) 개념 정리 Part 1에서 더 많은 내용을 확인할 수 있다.
Kalman filter를 이해하는데 필요한 기반 지식은 확률 이론(Probability Theory) 개념 정리 포스팅을 참조하면 된다.
Particle filter에 대해 알고 싶으면 파티클 필터(Particle Filter) 개념 정리 포스팅을 참조하면 된다.
arXiv preprint
English version
Notes on Kalman Filter (KF, EKF, ESKF, IEKF, IESKF)
The Kalman Filter (KF) is a powerful mathematical tool widely used for state estimation in various domains, including Simultaneous Localization and Mapping (SLAM). This paper presents an in-depth introduction to the Kalman Filter and explores its several e
arxiv.org
Derivation of Kalman filter
본 섹션에서는 칼만 필터의 prediction 스텝과 update 스텝의 수식 유도 과정에 대해 설명한다. 대부분의 내용은 \ref{ref:13}의 3.2.4 "Mathematical Derivation of the KF" 섹션을 참조하여 작성하였다.
칼만 필터는 $\text{bel}(\mathbf{x}_{t}), \overline{\text{bel}}(\mathbf{x}_{t})$가 모두 가우시안 분포를 따른다고 가정하므로 각각 평균 $\hat{\mathbf{x}}_t$와 공분산 $\mathbf{P}$를 구할 수 있다.
\begin{equation}
\begin{aligned}
& \overline{\text{bel}}(\mathbf{x}_{t}) = \int {\color{Red} p(\mathbf{x}_{t} \ | \ \mathbf{x}_{t-1}, \mathbf{u}_{t}) } \text{bel}(\mathbf{x}_{t-1}) d \mathbf{x}_{t-1} \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1}) \\
& \text{bel}(\mathbf{x}_{t}) = \eta \cdot {\color{Cyan} p( \mathbf{z}_{t} \ | \ \mathbf{x}_{t}) } \overline{\text{bel}}(\mathbf{x}_{t}) \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t}, \mathbf{P}_{t|t})
\end{aligned}
\end{equation}
(\ref{eq:kf0})의 모션 모델과 관측 모델로부터 ${\color{Red} p(\mathbf{x}_{t} \ | \ \mathbf{x}_{t-1}, \mathbf{u}_{t}) } ,{\color{Cyan} p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t})}$
는 (\ref{eq:kf1}), (\ref{eq:kf2}) 같이 나타낼 수 있음을 보였다. (pdf은 정상적으로 reference가 나온다)
\begin{equation}
\begin{aligned}
& {\color{Red} p(\mathbf{x}_{t} \ | \ \mathbf{x}_{t-1}, \mathbf{u}_{t}) }&& \sim \mathcal{N}(\mathbf{F}_{t}\mathbf{x}_{t-1} + \mathbf{B}_{t}\mathbf{u}_{t}, \mathbf{Q}_{t}) \\
& && = \frac{1}{ \sqrt{\text{det}(2\pi \mathbf{Q}_t)}}\exp\bigg( -\frac{1}{2}(\mathbf{x}_{t} -\mathbf{F}_{t}\mathbf{x}_{t-1}-\mathbf{B}_{t}\mathbf{u}_t)^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{x}_{t}-\mathbf{F}_{t}\mathbf{x}_{t-1}-\mathbf{B}_{t}\mathbf{u}_{t}) \bigg)\\
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& {\color{Cyan} p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t}) } && \sim \mathcal{N}(\mathbf{H}_{t}\mathbf{x}_{t}, \mathbf{R}_{t}) \\
& && = \frac{1}{ \sqrt{\text{det}(2\pi \mathbf{R}_t)}}\exp\bigg( -\frac{1}{2}(\mathbf{z}_{t}-\mathbf{H}_{t}\mathbf{x}_{t})^{\intercal}\mathbf{R}_{t}^{-1}(\mathbf{z}_{t}-\mathbf{H}_{t}\mathbf{x}_{t}) \bigg)
\end{aligned}
\end{equation}
Derivation of KF prediction step
먼저 $\overline{\text{bel}}(\mathbf{x}_{t})$ 수식을 유도해보자. $\overline{\text{bel}}(\mathbf{x}_{t})$에서 구하고자 하는 평균과 분산은 다음과 같다.
\begin{equation}
\begin{aligned}
& \underbrace{\overline{\text{bel}}(\mathbf{x}_{t})}_{\sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1}) } = \int \underbrace{ p(\mathbf{x}_{t} \ | \ \mathbf{x}_{t-1}, \mathbf{u}_{t}) }_{\sim \mathcal{N}(\mathbf{F}_t\mathbf{x}_{t-1}+\mathbf{B}_t \mathbf{u}_t, \mathbf{R}_{t})} \underbrace{\text{bel}(\mathbf{x}_{t-1})}_{\quad \sim \mathcal{N}(\hat{\mathbf{x}}_{t-1}, \mathbf{P}_{t-1})} d \mathbf{x}_{t-1} \end{aligned}
\end{equation}
위 식을 가우시안 분포 형태로 펼쳐보면 다음과 같다.
\begin{equation}
\begin{aligned}
& \overline{\text{bel}}(\mathbf{x}_{t}) = \eta \int \exp \Big(-\frac{1}{2}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1}-\mathbf{B}_t\mathbf{u}_t)^{\intercal} \mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1}-\mathbf{B}_t\mathbf{u}_t) \Big) \\
& \qquad\qquad\qquad\qquad \cdot \exp \Big( -\frac{1}{2}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1})^{\intercal} \mathbf{P}_{t-1}^{-1}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1}) \Big) d \mathbf{x}_{t-1} \end{aligned}
\end{equation}
위 식은 다음과 같이 더 간단하게 치환할 수 있다.
\begin{equation}
\begin{aligned}
& \overline{\text{bel}}(\mathbf{x}_{t}) = \eta \int \exp(- {\color{Mahogany} \mathbf{L}_{t} } ) d \mathbf{x}_{t-1} \end{aligned}
\end{equation}
\begin{equation} \label{eq:derivkf1}
\boxed{ \begin{aligned}
& \text{where, } {\color{Mahogany} \mathbf{L}_t }= \frac{1}{2}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1}-\mathbf{B}_t\mathbf{u}_t)^{\intercal} \mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1}-\mathbf{B}_t\mathbf{u}_t) \\
& \qquad\qquad\qquad + \frac{1}{2}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1})^{\intercal} \mathbf{P}_{t-1}^{-1}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1})
\end{aligned} }
\end{equation}
$\mathbf{L}_t$를 자세히 살펴보면 $\mathbf{x}_t, \mathbf{x}_{t-1}$에 대한 2차식 형태(=quadratic)를 가짐을 알 수 있다. $\overline{\text{bel}}(\mathbf{x}_{t})$는 적분 $\int$ 연산을 포함하고 있으므로 적분 연산에서 closed form 솔루션을 얻으려면 $\mathbf{L}_t$를 적분 연산 밖으로 빼는 작업이 필요하다. 이를 위해 $\mathbf{L}_t$를 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$와 $\mathbf{L}_t(\mathbf{x}_t)$ 항으로 분리한다.
\begin{equation}
\begin{aligned}
\mathbf{L}_t = \mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) + \mathbf{L}_t(\mathbf{x}_t)
\end{aligned}
\end{equation}
$\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$는 $\mathbf{x}_{t-1}$ 항이 포함되어 있는 항들을 전부 포함하며 $\mathbf{L}_t(\mathbf{x}_t)$는 오직 $\mathbf{x}_t$만 있는 항을 포함한다. 이를 통해 $\mathbf{L}_t(\mathbf{x}_t)$는 $\mathbf{x}_{t-1}$에 독립이 되어 적분 $\int$ 기호 밖으로 빼낼 수 있다.
\begin{equation} \label{eq:derivkf4}
\begin{aligned}
\overline{\text{bel}}(\mathbf{x}_{t}) & = \eta \int \exp(-\mathbf{L}_{t}) d \mathbf{x}_{t-1} \\
& = \eta \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) - {\color{Mahogany} \mathbf{L}_t(\mathbf{x}_t) } ) d \mathbf{x}_{t-1} \\
& = \eta \exp(-{\color{Mahogany} \mathbf{L}_t(\mathbf{x}_t) } ) \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)) d \mathbf{x}_{t-1}
\end{aligned}
\end{equation}
다음으로 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$를 $\mathbf{x}_{t}$에 대해 독립이 되도록 설정하여 적분 $\int$ 내부의 값이 상수(=constant)가 되도록 해야한다. $\mathbf{x}_{t}$에 독립인 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$을 분해(decompose)하기 위해 우선 $\mathbf{L}_t$를 $\mathbf{x}_{t-1}$에 대해 편미분을 수행한다.
\begin{equation} \label{eq:derivkf2}
\begin{aligned}
\frac{\partial \mathbf{L}_t}{\partial \mathbf{x}_{t-1}} = -\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1} - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1})
\end{aligned}
\end{equation}
\begin{equation} \label{eq:derivkf3}
\begin{aligned}
\frac{\partial^2 \mathbf{L}_t}{\partial \mathbf{x}^2_{t-1}} = \mathbf{F}^{\intercal}_t\mathbf{R}_t^{-1} \mathbf{F}_t+ \mathbf{P}_{t-1}^{-1} := \Psi_t^{-1}
\end{aligned}
\end{equation}
- $\Psi_t^{-1}$ : $\mathbf{L}_t$의 곡률(curvature)를 의미하며 공분산의 역행렬을 의미한다.
(\ref{eq:derivkf1})에서 보다시피 $\mathbf{L}_t$는 이차식(quadratic) 형태이며 공분산 행렬에 의해 Positive semi-definite을 만족하므로 $\mathbf{x}_{t-1}$로 1차 편미분 후 0이 되는 값은 $\mathbf{x}_{t-1}$에 대한 평균, 2차 편미분 값은 $\mathbf{x}_{t-1}$에 대한 공분산의 역행렬이 된다.
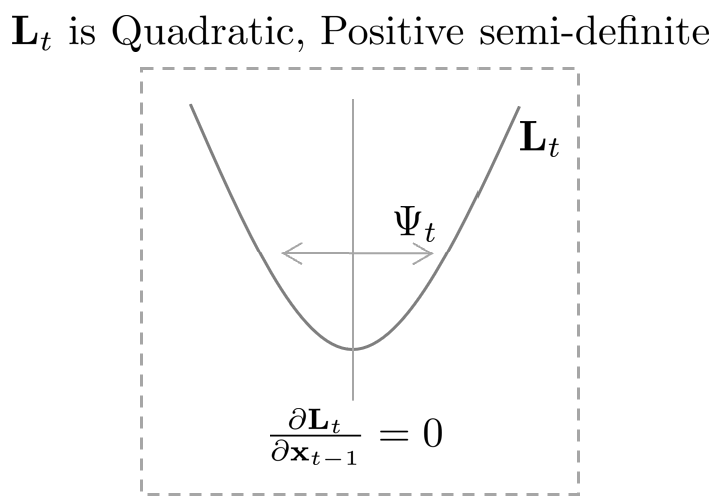
우선 1차 편미분한 (\ref{eq:derivkf2})을 0으로 설정한 후 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{F}_t {\color{Cyan} \mathbf{x}_{t-1} } - \mathbf{B}_t \mathbf{u}_t) = \mathbf{P}_{t-1}^{-1}({\color{Cyan} \mathbf{x}_{t-1} } - \hat{\mathbf{x}}_{t-1})
\end{aligned}
\end{equation}
위 식을 ${\color{Cyan} \mathbf{x}_{t-1} }$에 대해 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \Leftrightarrow \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) - \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t {\color{Cyan} \mathbf{x}_{t-1} } = \mathbf{P}_{t-1}^{-1}{\color{Cyan} \mathbf{x}_{t-1} } - \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} \\
& \Leftrightarrow \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t {\color{Cyan} \mathbf{x}_{t-1} }+ \mathbf{P}_{t-1}^{-1}{\color{Cyan} \mathbf{x}_{t-1} } = \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} \\
& \Leftrightarrow (\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1}){\color{Cyan} \mathbf{x}_{t-1} } = \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}\\
& \Leftrightarrow \Psi_t^{-1}{\color{Cyan} \mathbf{x}_{t-1} } = \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} \\
& \Leftrightarrow {\color{Cyan} \mathbf{x}_{t-1} } = \Psi_t[ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} ]
\end{aligned}
\end{equation}
지금까지 구한 ${\color{Cyan} \mathbf{x}_{t-1}}$을 통해 $\mathbf{L}_t$에서 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$을 다음과 같이 2차식 형태로 분해(decompose)할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
&\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) = \frac{1}{2}(\mathbf{x}_{t-1} - { \Psi_t[ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} ] })^{\intercal} \Psi^{-1} \\
&\qquad\qquad\qquad\qquad (\mathbf{x}_{t-1} - { \Psi_t[ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} ] } )
\end{aligned} }
\end{equation}
이는 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$ 부분만을 분해(decompose)한 것으로 유일한 해는 아님에 유의한다. $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$을 $\exp(\cdot)$ 내부에 넣으면 다음과 같이 가우시안 분포 형태로 정의할 수 있다.
\begin{equation}
\begin{aligned}
\det(2\pi \Psi)^{-\frac{1}{2}} \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t))
\end{aligned}
\end{equation}
가우시안 분포이므로 모든 영역에 대한 넓이의 합은 1이 된다.
\begin{equation}
\begin{aligned}
\int \det(2\pi \Psi)^{-\frac{1}{2}} \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)) d\mathbf{x}_{t-1} = 1
\end{aligned}
\end{equation}
위 식을 정리하면 다음과 같다.
\begin{equation}
\begin{aligned}
{\color{Mahogany} \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)) d\mathbf{x}_{t-1} } = \det(2\pi \Psi)^{\frac{1}{2}}
\end{aligned}
\end{equation}
위 식을 통해 앞서 설명했던 (\ref{eq:derivkf4})에서 적분 항이 상수(constant)가 되는 것을 확인할 수 있다.
\begin{equation}
\begin{aligned}
\overline{\text{bel}}(\mathbf{x}_{t}) & = \eta \int \exp(-\mathbf{L}_{t}) d \mathbf{x}_{t-1} \\
& = \eta \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) - \mathbf{L}_t(\mathbf{x}_t)) d \mathbf{x}_{t-1} \\
& = \eta \exp(-\mathbf{L}_t(\mathbf{x}_t)) {\color{Mahogany} \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)) d \mathbf{x}_{t-1} } \\
& = \eta' \exp(-\mathbf{L}_t(\mathbf{x}_t))
\end{aligned}
\end{equation}
$\overline{\text{bel}}(\mathbf{x}_{t}) $ 식이 한결 간결해졌지만 아직 정확한 $\mathbf{L}_t(\mathbf{x}_t)$ 수식의 유도가 필요하다. $\mathbf{L}_t(\mathbf{x}_t)$는 다음과 같이 전체 $\mathbf{L}_t$에서 분해된 값을 빼줌으로써 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{L}_t(\mathbf{x}_t) & = {\color{Red} \mathbf{L}_t }- {\color{Cyan} \mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) } \\
& = {\color{Red} \frac{1}{2}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1}-\mathbf{B}_t\mathbf{u}_t)^{\intercal} \mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{F}_t\mathbf{x}_{t-1}-\mathbf{B}_t\mathbf{u}_t) } \\
& \quad{\color{Red} + \frac{1}{2}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1})^{\intercal} \mathbf{P}_{t-1}^{-1}(\mathbf{x}_{t-1} - \hat{\mathbf{x}}_{t-1}) } \\
& \quad - {\color{Cyan} \frac{1}{2}(\mathbf{x}_{t-1} - \Psi_t[ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} ])^{\intercal} \Psi^{-1} } \\
& \quad {\color{Cyan} (\mathbf{x}_{t-1} - \Psi_t[ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} ]) }
\end{aligned}
\end{equation}
$\mathbf{L}_t(\mathbf{x}_t)$의 정확한 수식을 얻기 위해 식을 전개하면 다음과 같다. 이 때 $\Psi = (\mathbf{F}^{\intercal}_t\mathbf{R}_t^{-1} \mathbf{F}_t+ \mathbf{P}_{t-1}^{-1})^{-1}$을 적용하여 치환했던 기호를 복원하였다.
\begin{equation}
\begin{aligned}
\mathbf{L}_t(\mathbf{x}_t) & = \mathbf{L}_t - \mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) \\
& = \underline{\underline{\frac{1}{2}\mathbf{x}_{t-1}^{\intercal}\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t\mathbf{x}_{t-1} }} - \underline{ \mathbf{x}_{t-1}^{\intercal}\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) } \\
& \quad + \frac{1}{2}(\mathbf{x}_t - \mathbf{B}_t\mathbf{u}_t)^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) \\
& \quad + \underline{\underline{ \frac{1}{2} \mathbf{x}_{t-1}^{\intercal}\mathbf{P}_{t-1}^{-1}\mathbf{x}_{t-1} }} - \underline{ \mathbf{x}_{t-1}^{\intercal} \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} } + \frac{1}{2}\hat{\mathbf{x}}_{t-1}^{\intercal} \mathbf{P}_{t-1}^{-1} \hat{\mathbf{x}}_{t-1} \\
& \quad - \underline{\underline{ \frac{1}{2}\mathbf{x}_{t-1}^{\intercal} (\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})\mathbf{x}_{t-1} }} \\
& \quad + \underline{ \mathbf{x}_{t-1}^{\intercal}[\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}] } \\
& \quad -\frac{1}{2} [ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}]^{\intercal} (\mathbf{F}_t^{\intercal} \mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1} \\
& \quad [ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}]
\end{aligned}
\end{equation}
- $\underline{\underline{(\cdot)}}$ : $\mathbf{x}_{t-1}$의 2차식
- ${\underline{(\cdot)}}$ : $\mathbf{x}_{t-1}$의 1차식
위 식을 자세히 살펴보면 $\mathbf{x}_{t-1}$ 관련 2차식과 1차식이 서로 소거되어 제거되는 것을 알 수 있다. 이는 $\mathbf{L}_t$에서 $\mathbf{x}_{t-1}$ 성분만을 추출한 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$를 제외해줬으므로 당연한 결과라고 할 수 있다. 소거된 항을 제거하면 $\mathbf{L}_t(\mathbf{x}_t)$을 얻을 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{L}_t(\mathbf{x}_t) & = \frac{1}{2}(\mathbf{x}_t - \mathbf{B}_t\mathbf{u}_t)^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \frac{1}{2}\hat{\mathbf{x}}_{t-1}^{\intercal} \mathbf{P}_{t-1}^{-1} \hat{\mathbf{x}}_{t-1} \\
& \quad - \frac{1}{2} [ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}]^{\intercal} (\mathbf{F}_t^{\intercal} \mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1} \\
& \quad [ \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}]
\end{aligned} }
\end{equation}
$\overline{\text{bel}}(\mathbf{x}_{t})$는 정규분포를 따르기 때문에 $\mathbf{L}_t(\mathbf{x}_t)$ 또한 정규분포를 가지는 2차식 형태(quadratic)으로 나타낼 수 있다. 이전에 수행했던 $\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)$와 마찬가지로 $\mathbf{L}_t(\mathbf{x}_t)$를 편미분하여 평균과 공분산을 구한다.
우선 1차 편미분을 통해 $\mathbf{x}_t$에 대한 평균을 구한다. 이 때, matrix inversion lemma를 사용하여 식을 간결하게 변형시킨다.
\begin{equation}
\begin{aligned}
\frac{\partial \mathbf{L}_t(\mathbf{x}_t)}{\partial \mathbf{x}_t} & = \mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) - \mathbf{R}_t^{-1}\mathbf{F}_t(\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1} [\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}(\mathbf{x}_t - \mathbf{B}_t\mathbf{u}_t) + \mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}] \\
& = {\color{Cyan} [\mathbf{R}_t^{-1} - \mathbf{R}_t^{-1}\mathbf{F}_t(\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1} \mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}] } (\mathbf{x}_t - \mathbf{B}_t\mathbf{u}_t) - \mathbf{R}_t^{-1}\mathbf{F}_t(\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1}\mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1} \\
& = {\color{Cyan} (\mathbf{R}_t + \mathbf{F}_t\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal})^{-1} } (\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) - \mathbf{R}_t^{-1}\mathbf{F}_t(\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1}\mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}
\end{aligned}
\end{equation}
$\frac{\partial \mathbf{L}_t(\mathbf{x}_t)}{\partial \mathbf{x}_t}=0$으로 설정하여 평균을 구한다.
\begin{equation}
\begin{aligned}
{\color{Cyan} (\mathbf{R}_t + \mathbf{F}_t\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal})^{-1} }(\mathbf{x}_t - \mathbf{B}_t \mathbf{u}_t) = \mathbf{R}_t^{-1}\mathbf{F}_t(\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1}\mathbf{P}_{t-1}^{-1}\hat{\mathbf{x}}_{t-1}
\end{aligned}
\end{equation}
위 식을 $\mathbf{x}_t$에 대하여 풀면 다음과 같은 간단한 식이 도출된다.
\begin{equation}
\begin{aligned}
\mathbf{x}_t & = \mathbf{B}_t \mathbf{u}_t + \underbrace{ (\mathbf{R}_t + \mathbf{F}_t\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal}) \mathbf{R}_t^{-1}\mathbf{F}_t }_{\mathbf{F}_t + \mathbf{F}_t\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t} \underbrace{ (\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{P}_{t-1}^{-1})^{-1} \mathbf{P}_{t-1}^{-1}}_{(\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{I})^{-1}} \hat{\mathbf{x}}_{t-1} \\
& = \mathbf{B}_t \mathbf{u}_t + \mathbf{F}_t \underbrace{ (\mathbf{I} + \mathbf{P}_{t-1}\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t)(\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal}\mathbf{R}_t^{-1}\mathbf{F}_t + \mathbf{I})^{-1}}_{\mathbf{I}} \hat{\mathbf{x}}_{t-1} \\
& = {\color{Mahogany} \mathbf{B}_t \mathbf{u}_t + \mathbf{F}_t \hat{\mathbf{x}}_{t-1} }
\end{aligned}
\end{equation}
다음으로 2차 편미분을 통해 공분산의 역행렬을 구할 수 있다.
\begin{equation}
\begin{aligned}
\frac{\partial^2 \mathbf{L}_t(\mathbf{x}_t)}{\partial \mathbf{x}^2_t} & = {\color{Mahogany} (\mathbf{R}_t + \mathbf{F}_t\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal})^{-1} }
\end{aligned}
\end{equation}
최종적으로 $\overline{\text{bel}}(\mathbf{x}_{t})$는 다음과 같이 정리할 수 있다.
\begin{equation}
\begin{aligned}
\underbrace{\overline{\text{bel}}(\mathbf{x}_{t})}_{\sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1}) } & = \int \underbrace{p(\mathbf{x}_{t} \ | \ \mathbf{x}_{t-1}, \mathbf{u}_{t})}_{\sim \mathcal{N}(\mathbf{F}_t\mathbf{x}_{t-1}+\mathbf{B}_t \mathbf{u}_t), \mathbf{R}_{t}} \underbrace{\text{bel}(\mathbf{x}_{t-1})}_{\quad \sim \mathcal{N}(\hat{\mathbf{x}}_{t-1}, \mathbf{P}_{t-1})} d \mathbf{x}_{t-1} \\
& = \eta \int \exp(-\mathbf{L}_{t}) d \mathbf{x}_{t-1} \\
& = \eta \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t) - \mathbf{L}_t(\mathbf{x}_t)) d \mathbf{x}_{t-1} \\
& = \eta \exp(-\mathbf{L}_t(\mathbf{x}_t)) \int \exp(-\mathbf{L}_t(\mathbf{x}_{t-1}, \mathbf{x}_t)) d \mathbf{x}_{t-1} \\
& = \eta' \exp(-\mathbf{L}_t(\mathbf{x}_t))
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
& \text{mean } : \hat{\mathbf{x}}_{t|t-1} = {\color{Mahogany} \mathbf{F}_t\hat{\mathbf{x}}_{t-1|t-1}+\mathbf{B}_t \mathbf{u}_t }\\
& \text{covariance }: \mathbf{P}_{t|t-1} = {\color{Mahogany} \mathbf{F}_t\mathbf{P}_{t-1}\mathbf{F}_t^{\intercal} + \mathbf{R}_t }
\end{aligned} }
\end{equation}
위 식은 prediction 스텝의 평균과 공분산을 구하는데 사용된다.
Derivation of KF update step (ver. 1)
다음으로 ${\text{bel}}(\mathbf{x}_{t})$ 수식을 유도해보자. ${\text{bel}}(\mathbf{x}_{t})$에서 구하고자 하는 평균과 분산은 다음과 같다.
\begin{equation}
\begin{aligned}
& \underbrace{{\text{bel}}(\mathbf{x}_{t})}_{\sim \mathcal{N}(\hat{\mathbf{x}}_{t|t}, \mathbf{P}_{t|t}) } = \eta \underbrace{p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t})}_{\sim \mathcal{N}(\mathbf{H}_t\mathbf{x}_{t}, \mathbf{Q}_{t})} \underbrace{\overline{\text{bel}(\mathbf{x}}_{t})}_{\quad \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1})} \end{aligned}
\end{equation}
위 식을 가우시안 형태로 펼쳐보면 다음과 같다.
\begin{equation}
\begin{aligned}
& {\text{bel}}(\mathbf{x}_{t}) = \eta \exp \Big(-\frac{1}{2}(\mathbf{z}_t - \mathbf{H}_t\mathbf{x}_{t})^{\intercal} \mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t\mathbf{x}_{t}) \Big) \cdot \exp \Big( -\frac{1}{2}(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})^{\intercal} {\mathbf{P}}_{t|t-1}^{-1}(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1}) \Big) \end{aligned}
\end{equation}
위 식은 다음과 같이 더 간단하게 치환할 수 있다.
\begin{equation}
\begin{aligned}
& {\text{bel}}(\mathbf{x}_{t}) = \eta \exp(-{\color{Mahogany} \mathbf{J}_{t} })
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
\text{where, } {\color{Mahogany} \mathbf{J}_t } = \frac{1}{2}(\mathbf{z}_t - \mathbf{H}_t\mathbf{x}_{t})^{\intercal} \mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t\mathbf{x}_{t}) + \frac{1}{2}(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})^{\intercal} {\mathbf{P}}_{t|t-1}^{-1}(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})
\end{aligned} }
\end{equation}
${\text{bel}}(\mathbf{x}_{t})$는 가우시안 분포를 따르므로 $\mathbf{J}_t$를 편미분하여 평균과 공분산을 구할 수 있다.
\begin{equation}
\begin{aligned}
\frac{\partial \mathbf{J}_t}{\partial \mathbf{x}_t}
= -\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t\mathbf{x}_{t}) + \mathbf{P}_{t|t-1}^{-1}(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\frac{\partial^2 \mathbf{J}_t}{\partial \mathbf{x}^2_t}
= \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t + \mathbf{P}_{t|t-1}^{-1} := \mathbf{P}_{t|t}^{-1} \quad \cdots {\color{Mahogany} \text{covariance}^{-1} }
\end{aligned}
\end{equation}
1차 편미분 $\frac{\partial \mathbf{J}_t}{\partial \mathbf{x}_{t}}$를 0으로 설정하면 다음과 같은 공식을 얻을 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t {\color{Red} \mathbf{x}_{t} }) = \mathbf{P}_{t|t-1}^{-1}({\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1})
\end{aligned}
\end{equation}
위 식을 ${\color{Red} \mathbf{x}_{t} }$에 대해 풀면 다음과 같다.
\begin{equation} \label{eq:derivkf5}
\begin{aligned}
& \Leftrightarrow \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t {\color{Red} \mathbf{x}_{t} } + \mathbf{H}_t\hat{\mathbf{x}}_{t|t-1} - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) = \mathbf{P}_{t|t-1}^{-1}({\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1}) \\
& \Leftrightarrow \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) - \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t({\color{Red}\mathbf{x}_t } - \hat{\mathbf{x}}_{t|t-1}) = \mathbf{P}_{t|t-1}^{-1}({\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1}) \\
& \Leftrightarrow \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) = (\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t + \mathbf{P}_{t|t-1}^{-1})({\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1}) \\
& \Leftrightarrow \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}(\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) = \mathbf{P}_{t|t}^{-1}({\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1}) \\
& \Leftrightarrow \underline{ \mathbf{P}_{t|t}\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1} } (\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) = {\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1} \\
& \Leftrightarrow \underline{ \mathbf{K}_t } (\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) = {\color{Red}\mathbf{x}_{t} } - \hat{\mathbf{x}}_{t|t-1} \\
& \therefore {\color{Red}\mathbf{x}_{t} } = \hat{\mathbf{x}}_{t|t-1} + \mathbf{K}_t(\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) \quad \cdots {\color{Mahogany} \text{mean} }
\end{aligned}
\end{equation}
따라서 $\text{bel}(\mathbf{x}_{t})$의 평균과 분산은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
& \text{kalman gain }: \mathbf{K}_t = \mathbf{P}_{t|t} \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1} \\
& \text{mean }: \hat{\mathbf{x}}_{t|t} = \hat{\mathbf{x}}_{t|t-1} + \mathbf{K}_t(\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) \\
& \text{covariance }: \mathbf{P}_{t|t} = (\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t + \mathbf{P}_{t|t-1}^{-1})^{-1}
\end{aligned} }
\end{equation}
하지만 $\text{bel}(\mathbf{x}_{t})$의 분산 $\mathbf{P}_{t|t}$을 계산할 때 역행렬을 계산해야 하므로 시간이 오래 걸리는 단점이 존재한다. Matrix inversion lemma를 사용하여 해당 수식을 변형할 수 있다.
\begin{equation} \label{eq:derivkf6}
\begin{aligned}
\mathbf{P}_{t|t} & = (\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t + \mathbf{P}_{t|t-1}^{-1})^{-1} \\
& = (\mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t)^{-1} \\
& = \mathbf{P}_{t|t-1} - \underline{\underline{ \mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal}(\mathbf{Q}_t + \mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal})^{-1} }} \mathbf{H}_t \mathbf{P}_{t|t-1} \\
& = \mathbf{P}_{t|t-1} - \underline{\underline{ \mathbf{K}_t }} \mathbf{H}_t \mathbf{P}_{t|t-1} \\
& = (\mathbf{I} - \mathbf{K}_t\mathbf{H}_t) \mathbf{P}_{t|t-1}
\end{aligned}
\end{equation}
(\ref{eq:derivkf5})와 (\ref{eq:derivkf6})의 칼만 게인 $\mathbf{K}_t$ 사이에는 다음과 같이 변형이 존재한다.
\begin{equation}
\begin{aligned}
\mathbf{K}_t & = \underline{ \mathbf{P}_{t|t} \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1} } \\
& = \mathbf{P}_{t|t} \mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1} \underbrace{(\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)(\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1}}_{\mathbf{I}} \\
& = \mathbf{P}_{t|t}(\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t \mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{H}_t^{\intercal} \underbrace{\mathbf{Q}_t^{-1}\mathbf{Q}_t}_{\mathbf{I}})(\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1} \\
& = \mathbf{P}_{t|t}(\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t \mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{H}_t^{\intercal}) (\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1} \\
& = \mathbf{P}_{t|t}(\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t \mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \underbrace{\mathbf{P}_{t|t-1}^{-1}\mathbf{P}_{t|t-1}}_{\mathbf{I}} \mathbf{H}_t^{\intercal} )(\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1} \\
& = \mathbf{P}_{t|t} \underbrace{ (\mathbf{H}_t^{\intercal}\mathbf{Q}_t^{-1}\mathbf{H}_t + \mathbf{P}_{t|t-1}^{-1})}_{\mathbf{P}_{t|t}^{-1}}\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} (\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1} \\
& = \underline{\underline{ \mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} (\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1} }}
\end{aligned}
\end{equation}
최종적으로 ${\text{bel}}(\mathbf{x}_{t})$는 다음과 같이 정리할 수 있다.
\begin{equation}
\begin{aligned}
\underbrace{{\text{bel}}(\mathbf{x}_{t})}_{\sim \mathcal{N}(\hat{\mathbf{x}}_{t|t}, \mathbf{P}_{t|t}) } & = \eta \underbrace{p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t})}_{\sim \mathcal{N}(\mathbf{H}_t\mathbf{x}_{t}, \mathbf{Q}_{t})} \underbrace{\overline{\text{bel}(\mathbf{x}}_{t})}_{\quad \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1})} \\
& = \eta \exp(-\mathbf{J}_{t})
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned}
& \text{kalman gain }: \mathbf{K}_t = \mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} (\mathbf{H}_t\mathbf{P}_{t|t-1}\mathbf{H}_t^{\intercal} + \mathbf{Q}_t)^{-1} \\
& \text{mean }: \hat{\mathbf{x}}_{t|t} = \hat{\mathbf{x}}_{t|t-1} + \mathbf{K}_t(\mathbf{z}_t - \mathbf{H}_t \hat{\mathbf{x}}_{t|t-1}) \\
& \text{covariance }: \mathbf{P}_{t|t} = (\mathbf{I} - \mathbf{K}_{t}\mathbf{H}_{t})\mathbf{P}_{t|t-1}
\end{aligned} }
\end{equation}
Derivation of KF update step (ver. 2)
${\text{bel}}(\mathbf{x}_{t})$는 likelihood와 prior의 곱으로 이루어져 있기 때문에 조건부 확률(conditional pdf)을 구함으로써 posterior의 평균과 분산을 비교적 간단하게 구할 수 있다.
\begin{equation}
\begin{aligned}
\underbrace{{\text{bel}}(\mathbf{x}_{t})}_{\sim \mathcal{N}(\hat{\mathbf{x}}_{t|t}, \mathbf{P}_{t|t}) } & = \eta \underbrace{p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t})}_{\sim \mathcal{N}(\mathbf{H}_t\mathbf{x}_{t}, \mathbf{Q}_{t})} \underbrace{\overline{\text{bel}(\mathbf{x}}_{t})}_{\quad \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1})} \\
\text{posterior} & = \text{ likelihood } \times \text{ prior }
\end{aligned}
\end{equation}
Conditional gaussian distribution
두 벡터 확률변수 $\mathbf{x}, \mathbf{z}$가 주어졌을 때 조건부 확률분포 $p(\mathbf{x}|\mathbf{z})$가 가우시안 분포를 따른다고 하면
\begin{equation}
\begin{aligned}
p(\mathbf{x}| \mathbf{z}) & = \frac{p(\mathbf{x},\mathbf{z})}{p(\mathbf{z})} \\ & = \frac{p(\mathbf{z} | \mathbf{x})p(\mathbf{x})}{p(\mathbf{z})} \\& = \eta \cdot p(\mathbf{z}|\mathbf{x})p(\mathbf{x}) \\
& \sim \mathcal{N}(\mathbb{E}(\mathbf{x}|\mathbf{z}), \mathbf{C}_{x|z})
\end{aligned}
\end{equation}
가 된다. 평균 $\mathbb{E}(\mathbf{x}|\mathbf{z})$과 분산 $\mathbf{C}_{x|z}$은 아래와 같다.
\begin{equation}
\boxed{ \begin{aligned}
& \mathbb{E}(\mathbf{x}|\mathbf{z})= \mathbb{E}(\mathbf{x}) + \mathbf{C}_{xz}\mathbf{C}_{zz}^{-1}(\mathbf{z} - \mathbb{E}(\mathbf{z})) \\
& \mathbf{C}_{x|z} = \mathbf{C}_{xx} - \mathbf{C}_{xz}\mathbf{C}_{zz}^{-1}\mathbf{C}_{xz}^{\intercal}
\end{aligned} }
\end{equation}
그림으로 설명하면 다음과 같다
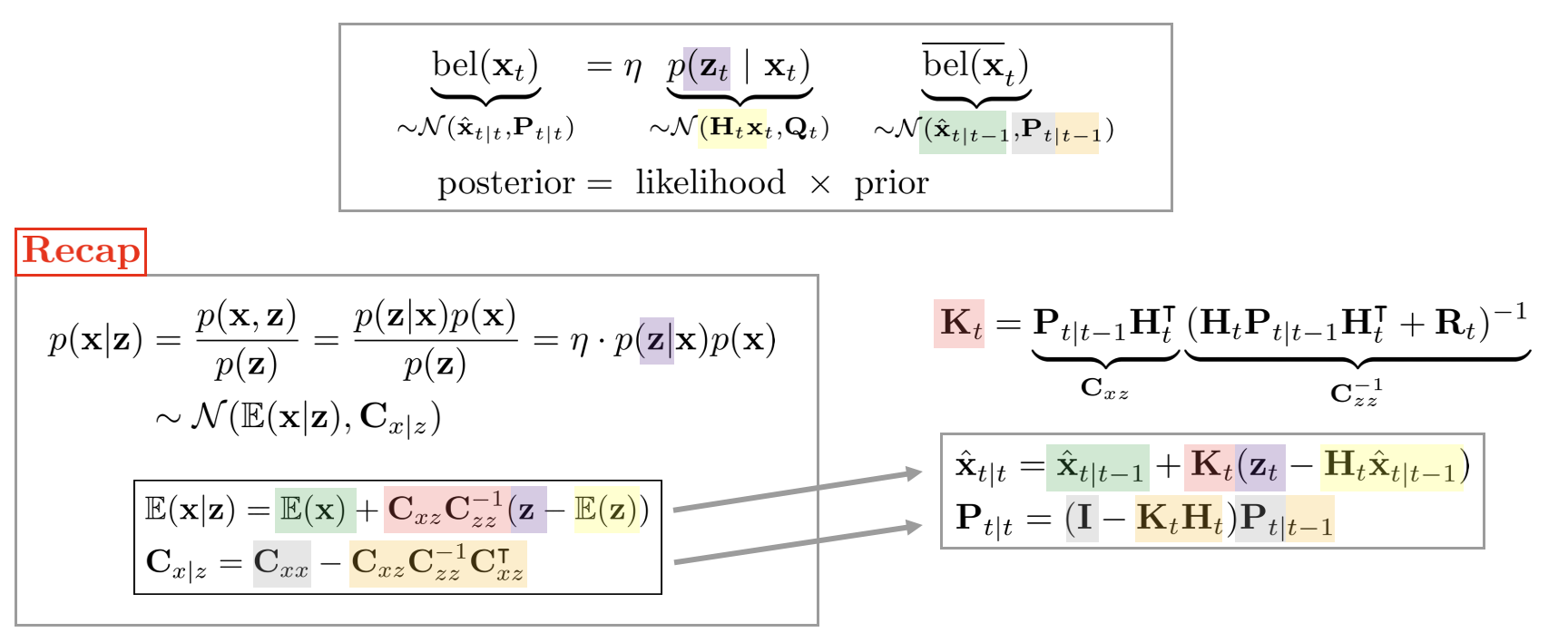
MAP, GN, and EKF relationship
Traditional EKF derivation
EKF의 관측 모델 함수가 다음과 같이 주어졌다고 하자. 전개의 편의를 위해 관측 노이즈 $\mathbf{v}_{t}$를 밖으로 위치하였다.
\begin{equation}
\begin{aligned}
& \text{Observation Model: } & \mathbf{z}_{t} = \mathbf{h}(\mathbf{x}_{t}) + \mathbf{v}_{t}
\end{aligned}
\end{equation}
EKF의 correction 스텝은 아래 수식을 전개하여 평균 $\hat{\mathbf{x}}_{t|t}$와 공분산 $\mathbf{P}_{t|t}$를 유도한다.
\begin{equation}
\begin{aligned}
\text{bel}( \mathbf{x}_{t}) = \eta \cdot p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t}) \overline{\text{bel}}( \mathbf{x}_{t}) \sim \mathcal{N}(\hat{\mathbf{x}}_{t|t}, \mathbf{P}_{t|t})
\end{aligned}
\end{equation}
- $p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t}) \sim \mathcal{N}( \mathbf{h}_{t}(\mathbf{x}_{t}) , \mathbf{R}_{t})$
- $\overline{\text{bel}}( \mathbf{x}_{t}) \sim \mathcal{N}( \hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1})$
\begin{equation}
\boxed{ \begin{aligned}
& \hat{\mathbf{x}}_{t|t} = \mathbf{K}_{t} ( \mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t-1})) \\
& \mathbf{P}_{t|t} = (\mathbf{I} - \mathbf{K}_{t}\mathbf{H}_{t})\mathbf{P}_{t|t-1}
\end{aligned} }
\end{equation}
MAP-based EKF derivation
Start from MAP estimator
Correction 스텝을 유도하는 방법으로 posterior의 확률을 최대화하는 maximum a posteriori(MAP) 추정을 사용할 수 있다. 자세한 내용은 [12]를 참고하여 작성하였다.
\begin{equation} \label{eq:map1}
\begin{aligned}
\hat{\mathbf{x}}_{t|t} & = \arg\max_{ \mathbf{x}_{t}} \text{bel}(\mathbf{x}_{t}) \\
& = \arg\max_{ \mathbf{x}_{t}} p(\mathbf{x}_{t} | \mathbf{z}_{1:t}, \mathbf{u}_{1:t}) \quad \cdots \text{posterior} \\
& \propto \arg\max_{ \mathbf{x}_{t}} p(\mathbf{z}_{t} | \mathbf{x}_{t}) \overline{\text{bel}}(\mathbf{x}_{t}) \quad \cdots \text{likelihood} \cdot \text{prior} \\
& \propto \arg\max_{\mathbf{x}_{t}} \exp \bigg( -\frac{1}{2} \bigg[ (\mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t}))^{\intercal} \mathbf{R}_{t}^{-1} (\mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t})) \\
& \quad\quad\quad \quad \quad \quad + ( \mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})^{\intercal} \mathbf{P}_{t|t-1}^{-1} ( \mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1}) \bigg] \bigg)
\end{aligned}
\end{equation}
- $p(\mathbf{z}_{t} \ | \ \mathbf{x}_{t}) \sim \mathcal{N}( \mathbf{h}_{t}(\mathbf{x}_{t}) , \mathbf{R}_{t})$
- $\overline{\text{bel}}( \mathbf{x}_{t}) \sim \mathcal{N}( \hat{\mathbf{x}}_{t|t-1}, \mathbf{P}_{t|t-1})$
마이너스 부호를 제거하면 최대화(maximization) 문제가 최소화(minimization) 문제로 변하고 다음과 같은 최적화 식으로 정리할 수 있다.
\begin{equation} \label{eq:map2}
\begin{aligned}
\hat{\mathbf{x}}_{t|t} & \propto \arg\min_{\mathbf{x}_{t}} \exp \bigg( (\mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t}))^{\intercal} \mathbf{R}_{t}^{-1} (\mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t})) \\
& \quad\quad\quad\quad\quad\quad + ( \mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1} )^{\intercal} \mathbf{P}^{-1}_{t|t-1} ( \mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1} ) \bigg) \end{aligned}
\end{equation}
\begin{equation} \label{eq:map3}
\boxed{ \begin{aligned}
\hat{\mathbf{x}}_{t|t} & = \arg\min_{\mathbf{x}_{t}} \left\| \mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t}) \right\|_{\mathbf{R}_{t}^{-1}} + \left\| \mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1} \right\|_{\mathbf{P}_{t|t-1}^{-1}}
\end{aligned} }
\end{equation}
- $\left\| \mathbf{a} \right\|_{\mathbf{B}} = \mathbf{a}^{\intercal}\mathbf{B}\mathbf{a}$
(\ref{eq:map3}) 내부의 식을 전개하고 cost function $\mathbf{C}_{t}$라고 정의하면 다음과 같다. 이 때, $\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1}$의 순서를 바꿔도 전체 값에는 영향을 주지 않는다.
\begin{equation}
\begin{aligned}
\mathbf{C}_{t} = (\mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t}))^{\intercal} \mathbf{R}_{t}^{-1} (\mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t})) + ( \hat{\mathbf{x}}_{t|t-1} - \mathbf{x}_{t} )^{\intercal} \mathbf{P}^{-1}_{t|t-1} ( \hat{\mathbf{x}}_{t|t-1} - \mathbf{x}_{t} )
\end{aligned}
\end{equation}
이를 행렬 형태로 표현하면 다음과 같다.
\begin{equation} \label{eq:map4}
\begin{aligned}
\mathbf{C}_{t} = \begin{bmatrix} \hat{\mathbf{x}}_{t|t-1} - \mathbf{x}_{t} \\ \mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t})\end{bmatrix}^{\intercal} \begin{bmatrix} \mathbf{P}^{-1}_{t|t-1} & \mathbf{0} \\ \mathbf{0} & \mathbf{R}^{-1}_{t} \end{bmatrix} \begin{bmatrix} \hat{\mathbf{x}}_{t|t-1} - \mathbf{x}_{t} \\ \mathbf{z}_{t} - \mathbf{h}(\mathbf{x}_{t})\end{bmatrix}
\end{aligned}
\end{equation}
MLE of new observation function
위 식을 만족하는 새로운 관측 함수를 다음과 같이 정의할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{y}_{t} & = \mathbf{g}(\mathbf{x}_{t}) + \mathbf{e}_{t} \\
& \sim \mathcal{N}(\mathbf{g}(\mathbf{x}_{t}), \mathbf{P}_{\mathbf{e}})
\end{aligned} }
\end{equation}
- $\mathbf{y}_{t} = \begin{bmatrix} \hat{\mathbf{x}}_{t|t-1} \\ \mathbf{z}_{t} \end{bmatrix}$
- $\mathbf{g}(\mathbf{x}_{t}) = \begin{bmatrix} \mathbf{x}_{t} \\ \mathbf{h}(\mathbf{x}_{t}) \end{bmatrix}$
- $\mathbf{e}_{t} \sim \mathcal{N}(0, \mathbf{P}_{\mathbf{e}})$
- $\mathbf{P}_{\mathbf{e}} = \begin{bmatrix} \mathbf{P}_{t|t-1} & \mathbf{0} \\ \mathbf{0} & \mathbf{R}_{t} \end{bmatrix}$
비선형 함수 $\mathbf{g}(\mathbf{x}_{t})$는 다음과 같이 선형화할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{g}(\mathbf{x}_{t}) & \approx \mathbf{g}(\hat{\mathbf{x}}_{t|t-1}) + \mathbf{J}_{t}(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1}) \\
& = \mathbf{g}(\hat{\mathbf{x}}_{t|t-1}) + \mathbf{J}_{t}\delta \hat{\mathbf{x}}_{t|t-1}
\end{aligned}
\end{equation}
자코비안 $\mathbf{J}_{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{J}_{t} & = \frac{\partial \mathbf{g}}{\partial \mathbf{x}_{t}}\bigg|_{\mathbf{x}_{t} = \hat{\mathbf{x}}_{t|t-1}} \\
& \frac{\partial \begin{bmatrix} \mathbf{x}_{t} \\ \mathbf{h}(\mathbf{x}_{t}) \end{bmatrix} }{\partial \mathbf{x}_{t}}\bigg|_{\mathbf{x}_{t} = \hat{\mathbf{x}}_{t|t-1}} \\
& \frac{\partial \begin{bmatrix} \mathbf{x}_{t} \\ \mathbf{h}(\hat{\mathbf{x}}_{t|t-1}) + \mathbf{H}_{t} (\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1}) \end{bmatrix} }{\partial \mathbf{x}_{t}}\bigg|_{\mathbf{x}_{t} = \hat{\mathbf{x}}_{t|t-1}} \\
& = \begin{bmatrix} \mathbf{I} \\ \mathbf{H}_{t} \end{bmatrix}
\end{aligned}
\end{equation}
따라서 다음과 같이 $\mathbf{y}_{t}$에 대한 likelihood를 전개할 수 있다.
\begin{equation} \label{eq:map5}
\begin{aligned}
p(\mathbf{y}_{t} | \mathbf{x}_{t}) & \sim \mathcal{N}(\mathbf{g}(\mathbf{x}_{t}), \mathbf{P}_{\mathbf{e}}) \\
& = \eta \cdot \exp\bigg( -\frac{1}{2}(\mathbf{y}_{t} - \mathbf{g}(\mathbf{x}_{t}))^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1}(\mathbf{y}_{t} - \mathbf{g}(\mathbf{x}_{t})) \bigg)
\end{aligned}
\end{equation}
즉, 기존의 $\text{bel}(\mathbf{x}_{t})$에 대한 maximum a posteriori(MAP) 문제는 $p(\mathbf{y}_{t} | \mathbf{x}_{t})$에 대한 maximum likelihood estimation(MLE) 문제를 푸는 것으로 귀결된다. (\ref{eq:map5}) 식을 MLE로 풀면 다음과 같다.
\begin{equation} \label{eq:map6}
\begin{aligned}
\hat{\mathbf{x}}_{t|t} & = \arg\max_{\mathbf{x}_{t}} p(\mathbf{y}_{t} | \mathbf{x}_{t}) \\
& \propto \arg\min_{\mathbf{x}_{t}} -\ln p(\mathbf{y}_{t} | \mathbf{x}_{t}) \\
& \propto \arg\min_{\mathbf{x}_{t}} \frac{1}{2} (\mathbf{y}_{t} - \mathbf{g}(\mathbf{x}_{t}))^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1}(\mathbf{y}_{t} - \mathbf{g}(\mathbf{x}_{t})) \\
& \propto \arg\min_{\mathbf{x}_{t}} \left\| \mathbf{y}_{t} - \mathbf{g}(\mathbf{x}_{t}) \right\|_{\mathbf{P}_{\mathbf{e}}^{-1}}
\end{aligned}
\end{equation}
Gauss-Newton Optimization
(\ref{eq:map6}) 식은 최소제곱법의 형태를 지닌다. 특히 가중치 $\mathbf{P}_{\mathbf{e}}^{-1}$가 중간에 곱해지므로 weighted least squares(WLS)라고도 부른다. 식을 선형화한 후 다시 정리하면 아래와 같다.
\begin{equation}
\begin{aligned}
\hat{\mathbf{x}}_{t|t} & = \arg\min_{\mathbf{x}_{t}} \left\| \mathbf{y}_{t} - \mathbf{g}(\mathbf{x}_{t}) \right\|_{\mathbf{P}_{\mathbf{e}}^{-1}} \\
& = \arg\min_{\mathbf{x}_{t}} \left\| \mathbf{y}_{t} - \mathbf{g}(\hat{\mathbf{x}}_{t|t-1}) - \mathbf{J}_{t} \delta \hat{\mathbf{x}}_{t|t-1} \right\|_{\mathbf{P}_{\mathbf{e}}^{-1}} \\
& = \arg\min_{\mathbf{x}_{t}} \left\| \mathbf{J}_{t} \delta \hat{\mathbf{x}}_{t|t-1} - (\mathbf{y}_{t} - \mathbf{g}(\hat{\mathbf{x}}_{t|t-1}) ) \right\|_{\mathbf{P}_{\mathbf{e}}^{-1}} \\
& = \arg\min_{\mathbf{x}_{t}} \left\| \mathbf{J}_{t} \delta \hat{\mathbf{x}}_{t|t-1} - \mathbf{r}_{t} \right\|_{\mathbf{P}_{\mathbf{e}}^{-1}} \\
\end{aligned}
\end{equation}
- $\delta \hat{\mathbf{x}}_{t|t-1} = \mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1}$ : 표현의 편의를 위해 $\mathbf{x}_{t}$를 true 상태로 표현
선형화된 residual term $\mathbf{r}_{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{r}_{t} & = \mathbf{y}_{t} - \mathbf{g}(\hat{\mathbf{x}}_{t|t-1}) \\
& = \mathbf{J}_{t} \delta \hat{\mathbf{x}}_{t|t-1} + \mathbf{e} \\ & \sim \mathcal{N}(0, \mathbf{P}_{\mathbf{e}})
\end{aligned}
\end{equation}
GN의 정규방정식으로 통해 해를 구하면 다음과 같다.
\begin{equation}
\begin{aligned}
& (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t}) \delta \hat{\mathbf{x}}_{t|t-1} = \mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{r}_{t} \\
\end{aligned}
\end{equation}
\begin{equation}
\boxed{ \begin{aligned} & \therefore \delta \hat{\mathbf{x}}_{t|t-1} = (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1}\mathbf{J}_{t})^{-1} \mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{r}_{t}
\end{aligned} }
\end{equation}
위 식에서 $(\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t})$ 부분을 일반적으로 근사 헤시안(approximate hessian) 행렬 $\tilde{\mathbf{H}}$이라고 부른다.
Posterior covariance matrix $\mathbf{P}_{t|t}$
$\mathbf{P}_{t|t}$는 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{P}_{t|t}
=& \mathbb{E}[(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})(\mathbf{x}_{t} - \hat{\mathbf{x}}_{t|t-1})^{\intercal}] \\
=& \mathbb{E}(\delta \hat{\mathbf{x}}_{t|t-1}\delta \hat{\mathbf{x}}_{t|t-1}^{\intercal}) \\
=& \mathbb{E}\bigg[
(\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t})^{-1} \mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{r}_{t}
\mathbf{r}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-\intercal} \mathbf{J}_{t} (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t})^{-\intercal} \bigg] \\
=&
(\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t})^{-1} \mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbb{E}(\mathbf{r}_{t}
\mathbf{r}_{t}^{\intercal}) \mathbf{P}_{\mathbf{e}}^{-\intercal} \mathbf{J}_{t} (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t})^{-\intercal} \quad {\color{Mahogany}\leftarrow \mathbb{E}(\mathbf{r}_{t}\mathbf{r}_{t}^{\intercal}) = \mathbf{P}_{\mathbf{e}} } \\
=& \left(
{\color{Mahogany}{\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t}}}
\right)^{-1} \\
=& \left(
\begin{bmatrix} \mathbf{I} & \mathbf{H}_{t}^{\intercal} \end{bmatrix}
\begin{bmatrix} \mathbf{P}_{t|t-1} & \mathbf{0} \\ \mathbf{0} & \mathbf{R}_{t} \end{bmatrix}^{-1}
\begin{bmatrix} \mathbf{I} \\ \mathbf{H}_{t} \end{bmatrix}
\right)^{-1} \\
=& \left( \mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1}\mathbf{H}_{t} \right)^{-1} \\
=& \mathbf{P}_{t|t-1} - \mathbf{P}_{t|t-1}\mathbf{H}_{t}^{\intercal} (\mathbf{H}_{t}\mathbf{P}_{t|t-1}\mathbf{H}_{t}^{\intercal} + \mathbf{R}_{t})^{-1} \mathbf{H}_{t} \mathbf{P}_{t|t-1} \quad {\color{Mahogany} \leftarrow \text{matrix inversion lemmas} } \\
=& {\color{Mahogany}{(\mathbf{I} - \mathbf{K}_{t}\mathbf{H}_{t}) \mathbf{P}_{t|t-1}}}
\end{aligned} }
\end{equation}
위 식의 다섯번 째 줄에서 보다시피 GN을 통해 구한 근사 헤시안 행렬의 역함수 $\tilde{\mathbf{H}}^{-1}$와 EKF의 posterior 공분산 $\mathbf{P}_{t|t}$는 같은 값을 가지는 것을 알 수 있다.
\begin{equation}
\begin{aligned}
\tilde{\mathbf{H}}^{-1} = (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{\mathbf{e}}^{-1} \mathbf{J}_{t})^{-1} = \mathbf{P}_{t|t}
\end{aligned}
\end{equation}
Posterior mean $\mathbf{x}_{t|t}$
GN을 반복적으로 수행함에 따라 $j$번째 $\mathbf{x}_{t|t, j}$는 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\hat{\mathbf{x}}_{t|t,j+1}
=& \hat{\mathbf{x}}_{t|t,j} + \delta \hat{\mathbf{x}}_{t|t,j} \\
=& \hat{\mathbf{x}}_{t|t,j} + (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{t|t-1}^{-1} \mathbf{J}_{t})^{-1} (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{t|t-1}^{-1} \mathbf{r}_{t}) \\
=& (\mathbf{J}_{t}^{\intercal} \mathbf{P}_{t|t-1}^{-1} \mathbf{J}_{t})^{-1} \mathbf{J}_{t}^{\intercal} \mathbf{P}_{t|t-1}^{-1} (\mathbf{y}_{t} - \mathbf{g}(\hat{\mathbf{x}}_{t|t,j}) + \mathbf{J}_{t} \hat{\mathbf{x}}_{t|t,j}) \quad {\color{Mahogany} \leftarrow \mathbf{r}_{t} = \mathbf{y}_{t} - \mathbf{g}(\hat{\mathbf{x}}_{t|t,j}) }\\
=&
\left( \mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \mathbf{H}_{t} \right)^{-1}
\begin{bmatrix} \mathbf{P}_{t|t-1}^{-1} & \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \end{bmatrix}
\begin{bmatrix}
\hat{\mathbf{x}}_{t|t-1} \\
\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}) + \mathbf{H}_{t} \hat{\mathbf{x}}_{t|t,j}
\end{bmatrix} \quad {\color{Mahogany} \leftarrow \text{expand } \mathbf{J}_{t} } \\
=&
\left( \mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \mathbf{H}_{t} \right)^{-1}
\left(
\mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1}(\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}) + \mathbf{H}_{t} \hat{\mathbf{x}}_{t|t,j}) + \mathbf{P}_{t|t-1}^{-1} \hat{\mathbf{x}}_{t|t-1}
\right) \\
=&
\left( \mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \mathbf{H}_{t} \right)^{-1}
\left(
\mathbf{H}^{\intercal}\mathbf{R}_{t}^{-1}(\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}) - \mathbf{H}_{t}(\hat{\mathbf{x}}_{t|t-1} - \hat{\mathbf{x}}_{t|t,j}) + \mathbf{H}_{t} \hat{\mathbf{x}}_{t|t-1}) + \mathbf{P}_{t|t-1}^{-1} \hat{\mathbf{x}}_{t|t-1}
\right) \\
=&
\left( \mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \mathbf{H}_{t} \right)^{-1}
\left(
\mathbf{H}^{\intercal}\mathbf{R}_{t}^{-1}(\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}) - \mathbf{H}_{t}(\hat{\mathbf{x}}_{t|t-1} - \hat{\mathbf{x}}_{t|t,j})) + \underbrace{(\mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \mathbf{H}_{t} )\hat{\mathbf{x}}_{t|t-1}}_{\hat{\mathbf{x}}_{t|t-1}}
\right) \\
=&
\hat{\mathbf{x}}_{t|t-1} +
{\color{Mahogany}{
\left( \mathbf{P}_{t|t-1}^{-1} + \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1} \mathbf{H}_{t} \right)^{-1} \mathbf{H}_{t}^{\intercal}\mathbf{R}_{t}^{-1}
}}
(\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}) - \mathbf{H}_{t}(\hat{\mathbf{x}}_{t|t-1} - \hat{\mathbf{x}}_{t|t,j})) \\
=&
\hat{\mathbf{x}}_{t|t-1} + {\color{Mahogany}{ \mathbf{K}_{t} }} (\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}) - \mathbf{H}_{t}(\hat{\mathbf{x}}_{t|t-1} - \hat{\mathbf{x}}_{t|t,j}))
\end{aligned} }
\end{equation}
위 식은 IEKF의 (\ref{eq:iekf-cor}) 식과 동일하다. 마지막 식에서 보다시피 Gauss-Newton을 통해 EKF의 해를 추정하는 것과 IEKF를 통해 해를 추정하는 것은 동일한 의미를 지닌다. 만약 처음 iteration $j=0$인 경우 $\hat{\mathbf{x}}_{t|t,0} = \hat{\mathbf{x}}_{t|t-1}$이 되어서 식은 다음과 같이 정리된다.
\begin{equation}
\boxed{ \begin{aligned}
\hat{\mathbf{x}}_{t|t} = \hat{\mathbf{x}}_{t|t-1} + \mathbf{K}_{t} (\mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t-1}))
\end{aligned} }
\end{equation}
이는 EKF의 해와 동일하다. 즉, EKF는 GN iteration=1과 동일한 의미를 지니며 IEKF는 GN과 동일한 연산을 수행하는 것을 알 수 있다.
Derivation of IESKF update step
본 섹션에서는 IESKF 과정 중 업데이트 스텝부터 $\delta \hat{\mathbf{x}}$를 구하는 중간 유도 과정에 대해 설명한다. 이는 주로 링크의 내용을 참고하여 유도하였다. 우선 (\ref{eq:ieskf6}) 업데이트 공식부터 다시 살펴보자
\begin{equation}
\boxed{ \begin{aligned}
\arg\min_{\delta \hat{\mathbf{x}}_{t|t,j}} \quad & \left\| \mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t-1}, 0, 0) - \mathbf{H}_{t} \delta\hat{\mathbf{x}}_{t|t,j} \right\|_{\mathbf{H}_{\mathbf{v}}\mathbf{R}^{-1}\mathbf{H}_{\mathbf{v}}^{\intercal}} + \left\| \hat{\mathbf{x}}_{t|t,j} - \hat{\mathbf{x}}_{t|t-1} + \mathbf{J}_{t,j}\delta\hat{\mathbf{x}}_{t|t,j} \right\|_{\mathbf{P}_{t|t-1}^{-1}}
\end{aligned} }
\end{equation}
위 식의 기호를 단순화하여 다음과 같이 나타낸다
\begin{equation*} \begin{aligned}
\mathbf{x}
= \arg\min_{\mathbf{x}} \quad \left\| \mathbf{z} - \mathbf{H}\mathbf{x} \right\|^{2}_{\mathbf{R}} + \left\| \mathbf{c} + \mathbf{J}\mathbf{x} \right\|^{2}_{\mathbf{P}}
\end{aligned}
\end{equation*}
- $\mathbf{z} = \mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t-1}, 0, 0)$
- $\mathbf{c} = \hat{\mathbf{x}}_{t|t,j} - \hat{\mathbf{x}}_{t|t-1}$
- $\mathbf{R} = \mathbf{H}_{\mathbf{v}}\mathbf{R}^{-1}\mathbf{H}_{\mathbf{v}}^{\intercal}$
- $\mathbf{x} = \delta \hat{\mathbf{x}}$
위 식에서 norm을 전개하면 다음과 같다.
\begin{equation*} \begin{aligned}
\mathbf{x} = \arg\min_{\mathbf{x}} \ \bigg[ \underbrace{ (\mathbf{z} - \mathbf{H}\mathbf{x})^{\intercal}\mathbf{R}^{-1}(\mathbf{z} - \mathbf{H}\mathbf{x}) + (\mathbf{c} + \mathbf{J}\mathbf{x})^{\intercal}\mathbf{P}^{-1}(\mathbf{c} + \mathbf{J}\mathbf{x}) }_{\mathbf{r}} \bigg]
\end{aligned}
\end{equation*}
위 식에서 $\mathbf{r}$ 부분만 따로 전개하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{r} & = \mathbf{z}^{\intercal}\mathbf{R}^{-1}\mathbf{z} {\color{Mahogany} - \mathbf{x}^{\intercal}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z}- \mathbf{z}^{\intercal}\mathbf{R}^{-1}\mathbf{H}\mathbf{x} } + \mathbf{x}^{\intercal}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H}\mathbf{x} + \mathbf{c}^{\intercal}\mathbf{P}^{-1}\mathbf{c} + {\color{Mahogany} \mathbf{x}^{\intercal}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} + \mathbf{c}^{\intercal}\mathbf{P}^{-1}\mathbf{J}\mathbf{x} } + \mathbf{x}^{\intercal}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J}\mathbf{x} \\
& = \mathbf{z}^{\intercal}\mathbf{R}^{-1}\mathbf{z} {\color{Mahogany} - 2\mathbf{x}^{\intercal}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} } + \mathbf{x}^{\intercal}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H}\mathbf{x} + \mathbf{c}^{\intercal}\mathbf{P}^{-1}\mathbf{c} {\color{Mahogany} + 2\mathbf{x}^{\intercal}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} } + \mathbf{x}^{\intercal}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J}\mathbf{x}
\end{aligned}
\end{equation}
$\mathbf{r}$을 $\mathbf{x}$에 대해 편미분하면 다음과 같다.
\begin{equation} \label{eq:deriveieskf1}
\begin{aligned}
\frac{\partial \mathbf{r}}{\partial {\mathbf{x}}} = - \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} + \mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H}\mathbf{x} +\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} + \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J}\mathbf{x} & = 0 \\
{\color{Mahogany} (\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J}) } \mathbf{x} & =
\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} - \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} \\
\mathbf{x} & = {\color{Mahogany}(\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J})^{-1} } (
\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} - \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c})
\end{aligned}
\end{equation}
$(\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H} + \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J})^{-1}$ 부분은 matrix inversion lemma를 통해 다음과 같이 전개할 수 있다.
\begin{equation}
\begin{aligned}
{\color{Mahogany}(\underbrace{\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{J}}_{\bar{\mathbf{P}}^{-1}} +\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{H})^{-1} = (\bar{\mathbf{P}} -\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}} }
\end{aligned}
\end{equation}
- $\bar{\mathbf{P}} = \mathbf{J}^{-1}\mathbf{P}\mathbf{J}^{-\intercal}$로 치환
Matrix Inversion Lemma
$(\mathbf{A}+\mathbf{UCV})^{-1}=\mathbf{A}^{-1}-\mathbf{A}^{-1}\mathbf{U}(\mathbf{C}^{-1}+\mathbf{VA}^{-1}\mathbf{U})^{-1}\mathbf{VA}^{-1}$
위 식을 (\ref{eq:deriveieskf1}) 식에 대입하면 다음과 같다.
\begin{equation}
\begin{aligned}
{\mathbf{x}} = {\color{Mahogany}(\bar{\mathbf{P}} -\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}})} (
\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} - \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c})
\end{aligned}
\end{equation}
위 식을 전개하면 다음과 같다
\begin{equation}
\begin{aligned}
{\mathbf{x}} & = (\bar{\mathbf{P}} -\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}})(
\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} - \mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c}) \\
& = \bar{\mathbf{P}}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} - \bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c}
-\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + {\color{Mahogany} \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1} } \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal}\mathbf{R}^{-1} \mathbf{z} +\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} \\
& = \bar{\mathbf{P}}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} - \bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c}
-\bar{\mathbf{P}}\mathbf{H}^{\intercal} \cancel{ (\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1} } ({\color{Mahogany} \cancel{ (\mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal}+\mathbf{R})} \mathbf{R}^{-1} - \mathbf{I}) } \mathbf{z} +\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} \\
& = \cancel{ \bar{\mathbf{P}}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} } - \bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c}
- \cancel{ \bar{\mathbf{P}}\mathbf{H}^{\intercal}\mathbf{R}^{-1}\mathbf{z} } + \bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{z} +\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} \\
& = - \bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c}
+ \bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{z} +\bar{\mathbf{P}}\mathbf{H}^{\intercal}(\mathbf{R} + \mathbf{H}\bar{\mathbf{P}}\mathbf{H}^{\intercal})^{-1}\mathbf{H}\bar{\mathbf{P}}\mathbf{J}^{\intercal}\mathbf{P}^{-1}\mathbf{c} \\
& = - \mathbf{J}^{-1}\underbrace{\mathbf{P}\mathbf{J}^{-\intercal}\mathbf{J}^{\intercal}\mathbf{P}^{-1}}_{\mathbf{I}} \mathbf{c}
+ {\color{Cyan} \mathbf{J}^{-1}\mathbf{P}\mathbf{J}^{-\intercal}\mathbf{H}^{\intercal}( \underbrace{\mathbf{R} + \mathbf{H}\mathbf{J}^{-1}\mathbf{P}\mathbf{J}^{-\intercal}\mathbf{H}^{\intercal}}_{\mathbf{S}})^{-1} } \mathbf{z} +{\color{Cyan} \mathbf{J}^{-1}\mathbf{P}\mathbf{J}^{-\intercal}\mathbf{H}^{\intercal}(\underbrace{\mathbf{R} + \mathbf{H}\mathbf{J}^{-1}\mathbf{P}\mathbf{J}^{-\intercal}\mathbf{H}^{\intercal}}_{\mathbf{S}})^{-1} } \mathbf{HJ}^{-1}\underbrace{\mathbf{PJ}^{-\intercal}\mathbf{J}^{\intercal}\mathbf{P}^{-1}}_{\mathbf{I}} \mathbf{c} \\
& = {\color{Cyan} \mathbf{K} } \mathbf{z} + {\color{Cyan} \mathbf{K} } \mathbf{H}\mathbf{J}^{-1}\mathbf{c} - \mathbf{J}^{-1}\mathbf{c}
\end{aligned}
\end{equation}
- $\mathbf{K} = \mathbf{J}^{-1}\mathbf{PJ}^{-\intercal}\mathbf{H}^{\intercal}\mathbf{S}^{-1}$
위 마지막 줄의 식에서 치환했던 기호를 복원하면 다음과 같이 최종 업데이트 식 (\ref{eq:ieskf8})를 얻을 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\therefore \delta \hat{\mathbf{x}}_{t|t,j} = \mathbf{K}_{t,j} \bigg( \mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t,j}, 0 ,0) + \mathbf{H}_{t,j}\mathbf{J}^{-1}_{t,j}(\hat{\mathbf{x}}_{t|t,j} - \hat{\mathbf{x}}_{t|t-1}) \bigg) - \mathbf{J}^{-1}_{t,j}(\hat{\mathbf{x}}_{t|t,j} - \hat{\mathbf{x}}_{t|t-1})
\end{aligned} }
\end{equation}
- $\mathbf{z} = \mathbf{z}_{t} - \mathbf{h}(\hat{\mathbf{x}}_{t|t-1}, 0, 0)$
- $\mathbf{c} = \hat{\mathbf{x}}_{t|t,j} - \hat{\mathbf{x}}_{t|t-1}$
- $\mathbf{R} = \mathbf{H}_{\mathbf{v}}\mathbf{R}^{-1}\mathbf{H}_{\mathbf{v}}^{\intercal}$
- $\mathbf{x} = \delta \hat{\mathbf{x}}$
지금까지의 유도 과정을 그림으로 나타내면 다음과 같다.


Wrap-up
지금까지 설명한 KF, EKF, ESKF, IEKF, IESKF를 한 장의 슬라이드로 표현하면 다음과 같다. 클릭하면 큰 그림으로 볼 수 있다.
Kalman Filter (KF)

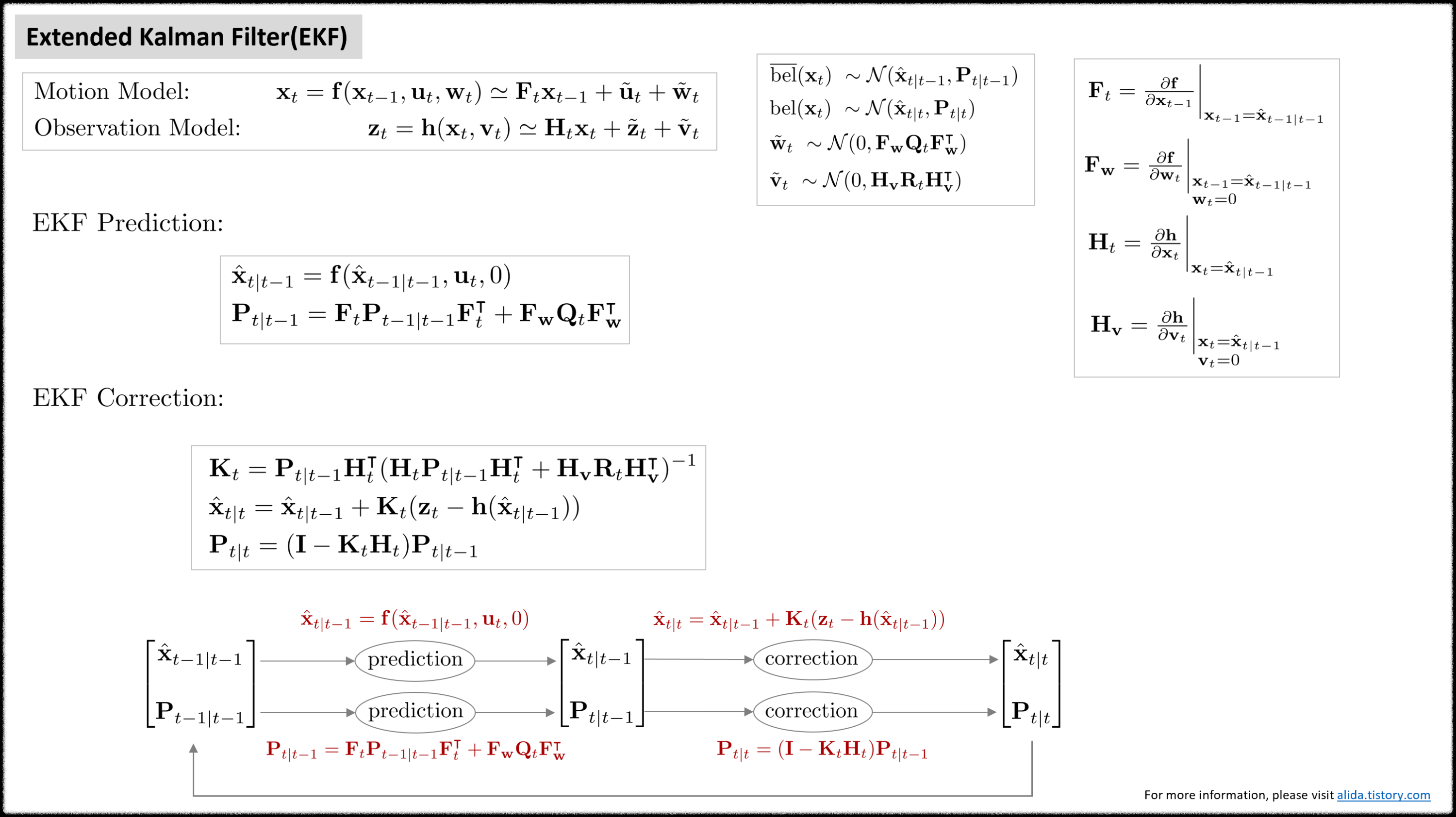
Extended Kalman Filter (EKF)
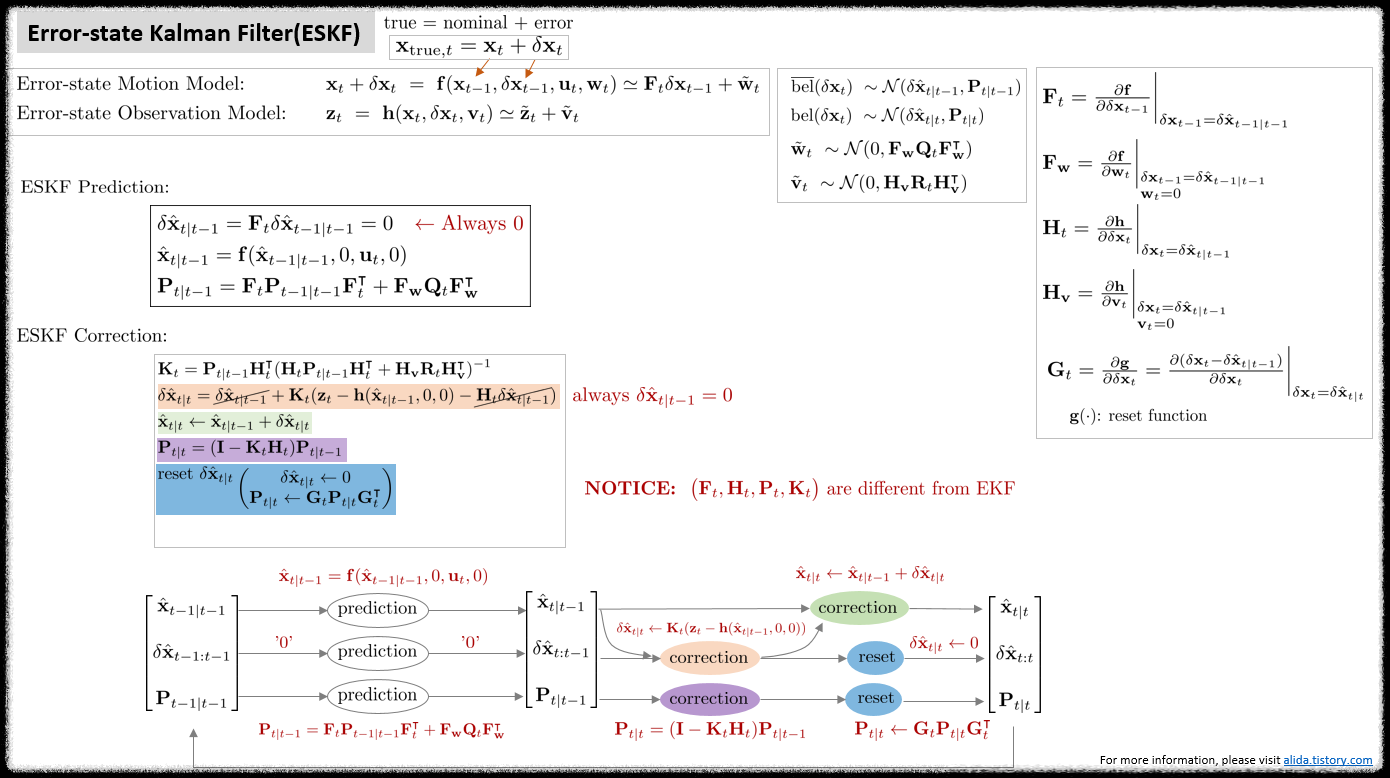
Error-state Kalman Filter (ESKF)
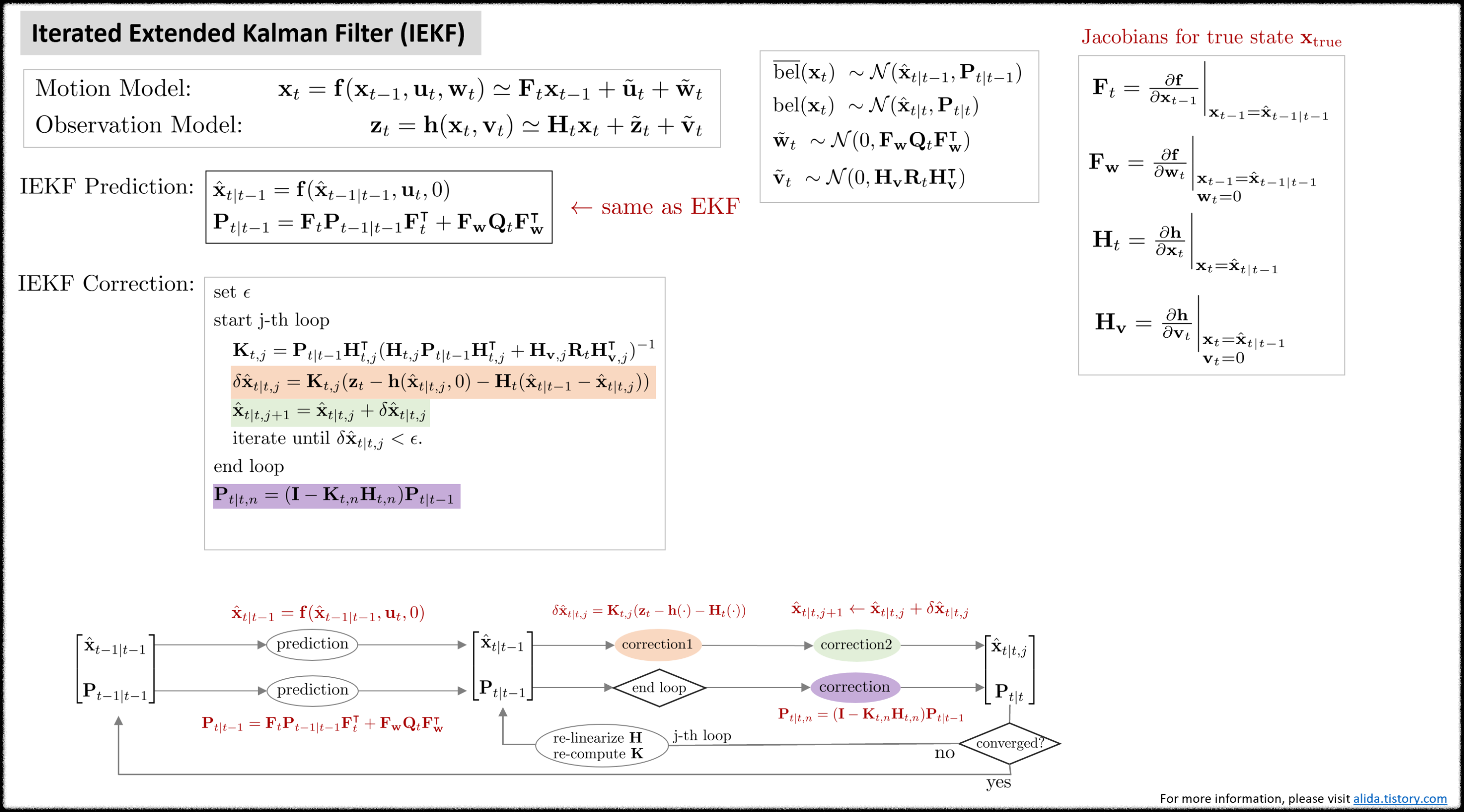
Iterated Extended Kalman Filter (IEKF)
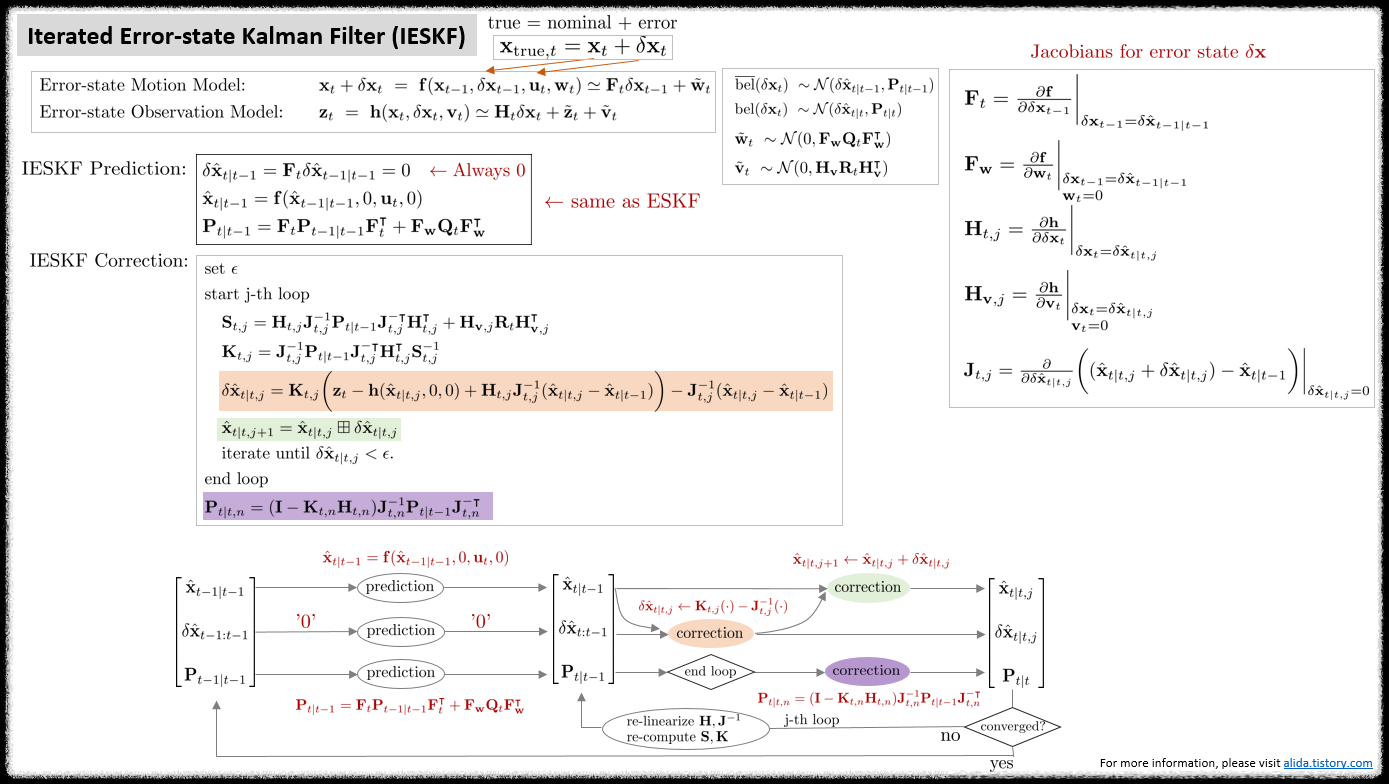
Iterated Error-state Kalman Filter (IESKF)
References
[1] Kalman Filter - Wikipedia
[2] (Paper) Sola, Joan. "Quaternion kinematics for the error-state Kalman filter." arXiv preprint arXiv:1711.02508 (2017).
[3] (Youtube) Robot Mapping Coure - Freiburg Univ
[4] (Blog) [SLAM] Kalman filter and EKF(Extended Kalman Filter) - jinyongjeong
[5] (Blog) Error-State Kalman Filter understanding and formula derivation - CSDN
[6] (Paper) He, Dongjiao, Wei Xu, and Fu Zhang. "Kalman filters on differentiable manifolds." arXiv preprint arXiv:2102.03804 (2021).
[7] (Book) SLAM in Autonomous Driving book (SAD book)
[8] (Paper) Xu, Wei, and Fu Zhang. "Fast-lio: A fast, robust lidar-inertial odometry package by tightly-coupled iterated kalman filter." IEEE Robotics and Automation Letters 6.2 (2021): 3317-3324.
[9] (Paper) Huai, Jianzhu, and Xiang Gao. "A Quick Guide for the Iterated Extended Kalman Filter on Manifolds." arXiv preprint arXiv:2307.09237 (2023).
[10] (Paper) Bloesch, Michael, et al. "Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback." The International Journal of Robotics Research 36.10 (2017): 1053-1072.
[11] (Paper) Skoglund, Martin A., Gustaf Hendeby, and Daniel Axehill. "Extended Kalman filter modifications based on an optimization view point." 2015 18th International Conference on Information Fusion (Fusion). IEEE, 2015.
[12] (Blog) From MAP, MLE, OLS, GN to IEKF, EKF
[13] (Book) Thrun, Sebastian. "Probabilistic robotics." Communications of the ACM 45.3 (2002): 52-57.
 A L I D A
A L I D A





