ICP Animation (Left Mouse : Drag, Right Mouse : Rotate, Wheel : Zoom)
Introduction
Iterative Closest Point (ICP) 알고리즘은 두 점군(pointcloud) 집합들이 주어졌을 때 각 점으로부터 최단 거리의 점들을 탐색하여 이를 바탕으로 반복적으로 정합(registration)하는 방법을 말한다. ICP는 주로 LiDAR SLAM에서 3D 스캔 데이터 정렬에 사용되며 Point-to-Point, Point-to-Plane 기법 등이 존재한다.
Example pointcloud data (2D)
2D Example (Left Mouse : Drag, Right Mouse : Rotate, Wheel : Zoom)

우선 2D 점군 데이터를 예시로 들어보자. 로봇이 2D 스캐너를 통해 다음과 같은 데이터를 $t$, $t+1$ 시점에 대해 획득하였다고 가정하자.
$t$ 시점의 포인트(빨간색)과 $t+1$ 시점의 포인트(파란색)의 2D 점군의 좌표는 다음과 같다.
sourcePoints = [ [-19, -15], [-18, -10], [-15, -9], [-14, -7], [-11, -6], [-9, -5], [-7, -6], [-4, -8], [-1, -11], [0, -14], [1, -17], [5, -20], [9, -24], [10, -25], [13, -24], [14, -25], [17, -25], [19, -22], [22, -18], [23, -16] ]
targetPoints = [ [-12, -8], [-12, -2], [-10, 1], [-10, 4], [-9, 6], [-6, 7], [-3, 8], [-1, 8], [3, 6], [6, 5], [10, 3], [14, 1], [17, 1], [19, 0], [22, 1], [24, 2], [27, 4], [26, 7], [27, 11], [27, 15] ]
Example pointcloud data (3D)
3D Example (Left Mouse : Drag, Right Mouse : Rotate, Wheel : Zoom)
하지만 실제 주어지는 데이터는 일반적으로 다음과 같은 3D 점군 데이터가 주어진다. 로봇이 3D 스캐너를 통해 다음과 같은 데이터를 $t$, $t+1$ 시점에 대해 획득하였다고 가정하자.
$t$ 시점의 포인트(빨간색)과 $t+1$ 시점의 포인트(파란색)의 3D 점군의 좌표는 다음과 같다.
sourcePoints = [ [-19, -15, 7], [-18, -10, 6], [-15, -9, 5], [-14, -7, 4], [-11, -6, 8], [-9, -5, 5], [-7, -6, 7], [-4, -8, 6], [-1, -11, 4], [0, -14, 6], [1, -17, 8], [5, -20, 7], [9, -24, 5], [10, -25, 6], [13, -24, 8], [14, -25, 5], [17, -25, 7], [19, -22, 6], [22, -18, 8], [23, -16, 7] ]
targetPoints = [ [-12, -8, 9], [-12, -2, 11], [-10, 1, 10], [-10, 4, 12], [-9, 6, 9], [-6, 7, 10], [-3, 8, 8], [-1, 8, 12], [3, 6, 11], [6, 5, 9], [10, 3, 8], [14, 1, 12], [17, 1, 11], [19, 0, 10], [22, 1, 8], [24, 2, 9], [27, 4, 11], [26, 7, 12], [27, 11, 9], [27, 15, 10] ]
Point-to-point ICP
With known data associations
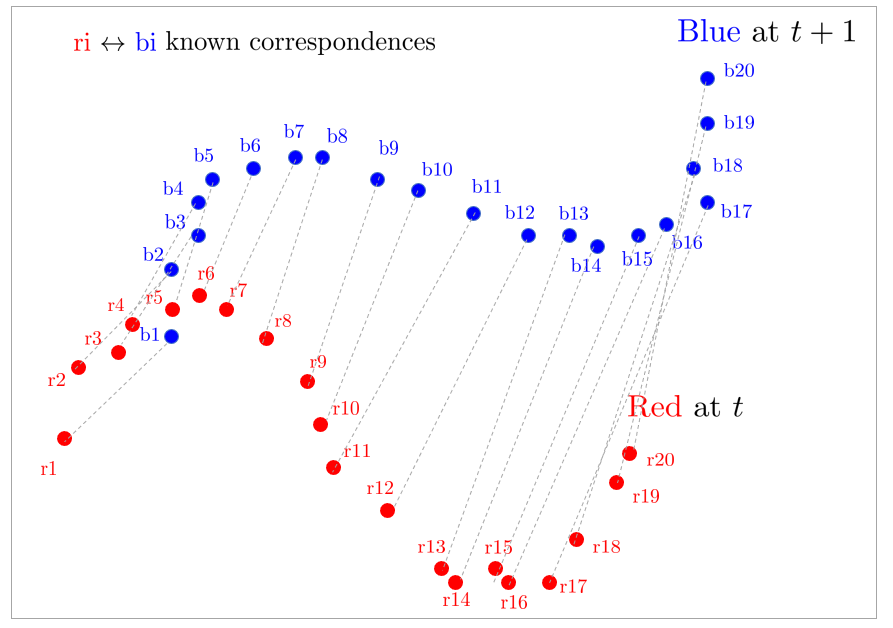
ICP를 본격적으로 설명하기에 앞서 가장 쉬운 케이스를 먼저 생각해보자. 만약 위 그림과 같이 두 점군의 데이터들 간 관계(association, correspondence) ${\color{Red}r_i} \leftrightarrow {\color{Cyan}b_i}$가 미리 주어져 있는 경우 해당 정합 문제는 closed form 해가 존재하여 간단하게 문제를 풀 수 있다. (No initial guess, no iterative)
빨간색 점군을 ${\color{Red} \mathbf{p}_{t}} = [\mathbf{p}_{t,1}, \mathbf{p}_{t,2}, \cdots, \mathbf{p}_{t,n}]^{\intercal}$ 파란색 점군을 ${\color{Cyan}\mathbf{p}_{t+1}} = [\mathbf{p}_{t+1,1}, \mathbf{p}_{t+1,2}, \cdots, \mathbf{p}_{t+1,n}]^{\intercal}$라고 하면 두 점군 사이의 관계는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
{\color{Cyan}\mathbf{p}_{t+1}} \approx \mathbf{R} {\color{Red}\mathbf{p}_{t}} + \mathbf{t}
\end{aligned}
\end{equation}
- 위 식은 2D, 3D 데이터 $\mathbf{p}_{t}$에 대해 모두 성립한다. 따라서 $\mathbf{R} \in SO(2)$와 $\mathbf{R} \in SO(3)$ 모두 성립한다.
위 식은 다음과 같은 최소제곱법 문제로 변환할 수 있다.
\begin{equation} \label{eq:dataasso1}
\boxed{ \begin{aligned}
\arg\min_{\mathbf{R},\mathbf{t}} \| {\color{Cyan}\mathbf{p}_{t+1}} - \mathbf{R} {\color{Red} \mathbf{p}_{t}} - \mathbf{t} \|^2
\end{aligned} }
\end{equation}
위 최소제곱법 문제는 비선형 항 $\mathbf{R}$가 포함되어 있기 때문에 정규방정식(normal equation) 형태로 풀 수 없다. 따라서 이를 해결하기 위해 공분산 행렬을 SVD 분해하는 방법과 비선형 최소제곱법(Gauss-Newton)으로 푸는 방법이 존재한다. 우선 공분산 행렬을 SVD 분해하는 방법에 대해 먼저 설명한다.
Covariance SVD-based solution
결론부터 말하자면 두 점군에 대한 공분산 행렬 $\mathbf{C}$를 구한 후 이를 SVD 분해하여 회전 행렬의 최적해 $\mathbf{R}^*$를 구할 수 있다.
우선 이를 위해 두 점군의 무게 중심(centroid)를 먼저 구한다.
\begin{equation}
\begin{aligned}
& \bar{\mathbf{p}}_t = \frac{1}{n} \sum \mathbf{p}_{t,i} \\
& \bar{\mathbf{p}}_{t+1} = \frac{1}{n} \sum \mathbf{p}_{t+1,i} \\
\end{aligned}
\end{equation}
다음으로 기존의 모든 점들 $\mathbf{p}$에 대해 무게 중심 $\bar{\mathbf{p}}$을 빼준 $\mathbf{p}'$ 값을 구한다.
\begin{equation}
\begin{aligned}
& \mathbf{p}'_t = \mathbf{p}_t - \bar{\mathbf{p}}_t \\
& \mathbf{p}'_{t+1} = \mathbf{p}_{t+1} - \bar{\mathbf{p}}_{t+1} \\
\end{aligned}
\end{equation}
위 결과를 사용하여 (\ref{eq:dataasso1}) 식을 다시 표현하면 다음과 같다.
\begin{equation} \label{eq:svd1}
\begin{aligned}
\arg\min_{\mathbf{R},\mathbf{t}} \| (\mathbf{p}'_{t+1} + \bar{\mathbf{p}}_{t+1}) - \mathbf{R} (\mathbf{p}'_{t} + \bar{\mathbf{p}}_{t}) - \mathbf{t} \|^2
\end{aligned}
\end{equation}
- $\mathbf{p}_{t+1} = \mathbf{p}'_{t+1} + \bar{\mathbf{p}}_{t+1}$
- $\mathbf{p}_{t} = \mathbf{p}'_{t} + \bar{\mathbf{p}}_{t}$
이 때, 두 점군의 이동 벡터 $\mathbf{t}$는 $t+1$시점 점군의 무게중심 $\bar{\mathbf{p}}_{t+1}$과 $t$ 시점 회전한 점군의 무게중심 $\mathbf{R}\bar{\mathbf{p}}_{t}$의 차이로 설정한다. 즉, 두 점군의 상대 회전량을 정확히 보정한다면 두 점군은 정확히 $\mathbf{t}$만큼 떨어져 있다고 가정하는 것이다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{t} = \bar{\mathbf{p}}_{t+1} - \mathbf{R}\bar{\mathbf{p}}_{t}
\end{aligned} }
\end{equation}
(\ref{eq:svd1})에 위 식을 대입하면 다음과 같이 $\mathbf{t}$ 항이 소거되어 $\mathbf{R}$을 찾는 문제로 단순화된다.
\begin{equation}
\begin{aligned}
\arg\min_{\mathbf{R}} \| \mathbf{p}'_{t+1} - \mathbf{R} \mathbf{p}'_{t} \|^2
\end{aligned}
\end{equation}
위 식을 전개하면 다음과 같다. 식이 전개되면서 $\mathbf{R}$이 소거되어 중간의 항만 $\mathbf{R}$과 관련있는 항이 된다.
\begin{equation}
\begin{aligned}
\arg\min_{\mathbf{R}} \left\| \mathbf{p}'_{t+1} - \mathbf{R} \mathbf{p}'_{t} \right\|^{2} & = \arg\min_{\mathbf{R}} \bigg[ \mathbf{p}_{t+1}^{'\intercal}\mathbf{p}'_{t+1} {\color{Mahogany} - 2 \mathbf{p}^{'\intercal}_{t+1} \mathbf{R}\mathbf{p}'_{t} } + \mathbf{p}_t^{'\intercal} \underbrace{\mathbf{R}^{\intercal} \mathbf{R}}_{\mathbf{I}} \mathbf{p}'_{t} \bigg] \\
& = \arg\min_{\mathbf{R}} \bigg[ {\color{Mahogany} -2\mathbf{p}^{'\intercal}_{t+1} \mathbf{R}\mathbf{p}'_{t} } + C \bigg]
\end{aligned}
\end{equation}
따라서 최적화 수식은 다음과 같이 다시 쓸 수 있다. 마이너스 부호($-$)가 사라지면서 argmin 문제가 argmax 문제로 변환된다.
\begin{equation}
\begin{aligned}
\mathbf{R}^* & = \arg\min_{\mathbf{R}} \Big[ -2\mathbf{p}^{'\intercal}_{t+1} \mathbf{R}\mathbf{p}'_{t} \Big] \\
& = \arg\max_{\mathbf{R}} \Big[ \mathbf{p}^{'\intercal}_{t+1} \mathbf{R}\mathbf{p}'_{t} \Big] \\
& = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{p}^{'\intercal}_{t+1} \mathbf{R}\mathbf{p}'_{t}) \Big] \\
& = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{R} {\color{Mahogany} \mathbf{p}'_{t}\mathbf{p}^{'\intercal}_{t+1} } ) \Big] \quad \leftarrow \because \text{tr}(\mathbf{AB}) = \text{tr}(\mathbf{BA}) \\
& = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{R} {\color{Mahogany} \mathbf{C} } ) \Big]
\end{aligned}
\end{equation}
- $\mathbf{C} = \mathbf{p}'_{t}\mathbf{p}^{'\intercal}_{t+1}$
위 식의 세번째 줄을 보면 $\mathbf{p}^{'\intercal}_{t+1} \mathbf{R}\mathbf{p}'_{t} = \mathbb{R}^{1\times n}\cdot \mathbb{R}^{n\times n} \cdot \mathbb{R}^{n\times 1} = \mathbb{R}$로 스칼라 값이 나오는 것을 알 수 있다. 따라서 최종 결과가 스칼라(=1x1 행렬)이므로 행렬의 대각 성분의 합인 trace의 유용한 성질을 활용할 수 있다. $\text{tr}(\mathbf{AB}) = \text{tr}(\mathbf{BA})$의 성질을 활용하여 $\mathbf{A} = \mathbf{p}^{'\intercal}_{t+1}$과 $\mathbf{B}=\mathbf{R}\mathbf{p}'_{t}$의 위치를 바꿔준다.
위 식의 네번째 줄을 보면 ${\color{Mahogany} \mathbf{p}'_{t}\mathbf{p}^{'\intercal}_{t+1} }$ 식은 두 점군의 공분산 행렬(covariance matrix)의 정의와 동일하다. 따라서 이를 $\color{Mahogany} \mathbf{C}$로 치환해준다.
Covariance matrix of $\mathbf{x}, \mathbf{y}$
두 데이터 집합 $\mathbf{x} = [\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_{n}]^{\intercal}$과
$\mathbf{y} = [\mathbf{y}_1, \mathbf{y}_2, \cdots, \mathbf{y}_{n}]^{\intercal}$이 주어졌을 때 두 데이터의 공분산 행렬은 다음과 같이 구할 수 있다.
1. 두 데이터의 평균을 구한다
\begin{equation} \begin{aligned} &\bar{\mathbf{x}} = \frac{1}{n} \sum \mathbf{x}_i \\ & \bar{\mathbf{y}} = \frac{1}{n} \sum \mathbf{y}_i \\ \end{aligned} \end{equation}
2. 원본 데이터에서 각각 평균을 빼준다
\begin{equation} \begin{aligned} & {\mathbf{x}}' = {\mathbf{x}} - \bar{\mathbf{x}} \\ & {\mathbf{y}}' = {\mathbf{y}} - \bar{\mathbf{y}} \\ \end{aligned} \end{equation}
3. 두 데이터의 공분산 행렬 $\mathbf{C}_{\mathbf{xy}}$은 다음과 같이 구할 수 있다
\begin{equation} \begin{aligned} \mathbf{C}_{\mathbf{xy}} & = {\mathbf{x}}'{\mathbf{y}}^{'\intercal} \\ & = ({\mathbf{x}} - \bar{\mathbf{x}})({\mathbf{y}} - \bar{\mathbf{y}})^{\intercal} \end{aligned} \end{equation}
따라서 최적의 $\mathbf{R}^*$을 구하기 위해서는 다음 식을 풀어야 한다.
\begin{equation} \label{eq:svd2}
\begin{aligned}
\mathbf{R}^* & = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{R} \mathbf{C} ) \Big] \\
& = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{R} \mathbf{UDV}^{\intercal} ) \Big]
\end{aligned}
\end{equation}
공분산 행렬 $\mathbf{C}$은 값이 마이너스($-$)가 나올 수 없으므로 항상 positive (semi-)definite 행렬이다. 따라서 위 식의 두번째 줄에서 $\mathbf{C}$를 SVD 분해하면 모든 특이값(singular value)는 항상 0보다 크거나 같다.
Method 1 for $\mathbf{R}^*$
Lemma
임의의 postive definite 행렬 $\mathbf{AA}^{\intercal}$과 정규직교행렬(orthonormal) $\mathbf{B}$에 대하여 다음과 같은 Cauchy-Schwarz 부등식이 성립한다.
\begin{equation}\begin{aligned} \text{tr}(\mathbf{AA}^{\intercal}) \ge \text{tr}(\mathbf{BAA}^{\intercal})\end{aligned}\end{equation}
Proof
임의의 벡터에 대한 Cauchy-Schwarz 부등식은 다음과 같다.
\begin{equation} \begin{aligned} | \langle \mathbf{u}, \mathbf{v} \rangle \le \| \mathbf{u} \| \cdot \| \mathbf{v} \| \end{aligned} \end{equation}
- $\mathbf{u}, \mathbf{v}$: 임의의 벡터
- $\langle \cdot, \cdot \rangle$: 벡터의 내적(inner product)
- $\| \mathbf{a} \| = \sqrt{\langle \mathbf{a}, \mathbf{a} \rangle}$: 벡터의 놈(norm)
$\text{tr}(\mathbf{BAA}^{\intercal})$은 다음과 같이 벡터 형태로 표현이 가능하다
\begin{equation} \begin{aligned} \text{tr}(\underline{ \mathbf{BA}} \cdot \underline{\underline{ \mathbf{A}^{\intercal}}}) & = \text{tr}(\underline{\underline{ \mathbf{A}^{\intercal}}} \cdot \underline{ \mathbf{BA} }) \\ & = \sum \mathbf{a}_i^{\intercal}\mathbf{B}\mathbf{a}_i \end{aligned} \end{equation}
위 식을 Cauchy-Schwarz 부등식에 대입하면 다음과 같은 식을 얻는다.
\begin{equation} \begin{aligned} \mathbf{a}^{\intercal}_i \mathbf{B} \mathbf{a}_i & \le \sqrt{(\mathbf{a}_{i}^{\intercal} \mathbf{a}_{i}) (\mathbf{a}_{i}^{\intercal} \underbrace{\mathbf{B}^{\intercal}\mathbf{B}}_{\mathbf{I}} \mathbf{a}_i)} \\ & = \mathbf{a}^{\intercal}_i \mathbf{a}_i \end{aligned} \end{equation} \begin{equation} \begin{aligned} \mathbf{a}^{\intercal}_i \mathbf{B} \mathbf{a}_i & \le \mathbf{a}^{\intercal}_i \mathbf{a}_i \end{aligned} \end{equation}
따라서 다음과 같은 Lemma를 얻는다.
\begin{equation}\boxed{ \begin{aligned} \therefore \text{tr}(\mathbf{AA}^{\intercal}) \ge \text{tr}(\mathbf{BAA}^{\intercal}) \end{aligned} } \end{equation}
만약 $\mathbf{R} = \mathbf{V}\mathbf{U}^{\intercal}$로 정의하면 (\ref{eq:svd2})에서 정규직교행렬 $\mathbf{U}^{\intercal}\mathbf{U}$가 서로 소거되어 $\mathbf{V}\mathbf{D}\mathbf{V}^{\intercal}$만 남는다. 이를 통해 $\mathbf{AA}^{\intercal}$ 형태로 만들 수 있다.
\begin{equation}\boxed{ \begin{aligned}
\text{tr}(\mathbf{R}\mathbf{U}\mathbf{D}\mathbf{V}^{\intercal}) & = \text{tr}(\mathbf{V} \underbrace{ \mathbf{U}^{\intercal}\mathbf{U}}_{\mathbf{I}} \mathbf{D}\mathbf{V}^{\intercal}) \\
& = \text{tr}(\mathbf{V}\mathbf{D}\mathbf{V}^{\intercal}) \\
& = \text{tr}(\mathbf{V}\mathbf{D}^{\frac{1}{2}}\mathbf{D}^{\frac{1}{2}}\mathbf{V}^{\intercal}) \\
& = \text{tr}(\mathbf{V}\mathbf{D}^{\frac{1}{2}})(\mathbf{D}^{\frac{1}{2}}\mathbf{V}^{\intercal}) \quad \leftarrow \mathbf{AA}^{\intercal} \text{ form } \\
& = \text{tr}(\mathbf{AA}^{\intercal}) \\
& \ge \text{tr}(\mathbf{R}'\mathbf{AA}^{\intercal})
\end{aligned} } \end{equation}
- $\mathbf{R}'$: 임의의 정규직교행렬(orthonormal)
- $\mathbf{A} = \mathbf{V}\mathbf{D}^{\frac{1}{2}}$
이를 다시 정리하면 다음과 같다.
\begin{equation}\boxed{ \begin{aligned}
\text{tr}(\mathbf{R}\mathbf{C}) = \text{tr}(\mathbf{VU}^{\intercal}\mathbf{C})& \ge \text{tr}(\mathbf{R}'\mathbf{AA}^{\intercal}) = \text{tr}(\mathbf{R}'\mathbf{R}\mathbf{C})
\end{aligned} } \end{equation}
위 식의 의미는 $\mathbf{R}$은 $\mathbf{R}=\mathbf{VU}^{\intercal}$인 경우에 모든 다른 임의의 회전행렬 $\mathbf{R}'\mathbf{R}$보다 큰 값을 가진다는 의미이다. 따라서 argmax의 해가 된다.
\begin{equation} \label{eq:svd3} \boxed{ \begin{aligned}
& \mathbf{R} = \mathbf{V}\mathbf{U}^{\intercal} \\
& \mathbf{t} =\mathbf{R}\bar{\mathbf{p}}_{t} - \bar{\mathbf{p}}_{t+1}
\end{aligned} } \end{equation}
Method 2 for $\mathbf{R}^*$
(\ref{eq:svd2}) 식을 다시 보면 trace 내부의 값을 최대화해야 한다. 이 때, 앞서 언급했듯이 공분산 행렬 $\mathbf{C}$는 positive (semi-)definite 행렬이므로 특이값이 항상 0보다 크거나 같고 따라서 대각행렬 $\mathbf{D}$의 모든 값은 항상 0보다 크거나 같다. 그리고 $\mathbf{R}, \mathbf{U}, \mathbf{V}$는 정규직교행렬(orthonormal) 행렬이므로 대각행렬과 곱해지면 항상 trace 값은 $\mathbf{D}$ 자체보다 작아지게 된다.
\begin{equation} \begin{aligned}
\text{tr}(\mathbf{D}) \ge \text{tr}(\mathbf{RUDV}^{\intercal})
\end{aligned} \end{equation}
Trace 성질에 의해 순서를 바꿔주게 되면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{R}^* & = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\underline{\underline{\mathbf{RU}}} \cdot \underline{\mathbf{DV}^{\intercal}} ) \Big] \\
& = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\underline{\mathbf{DV}^{\intercal}} \cdot \underline{\underline{\mathbf{RU} }} ) \Big]
\end{aligned}
\end{equation}
만약 $\mathbf{R} = \mathbf{VU}^{\intercal}$인 경우 정규직교행렬들이 소거되어 최대 trace 값을 가진다.
\begin{equation}
\begin{aligned}
\mathbf{R}^* & = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{DV}^{\intercal} \mathbf{RU} ) \Big] \\
& = \arg\max_{\mathbf{R}} \Big[ \text{tr}(\mathbf{D} \underbrace{\mathbf{V}^{\intercal}\mathbf{RU}}_{\mathbf{I}} ) \Big] \\
\end{aligned}
\end{equation}
- $\mathbf{R} = \mathbf{VU}^{\intercal}$
따라서 앞서 method1에서 유도한 (\ref{eq:svd3})와 동일한 $\mathbf{R}$ 값을 구할 수 있다.
\begin{equation}\boxed{ \begin{aligned}
& \mathbf{R} = \mathbf{V}\mathbf{U}^{\intercal} \\
& \mathbf{t} = \bar{\mathbf{p}}_{t+1} - \mathbf{R}\bar{\mathbf{p}}_{t}
\end{aligned} } \end{equation}
회전행렬의 최적해를 구할 때 $\mathbf{R}$이 SO(3)군의 조건을 만족하려면 반드시 행렬식이 $+1$이어야 한다. $\text{det}(\mathbf{R})=1$. 하지만 실제 ICP 해를 구하다보면 행렬식이 $-1$이 되는 경우가 발생하는데 이는 reflection (특정 축 기준으로 상하좌우 반전)이 된 경우이다. 이러한 degenerate 케이스를 방지하기 위해 일반적으로 다음과 같이 회전 행렬의 최적해를 구한다.
\begin{equation}
\begin{aligned}
\mathbf{R} = \mathbf{V} \begin{bmatrix} 1 && \\ &1& \\ && \text{det}(\mathbf{VU}^{\intercal}) \end{bmatrix} \mathbf{U}^{\intercal}
\end{aligned}
\end{equation}
With unknown data associations
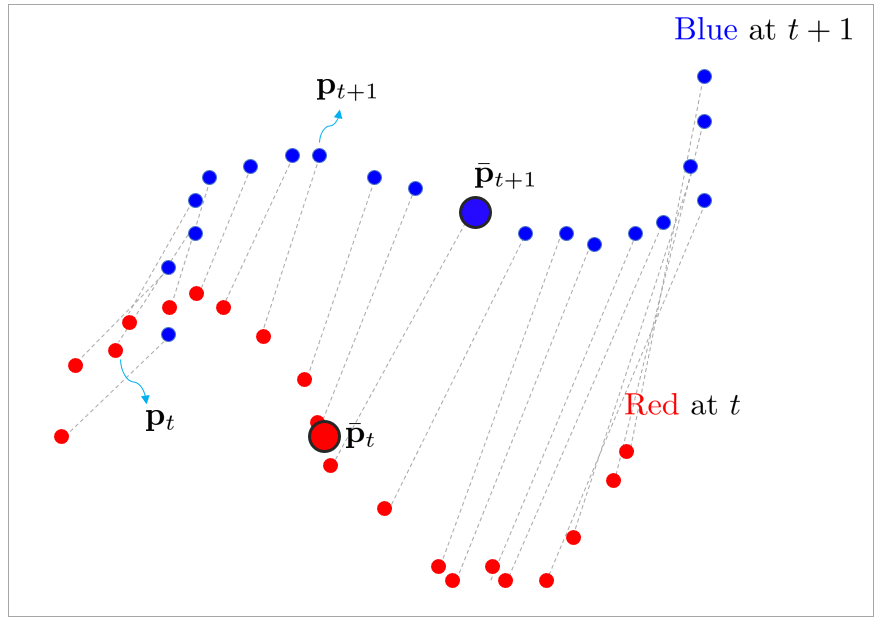
이전 섹션에서 살펴본 최적해 $\mathbf{R}^*, \mathbf{t}^*$는 두 점군 사이의 대응 관계(association, correspondences)를 모두 알고 있는 경우에 사용할 수 있는 방법이었다. 하지만 일반적으로 센서에서 얻어지는 두 점군 데이터는 어느 포인트가 어느 포인트와 대응하는지 알 수 없다.

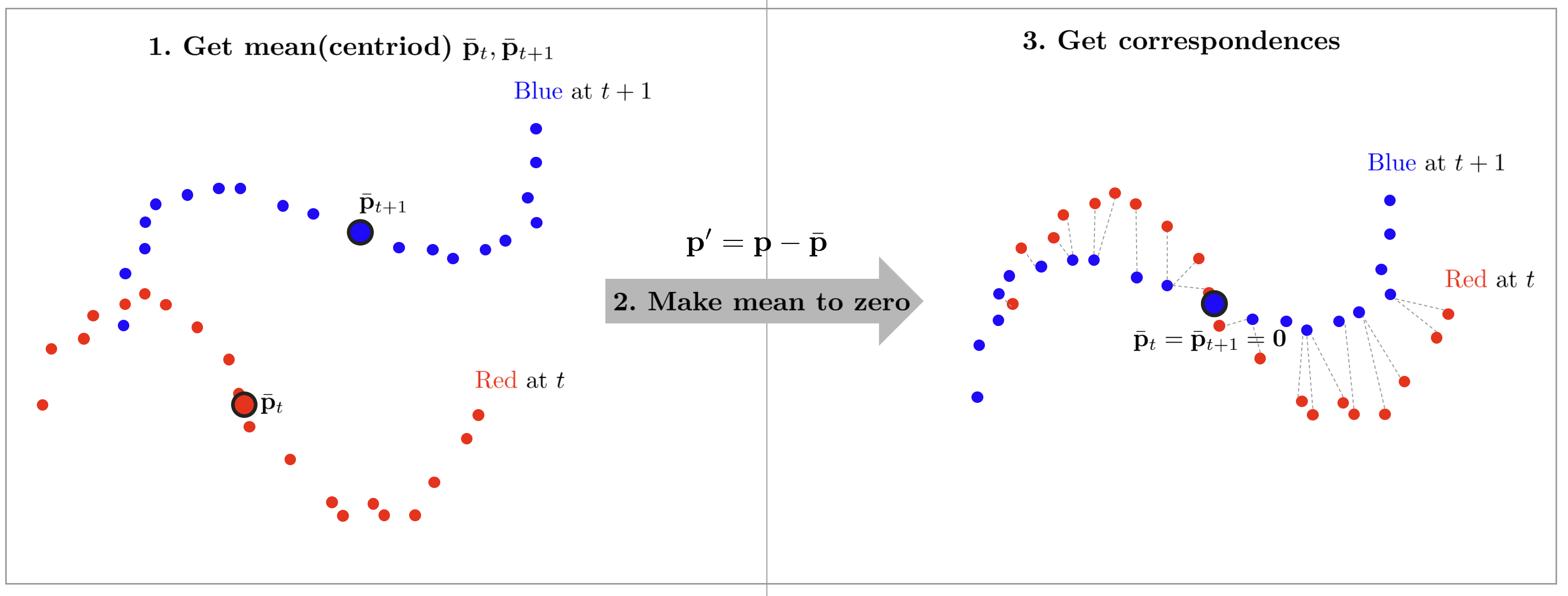
위와 같이 대응 관계를 모르는 경우, 바로 구할 수 있는 closed form 해는 존재하지 않는다. 따라서 하나의 점으로부터 가장 가까운 점(closest point)을 대응점 쌍으로 설정하여 반복적(iterative)으로 최적해를 구하는 알고리즘이 Iterative Closest Point(ICP)이다. ICP의 전체적인 과정은 다음과 같다. ($j$: 현재 반복 횟수)
- source 점군과 target 점군의 평균(또는 centroid) $\bar{\mathbf{p}}_t, \bar{\mathbf{p}}_{t+1}$를 구한다.
- 각 점군에 두 평균을 빼줌으로써 평균을 0으로 정규화한다. ($\mathbf{p}' = \mathbf{p} - \bar{\mathbf{p}}$)
- 각 source 점들마다 최단 거리의 target 점들을 correspondence로 설정한다. (nearest neighborhood 알고리즘 사용 e.g., KD-tree)
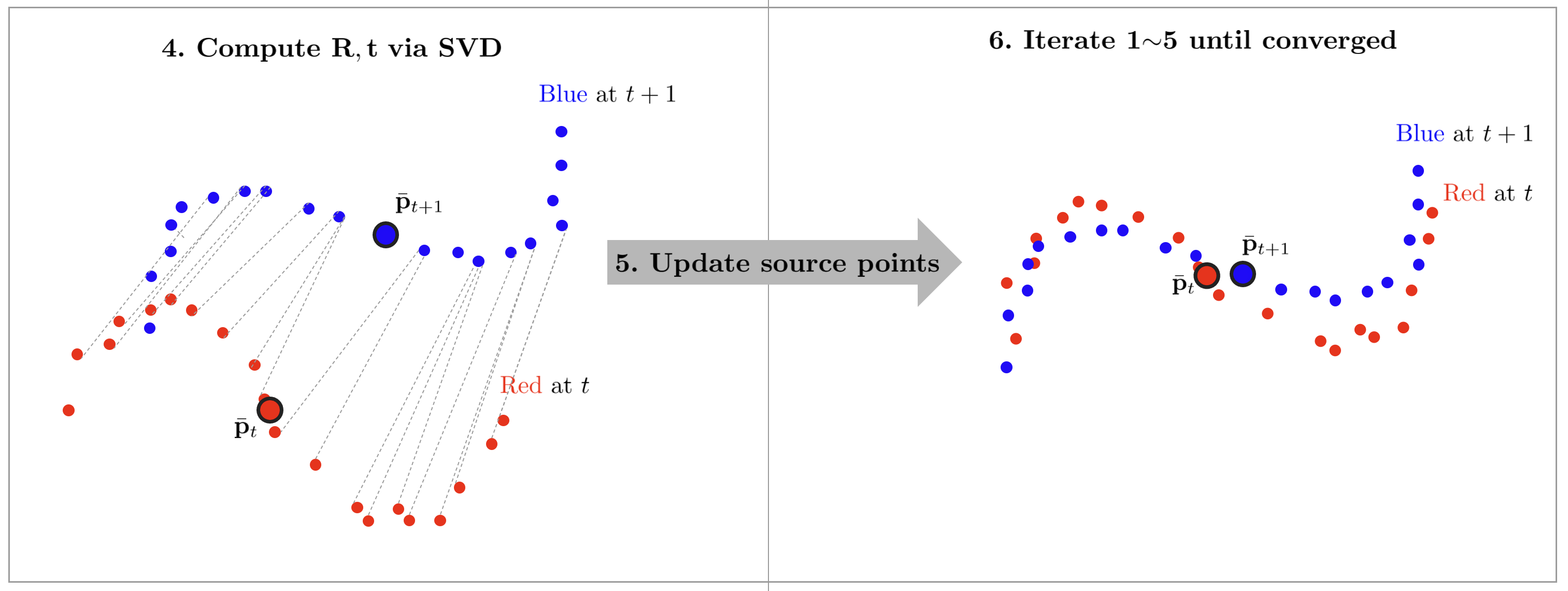
- 공분산 행렬을 SVD 분해하여 회전행렬 $\mathbf{R}$을 구하고 평균 간 차이를 통해 이동 벡터 $\mathbf{t}$를 구한다. ($\mathbf{R}_j=\mathbf{VU}^{\intercal}, \mathbf{t}_j = \bar{\mathbf{p}}_{t+1} - \mathbf{R}_j \bar{\mathbf{p}}_{t}$)
- source 점군을 최적해만큼 이동시킨다. $\mathbf{p}_{t,j+1} = \mathbf{R}_j \mathbf{p}_{t,j} + \mathbf{t}_j$
- 두 점군의 거리가 충분히 가까워질 때까지 1~5 과정을 반복한다.
ICP 과정을 그림으로 나타내면 다음과 같다.
지금까지 설명한 알고리즘을 가장 기본적인 ICP 알고리즘이라는 뜻에서 일반적으로 Vanila ICP라고 부른다. Vanila ICP는 구현하기 비교적 쉽고 초기 추정값(initial guess)가 정확하면 잘 동작한다는 장점이 있으나 일반적으로 수렴하는데 많은 반복 횟수가 필요하며 잘못된 correspondence에 영향을 많이 받아 결과가 안 좋아질 수 있는 한계점이 존재한다.
이러한 Vanila ICP의 한계점을 극복하기 위해 모든 점들이 아닌 점군의 부분 집합(e.g., 특징점)만 추출하여 ICP를 수행한다거나 point-to-plane과 같이 다른 대응 관계를 이용한다거나 correspondence에 가중치를 두어 outlier의 영향력을 축소한다거나 잠재적인 point outlier를 아예 제거하여 보다 강건한 ICP를 수행하는 등 많은 변형 ICP 방법들이 존재한다. 자세한 내용은 Cyrill 교수님의 ICP 강의 를 참고하면 된다.
Least squares point-to-point ICP (2D)
지금까지 설명했던 ICP 방법의 핵심은 두 점군의 공분산 행렬을 구한 후 SVD 분해하여 회전 행렬을 $\mathbf{R}=\mathbf{VU}^{\intercal}$과 같이 구하는 방법이었다. 이번 섹션에서는 비선형 최소제곱법(=Gauss-Newton, GN)을 사용하여 ICP 문제를 푸는 방법에 대해 설명한다. Least squares ICP는 기본적으로 대응 관계를 모르는 경우(unknown data association)에 적용할 수 있다.
Least squares ICP는 대부분 과정이 기존 ICP와 동일하지만 매 iteration마다 최적해 $\mathbf{R}, \mathbf{t}$를 추정하는 방법이 SVD -> Gauss-Newton 방법으로 변경된 점이 다르다. 또한 가장 가까운 대응점 쌍(correspondences)을 구할 때 평균을 $0$으로 설정 후 대응점 쌍을 구하지 않고 바로 대응점 쌍을 구한다는 점이 다르다.
SVD 해는 점군들의 correspondence가 point-to-point 대응점 쌍임을 가정하고 해를 구하지만 실제 ICP는 point-to-point 이외에도 다양한 에러 함수를 설정할 수 있으므로 Least squares ICP를 사용하면 이러한 에러함수를 일관되게 최적화할 수 있다. 또한 Robust estimator 같은 항을 사용하여 보다 outlier에 강건한 최적화를 수행할 수 있다.
Least squares ICP를 수행하기 위해 2차원 포즈 상태 변수 $\mathbf{x} = [t_x, t_y, \theta]^{\intercal}$를 선언한다. 2차원 회전 행렬 $\mathbf{R}$과 이동 벡터 $\mathbf{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = [t_x,t_y,\theta]^{\intercal} \\ & \mathbf{R}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \\
& \mathbf{t} = \begin{bmatrix} t_x \\ t_y \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathbf{R}(\theta)$: 회전 행렬의 입력 파라미터로 $\theta$가 들어간다는 것을 명시적으로 써준 형태이다.
최적화 식은 기존의 (\ref{eq:dataasso1})와 동일하지만 자코비안 전개의 편의를 위해 기존의 '관측값-예측값' 형태에서 '예측값-관측값' 형태로 변경해주자. $i$번째 점에 대한 에러 함수 $\mathbf{e}_i$는 다음과 같이 나타낼 수 있다.
\begin{equation} \label{eq:ls1} \begin{aligned}
\mathbf{e}_i(\mathbf{x}) = \mathbf{R}(\theta) { \mathbf{p}_{t,i}} + \mathbf{t} - {\mathbf{p}_{t+1,i}} \in \mathbb{R}^{2}
\end{aligned}
\end{equation}
\begin{equation} \boxed{ \begin{aligned}
\mathbf{x}^* & = \arg\min_{\mathbf{x}} \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& = \arg\min_{\mathbf{x}} \| \mathbf{R}(\theta) { \mathbf{p}_{t,i}} + \mathbf{t}- {\mathbf{p}_{t+1,i}} \|^2 \\
\end{aligned} }
\end{equation}
- 에러 함수가 '예측값-관측값' 형태로 변경되어도 제곱이 되므로 전체 최적화 과정에는 영향을 주지 않는다. 다만 에러 함수에 모양에 따라 자코비안의 부호가 달라지므로 실제 코드 구현 시 이에 유의한다.
위 식은 비선형 최소제곱법의 형태를 띄므로 Gauss-Newton(GN) 또는 Levenberg-Marquardt(LM) 방법으로 풀 수 있다. GN 방법을 예로 들어 설명해보자. 미소한 변화량 $\Delta \mathbf{x}$에 대하여 에러 함수 $\mathbf{e}(\mathbf{x}+\Delta \mathbf{x})$는 다음과 같이 테일러 근사를 통해 선형화할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{e}_i(\mathbf{x}+\Delta \mathbf{x}) \approx \mathbf{e}_i(\mathbf{x}) + \mathbf{J}_i\Delta \mathbf{x}
\end{aligned}
\end{equation}
$i$번째 점에 대한 자코비안 $\mathbf{J}_i$는 다음과 같다.
\begin{equation} \boxed{ \begin{aligned}
\mathbf{J}_i & = \frac{\partial \mathbf{e}_i}{\partial \mathbf{x}} \\
& = \begin{bmatrix}
\frac{\partial \mathbf{e}_i}{\partial t_x} & \frac{\partial \mathbf{e}_i}{\partial t_y} & \frac{\partial \mathbf{e}_i}{\partial \theta}
\end{bmatrix} \\
& = \begin{bmatrix}
\frac{\partial \mathbf{e}_i^{x}}{\partial t_x} & \frac{\partial \mathbf{e}_i^{x}}{\partial t_y} & \frac{\partial \mathbf{e}_i^{x}}{\partial \theta} \\
\frac{\partial \mathbf{e}_i^{y}}{\partial t_x} & \frac{\partial \mathbf{e}_i^{y}}{\partial t_y} & \frac{\partial \mathbf{e}_i^{y}}{\partial \theta}
\end{bmatrix} \\
& = \begin{bmatrix}
1 & 0 & -\sin\theta \ x_{t,i} -\cos\theta \ y_{t,i} \\
0 & 1 & \cos\theta \ x_{t,i} -\sin\theta \ y_{t,i}
\end{bmatrix} \in \mathbb{R}^{2\times 3}
\end{aligned} }
\end{equation}
위 식에서 $\theta$에 대한 자코비안 성분은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\partial \mathbf{e}_i}{\partial \theta} & = \frac{\partial}{\partial \theta} \Big( \mathbf{R}(\theta)\mathbf{p}_{t,i} \Big) \\
& = \frac{\partial}{\partial \theta} \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x_{t,i} \\ y_{t,i} \end{bmatrix} \\
& = \begin{bmatrix} -\sin\theta & -\cos\theta \\ \cos\theta & -\sin\theta \end{bmatrix} \begin{bmatrix} x_{t,i} \\ y_{t,i} \end{bmatrix} \\
& = \begin{bmatrix}
-\sin\theta \ x_{t,i} -\cos\theta \ y_{t,i} \\
\cos\theta \ x_{t,i} -\sin\theta \ y_{t,i}
\end{bmatrix} \in \mathbb{R}^{2\times 1}
\end{aligned} }
\end{equation}
- $\mathbf{p}_{t,i} = [ x_{t,i}, y_{t,i} ]^{\intercal}$
모든 점들에 대한 에러 함수를 합치면 다음과 같이 점군에 대한 에러 함수가 된다.
\begin{equation}
\begin{aligned}
& \mathbf{E}(\mathbf{x}) = \sum_i^n \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& \mathbf{x} = \arg\min_{\mathbf{x}} \mathbf{E}(\mathbf{x})
\end{aligned}
\end{equation}
점군에 대한 자코비안 $\mathbf{J}_i$와 $\mathbf{H}_i, \mathbf{b}_i$도 다음과 같이 합쳐지게 된다.
\begin{equation}
\begin{aligned}
& \mathbf{H}_i = \mathbf{J}_i^{\intercal}\mathbf{J}_i \\
& \mathbf{b}_i = \mathbf{J}_i^{\intercal}\mathbf{e}_i
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \mathbf{J} = \sum_i^n \mathbf{J}_i \\
&\mathbf{H} = \sum_i^n \mathbf{H}_i\\
& \mathbf{b} = \sum_i^n \mathbf{b}_i
\end{aligned}
\end{equation}
GN 방법의 해는 다음과 같이 구할 수 있다. 유도 과정에 대해 궁금한 독자들은 에러와 자코비안 정리 포스팅을 참고하면 된다.
\begin{equation}
\begin{aligned}
\Delta \mathbf{x}^* = - \mathbf{H}^{-1}\mathbf{b}
\end{aligned}
\end{equation}
미소 증분량의 최적해 $\Delta \mathbf{x}^*$를 위와 같이 구했으면 이를 원래 상태 변수 $\mathbf{x}$에 업데이트 해준다. 업데이트를 통해 source 점군이 target 점군에 점진적으로 정합(registration)된다.
\begin{equation}
\begin{aligned}
\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*
\end{aligned}
\end{equation}
지금까지 설명한 과정을 source 점군이 더 이상 업데이트 되지 않을 때까지 반복한다. 이러한 과정을 Least squares ICP (2D ver.) 알고리즘이라고 부른다.
Gauss-Newton method (point-to-point ICP 2D)
- Nearest neighborhood (e.g., KD-tree) 방법을 통해 source 점에 가장 가까운 target 점들을 correspondence로 설정한다.
- (\ref{eq:ls1})과 같이 에러함수를 정의한다. $\mathbf{e}(\mathbf{x})$
- 테일러 전개로 근사 선형화하여 자코비안을 구한다. $\mathbf{H} = \mathbf{J}^{\intercal}\mathbf{J}, \mathbf{b} = \mathbf{J}^{\intercal}\mathbf{e}$
- 1차 미분 후 0으로 설정한다. $\Delta \mathbf{x}^* = -\mathbf{H}^{-1}\mathbf{b}$
- 이 때 값을 구하고 이를 에러함수에 대입한다. $\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*$
- 값이 수렴할 때 까지 반복한다.
Least squares point-to-point ICP (3D)
3D 점군에 대한 Least squares ICP는 2D 점군과 비교해서 자코비안을 제외하고 모든 과정이 동일하다. 이 때, 자코비안에 3차원 회전 행렬 $\mathbf{R} \in SO(3)$이 포함되므로 자코비안을 구할 때 Lie algebra so(3)-based optimization이 적용된다는 점이 유의할만한 점이다. Lie theory-based optimization에 대한 내용은 에러와 자코비안 정리 포스팅을 참고하면 된다.
Least squares ICP를 수행하기 위해 3차원 포즈 상태 변수 $\mathbf{x} = [t_x, t_y, t_z, \mathbf{R}]^{\intercal}$를 선언한다. 3차원 회전 행렬 $\mathbf{R} \in SO(3)$과 이동 벡터 $\mathbf{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = [t_x,t_y,t_z,\mathbf{R}]^{\intercal} \\ & \mathbf{R} = \begin{bmatrix} r_{11}&r_{12}&r_{13} \\ r_{21}&r_{22}&r_{23} \\ r_{31}&r_{32}&r_{33} \end{bmatrix} \in SO(3) \\
& \mathbf{t} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}
\end{aligned}
\end{equation}
$i$번째 점에 대한 에러 함수 $\mathbf{e}_i$는 다음과 같이 나타낼 수 있다.
\begin{equation} \label{eq:ls2} \begin{aligned}
\mathbf{e}_i(\mathbf{x}) = \mathbf{R} { \mathbf{p}_{t,i}} + \mathbf{t} - {\mathbf{p}_{t+1,i}} \in \mathbb{R}^{3}
\end{aligned}
\end{equation}
\begin{equation} \boxed{ \begin{aligned}
\mathbf{x}^* & = \arg\min_{\mathbf{x}} \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& = \arg\min_{\mathbf{x}} \| \mathbf{R} { \mathbf{p}_{t,i}} + \mathbf{t}- {\mathbf{p}_{t+1,i}} \|^2 \\
\end{aligned} }
\end{equation}
위 식은 비선형 최소제곱법의 형태를 띄므로 Gauss-Newton(GN) 또는 Levenberg-Marquardt(LM) 방법으로 풀 수 있다. GN 방법을 예로 들어 설명해보자. 미소한 변화량 $\Delta \mathbf{x}$에 대하여 에러 함수 $\mathbf{e}(\mathbf{x}+\Delta \mathbf{x})$는 다음과 같이 테일러 근사를 통해 선형화할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{e}_i(\mathbf{x}+\Delta \mathbf{x}) \approx \mathbf{e}_i(\mathbf{x}) + \mathbf{J}_i\Delta \mathbf{x}
\end{aligned}
\end{equation}
$i$번째 3D 점에 대한 자코비안 $\mathbf{J}_i$은 다음과 같다.
\begin{equation}
\boxed{
\begin{aligned}
\mathbf{J}_i & = \frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial [\mathbf{t}, \mathbf{R}]} \\
& = \frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial [\mathbf{t}, \Delta \mathbf{w}]} \quad \leftarrow {\color{Mahogany} \text{so(3)-based optimization} } \\
& =\frac{\partial }{\partial [\mathbf{t}, \Delta \mathbf{w}]} \bigg( \mathbf{R}\mathbf{p}_{t,i} + \mathbf{t} - \mathbf{p}_{t+1,i} \bigg) \\
& = \begin{bmatrix} 1 & 0 & 0 & 0 & z_{t,i}’ & - y_{t,i}’
\\ 0 & 1 & 0 & -z_{t,i}’ & 0 & x_{t,i}’ \\ 0 & 0 & 1 & y_{t,i}’ & -x_{t,i}’ & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 6}
\end{aligned} }
\end{equation}
- Lie theory-based optimization에 대한 내용은 에러와 자코비안 정리 포스팅을 참고하면 된다.
$\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \mathbf{t}}$은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \mathbf{t}} & = \frac{\partial }{\partial \mathbf{t}} \mathbf{t} \\
& = \begin{bmatrix} 1 & 0 & 0
\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \in \mathbb{R}^{3 \times 3}
\end{aligned} }
\end{equation}
$\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \Delta \mathbf{w}}$은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \Delta\mathbf{w}} & = -[\mathbf{R}\mathbf{p}_{t,i}+\mathbf{t}]_{\times}\\
& = \begin{bmatrix} 0&z_{t,i}’&-y_{t,i}’ \\ -z_{t,i}’&0&x_{t,i}’ \\ y_{t,i}’ & -x_{t,i}’ & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 3}
\end{aligned} }
\end{equation}
- $\mathbf{R}\mathbf{p}_{t,i}+\mathbf{t} = [ x_{t,i}' \ y_{t,i}' \ z_{t,i}' ]^{\intercal}$
- $[\mathbf{a}]_{\times} = \begin{bmatrix}a_x\\a_y\\a_z \end{bmatrix}_{\times} = \begin{bmatrix} 0&-a_z&a_y \\ a_z&0&-a_x \\ -a_y&a_x&0 \end{bmatrix}$: 반대칭행렬 연산자
모든 점들에 대한 에러 함수를 합치면 다음과 같이 점군에 대한 에러 함수가 된다.
\begin{equation}
\begin{aligned}
& \mathbf{E}(\mathbf{x}) = \sum_i^n \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& \mathbf{x} = \arg\min_{\mathbf{x}} \mathbf{E}(\mathbf{x})
\end{aligned}
\end{equation}
점군에 대한 자코비안 $\mathbf{J}_i$와 $\mathbf{H}_i, \mathbf{b}_i$도 다음과 같이 합쳐지게 된다.
\begin{equation}
\begin{aligned}
& \mathbf{H}_i = \mathbf{J}_i^{\intercal}\mathbf{J}_i \\
& \mathbf{b}_i = \mathbf{J}_i^{\intercal}\mathbf{e}_i
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \mathbf{J} = \sum_i^n \mathbf{J}_i \\
&\mathbf{H} = \sum_i^n \mathbf{H}_i\\
& \mathbf{b} = \sum_i^n \mathbf{b}_i
\end{aligned}
\end{equation}
GN 방법의 해는 다음과 같이 구할 수 있다. 유도 과정에 대해 궁금한 독자들은 에러와 자코비안 정리 포스팅을 참고하면 된다.
\begin{equation}
\begin{aligned}
\Delta \mathbf{x}^* = - \mathbf{H}^{-1}\mathbf{b}
\end{aligned}
\end{equation}
미소 증분량의 최적해 $\Delta \mathbf{x}^*$를 위와 같이 구했으면 이를 원래 상태 변수 $\mathbf{x}$에 업데이트 해준다. 업데이트를 통해 source 점군이 target 점군에 점진적으로 정합(registration)된다.
\begin{equation}
\begin{aligned}
\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*
\end{aligned}
\end{equation}
지금까지 설명한 과정을 source 점군이 더 이상 업데이트 되지 않을 때까지 반복한다. 이러한 과정을 Least squares ICP (3D ver.) 알고리즘이라고 부른다.
Gauss-Newton method (point-to-point ICP 3D)
- Nearest neighborhood (e.g., KD-tree) 방법을 통해 source 점에 가장 가까운 target 점들을 correspondence로 설정한다.
- (\ref{eq:ls2})과 같이 에러함수를 정의한다. $\mathbf{e}(\mathbf{x})$
- 테일러 전개로 근사 선형화하여 자코비안을 구한다. $\mathbf{H} = \mathbf{J}^{\intercal}\mathbf{J}, \mathbf{b} = \mathbf{J}^{\intercal}\mathbf{e}$
- 1차 미분 후 0으로 설정한다. $\Delta \mathbf{x}^* = -\mathbf{H}^{-1}\mathbf{b}$
- 이 때 값을 구하고 이를 에러함수에 대입한다. $\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*$
- 값이 수렴할 때 까지 반복한다.
Point-to-plane ICP

기존 point-to-point ICP는 source 점과 target 점 사이의 유클리디언 거리(euclidean distance)를 최소화하는 방향으로 최적화를 수행하였다. 반면에 point-to-plane ICP는 source 점과 target 법선 벡터(normal vector) 거리를 최소화하는 방향으로 최적화를 수행한다. Point-to-plane의 원조격이 되는 논문은 [5][6][7]가 있다.
Point-to-plane 알고리즘은 point-to-point 대비 일반적으로 수렴 속도가 빠르며 노이즈와 outlier에 덜 민감하다는 특징이 있다. 반면에 법선 벡터를 계산한 후 최적화하는 과정이 추가되어 연산량이 증가한다는 trade-off 관계가 존재한다. 또한 point-to-point와 최적화 수식이 달라지므로 SVD 해를 구할 수 없고 least squares(=GN)을 통해서만 최적해를 구할 수 있다.
Least squares point-to-plane ICP (2D)
Point-to-plane ICP의 대부분의 과정은 point-to-point ICP와 동일하며 법선 벡터(normal vector)를 구하는 과정과 최적화 수식이 약간 변경되었다는 점이 다르다. Least squares ICP를 수행하기 위해 2차원 포즈 상태 변수 $\mathbf{x} = [t_x, t_y, \theta]^{\intercal}$를 선언한다. 2차원 회전 행렬 $\mathbf{R}$과 이동 벡터 $\mathbf{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = [t_x,t_y,\theta]^{\intercal} \\ & \mathbf{R}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \\
& \mathbf{t} = \begin{bmatrix} t_x \\ t_y \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathbf{R}(\theta)$: 회전 행렬의 입력 파라미터로 $\theta$가 들어간다는 것을 명시적으로 써준 형태이다.
$i$번째 점에 대한 에러 함수 $\mathbf{e}_i$는 다음과 같이 나타낼 수 있다.
\begin{equation} \label{eq:ls3} \begin{aligned}
\mathbf{e}_i(\mathbf{x}) = \mathbf{n}_{t+1,i}^{\intercal}(\mathbf{R}(\theta) { \mathbf{p}_{t,i}} + \mathbf{t} - {\mathbf{p}_{t+1,i}}) \in \mathbb{R}
\end{aligned}
\end{equation}
\begin{equation} \boxed{ \begin{aligned}
\mathbf{x}^* & = \arg\min_{\mathbf{x}} \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& = \arg\min_{\mathbf{x}} \| \mathbf{n}_{t+1,i}^{\intercal}(\mathbf{R}(\theta) { \mathbf{p}_{t,i}} + \mathbf{t}- {\mathbf{p}_{t+1,i}}) \|^2 \\
\end{aligned} }
\end{equation}
- $\mathbf{n}_{t+1,i} = [ n^x_{t+1,i} , n^y_{t+1,i} ]^{\intercal}$: target 점군에서 $i$번째 점의 법선 벡터(normal vector)
- $\mathbf{n}^{\intercal}(\cdot) = (\cdot)^{\intercal}\mathbf{n}$의 성질로 인해 법선 벡터는 식의 오른쪽과 왼쪽 어느 방향이든 위치할 수 있다.
기존 point-to-point의 최적화 수식에 법선 벡터 $\mathbf{n}_{t+1,i}$를 내적한 형태로 수식이 구성되어 있는 것을 알 수 있다. 이는 source 점과 target 점이 완벽히 정합(registration)되어 있는 경우 두 점 사이의 벡터가 법선벡터와 수직을 이루기 때문에 내적=0의 성질을 이용한 것으로 해석할 수 있다.
2D의 경우 법선 벡터는 점 $\mathbf{p} = [x,y]^{\intercal}$가 주어져 있을 때 $\mathbf{n}=[-y,x]^{\intercal}$와 같이 간단하게 구할 수 있다.
위 식은 비선형 최소제곱법의 형태를 띄므로 Gauss-Newton(GN) 또는 Levenberg-Marquardt(LM) 방법으로 풀 수 있다. GN 방법을 예로 들어 설명해보자. 미소한 변화량 $\Delta \mathbf{x}$에 대하여 에러 함수 $\mathbf{e}(\mathbf{x}+\Delta \mathbf{x})$는 다음과 같이 테일러 근사를 통해 선형화할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{e}_i(\mathbf{x}+\Delta \mathbf{x}) \approx \mathbf{e}_i(\mathbf{x}) + \mathbf{J}_i\Delta \mathbf{x}
\end{aligned}
\end{equation}
$i$번째 점에 대한 자코비안 $\mathbf{J}_i$는 다음과 같다.
\begin{equation} \boxed{ \begin{aligned}
\mathbf{J}_i & = \frac{\partial \mathbf{e}_i}{\partial \mathbf{x}} \\
& = \begin{bmatrix}
\frac{\partial \mathbf{e}_i}{\partial t_x} & \frac{\partial \mathbf{e}_i}{\partial t_y} & \frac{\partial \mathbf{e}_i}{\partial \theta}
\end{bmatrix} \\
& = \begin{bmatrix}
\frac{\partial \mathbf{e}_i^{x}}{\partial t_x} & \frac{\partial \mathbf{e}_i^{x}}{\partial t_y} & \frac{\partial \mathbf{e}_i^{x}}{\partial \theta} \\
\frac{\partial \mathbf{e}_i^{y}}{\partial t_x} & \frac{\partial \mathbf{e}_i^{y}}{\partial t_y} & \frac{\partial \mathbf{e}_i^{y}}{\partial \theta}
\end{bmatrix} \\
& = \begin{bmatrix}
n^x_{t+1,i} & n^y_{t+1,i} & n^x_{t+1,i}(-\sin\theta \ x_{t,i} -\cos\theta \ y_{t,i}) + n^y_{t+1,i}(\cos\theta \ x_{t,i} -\sin\theta \ y_{t,i})
\end{bmatrix} \in \mathbb{R}^{1\times 3}
\end{aligned} }
\end{equation}
위 식에서 $\theta$에 대한 자코비안 성분은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\partial \mathbf{e}_i}{\partial \theta} & = \frac{\partial}{\partial \theta} \Big( \mathbf{n}_{t+1,i}^{\intercal} \mathbf{R}(\theta)\mathbf{p}_{t,i} \Big) \\
& = \frac{\partial}{\partial \theta} \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} \end{bmatrix} \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x_{t,i} \\ y_{t,i} \end{bmatrix} \\
& = \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} \end{bmatrix} \begin{bmatrix} -\sin\theta & -\cos\theta \\ \cos\theta & -\sin\theta \end{bmatrix} \begin{bmatrix} x_{t,i} \\ y_{t,i} \end{bmatrix} \\
& = \begin{bmatrix}
n^x_{t+1,i}(-\sin\theta \ x_{t,i} -\cos\theta \ y_{t,i}) - n^y_{t+1,i}(\cos\theta \ x_{t,i} -\sin\theta \ y_{t,i})
\end{bmatrix} \in \mathbb{R}
\end{aligned} }
\end{equation}
- $\mathbf{p}_{t,i} = [ x_{t,i}, y_{t,i} ]^{\intercal}$
- $\mathbf{n}_{t+1,i} = [ n^x_{t+1,i}, n^y_{t+1,i} ]^{\intercal}$
모든 점들에 대한 에러 함수를 합치면 다음과 같이 점군에 대한 에러 함수가 된다.
\begin{equation}
\begin{aligned}
& \mathbf{E}(\mathbf{x}) = \sum_i^n \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& \mathbf{x} = \arg\min_{\mathbf{x}} \mathbf{E}(\mathbf{x})
\end{aligned}
\end{equation}
점군에 대한 자코비안 $\mathbf{J}_i$와 $\mathbf{H}_i, \mathbf{b}_i$도 다음과 같이 합쳐지게 된다.
\begin{equation}
\begin{aligned}
& \mathbf{H}_i = \mathbf{J}_i^{\intercal}\mathbf{J}_i \\
& \mathbf{b}_i = \mathbf{J}_i^{\intercal}\mathbf{e}_i
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \mathbf{J} = \sum_i^n \mathbf{J}_i \\
&\mathbf{H} = \sum_i^n \mathbf{H}_i\\
& \mathbf{b} = \sum_i^n \mathbf{b}_i
\end{aligned}
\end{equation}
GN 방법의 해는 다음과 같이 구할 수 있다. 유도 과정에 대해 궁금한 독자들은 에러와 자코비안 정리 포스팅을 참고하면 된다.
\begin{equation}
\begin{aligned}
\Delta \mathbf{x}^* = - \mathbf{H}^{-1}\mathbf{b}
\end{aligned}
\end{equation}
미소 증분량의 최적해 $\Delta \mathbf{x}^*$를 위와 같이 구했으면 이를 원래 상태 변수 $\mathbf{x}$에 업데이트 해준다. 업데이트를 통해 source 점군이 target 점군에 점진적으로 정합(registration)된다.
\begin{equation}
\begin{aligned}
\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*
\end{aligned}
\end{equation}
지금까지 설명한 과정을 source 점군이 더 이상 업데이트 되지 않을 때까지 반복한다. 이러한 과정을 Least squares ICP (2D ver.) 알고리즘이라고 부른다.
Gauss-Newton method (point-to-plane ICP 2D)
- Nearest neighborhood (e.g., KD-tree) 방법을 통해 source 점에 가장 가까운 target 점들을 correspondence로 설정한다.
- target 점들의 법선 벡터(normal vector) $\mathbf{n}$을 계산한다. (2D: $\mathbf{p}=[x,y]^{\intercal}, \mathbf{n}=[-y,x]^{\intercal}$)
- (\ref{eq:ls3})과 같이 에러함수를 정의한다. $\mathbf{e}(\mathbf{x})$
- 테일러 전개로 근사 선형화하여 자코비안을 구한다. $\mathbf{H} = \mathbf{J}^{\intercal}\mathbf{J}, \mathbf{b} = \mathbf{J}^{\intercal}\mathbf{e}$
- 1차 미분 후 0으로 설정한다. $\Delta \mathbf{x}^* = -\mathbf{H}^{-1}\mathbf{b}$
- 이 때 값을 구하고 이를 에러함수에 대입한다. $\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*$
- 값이 수렴할 때 까지 반복한다.
Least squares point-to-plane ICP (3D)
3D 역시 point-to-plane ICP의 대부분의 과정은 point-to-point ICP와 동일하며 법선 벡터(normal vector)를 구하는 과정과 최적화 수식이 약간 변경되었다는 점이 다르다. Least squares ICP를 수행하기 위해 3차원 포즈 상태 변수 $\mathbf{x} = [t_x, t_y, t_z, \mathbf{R}]^{\intercal}$를 선언한다. 3차원 회전 행렬 $\mathbf{R} \in SO(3)$과 이동 벡터 $\mathbf{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = [t_x,t_y,t_z,\mathbf{R}]^{\intercal} \\ & \mathbf{R} = \begin{bmatrix} r_{11}&r_{12}&r_{13} \\ r_{21}&r_{22}&r_{23} \\ r_{31}&r_{32}&r_{33} \end{bmatrix} \in SO(3) \\
& \mathbf{t} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}
\end{aligned}
\end{equation}
$i$번째 점에 대한 에러 함수 $\mathbf{e}_i$는 다음과 같이 나타낼 수 있다.
\begin{equation} \label{eq:ls4} \begin{aligned}
\mathbf{e}_i(\mathbf{x}) = \mathbf{n}_{t+1,i}^{\intercal} ( \mathbf{R} { \mathbf{p}_{t,i}} + \mathbf{t} - {\mathbf{p}_{t+1,i}}) \in \mathbb{R}
\end{aligned}
\end{equation}
\begin{equation} \boxed{ \begin{aligned}
\mathbf{x}^* & = \arg\min_{\mathbf{x}} \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& = \arg\min_{\mathbf{x}} \| \mathbf{n}_{t+1,i}^{\intercal}(\mathbf{R} { \mathbf{p}_{t,i}} + \mathbf{t}- {\mathbf{p}_{t+1,i}} ) \|^2 \\
\end{aligned} }
\end{equation}
- $\mathbf{n}_{t+1,i} = [ n^x_{t+1,i} , n^y_{t+1,i}, n^z_{t+1,i} ]^{\intercal}$: target 점군에서 $i$번째 점의 법선 벡터(normal vector)
- $\mathbf{n}^{\intercal}(\cdot) = (\cdot)^{\intercal}\mathbf{n}$의 성질로 인해 법선 벡터는 식의 오른쪽과 왼쪽 어느 방향이든 위치할 수 있다.
기존 point-to-point의 최적화 수식에 법선 벡터 $\mathbf{n}_{t+1,i}$를 내적한 형태로 수식이 구성되어 있는 것을 알 수 있다. 이는 source 점과 target 점이 완벽히 정합(registration)되어 있는 경우 두 점 사이의 벡터가 법선벡터와 수직을 이루기 때문에 내적=0의 성질을 이용한 것으로 해석할 수 있다.
법선 벡터는 다양한 방법을 통해 구할 수 있는데 3D의 경우 점 $\mathbf{p} = [x,y,z]^{\intercal}$가 주어져 있을 때 $\mathbf{p}$로부터 가장 가까운 점 2개 $\mathbf{p}_{1}, \mathbf{p}_{2}$를 nearest neighbor(e.g., KD-tree)를 통해 구한 후 두 점을 외적하여 $\mathbf{n} = \mathbf{p}_{1} \times \mathbf{p}_2$를 구할 수 있다. 또한 주변의 $k$개의 점을 구한 다음 PCA를 통해 가장 작은 고유값(eigenvalue)에 대응하는 고유 벡터(eigenvector)가 법선벡터인 성질을 이용하여 구할 수 있다.
위 식은 비선형 최소제곱법의 형태를 띄므로 Gauss-Newton(GN) 또는 Levenberg-Marquardt(LM) 방법으로 풀 수 있다. GN 방법을 예로 들어 설명해보자. 미소한 변화량 $\Delta \mathbf{x}$에 대하여 에러 함수 $\mathbf{e}(\mathbf{x}+\Delta \mathbf{x})$는 다음과 같이 테일러 근사를 통해 선형화할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{e}_i(\mathbf{x}+\Delta \mathbf{x}) \approx \mathbf{e}_i(\mathbf{x}) + \mathbf{J}_i\Delta \mathbf{x}
\end{aligned}
\end{equation}
$i$번째 3D 점에 대한 자코비안 $\mathbf{J}_i$은 다음과 같다.
\begin{equation}
\boxed{
\begin{aligned}
\mathbf{J}_i & = \frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial [\mathbf{t}, \mathbf{R}]} \\
& = \frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial [\mathbf{t}, \Delta \mathbf{w}]} \quad \leftarrow {\color{Mahogany} \text{so(3)-based optimization} } \\
& =\frac{\partial }{\partial [\mathbf{t}, \Delta \mathbf{w}]} \bigg( \mathbf{n}_{t+1,i}^{\intercal}( \mathbf{R}\mathbf{p}_{t,i} + \mathbf{t} - \mathbf{p}_{t+1,i} ) \bigg) \\
& = \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} & n^z_{t+1,i} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & 0 & z_{t,i}’ & - y_{t,i}’
\\ 0 & 1 & 0 & -z_{t,i}’ & 0 & x_{t,i}’ \\ 0 & 0 & 1 & y_{t,i}’ & -x_{t,i}’ & 0 \end{bmatrix} \\ & = \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} & n^z_{t+1,i} & n^x_{t+1,i}(-z'_{t,i}+y'_{t,i}) & n^y_{t+1,i}(z'_{t,i} - x'_{t,i}) & n^z_{t+1,i}(-y'_{t,i} + x'_{t,i}) \end{bmatrix} \in \mathbb{R}^{1 \times 6}
\end{aligned} }
\end{equation}
- Lie theory-based optimization에 대한 내용은 에러와 자코비안 정리 포스팅을 참고하면 된다.
$\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \mathbf{t}}$은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \mathbf{t}} & = \frac{\partial }{\partial \mathbf{t}} \mathbf{n}_{t+1,i}^{\intercal} \mathbf{t} \\
& = \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} & n^z_{t+1,i} \end{bmatrix}\begin{bmatrix} 1 & 0 & 0
\\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \\ & = \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} & n^z_{t+1,i} \end{bmatrix} \in \mathbb{R}^{1\times 3}
\end{aligned} }
\end{equation}
$\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \Delta \mathbf{w}}$은 다음과 같다.
\begin{equation}
\boxed{ \begin{aligned}
\frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial \Delta\mathbf{w}} & = -\mathbf{n}_{t+1,i}^{\intercal}[\mathbf{R}\mathbf{p}_{t,i}+\mathbf{t}]_{\times}\\
& = \begin{bmatrix} n^x_{t+1,i} & n^y_{t+1,i} & n^z_{t+1,i} \end{bmatrix} \begin{bmatrix} 0&z_{t,i}’&-y_{t,i}’ \\ -z_{t,i}’&0&x_{t,i}’ \\ y_{t,i}’ & -x_{t,i}’ & 0 \end{bmatrix} \\ & = \begin{bmatrix} n^x_{t+1,i}(-z'_{t,i} + y'_{t,i}) & n^y_{t+1,i}(z'_{t,i} - x'_{t,i}) & n^z_{t+1,i}(-y'_{t,i} + x'_{t,i}) \end{bmatrix} \in \mathbb{R}^{1 \times 3}
\end{aligned} }
\end{equation}
- $\mathbf{R}\mathbf{p}_{t,i}+\mathbf{t} = [ x_{t,i}' \ y_{t,i}' \ z_{t,i}' ]^{\intercal}$
- $[\mathbf{a}]_{\times} = \begin{bmatrix}a_x\\a_y\\a_z \end{bmatrix}_{\times} = \begin{bmatrix} 0&-a_z&a_y \\ a_z&0&-a_x \\ -a_y&a_x&0 \end{bmatrix}$: 반대칭행렬 연산자
모든 점들에 대한 에러 함수를 합치면 다음과 같이 점군에 대한 에러 함수가 된다.
\begin{equation}
\begin{aligned}
& \mathbf{E}(\mathbf{x}) = \sum_i^n \| \mathbf{e}_i(\mathbf{x}) \|^2 \\
& \mathbf{x} = \arg\min_{\mathbf{x}} \mathbf{E}(\mathbf{x})
\end{aligned}
\end{equation}
점군에 대한 자코비안 $\mathbf{J}_i$와 $\mathbf{H}_i, \mathbf{b}_i$도 다음과 같이 합쳐지게 된다.
\begin{equation}
\begin{aligned}
& \mathbf{H}_i = \mathbf{J}_i^{\intercal}\mathbf{J}_i \\
& \mathbf{b}_i = \mathbf{J}_i^{\intercal}\mathbf{e}_i
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \mathbf{J} = \sum_i^n \mathbf{J}_i \\
&\mathbf{H} = \sum_i^n \mathbf{H}_i\\
& \mathbf{b} = \sum_i^n \mathbf{b}_i
\end{aligned}
\end{equation}
GN 방법의 해는 다음과 같이 구할 수 있다. 유도 과정에 대해 궁금한 독자들은 에러와 자코비안 정리 포스팅을 참고하면 된다.
\begin{equation}
\begin{aligned}
\Delta \mathbf{x}^* = - \mathbf{H}^{-1}\mathbf{b}
\end{aligned}
\end{equation}
미소 증분량의 최적해 $\Delta \mathbf{x}^*$를 위와 같이 구했으면 이를 원래 상태 변수 $\mathbf{x}$에 업데이트 해준다. 업데이트를 통해 source 점군이 target 점군에 점진적으로 정합(registration)된다.
\begin{equation}
\begin{aligned}
\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*
\end{aligned}
\end{equation}
지금까지 설명한 과정을 source 점군이 더 이상 업데이트 되지 않을 때까지 반복한다. 이러한 과정을 Least squares ICP (3D ver.) 알고리즘이라고 부른다.
Gauss-Newton method (point-to-plane ICP 3D)
- Nearest neighborhood (e.g., KD-tree) 방법을 통해 source 점에 가장 가까운 target 점들을 correspondence로 설정한다.
- target 점들의 법선 벡터(normal vector) $\mathbf{n}$을 계산한다.
- (\ref{eq:ls4})과 같이 에러함수를 정의한다. $\mathbf{e}(\mathbf{x})$
- 테일러 전개로 근사 선형화하여 자코비안을 구한다. $\mathbf{H} = \mathbf{J}^{\intercal}\mathbf{J}, \mathbf{b} = \mathbf{J}^{\intercal}\mathbf{e}$
- 1차 미분 후 0으로 설정한다. $\Delta \mathbf{x}^* = -\mathbf{H}^{-1}\mathbf{b}$
- 이 때 값을 구하고 이를 에러함수에 대입한다. $\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*$
- 값이 수렴할 때 까지 반복한다.
Generalized-ICP (GICP)
Generalized-ICP(GICP)는 기존 ICP 알고리즘들과 달리 점을 확률 기반으로 모델링하여 점군 간 변환을 추정하는 알고리즘이다. GICP는 공분산 행렬의 형태에 따라 point-to-point, point-to-plane, plane-to-plane ICP 방법을 모두 포함할 수 있다. 이러한 이유로 인해 일반화된(generalized) ICP라는 이름이 붙여진 것으로 보인다. 하지만 가장 가까운 대응점 쌍(correspondence)를 구할 때는 여전히 확률 기반이 아닌 거리 기반(nearest neighbor, KD-tree)을 사용하여 KNN 알고리즘의 속도는 유지하였다.
GICP[8]는 대응점 쌍이 구해졌다고 가정한 상태에서 수식을 유도한다. Source 점군이 ${\mathbf{p}_{t}} = [\mathbf{p}_{t,1}, \mathbf{p}_{t,2}, \cdots, \mathbf{p}_{t,n}]^{\intercal}$이고 target 점군이 ${\mathbf{p}_{t+1}} = [\mathbf{p}_{t+1,1}, \mathbf{p}_{t+1,2}, \cdots, \mathbf{p}_{t+1,n}]^{\intercal}$와 같이 주어져 있을 때 각각의 점들이 가우시안 확률 분포를 따르고 있다고 모델링한다.
\begin{equation}
\begin{aligned}
& \mathbf{p}_{t,i} \sim \mathcal{N}(\hat{\mathbf{p}}_{t,i}, \mathbf{C}_{t,i}) \\
& \mathbf{p}_{t+1,i} \sim \mathcal{N}(\hat{\mathbf{p}}_{t+1,i}, \mathbf{C}_{t+1,i}) \\
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \hat{\mathbf{p}}_{t} = [ \hat{\mathbf{p}}_{t,1}, \hat{\mathbf{p}}_{t,2}, \cdots, \hat{\mathbf{p}}_{t,n} ]^{\intercal} \\
& \hat{\mathbf{p}}_{t+1} = [ \hat{\mathbf{p}}_{t+1,1}, \hat{\mathbf{p}}_{t+1,2}, \cdots, \hat{\mathbf{p}}_{t+1,n} ]^{\intercal}\end{aligned}
\end{equation}
만약 두 점군이 노이즈 또는 outlier 없이 정확히 유클리디언 거리만큼 떨어져 있는 경우 두 점 사이에는 다음과 같은 변환 관계가 성립한다.
\begin{equation}
\begin{aligned}
\hat{\mathbf{p}}_{t+1,i} & = \mathbf{T}^*\hat{\mathbf{p}}_{t,i}
\end{aligned}
\end{equation}
두 점 사이의 임의의 변환 $\mathbf{T}$에 대하여
\begin{equation}
\boxed{ \begin{aligned}
d_i = \hat{\mathbf{p}}_{t+1,i} - \mathbf{T}\hat{\mathbf{p}}_{t,i}
\end{aligned} }
\end{equation}
와 같이 거리 함수 $d_i$를 정의할 수 있다. 이 때, $\hat{\mathbf{p}}_{t,i}, \hat{\mathbf{p}}_{t+1,i}$ 모두 확률 변수(random variable)이므로 $d_i$ 또한 확률 분포를 따른다.
\begin{equation}
\begin{aligned}
d_i \vert_{\mathbf{T}=\mathbf{T}^*} & \sim \mathcal{N}({\color{Mahogany} \hat{\mathbf{p}}_{t+1,i} - \mathbf{T}^*\hat{\mathbf{p}}_{t,i} }, \mathbf{C}_{t+1,i} + \mathbf{T}^* \mathbf{C}_{t,i} \mathbf{T}^{*\intercal}) \\
& = \mathcal{N}({\color{Mahogany} \mathbf{0} }, \mathbf{C}_{t+1,i} + \mathbf{T}^* \mathbf{C}_{t,i} \mathbf{T}^{*\intercal})
\end{aligned}
\end{equation}
- 두 점 $\hat{\mathbf{p}}_{t,i}, \hat{\mathbf{p}}_{t+1,i}$은 서로 독립적인(independent) 가우시안 분포를 따른다고 가정한다.
Linear transformation of gaussian random variable
확률 변수 $\mathbf{x}$가 $\mathbf{x} \sim \mathcal{N}(\mathbf{a}, \mathbf{B})$와 같이 평균이 $\mathbf{a}$이고 공분산이 $\mathbf{B}$인 가우시안 분포를 따른다고 했을 때, 임의의 행렬 $\mathbf{C}$에 대하여 $\mathbf{y} = \mathbf{C}\mathbf{x}$를 만족하는 $\mathbf{y}$ 또한 확률 변수이고 $\mathbf{y} \sim \mathcal{N}(\mathbf{Ca}, \mathbf{CBC}^{\intercal})$인 가우시안 분포를 따른다.
보다 자세한 내용은 확률 이론 포스팅을 참조하면 된다.
위 식은 $i$번째 source, target 점들의 거리에 대한 함수이므로 이를 모든 점군에 대하여 합하여 $d_i$에 대한 pdf $p(d_i)$를 모두 곱하면 다음과 같은 $\mathbf{T}$에 대한 maximum likelihood esitmation(MLE) 최적화 공식이 구해진다.
\begin{equation} \label{eq:gicp1}
\boxed{ \begin{aligned}
\mathbf{T} & = \arg\max_{\mathbf{T}} \Pi_i p(d_i) \quad \leftarrow {\color{Mahogany} \text{likelihood} } \\
& = \arg\max_{\mathbf{T}} \sum_i \log p(d_i) \quad \leftarrow {\color{Mahogany} \text{log-likelihood} }
\end{aligned} }
\end{equation}
$p(d_i)$는 다음과 같다. $p(d_i)$의 평균은 $d_i \vert_{\mathbf{T}=\mathbf{T}^*}=0$처럼 0이 되어 생략되었다.
\begin{equation}
\begin{aligned}
p(d_i) & = \eta \cdot \exp \bigg( -\frac{1}{2} d_i^{\intercal} (\mathbf{C}_{t+1,i} + \mathbf{T}\mathbf{C}_{t,i}\mathbf{T}^{\intercal})^{-1} d_i \bigg) \\
& \sim \mathcal{N}({\color{Mahogany} \mathbf{0} }, \mathbf{C}_{t+1,i} + \mathbf{TC}_{t,i}\mathbf{T}^{\intercal})
\end{aligned}
\end{equation}
따라서 (\ref{eq:gicp1})은 다음과 같이 쓸 수 있다. 위 식의 log-likelihood에서 $(-)$ 부호를 제거하고 나머지 식만 고려하여 argmax가 argmin으로 변경되었다(=$\color{Mahogany}\text{negative log-likelihood}$) .
\begin{equation} \label{eq:gicp2}
\boxed{ \begin{aligned}
\mathbf{T} & = \arg\min_{\mathbf{T}} \sum_i d_i^{\intercal} (\mathbf{C}_{t+1,i} + \mathbf{T}\mathbf{C}_{t,i}\mathbf{T}^{\intercal})^{-1} d_i
\end{aligned} }
\end{equation}
Point-to-point ICP in GICP
GICP가 일반화된(generalized) ICP로 불리는 이유는 (\ref{eq:gicp2}) 수식에서 공분산 행렬 $\mathbf{C}_{t,i}, \mathbf{C}_{t+1,i}$ 값을 변형함으로써 point-to-point, point-to-plane, plane-to-plane ICP의 수식이 모두 도출되기 때문이다.
만약 공분산 행렬이 다음과 같은 경우 point-to-point ICP 수식이 유도된다.
\begin{equation}
\begin{aligned}
& \mathbf{C}_{t+1,i} = \mathbf{I} \\
& \mathbf{C}_{t,i} = \mathbf{0}
\end{aligned}
\end{equation}
위 식을 (\ref{eq:gicp2})에 대입하면 다음과 같은 식이 도출된다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{T} & = \arg\min_{\mathbf{T}} \sum_i d_i^{\intercal} d_i \\
& = \arg\min_{\mathbf{T}} \sum_i \| d_i \|^2
\end{aligned} }
\end{equation}
이는 point-to-point ICP의 수식과 정확히 일치한다.
Point-to-plane ICP in GICP
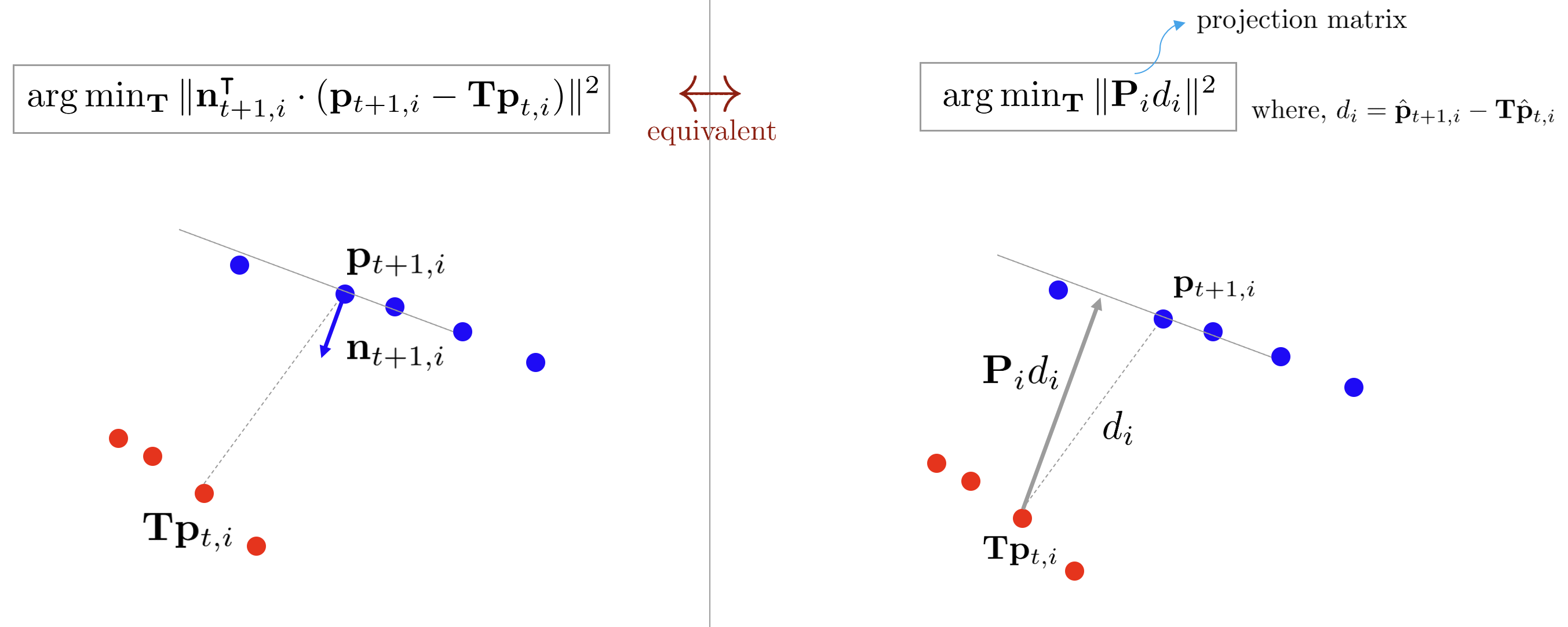
앞서 설명한 point-to-plane ICP는 source 점과 target 평면 사이의 거리를 최소화하는 알고리즘이었다. 따라서 target 평면의 법선 벡터 $\mathbf{n}_i$를 기존 수식에 내적하는 식으로 최적화 수식이 구성되었다. GICP에서는 관점을 약간 다르게하여 두 점 사이의 거리 벡터 $d_i$에 target 평면 방향으로 프로젝션한 투영 행렬 $\mathbf{P}_i$를 곱한 식을 최적화하는 방식으로 해석한다.
\begin{equation} \label{eq:gicp3}
\begin{aligned}
\mathbf{T} & = \arg\min_{\mathbf{T}} \sum_i \| \mathbf{P}_i d_i \|^2
\end{aligned}
\end{equation}
위 식에서 $\mathbf{P}_i$는 source 점으로부터 target 평면의 법선 방향에 대한 프로젝션한 투영 행렬을 의미한다. 투영 행렬의 성질에 따라 $\mathbf{P}_i = \mathbf{P}_i^2 = \mathbf{P}_i^{\intercal}$이 성립한다. 따라서 위 식은 다음과 같이 변형될 수 있다.
\begin{equation}
\begin{aligned}
\| \mathbf{P}_i d_i \|^2 & = (\mathbf{P}_i d_i)^{\intercal} (\mathbf{P}_i d_i) \\
& = d_i^{\intercal} \mathbf{P}_i d_i
\end{aligned}
\end{equation}
이에 따라 (\ref{eq:gicp3}) 수식은 다음과 같이 쓸 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{T} & = \arg\min_{\mathbf{T}} \sum_i \| \mathbf{P}_i d_i\|^2 \\
& = \arg\min_{\mathbf{T}} \sum_i \| d_i^{\intercal}\mathbf{P}_i d_i \|^2
\end{aligned} }
\end{equation}
이는 GICP 수식 (\ref{eq:gicp2})에서 공분산 행렬이 다음과 같은 경우에 해당한다.
\begin{equation} \label{eq:gicp4}
\begin{aligned}
& \mathbf{C}_{t+1,i} = \mathbf{P}_i^{-1} \\
& \mathbf{C}_{t,i} = \mathbf{0}
\end{aligned}
\end{equation}
엄밀하게 말하면 투영 행렬 $\mathbf{P}_i$는 rank deficient이기 때문에 full rank가 아니므로 역행렬이 존재하지 않는다. 그러나 $\mathbf{P}_i$를 역행렬이 존재하는 $\mathbf{Q}_i$로 근사화할 수는 있다. $\mathbf{Q}_i$는 $\mathbf{P}_i$와 비슷하지만 full rank인 역행렬이 존재하는 행렬로 가정한다. 따라서 GICP 식에서 $\mathbf{Q}_i$가 $\mathbf{P}_i$에 가까울수록 GICP는 point-to-plane ICP로 수렴하게 된다.
Projection Matrix $\mathbf{P}$
투영 행렬 $\mathbf{P}_i$가 rank deficient인 이유는 고차원 벡터 공간의 점(또는 벡터)를 저차원 부분 공간으로 투영(projection)하는 역할을 하기 때문이다. Point-to-plane 예시에서는 source 점 $\mathbf{T}\mathbf{p}_{t,i}$가 target 점 $\mathbf{p}_{t+1,i}$가 이루는 평면의 부분 공간으로 투영(projection)되는 것으로 해석할 수 있다. 투영 행렬에 대한 자세한 설명은 선형대수학 개념 정리 포스팅을 참조하면 된다.
Plane-to-plane ICP in GICP
마지막으로 GICP는 source 평면과 target 평면 사이의 거리를 최소화하는 plane-to-plane ICP 또한 수행할 수 있다. 이는 단순히 (\ref{eq:gicp4}) 식에서 $\mathbf{C}_{t,i}$를 $\mathbf{0}$이 아닌 프로젝션 행렬 $\mathbf{P}_i^{'-1}$로 나타내면 된다고 생각할 수 있으나 그렇게 되면 두 투영 행렬들 $\mathbf{P}_i, \mathbf{P}'_i$이 rank deficient하여 singular한 값을 가지므로 이를 근사화한다고 해도 높은 정확도를 기대하기는 힘들다.
이에 따라 여러 가정을 통해 plane에 대한 공분산 행렬을 모델링한다.
- 스캔 데이터는 실제 3차원 공간의 부드러운 다양체(2-manifold)를 샘플링 한 것이므로 모든 포인트에서 미분 가능하다(=법선 벡터를 구할 수 있다).
- 서로 다른 시점(t,t+1)에서 샘플링한 데이터는 일반적으러 정확히 같은 점을 샘플링하지 않는다. 따라서 가장 가까운 대응점 쌍(nearest correspondence)는 0이 될 수 없다.
- 샘플링된 점은 평면의 수평한 방향으로 높은 공분산을 가지고 수직한(법선벡터) 방향으로는 낮은 공분산을 가진다고 간주한다.
만약 $x$축으로 법선 벡터를 갖는 경우 위 가정에 따라 공분산 $\mathbf{C}_x$은 다음과 같이 모델링할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{C}_x = \begin{bmatrix}
\epsilon && \\ &1& \\ &&1
\end{bmatrix}
\end{aligned}
\end{equation}
- $\epsilon$: 법선 방향으로 공분산을 나타내는 작은 상수값 ($\epsilon \ll 1$)

$i$번째 source 점 $\mathbf{p}_{t,i}$와 target 점 $\mathbf{p}_{t+1,i}$의 법선 벡터를 각각 $\mu_i$와 $\nu_i$라고 하면 plane-to-plane의 공분산 행렬은 다음과 같이 나타낼 수 있다.
\begin{equation} \begin{aligned}
& \mathbf{C}_{t,i} = \mathbf{R}_{\mu_i}
\begin{bmatrix}
\epsilon && \\ &1& \\ &&1
\end{bmatrix} \mathbf{R}_{\mu_i}^{\intercal} \\
& \mathbf{C}_{t+1,i} = \mathbf{R}_{\nu_i}
\begin{bmatrix}
\epsilon && \\ &1& \\ &&1
\end{bmatrix} \mathbf{R}_{\nu_i}^{\intercal} \\
\end{aligned}
\end{equation}
- $\mathbf{R}_{\mu_i}$: $x$축의 방향 벡터를 $\mu_i$로 회전해주는 행렬
- $\mathbf{R}_{\nu_i}$: $x$축의 방향 벡터를 $\nu_i$로 회전해주는 행렬
위 식을 (\ref{eq:gicp2})에 대입함으로써 plane-to-plane ICP를 수행할 수 있다. Plane-to-plane ICP는 법선 벡터의 방향이 다른 두 점이 대응점 쌍으로 주어진 경우 최종 합산된 공분산 행렬이 등방성을 가지게 되어 최적화 수식 기여하는 정도가 매우 작아진다. 즉, outlier에 강건한 특성을 지닌다. 다만 모든 스캔 점들에 대한 법선 벡터를 계산해야 하므로 연산량이 많다는 특징이 있다.
법선 벡터를 추정하는 방법은 다양하게 있으며 GICP 논문에서는 각 스캔한 점에 대해 가장 가까운 주변의 20개의 점을 KD-Tree를 통해 구한 후 공분산 행렬에 PCA를 사용하여 법선 벡터를 계산하였다. 이 때, 가장 작은 고유값(eigenvalue)에 해당하는 고유 벡터(eigenvector)가 법선 벡터에 해당한다.
Least squares GICP (3D)
GICP는 (\ref{eq:gicp2}) 수식을 비선형 최소제곱법(GN, LM)을 반복적으로 최적해를 구한다. 앞서 설명한 point-to-point, point-to-plane ICP와 비교했을 때 확률 기반 모델링으로 인한 공분산이 최적화 수식에 추가된다는 점을 제외하곤 거의 모든 과정이 동일하다. Least squares GICP를 수행하기 위해 3차원 포즈 상태 변수 $\mathbf{x} = [t_x, t_y, t_z, \mathbf{R}]^{\intercal}$를 선언한다. 3차원 회전 행렬 $\mathbf{R} \in SO(3)$과 이동 벡터 $\mathbf{t}$는 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = [t_x,t_y,t_z,\mathbf{R}]^{\intercal} \\ & \mathbf{R} = \begin{bmatrix} r_{11}&r_{12}&r_{13} \\ r_{21}&r_{22}&r_{23} \\ r_{31}&r_{32}&r_{33} \end{bmatrix} \in SO(3) \\
& \mathbf{t} = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix}
\end{aligned}
\end{equation}
$i$번째 점에 대한 에러 함수 $\mathbf{e}_i$는 다음과 같이 나타낼 수 있다.
\begin{equation} \begin{aligned}
\mathbf{e}_i(\mathbf{x}) = (\hat{\mathbf{p}}_{t+1,i} - \mathbf{R}\hat{\mathbf{p}}_{t,i} - \mathbf{t})
\end{aligned}
\end{equation}
\begin{equation} \boxed{ \begin{aligned}
\mathbf{x}^* & = \arg\min_{\mathbf{x}} \| \mathbf{e}_i(\mathbf{x}) \|_{\mathbf{M}^{-1}}^2 \\
& = \arg\min_{\mathbf{x}} \|
(\hat{\mathbf{p}}_{t+1,i} - \mathbf{R}\hat{\mathbf{p}}_{t,i} - \mathbf{t})
\|_{\mathbf{M}^{-1}}^2 \\
\end{aligned} }
\end{equation}
- $d_i = \hat{\mathbf{p}}_{t+1,i} - \mathbf{R}\hat{\mathbf{p}}_{t,i} - \mathbf{t}$: 위 식에는 $d_i$를 풀어서 작성하였다.
- $\| \mathbf{a} \|_{\mathbf{B}}^{2} = \mathbf{a}^{\intercal} \mathbf{B}^{-1} \mathbf{a}$: 마할라노비스 놈(Mahalanobis norm)
- $\mathbf{M} = (\mathbf{C}_{t+1,i} + \mathbf{R}\mathbf{C}_{t,i}\mathbf{R}^{\intercal})^{-1}$: 공분산의 역행렬
- $\mathbf{M}^{-1}$: 공분산 행렬
기존 ICP들과 달리 GICP는 확률 기반으로 모델링하기였기 때문에 mahalanobis norm $\| \cdot \|^2_{\mathbf{M}^{-1}}$을 최적화해야 한다. (\ref{eq:gicp2})에서 수식을 유도할 때는 $\mathbf{T} \in SE(3)$를 사용하였으나 실제 코드 상으로는 $\mathbf{R} \in SO(3), \mathbf{t} \in \mathbb{R}^3$를 사용하였다. 따라서 회전 행렬 $\mathbf{R}$에 대한 covariance propagation된다[9].
\begin{equation} \begin{aligned}
\mathbf{C}_{t+1,i} + \mathbf{T}\mathbf{C}_{t,i}\mathbf{T}^{\intercal} \quad \rightarrow \mathbf{C}_{t+1,i} + \mathbf{R}\mathbf{C}_{t,i}\mathbf{R}^{\intercal}
\end{aligned}
\end{equation}
Gauss-Newton 수식 유도는 least-squares point-to-point ICP와 완전히 동일하다.
\begin{equation} \begin{aligned}
\mathbf{e}_i(\mathbf{x}+\Delta \mathbf{x}) \approx \mathbf{e}_i(\mathbf{x}) + \mathbf{J}_i\Delta \mathbf{x}
\end{aligned}
\end{equation}
$i$번째 점의 자코비안 또한 least-squares point-to-point ICP와 완전히 동일하다.
\begin{equation}
\boxed{
\begin{aligned}
\mathbf{J}_i & = \frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial [\mathbf{t}, \mathbf{R}]} \\
& = \frac{\partial \mathbf{e}_i(\mathbf{x}) }{\partial [\mathbf{t}, \Delta \mathbf{w}]} \quad \leftarrow {\color{Mahogany} \text{so(3)-based optimization} } \\
& =\frac{\partial }{\partial [\mathbf{t}, \Delta \mathbf{w}]} \bigg( \mathbf{R}\mathbf{p}_{t,i} + \mathbf{t} - \mathbf{p}_{t+1,i} \bigg) \\
& = \begin{bmatrix} 1 & 0 & 0 & 0 & z_{t,i}’ & - y_{t,i}’
\\ 0 & 1 & 0 & -z_{t,i}’ & 0 & x_{t,i}’ \\ 0 & 0 & 1 & y_{t,i}’ & -x_{t,i}’ & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 6}
\end{aligned} }
\end{equation}
- Lie theory-based optimization에 대한 내용은 에러와 자코비안 정리 포스팅을 참고하면 된다.
모든 점들에 대한 에러 함수를 합치면 다음과 같이 점군에 대한 에러 함수가 된다.
\begin{equation}
\begin{aligned}
& \mathbf{E}(\mathbf{x}) = \sum_i^n \| \mathbf{e}_i(\mathbf{x}) \|^2_{\mathbf{M}^{-1}} \\
& \mathbf{x} = \arg\min_{\mathbf{x}} \mathbf{E}(\mathbf{x})
\end{aligned}
\end{equation}
위 식을 자세하게 전개하면 (\ref{eq:gicp2}) 수식이 된다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{x} & = \arg\min_{\mathbf{x}} \mathbf{E}(\mathbf{x}) \\
& = \arg\min_{\mathbf{x}} \sum_i d_i^{\intercal} \mathbf{M} d_i
\end{aligned} }
\end{equation}
점군에 대한 자코비안 $\mathbf{J}_i$와 $\mathbf{H}_i, \mathbf{b}_i$도 다음과 같이 합쳐지게 된다. GICP는 확률 기반 모델링이기 때문에 공분산의 역행렬 $\mathbf{M}$이 곱해진 것에 유의한다.
\begin{equation}
\begin{aligned}
& \mathbf{H}_i = \mathbf{J}_i^{\intercal}\mathbf{M}\mathbf{J}_i \\
& \mathbf{b}_i = \mathbf{J}_i^{\intercal}\mathbf{M}\mathbf{e}_i
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \mathbf{J} = \sum_i^n \mathbf{J}_i \\
&\mathbf{H} = \sum_i^n \mathbf{H}_i\\
& \mathbf{b} = \sum_i^n \mathbf{b}_i
\end{aligned}
\end{equation}
GN 방법의 해는 다음과 같이 구할 수 있다. 유도 과정에 대해 궁금한 독자들은 에러와 자코비안 정리 포스팅을 참고하면 된다.
\begin{equation}
\begin{aligned}
\Delta \mathbf{x}^* = - \mathbf{H}^{-1}\mathbf{b}
\end{aligned}
\end{equation}
미소 증분량의 최적해 $\Delta \mathbf{x}^*$를 위와 같이 구했으면 이를 원래 상태 변수 $\mathbf{x}$에 업데이트 해준다. 업데이트를 통해 source 점군이 target 점군에 점진적으로 정합(registration)된다.
\begin{equation}
\begin{aligned}
\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*
\end{aligned}
\end{equation}
지금까지 설명한 과정을 source 점군이 더 이상 업데이트 되지 않을 때까지 반복한다. 이러한 과정을 Least squares GICP (3D ver.) 알고리즘이라고 부른다.
Gauss-Newton method (GICP 3D)
- Nearest neighborhood (e.g., KD-tree) 방법을 통해 source 점에 가장 가까운 target 점들을 correspondence로 설정한다.
- 공분산 $\mathbf{C}_{t,i}, \mathbf{C}_{t+1,i}$의 초기값을 설정한다. (fast_gicp[9]에서는 plane-to-plane 공분산이 기본값으로 설정되어 있음)
- (\ref{eq:gicp2})과 같이 에러함수를 정의한다. $\mathbf{e}(\mathbf{x})$
- 테일러 전개로 근사 선형화하여 자코비안을 구한다. $\mathbf{H} = \mathbf{J}^{\intercal}\mathbf{M}\mathbf{J}, \mathbf{b} = \mathbf{J}^{\intercal}\mathbf{M}\mathbf{e}$
- 1차 미분 후 0으로 설정한다. $\Delta \mathbf{x}^* = -\mathbf{H}^{-1}\mathbf{b}$
- 이 때 값을 구하고 이를 에러함수에 대입한다. $\mathbf{x} \leftarrow \mathbf{x} + \Delta \mathbf{x}^*$
- 값이 수렴할 때 까지 반복한다.
References
[2] (blog) ICP (Iterative Closest Point) 와 Point Cloud Registration - Jinsol Kim님 블로그
[3] (blog) Slam 3-2강 (ICP algorithm & Unknown Data Association) 요약 - taeyoung96님 블로그
[4] (youtube) [AIX7063] Inclass 19 | Iterative Closest Point 강의
[9] (code) SMRT-AIST/fast_gicp
p.s.) ICP의 과정에 대해 코드와 함께 상세하게 정리된 Jupyter notebook 링크를 공유한다. 애니메이션과 함께 매우 잘 정리되어있어 직관적으로 이해하기 쉬우니 참고하면 좋을 것 같다.
 A L I D A
A L I D A





