본 포스트는 공부 목적으로 작성하였습니다.
혹시 보시는 도중 잘못된 부분이나 개선할 부분이 있다면 댓글이나 메일주시면 확인 후 수정하도록 하겠습니다.
해당 포스트는 앞서 pdf 파일로 정리했던 자료를 포스팅한 글입니다.
자세한 내용은 다음 링크를 통해 확인해주세요.
https://www.facebook.com/groups/slamkr/permalink/809268749432771/
본 논문은 6자유도 ($x,y,z,\theta_x, \theta_y, \theta_z$) 공간에서 2-axis LiDAR 센서가 생성하는 데이터로 Odometry와 Mapping을 실시간으로 계산하는 SLAM 알고리즘을 제안하였다. 기존의 방법들은 주로 offline에서 loop closure를 활용해 drift를 최소화한 3D 맵을 만드는데 초점이 맞춰져있는 반면에, LOAM은 해당 문제를 자체적인 odometry 알고리즘과 mapping 알고리즘 2개로 나누어 병렬적으로 처리함으로써 low-drift, low-computational complexity의 특징을 지닌다.
LiDAR 센서는 다른 센서와 비교할 때 상대적으로 거리오차가 매우 작기 때문에 (대략 150m에 +-2.5cm 오차 발생 수준) 다양한 mapping 알고리즘이 연구되었다. LiDAR 센서가 정지한 채로 360 degree 회전을 하는 경우 mapping은 상대적으로 쉬우나 센서가 움직이면서 mapping을 하는 경우 lidar의 위치 및 방향을 계속 추정하면서 mapping을 해야한다. 이러한 문제를 해결하기 위해 기존에 제시된 방법들은 GPS/INS 센서 같은 LiDAR와 독립적인 센서로 LiDAR의 움직임을 추정하거나 wheel encoder를 사용해 로봇의 odometry를 추정하는 방법을 사용했다. 하지만 해당 방법들은 매 루프마다 로봇의 움직임을 누적시키면서 odometry를 추정하므로 드리프트 문제가 발생한다. 이러한 문제점을 해결하기 위해 저자는 LOAM 알고리즘을 개발하였고 드리프트를 최소화하는 것이 목적이므로 loop closure를 사용하지 않았다. 즉, front-ends만 사용하여 실험했다.
LiDAR Hardware

본 논문에서 사용한 센서는 위와 같다. Hokuyo UTM-30LX 센서를 사용하였으며 180도의 FOV를 가지고 0.25 degree의 해상력을 가지며 1초에 40라인씩 스캔이 가능하고 1초에 180 degree 회전이 가능한 센서 모듈이다.

Software System Overview

전반적인 LOAM의 시스템은 위와 같이 구성되어 있다. 이 때 변수의 의미는 다음과 같다.

$\hat{\mathcal{P}}$ : LiDAR로부터 들어오는 데이터 (Hokuyo이므로 2D laser scan data)
$\mathcal{P}_{k}$ : k번째 sweep을 통해 합쳐진 3D 포인트클라우드 데이터. odometry 계산과 mapping 계산에 모두 활용된다.
각 블록의 역할은 다음과 같다.
Lidar Odometry: 2개의 연속적인 Sweeps들을 받아서 relative motion을 계산하는 노드 (10 [hz])
Lidar Mapping: odometry를 바탕으로 계산된 undistorted 포인트클라우드의 offline map을 매칭하는 노드 (1 [hz])
Transform Integration: odometry와 mapping을 바탕으로 로봇의 현재 transform을 계산하는 노드
LiDAR Odometry
LiDAR Odometry는 크게 다음과 같이 3가지 알고리즘으로 구성되어 있다.
1. Feature Point Extraction
2. Finding Feature Point Correspondence
3. Motion Estimation
Feature Point Extraction

회전모터는 180 deg/s의 속도로 회전하고 Hokuyo 센서는 40 [hz] scan rate을 가지므로 2D laser scan과 수직방향의 해상도는 180/40 = 4.5 degree이다. 이 때, feature point는 sharp edge 또는 planar surface에 위치한 포인트로 정의한다.


$i$ : $\mathcal{P}_{k}$ 집합에 속한 임의의 한 점. $i \in \mathcal{P}_{k}$
$\mathcal{S}$ : 같은 laser scan 데이터에서 i점과 연쇄적으로(consecutive) 위치한 다른 점들의 집합
$\mathbf{X}^{L}_{(k,i)}$ : LiDAR 좌표계 $\{L\}$에서 $i \in \mathcal{P}_{k}$를 만족하는 i점의 좌표
위와 같이 정의했을 때 Local Surface의 smoothness $c$를 다음과 같이 나타낼 수 있다.
\begin{equation} \begin{aligned}
c = \left \| \frac{1}{\left | \mathcal{S} \right | \cdot \left \| \mathbf{X}^{L}_{(k,i)} \right \|} \right \| \left \| \sum_{j \in \mathcal{S}, j \neq i} (\mathbf{X}^{L}_{(k,i)} - \mathbf{X}^{L}_{(k,j)}) \right \|
\end{aligned} \end{equation}
해당 공식에 따라 c가 상대적으로 큰 포인트들은 edge feature, 상대적으로 작은 포인트들은 planar feature라고 정의한다. 위 계산을 모두 마치면 다음 과정을 수행한다.
1. 1개의 Laserscan 데이터를 4개의 동일한 subregion으로 분리한 후
2. c 값을 기준으로 points들을 재정렬한다.
3. 하나의 subregion에서는 최대 2 edge points와 4 planer points를 가지도록 설정한다.
4. 임의의 한 점 i 는 c 값이 특정 threshold를 넘는 경우에만 edge point 또는 planar point가 될 수 있도록 설정한다.
c 값을 바탕으로 feature point들을 선정할 때 다음과 같은 경우는 outlier로 분류하여 제외한다.
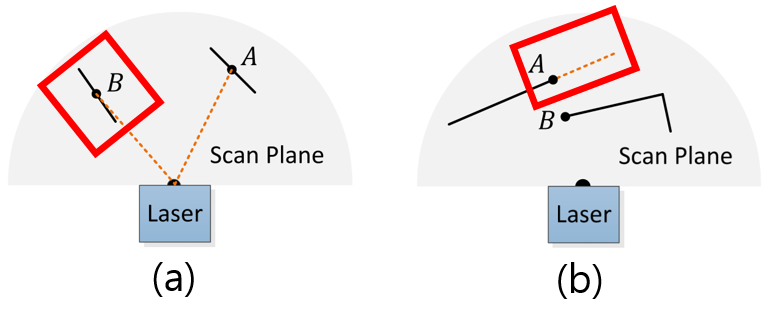
- laser beam과 거의 평행한 평면 내부의 점인 경우 $\rightarrow$ B점 근처 local surface의 법선 벡터를 구해서 laser beam과 각도를 계산한 후 수직에 가까울 경우 예외 처리한다.
- 음영지역으로 인해 edge가 아닌 점이 edge로 오인된 경우 $\rightarrow$ laser beam 방향으로 특정 갭 만큼 차이가 나는 경우 뒷 쪽에 해당하는 데이터는 예외처리한다.
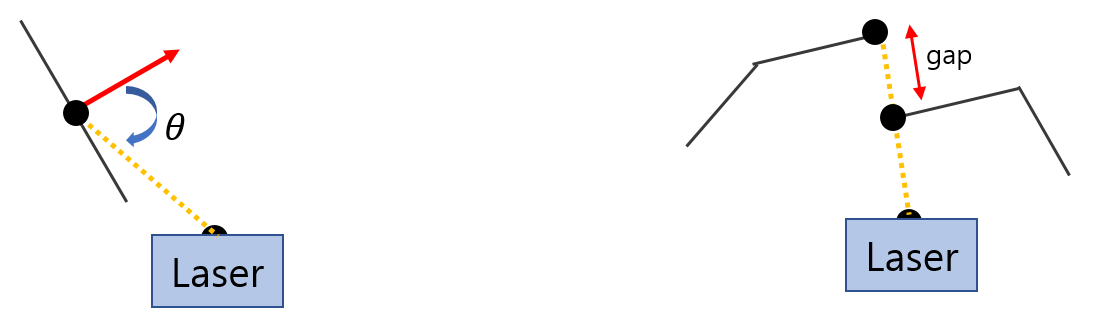
Finding Feature Point Correspondence
feature points 간의 상관관계를 계산하기 위해 sweeping 과정을 시간 순으로 표현하면 다음과 같다.
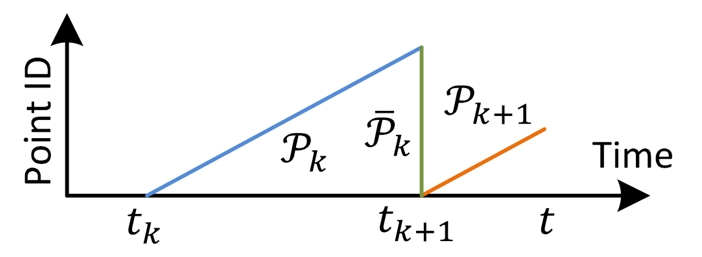
$t_k$ : k번째 sweep을 시작한 시점
$\mathcal{P}_{k}$ : k번째 sweep 동안 수집된 3D 포인트클라우드 데이터
$\bar{\mathcal{P}}_{k}$ : k+1번째 sweep이 시작되는 순간 reprojection된 k번째 포인트클라우드 데이터
$\mathcal{P}_{k+1}$ : k+1번째 sweep 동안 수집된 3D 포인트클라우드 데이터
여기서 $\bar{\mathcal{P}}_{k}$, $\mathcal{P}_{k+1}$ 모두 $t_{k+1}$ 시점에서 LiDAR의 모션을 추정하는데 사용된다. $\bar{\mathcal{P}}_{k}$와 $\mathcal{P}_{k+1}$ 데이터 간 상관관계를 찾는 작업이 feature points 간 상관관계를 찾는 작업을 의미한다.
$\mathcal{P}_{k+1}$은 $\begin{bmatrix}
\mathcal{E}_{k+1}\\
\mathcal{H}_{k+1}
\end{bmatrix}$와 같이 edge point, planar point의 집합으로 구성되어 있다. 따라서 결국 $\bar{\mathcal{P}}_{k}$와 $\begin{bmatrix}
\mathcal{E}_{k+1}\\
\mathcal{H}_{k+1}
\end{bmatrix}$ 사이의 상관관계를 구하는 문제가 된다. 하지만 $t_{k+1}$ 시점에서 $\mathcal{P}_{k+1}$는 아무 데이터도 없는 공집합이고 시간이 지남에 따라 sweep된 포인트들이 누적된다.
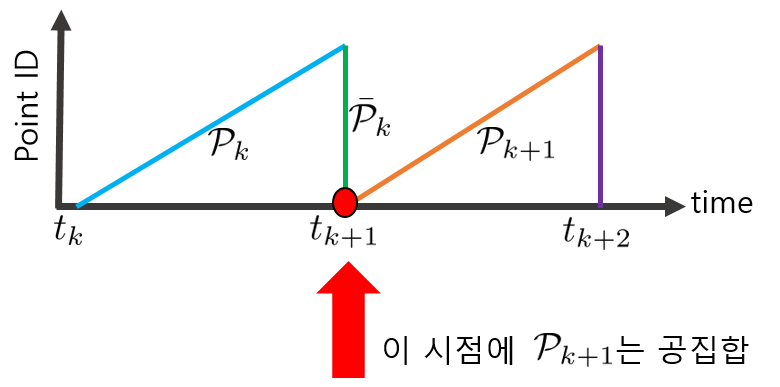
$\begin{bmatrix}
\mathcal{E}_{k+1}\\
\mathcal{H}_{k+1}
\end{bmatrix}$는 k+1번째 sweep이 다 끝난 시점인 $t_{k+2}$ 시점에 존재하는 데이터이다.
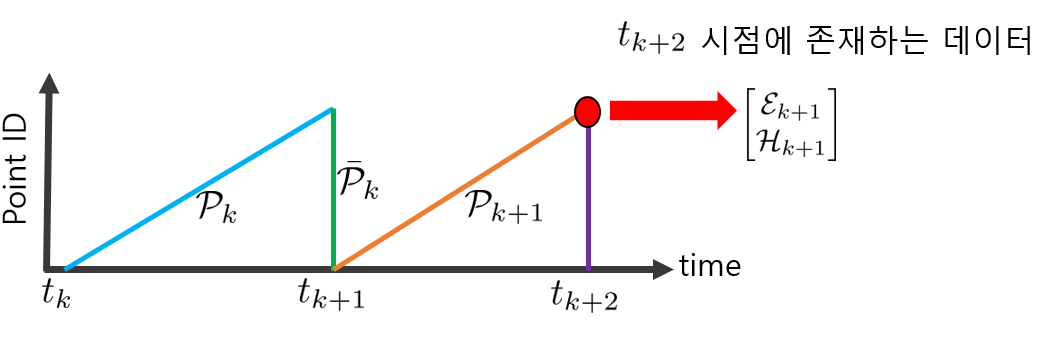
따라서 $\bar{\mathcal{P}}_{k}$와 상관관계를 구하려면 $t_{k+2} \rightarrow t_{k+1}$ 시점으로 reprojection이 필요하다.
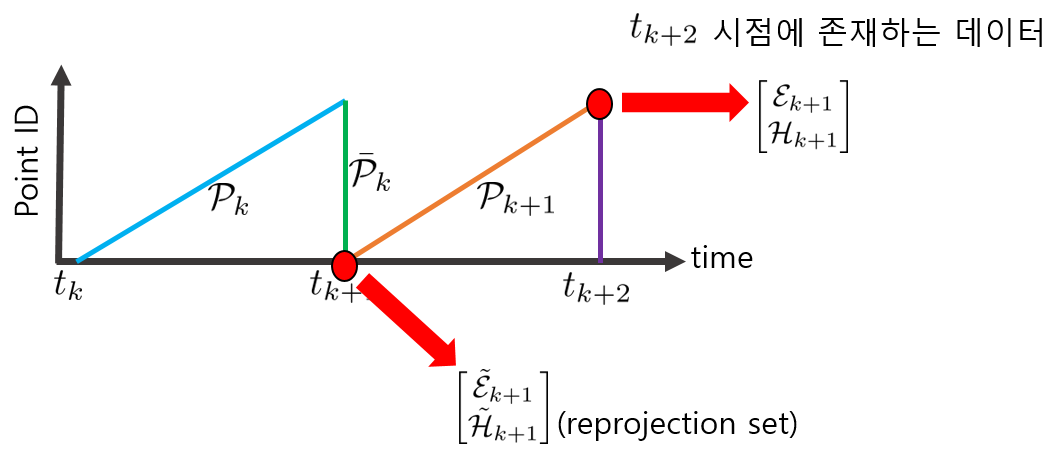
최종적으로 $\bar{\mathcal{P}}_{k}$와 $\begin{bmatrix}
\tilde{\mathcal{E}}_{k+1}\\
\tilde{\mathcal{H}}_{k+1}
\end{bmatrix}$는 closest neighbor point를 통해 상관관계를 구할 수 있다. 구체적인 과정은 다음과 같다.
edge point
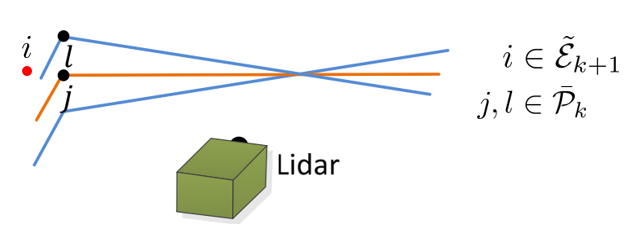
1. $i \in \tilde{\mathcal{E}}_{k+1}$를 만족하는 임의의 edge point $i$를 선택한다
2. $\bar{\mathcal{P}}_{k}$에서 cloest point인 $j$를 구한다. $(j \in \bar{\mathcal{P}}_{k})$
3. $j$와 연속적으로 위치한 다른 laserscan 상의 점 $l$ 또한 구한다. $(l \in \bar{\mathcal{P}}_{k})$
4. 이렇게 구한 $(j,l)$이 edge point라는 것을 증명하기 위해 local surface의 smoothness $c$를 계산한다.
5. $(j,l)$이 edge feature인 경우
\begin{equation} \begin{aligned}
d_{\mathcal{E}} = \frac{\left | (\tilde{\mathbf{X}}^{L}_{(k+1,i)} - \bar{\mathbf{X}}^{L}_{(k,j)}) \times (\tilde{\mathbf{X}}^{L}_{(k+1,i)} - \bar{\mathbf{X}}^{L}_{(k,l)}) \right |}{\left | \bar{\mathbf{X}}^{L}_{(k,j)} - \bar{\mathbf{X}}^{L}_{(k,l)} \right |}
\end{aligned} \end{equation}
공식을 사용해 $ \tilde{\mathcal{E}}_{k+1}$와 $\bar{\mathcal{P}}_{k}$ 간 거리를 구할 수 있다.
$\mathbf{X}^{L}_{(k,i)}$ : LiDAR 좌표계 $\{L\}$에서 $i \in \mathcal{P}_{k}$를 만족하는 $i$ 점의 좌표
planar point
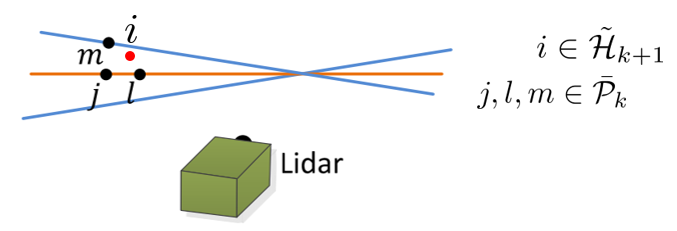
1. $i \in \tilde{\mathcal{H}}_{k+1}$를 만족하는 임의의 planar point $i$를 선택한다
2. $\bar{\mathcal{P}}_{k}$에서 closest point인 $j$를 구한다. $(j \in \bar{\mathcal{P}}_{k})$
3. $j$와 연속적으로 위치한 같은 laserscan 상의 점 $l$ 또한 구한다. $(l \in \bar{\mathcal{P}}_{k})$
4. $j$와 연속적으로 위치한 같은 laserscan 상의 점 $m$ 또한 구한다. $(m \in \bar{\mathcal{P}}_{k})$
5. 이렇게 구한 $(j,l,m)$이 planar points라는 것을 증명하기 위해 local surface의 smoothness c를 계산한다.
6. $(j,l,m)$이 planar feature인 경우
\begin{equation} \begin{aligned}
d_{\mathcal{H}} = \frac{\begin{vmatrix}
(\tilde{\mathbf{X}}^{L}_{(k+1,i)} - \bar{\mathbf{X}}^{L}_{(k,j)}) \\
((\bar{\mathbf{X}}^{L}_{(k,j)} - \bar{\mathbf{X}}^{L}_{(k,l)}) \times (\bar{\mathbf{X}}^{L}_{(k,j)} - \bar{\mathbf{X}}^{L}_{(k,m)}))\end{vmatrix}}
{\left | (\bar{\mathbf{X}}^{L}_{(k,j)} - \bar{\mathbf{X}}^{L}_{(k,l)}) \times (\bar{\mathbf{X}}^{L}_{(k,j)} - \bar{\mathbf{X}}^{L}_{(k,m)}) \right |}
\end{aligned} \end{equation}
를 사용해 $ \tilde{\mathcal{H}}_{k+1}$와 $\bar{\mathcal{P}}_{k}$ 간 거리를 구할 수 있다.
Motion Estimation
LiDAR 센서는 sweeping 하는 동안 등각속도 운동을 한다고 모델링한다.
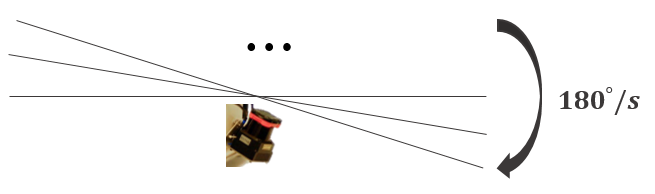
따라서 다른 시간대에 받은 센서 데이터를 통해 중간에 생략된 pose transform을 선형보간을 통해 계산할 수 있다. 예를 들어 $t_{k+1}$ 시점에 sweeping을 시작한다고 가정하면 $[t_{k+1}, t]$ 시간 사이의 LiDAR pose transform은 $\mathbf{T}_{k+1}^{L}$로 정의할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{T}_{k+1}^{L} = [t_{x},t_{y},t_{z},\theta_{x},\theta_{y},\theta_{z}]^{T}
\end{aligned} \end{equation}
- $L$ : LiDAR 좌표계
- $t_{x,y,z}$ : LiDAR 좌표계에서 병진운동
- $\theta_{x,y,z}$ : LiDAR 좌표계에서 회전운동(오른손법칙)
특정 한 점 $i$, $i \in \mathcal{P}_{k+1}$에 대한 $[t_{k+1}, t_{i}]$ 시간 사이의 pose transform은 $\mathbf{T}_{(k+1,i)}^{L}$로 나타낼 수 있고 이 때, 다음 선형보간 법칙이 성립한다.
\begin{equation} \begin{aligned}
\mathbf{T}_{(k+1,i)}^{L} = \frac{t_{i}-t_{k+1}}{t-t_{k+1}} \mathbf{T}_{k+1}^{L}
\end{aligned} \end{equation}
선형보간 법칙을 사용해서 $\begin{bmatrix}
\mathcal{E}_{k+1}\\
\mathcal{H}_{k+1}
\end{bmatrix}$ $\rightarrow$ $\begin{bmatrix}
\tilde{\mathcal{E}}_{k+1}\\
\tilde{\mathcal{H}}_{k+1}
\end{bmatrix}$ 변환을 수식으로 정리하면 다음과 같다.
\begin{equation} \begin{aligned}
\mathbf{X}^{L}_{(k+1,i)} = \mathbf{R} \tilde{\mathbf{X}}^{L}_{(k+1,i)} + \mathbf{T}^{L}_{(k+1,i)}(1:3)
\end{aligned} \end{equation}
- $\mathbf{X}^{L}_{(k+1,i)}$ : $\begin{bmatrix}
\mathcal{E}_{k+1}\\
\mathcal{H}_{k+1}
\end{bmatrix}$ 집합에 속한 임의의 한 점 $i$의 좌표
- $\tilde{\mathbf{X}}^{L}_{(k+1,i)}$ : $\begin{bmatrix}
\tilde{\mathcal{E}}_{k+1}\\
\tilde{\mathcal{H}}_{k+1}
\end{bmatrix}$ 집합에 속한 임의의 한 점 $i$의 좌표
- $\mathbf{T}_{(k+1,i)}^{L}(1:3) = [t_{x},t_{y},t_{z}]^{T}$ : $\mathbf{T}_{(k+1,i)}^{L}$에서 1~3번 항목만 사용
- $\mathbf{R} = e^{\hat{w}\theta} = \mathbf{I} + \hat{w}\sin \theta + \hat{w}^{2}(1-\cos \theta)$ : Rodrigues 공식을 통해 표현한 회전행렬
- $\theta= \left \| \mathbf{T}^{L}_{(k+1,i))}(4:6) \right \|$ : Rotation의 크기
- $\omega= \mathbf{T}^{L}_{(k+1,i))}(4:6)/\left \| \mathbf{T}^{L}_{(k+1,i))}(4:6) \right \|$ : Rotation 방향의 단위벡터
- $\hat{\omega}$ : $\omega$의 skew symmetric matrix
선형보간 공식들을 사용해서 앞서 사용한 $ \tilde{\mathcal{E}}_{k+1}$와 $\bar{\mathcal{P}}_{k}$의 거리를 구하는 공식을 함수화해서 표현하면 다음과 같다.
\begin{equation} \begin{aligned}
f_{\mathcal{E}}(\mathbf{X}^{L}_{(k+1,i)},\mathbf{T}^{L}_{k+1}) = d_{\mathcal{E}}, \ \ \ i \in \mathcal{E}_{k+1}
\end{aligned} \end{equation}
\begin{equation} \begin{aligned}
f_{\mathcal{H}}(\mathbf{X}^{L}_{(k+1,i)},\mathbf{T}^{L}_{k+1}) = d_{\mathcal{H}}, \ \ \ i \in \mathcal{H}_{k+1}
\end{aligned} \end{equation}
위 두 공식을 벡터화하여 표현하면 다음과 같다.
\begin{equation} \begin{aligned}
\mathbf{f}(\mathbf{T}^{L}_{k+1}) = \mathbf{d}
\end{aligned} \end{equation}
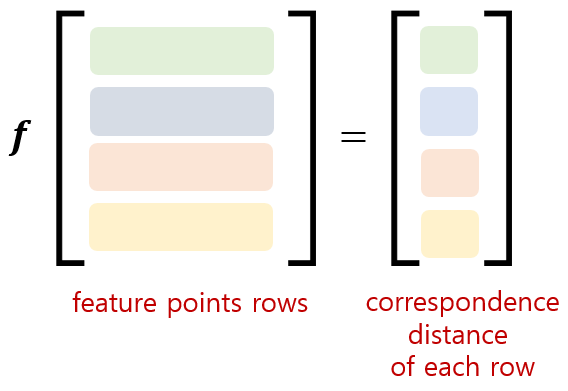
$d$ 값이 최소가 되는 $\mathbf{T}^{L}_{k+1}$를 비선형 최적화 방정식을 통해 구한다. 위 공식은 비선형이므로 $\mathbf{J} = \partial f/\partial \mathbf{T}^{L}_{k+1}$를 구한 다음 Levenberg-Marquardt(LM) 방식을 통해 최적화를 수행한다.
\begin{equation} \begin{aligned}
\mathbf{T}_{k+1}^{L} \leftarrow \mathbf{T}_{k+1}^{L} - (\mathbf{J}^{T}\mathbf{J} + \lambda \text{ diag}(\mathbf{J}^{T}\mathbf{J}))^{-1} \mathbf{J}^{T}\mathbf{d}
\end{aligned} \end{equation}
이 때, 에러 값은 bisquare weight 함수를 통해서 outlier에 강건하도록 설정한다.

지금까지의 LiDAR Odometry 과정을 요약하면 다음과 같다.

LiDAR Mapping
mapping 알고리즘은 10 [hz]로 수행되는 odometry 알고리즘과 달리 매 sweep이 끝나는 순간 (1 [hz] 주기)에 한 번만 수행된다. sweep이 끝날 때마다 odometry는 undistorted 포인트클라우드 $\bar{\mathcal{P}}_{k}$와 pose transform $\mathbf{T}^{L}_{k}$을 생성한다. 이 때, mapping 알고리즘은 $\bar{\mathcal{P}}_{k}$와 월드좌표계 $\{W\}$ 사이를 매칭하는 역할을 수행한다.
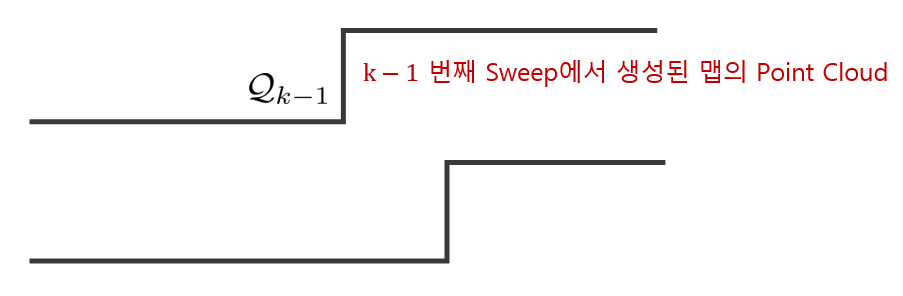
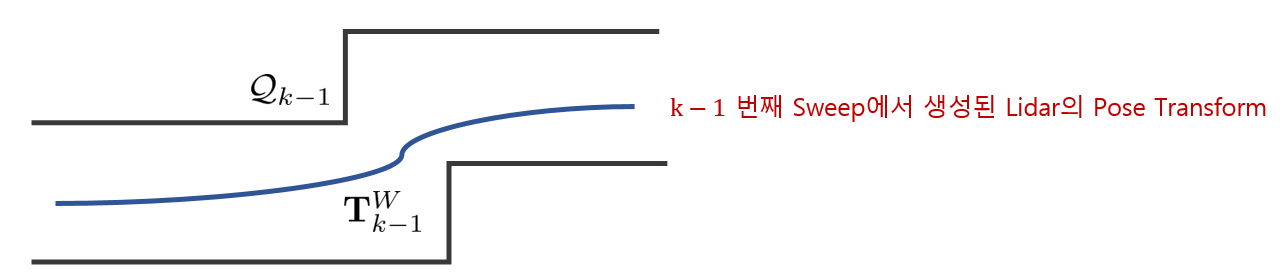
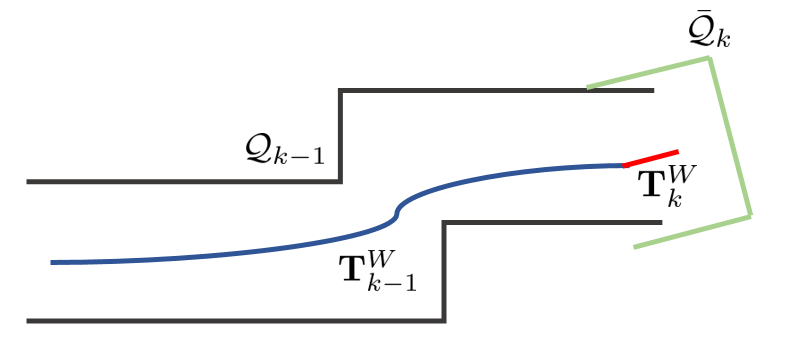
- $\mathcal{Q}_{k}$ : k번째 sweep에서 맵을 구성하는 포인트클라우드
- $\mathbf{T}^{W}_{k}$ : k번째 sweep에서 월드좌표계 $\{W\}$를 기준으로 본 LiDAR의 pose transform
- $\bar{\mathcal{Q}}_{k}$ : $\bar{\mathcal{P}}_{k}$에서 월드좌표계 $\{W\}$로 reprojection된 포인트클라우드
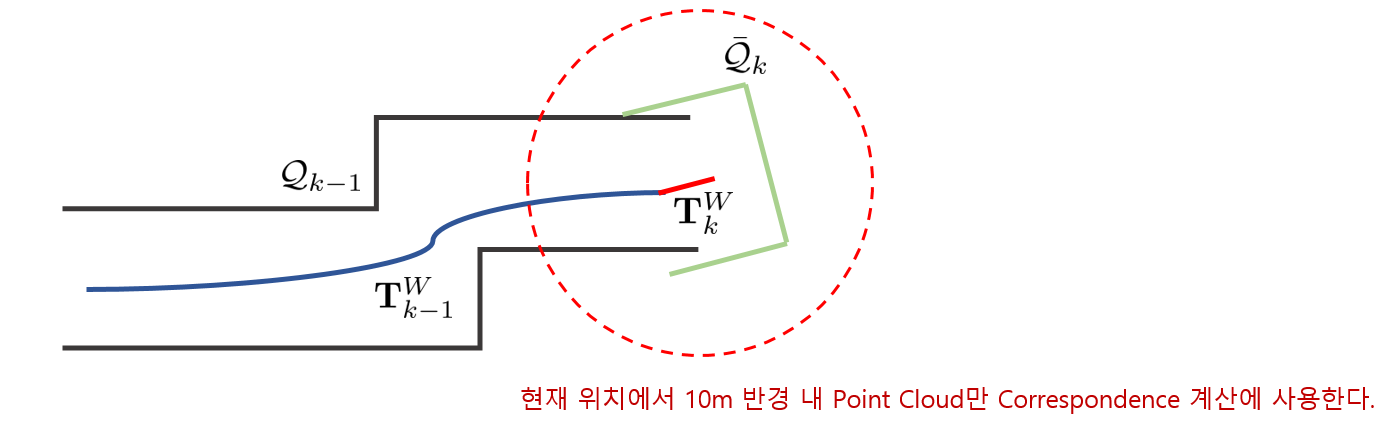
feature point를 추출하는 방법은 odometry와 동일하나 odometry보다 10배 많은 feature를 추출한다. (1 [hz]의 속도로 계산이 수행되므로). correspondence를 찾기 위해 현재 위치에서 반경 10 [m]의 포인트클라우드만 사용한다.
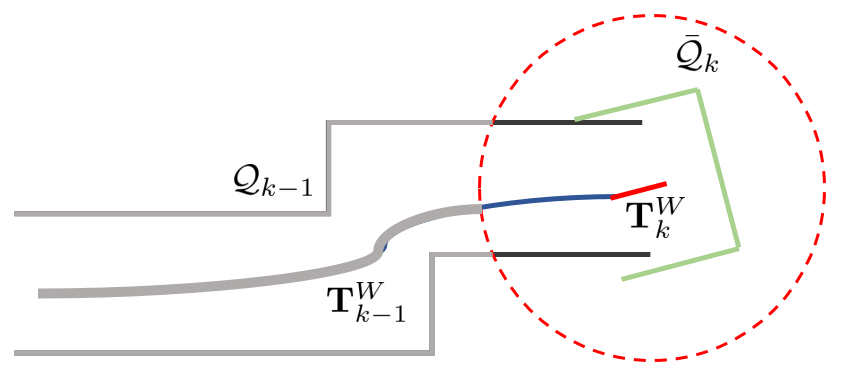
$\bar{\mathcal{Q}}_{k}$와 $\mathcal{Q}_{k-1}$ 사이의 correspondence를 찾은 다음 최적의 $\mathbf{T}^{W}_{k}$를 찾기 위해 최적화 과정을 수행해야 한다. correspondence를 찾는 방법은 다음과 같다. 우선 다음과 같이 정의한다.
- $\mathcal{S}^{'}$ : $\mathcal{Q}_{k-1}$에서 임의의 점들의 집합
- $\mathbf{M}$ : $\mathcal{S}^{'}$의 공분산 행렬
- $\mathbf{V}, \mathbf{E}$ : $\mathbf{M}$ 의 eigenvalue와 eigenvector
위와 같이 정의한 후 eigendecomposition을 수행한다. 이를 수행하는 edge feature는 $V_{1} >> V_{2},V_{3}$와 같은 특성을 가지고 planar feature는 $V_{1},V_{2} >> V_{3}$와 같은 특성을 지니므로 $V$ 값에 따라 해당 correspondence points가 어떤 feature인지 계산할 수 있다.
correspondence를 찾은 뒤에는 odometry 방식과 똑같은 공식을 사용하여 $d_{\mathcal{E}}, d_{\mathcal{H}}$를 구하고 LM 방법을 사용하여 최적화를 수행해서 최적의 $\mathbf{T}^{W}_{k}$를 계산한다.
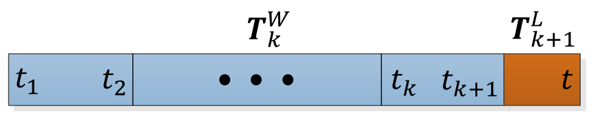
이렇게 계산된 $\mathbf{T}^{W}_{k}$는 sweep 당 한 번인 1 [hz]의 주기로 LiDAR 포즈를 업데이트하며 odometry는 $\mathbf{T}^{L}_{k+1}$를 10 [hz] 주기로 업데이트한다. 최종적으로 LiDAR 포즈는 위 두 값을 사용하여 odometry와 같은 10 [hz] 주기로 계산된다.
Reference
자료를 공부하면서 같이 참고하면 좋은 링크들을 아래 첨부하였다
1. LeGO-LOAM 관련 블로그 포스팅 by Hyungtae Lim님: https://limhyungtae.github.io/2022-03-27-LeGO-LOAM-Line-by-Line-1.-Introduction/
2. SLAMKR 스터디, LOAM 분석 영상 by Jinyong Jeong님 : https://youtu.be/snPzNmcbCCQ
'Engineering' 카테고리의 다른 글
| [SLAM] g2o example 코드 리뷰 (0) | 2022.06.09 |
|---|---|
| [SLAM] Visual LiDAR Odometry and Mapping (V-LOAM) 논문 리뷰 (0) | 2022.06.08 |
| [SLAM] Depth Enhanced Monocular Odometry (DEMO) 논문 리뷰 (0) | 2022.06.08 |
| [SLAM] Direct Sparse Odometry (DSO) 논문 및 코드 리뷰 (2) (11) | 2022.06.03 |
| [SLAM] Direct Sparse Odometry (DSO) 논문 및 코드 리뷰 (1) (5) | 2022.06.03 |
 A L I D A
A L I D A





