본 포스팅에서는 3차원 공간 상의 강체를 변환할 때 사용하는 다양한 표현법에 대해 설명한다.
Rigid body transformation
본 자료에서는 3차원 공간 상의 강체(rigid body)의 움직임을 수학적으로 표현하는 다양한 방법들에 대하여 설명한다. 강체란 이론적으로 무한대의 강성을 가지는 물체를 뜻한다. 따라서 강체는 외부에서 힘을 가해도 모양이 변형이 되지 않으며 무게중심으로 지정되는 하나의 점에 의해 운동이 결정된다.
SLAM에서 강체란 일반적으로 움직이는 카메라 센서를 의미하며 시간에 따라 카메라의 형태가 일정하다고 가정하므로 강체 변환(rigid body transformation)를 사용하여 카메라의 움직임을 수학적으로 표현할 수 있다.
Coordinate system
본 섹션에서는 이후 설명할 모든 변환의 기준이 되는 좌표계(coordinate system)에 대해 설명한다. 좌표계는 물체의 위치 및 방향을 수학적으로 표현할 수 있게 해주는 중요한 도구이다. 좌표계에 대해 자세히 이해하기 위해 아래 예시를 살펴 보자. 본 예시는 Keunjun님 블로그 포스팅의 내용을 주로 참고하였다.

예를 들어 두 사람이 하나의 돌을 바라보고 있을 때 돌을 표현하는 방법이 서로 다를 수 있다. A가 B에게 "돌이 어디에 어떤 자세로 있어?" 라고 물었을 때 B는 어떻게 대답해야 할까? 정답은 알 수 없다. 엄밀하게 말하면 질문에 오류가 있다.
- 어디를 기준으로 돌이 어디에 있는가?
- 돌의 표면 중 정확히 어느 점을 물어보고 있는가?
이처럼 물체의 위치와 자세를 이야기할 때 어디를 기준으로 표현하는가?(기준좌표계 $\{S\}$) 그리고 그 물체의 어디를 말하고자 하는가?(이동좌표계 $\{B\}$)를 명확하게 해야한다.

일반적으로 기준이 되는 좌표계 $\{S\}$를 기준좌표계(fixed frame, world frame, space frame)으로 부른다. 그리고 이동하는 물체를 대표하는 좌표계 $\{B\}$를 이동좌표계(moving frame, body frame)으로 부른다.
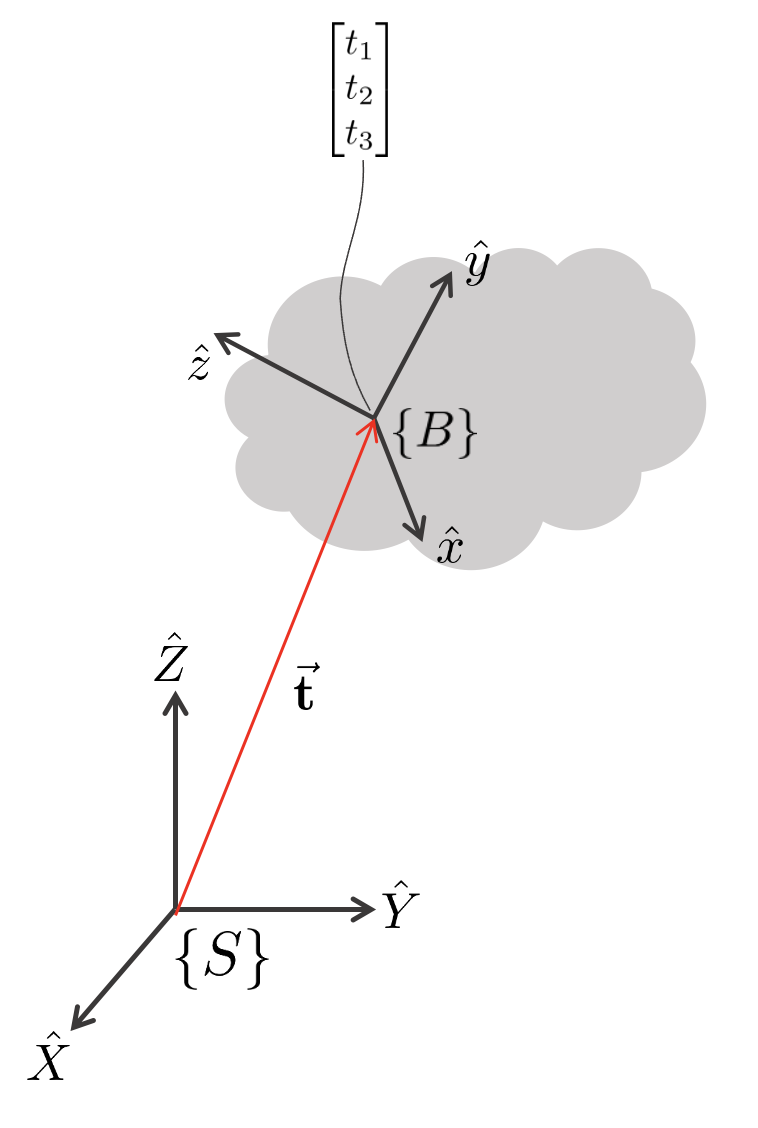
3D Example (Left Mouse : Drag, Right Mouse : Rotate, Wheel : Zoom) : 물체를 드래그 해보세요
강체의 경우 $\{B\}$ 좌표계를 아무 곳이나 물체의 한 곳에 잡으면 된다. 보통은 무게중심에 잡는다. $\{B\}$ 좌표계가 움직여도 강체는 형태가 변하지 않으므로 강체의 다른 부분의 위치가 자동으로 결정된다. 이동좌표계 $\{B\}$ 의 원점을 $\vec{\mathbf{t}}$, 축을 $(\hat{x},\hat{y},\hat{z})$라고 하고 기준좌표계 $\{S\}$ 의 축을 $(\hat{X},\hat{Y},\hat{Z})$라고 하자. 이 때 기준좌표계 $\{S\}$ 를 기준으로 이동좌표계 $\{B\}$의 원점을 표현해보면 다음과 같다.
\begin{equation}
\begin{aligned}
\vec{\mathbf{t}}=t_1\hat{X}+t_2\hat{Y}+t_3\hat{Z} \quad \cdots \text{ \{B\}'s origin}
\end{aligned} \label{eq:coord1}
\end{equation}
다음으로 이동좌표계 $\{B\}$ 의 축 $(\hat{x},\hat{y},\hat{z})$ 를 $(\hat{X},\hat{Y},\hat{Z})$ 의 선형결합으로 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
&\hat{x}=r_{11}\hat{X}+r_{21}\hat{Y}+r_{31}\hat{Z}
\\ & \hat{y}=r_{12}\hat{X}+r_{22}\hat{Y}+r_{32}\hat{Z} \quad \cdots \text{ \{B\}'s axis}
\\ & \hat{z}=r_{13}\hat{X}+r_{23}\hat{Y}+r_{33}\hat{Z}
\end{aligned} \label{eq:coord2}
\end{equation}
Rotation matrix
앞서 설명한 $\{B\}$ 좌표계의 표현 (\ref{eq:coord1}), (\ref{eq:coord2})를 합쳐서 표시하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \vec{\mathbf{t}}=t_1\hat{X}+t_2\hat{Y}+t_3\hat{Z}
\\ &\hat{x}=r_{11}\hat{X}+r_{21}\hat{Y}+r_{31}\hat{Z}
\\ &\hat{y}=r_{12}\hat{X}+r_{22}\hat{Y}+r_{32}\hat{Z}
\\ & \hat{z}=r_{13}\hat{X}+r_{23}\hat{Y}+r_{33}\hat{Z}
\end{aligned}
\end{equation}
위 식을 벡터와 행렬 형태로 나타내면 다음과 같이 간결하게 나타낼 수 있다.
\begin{equation}
\begin{aligned}
& \vec{\mathbf{t}}= \mathbf{t}^{\intercal} \begin{bmatrix} \hat{X} \\ \hat{Y} \\ \hat{Z} \end{bmatrix} \quad \quad \quad \begin{bmatrix} \hat{x} \\ \hat{y} \\ \hat{z} \end{bmatrix} = \mathbf{R} \begin{bmatrix} \hat{X} \\ \hat{Y} \\ \hat{Z} \end{bmatrix}
\end{aligned} \label{eq:rot1}
\end{equation}
이 때, $(\hat{X},\hat{Y},\hat{Z}) \rightarrow (\hat{x},\hat{y},\hat{z})$ 변환은 크기는 변하지 않고 오직 회전에만 관여하는데 이러한 변환에 사용하는 행렬 $\mathbf{R}$ 을 회전 행렬(rotation matrix) 이라고 한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{R} = \begin{bmatrix} r_{11}&r_{12}&r_{13} \\ r_{21}&r_{22}&r_{23} \\ r_{31}&r_{32}&r_{33} \end{bmatrix} \in \mathbb{R}^{3\times 3}
\end{aligned} }
\end{equation}
$\mathbf{R}$ 은 보통 $^{S}_{B}\mathbf{R}$ 또는 $\mathbf{R}_{SB}$ 로 표기한다. 이 표현의 의미는 다음과 같이 두 가지로 해석할 수 있다.
- 행렬 자체로 봤을 때: $\{S\}$ 좌표계에서 바라본 $\{B\}$ 좌표계의 회전(량) 또는 방향 (orientation of $\{B\}$ frame with respect to $\{S\}$ frame)
- 연산자로 봤을 때: 점 또는 벡터를 $\{B\} \rightarrow \{S\}$ 좌표계로 변환하는 연산자
이는 다음 섹션에서 자세하게 설명한다.
Properties of rotation matrix
이젠 섹션에서 본 것과 같이 $\{B\}$ 좌표계를 표현하려면 다음과 같이 12개의 파라미터가 필요하다.
\begin{equation}
\begin{aligned}
(t_{1} , t_{2} , t_{3}), (r_{11}, r_{12}, r_{13}, r_{21}, r_{22}, r_{23}, r_{31}, r_{32}, r_{33})
\end{aligned}
\end{equation}
하지만 3차원 공간에서 물체는 회전 3자유도(roll, pitch, yaw)와 이동 3자유도(x,y,z)를 합한 6자유도(=6dof, 6 degree of freedom)를 갖는다. 이에 따라 12개의 변수는 모두 독립이 아니고 종속적이라는 것을 알 수 있다. 즉, 회전 행렬에서 3개의 값을 독립적으로 정하면 제약조건에 의해 나머지 6개의 변수는 결정된다는 것을 알 수 있다. 회전 행렬의 제약 조건은 다음과 같다.
- $\{B\}$ 좌표계의 축들은 단위벡터라는 조건
\begin{equation}
\begin{aligned}
\begin{array}{ll} \text{(i) } & \left | \hat{x} \right |^2 = 1: r_{11}^2+r_{21}^2+r_{31}^2=1 \\ \text{(ii) } & \left | \hat{y} \right |^2 = 1: r_{12}^2+r_{22}^2+r_{32}^2=1 \\ \text{(iii) } & \left | \hat{z} \right |^2 = 1: r_{13}^2+r_{23}^2+r_{33}^2=1 \end{array}
\end{aligned}
\end{equation} - $\{B\}$ 좌표계의 축들은 서로 수직하다는 조건
\begin{equation}
\begin{aligned}
\begin{array}{ll} \text{(iv) } & \hat{x} \perp \hat{y} : r_{11}r_{12}+r_{21}r_{22}+r_{31}r_{32}=0 \\ \text{(v) } & \hat{x} \perp \hat{z} : r_{11}r_{13}+r_{21}r_{23}+r_{31}r_{33}=0 \\ \text{(vi) } & \hat{y} \perp \hat{z} : r_{12}r_{13}+r_{22}r_{23}+r_{32}r_{33}=0 \end{array}
\end{aligned}
\end{equation}
- 위 조건들을 합쳐서 보통 다음과 같이 표현한다. $(\text{i}\sim\text{vi}) \quad \mathbf{R}^\text{T}\mathbf{R}=\mathbf{I}$.
- 이를 회전 행렬의 직교 성질(orthogonal property)라고 한다.
- (일반적으로) 오른손 좌표계를 사용한다는 조건
\begin{equation}
\begin{aligned}
\text{(vii) det}\mathbf{R}=1 \Leftrightarrow \hat{x} \times \hat{y} = \hat{z}
\end{aligned}
\end{equation} - 다음과 같은 연속적인 회전을 나타낼 때는 회전 행렬의 곱셈을 통해 표현할 수 있다.

\begin{equation}
\begin{aligned}
^{a}_{b}\mathbf{R}^{b}_{c}\mathbf{R} \ =\ ^{a}_{c}\mathbf{R}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\color{red}{[\hat{x}_{b},\hat{y}_{b},\hat{z}_{b}] = [\hat{x}_{a},\hat{y}_{a},\hat{z}_{a}]^{a}_{b}R}
\\ \color{red}{[\hat{x}_{c},\hat{y}_{c},\hat{z}_{c}] = [\hat{x}_{b},\hat{y}_{b},\hat{z}_{b}]^{b}_{c}R}
\\ \color{blue}{\therefore [\hat{x}_{c},\hat{y}_{c},\hat{z}_{c}] = [\hat{x}_{a},\hat{y}_{a},\hat{z}_{a}]^{a}_{c}R^{b}_{c}R}
\end{aligned}
\end{equation}
- $\{a\} \rightarrow \{b\}$ 만큼 회전한 다음 다시 $\{b\} \rightarrow \{a\}$ 만큼 회전하면 원래 $\{a\}$ 좌표계가 된다. 즉, 회전하지 않은 것과 동일하다.

\begin{equation}
\begin{aligned}
^{a}_{b}\mathbf{R}^{b}_{a}\mathbf{R} = \mathbf{I}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
^{a}_{b}\mathbf{R}\ ^{a}_{b}\mathbf{R}^\text{T}=\mathbf{I} \quad \text{and} \quad ^{a}_{b}\mathbf{R}\ ^{b}_{a}\mathbf{R} = \mathbf{I}
\end{aligned}
\end{equation}
- 위 식으로부터 회전 행렬은 역행렬과 전치행렬이 동일 하며 이는 반대방향으로 회전을 나타냄을 알 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{R}^\text{T}\mathbf{R}=\mathbf{I} \quad \leftrightarrow \quad \mathbf{R}^{\text{T}} = \mathbf{R}^{-1} \\
& \therefore \ ^{a}_{b}\mathbf{R}^{-1} = \ ^{a}_{b}\mathbf{R}^{T} = \ ^{b}_{a}\mathbf{R}
\end{aligned}
\end{equation} - 회전 행렬을 통해 특정 벡터의 기준 좌표계 또한 변환할 수 있다.

- $\vec{\mathbf{v}}$ 벡터를 $\{a\}$ 좌표계와 $\{b\}$ 좌표계에서 각각 표현하면 다음과 같다.

- 이 때 $\{b\}$ 좌표계는 $\{a\}$ 좌표계와 회전 행렬을 통해 표현이 가능하므로

- 따라서 아래와 같이 특정 벡터의 기준좌표계를 회전 행렬을 통해 변환할 수 있다.

- $\vec{\mathbf{v}}$ 벡터를 $\{a\}$ 좌표계와 $\{b\}$ 좌표계에서 각각 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \vec{\mathbf{v}}_a \ = \ ^{a}_{b}\mathbf{R}\vec{\mathbf{v}}_b
\end{aligned}
\end{equation}
- 회전 행렬을 사용하여 특정 벡터를 회전시킬 수도 있다.
\begin{equation}
\begin{aligned}
\mathbf{v}' \ = \ ^{a}_{b}\mathbf{Rv}
\end{aligned}
\end{equation}
- 좌표계가 회전할 때 좌표계 위에 있는 사람이 보면 벡터가 회전하는 것처럼 보인다.
- 좌표계가 회전할 때 좌표계 위에 있는 사람이 보면 벡터가 회전하는 것처럼 보인다.

SO(3) group
회전 행렬과 같이 순수한 회전에만 관여하는 행렬을 따로 군(group)으로 묶을 수 있다. Lie 군 중 하나인 Special Orthogonal 3(SO(3))군은 3차원 회전 행렬(rotation matrix)과 이에 닫혀있는 연산들로 구성된 군을 의미하며 3차원 물체의 회전을 표현할 때 사용 한다.
\begin{equation}
\begin{aligned}
SO(3) = \{ \mathbf{R} \in \mathbb{R}^{3 \times 3} \ | \ \mathbf{R}\mathbf{R}^{T} = \mathbf{I}, \text{det}(\mathbf{R})=1 \}
\end{aligned}
\end{equation}
SO(3)군에 대한 자세한 내용은 Lie Theory 개념 정리 (SO(3), SE(3)) 포스트를 참조하면 된다.
Transformation matrix
이전 섹션에서는 회전 행렬 $\mathbf{R}$을 통한 강체의 순수한 회전에 대해 다뤘다. 하지만 3차원 공간 상의 물체는 회전 $\mathbf{R}$과 이동 $\mathbf{t}$을 모두 표현할 수 있어야하므로 회전 행렬만으로는 부족하다. 따라서 해당 섹션에서는 물체의 회전과 이동을 한 번에 표현할 수 있는 변환 행렬 (transformation matrix) $\mathbf{T}$에 대해 설명한다.
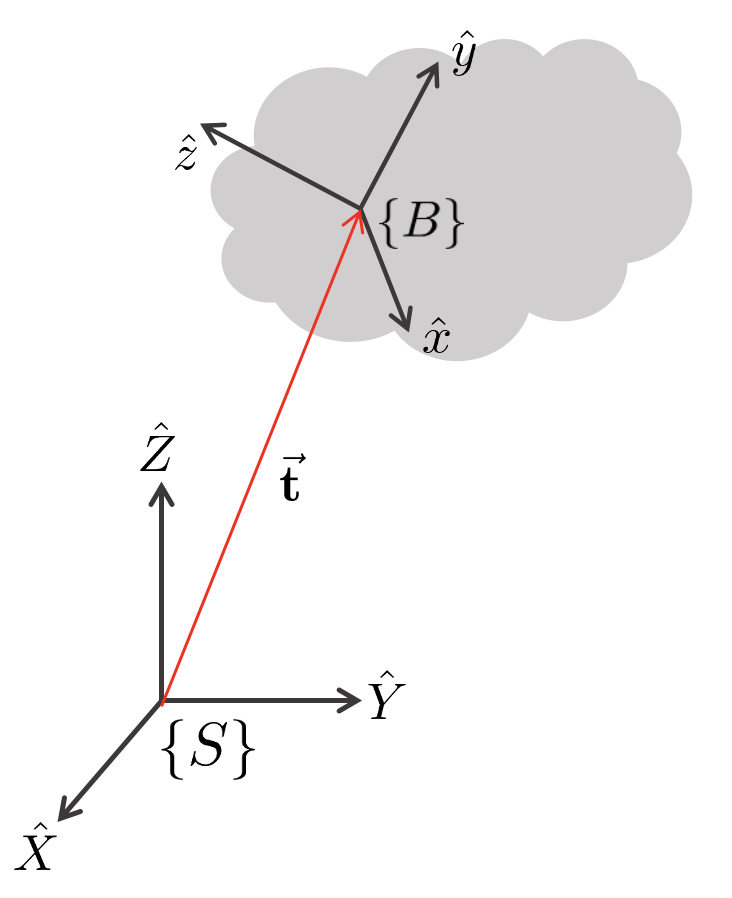
다시 위 그림으로 돌아와서 고정좌표계 $\{S\}$를 기준으로 바위에 붙어있는 이동좌표계 $\{B\}$를 표현해보자. 지금까지 정의한 식으로 나타내면 (\ref{eq:rot1})과 같다.
\begin{equation}
\begin{aligned}
& \vec{\mathbf{t}}= \mathbf{t}^{\intercal} \begin{bmatrix} \hat{X} \\ \hat{Y} \\ \hat{Z} \end{bmatrix} \quad \quad \quad \begin{bmatrix} \hat{x} \\ \hat{y} \\ \hat{z} \end{bmatrix} = \mathbf{R} \begin{bmatrix} \hat{X} \\ \hat{Y} \\ \hat{Z} \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathbf{t} = [t_1, t_2, t_3]^{\intercal}$
- $\mathbf{R} = \begin{bmatrix} r_{11}&r_{12}&r_{13} \\ r_{21}&r_{22}&r_{23} \\ r_{31}&r_{32}&r_{33} \end{bmatrix}$
위 식은 원점에 대한 표현 $\vec{\mathbf{t}}$와 좌표계 회전에 대한 표현 $[\hat{x}, \hat{y}, \hat{z}]^{\intercal}$을 분리해서 나타내고 있다. 변환 행렬 $\mathbf{T}$를 사용하면 다음과 같이 이동과 회전을 한 번에 표현할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{T} = \left[\begin{array}{ccc|c} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ \hline 0 & 0 & 0 & 1 \end{array}\right] = \left[\begin{array}{cc} \mathbf{R} & \mathbf{t} \\ 0 & 1 \end{array}\right] \in \mathbb{R}^{4\times 4}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \begin{bmatrix}
\hat{x}\\ \hat{y}\\ \hat{z}\\1
\end{bmatrix}=
\mathbf{T} \begin{bmatrix}
\hat{X}\\ \hat{Y}\\ \hat{Z}\\1
\end{bmatrix}
\end{aligned}
\end{equation}
이 때, 변환 행렬 $\mathbf{T}$ 의 마지막 행은 항상 $\begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}$ 인데 이는 3차원 벡터와 점을 동차 좌표계(homogeneous coordinate)로 표현했기 때문이다. 따라서 변환 행렬은 동차 변환 행렬(homogeneous transformation matrix)라고도 불린다. 동차 좌표계에 대한 자세한 내용은 Multiple View Geometry in Computer Vision 책 내용 정리 포스팅을 참고하면 된다.
Properties of transformation matrix
회전 행렬과 동일하게 변환 행렬 $\mathbf{T}$ 또한 $\{B\}$ 좌표계를 표현하려면 다음과 같이 12개의 파라미터가 필요하다.
\begin{equation}
\begin{aligned}
(t_{1} , t_{2} , t_{3}), (r_{11}, r_{12}, r_{13}, r_{21}, r_{22}, r_{23}, r_{31}, r_{32}, r_{33})
\end{aligned}
\end{equation}
하지만 3차원 공간에서 물체는 회전 3자유도와 이동 3자유도를 합한 6자유도(=6dof, 6 degree of Freedom)를 갖는다. 그리고 회전은 3자유도를 가지므로 이에 따라 12개의 변수는 모두 독립이 아니고 종속적이라는 것을 알 수 있다. 변환 행렬은 회전 행렬을 포함하므로 회전 행렬의 제약 조건을 모두 가진다. 변환 행렬의 성질은 다음과 같다.
- 연속적인 변환을 나타낼 때는 변환 행렬의 곱셈을 통해 표현할 수 있다.

\begin{equation}
\begin{aligned}
& ^{a}_{b}\mathbf{T}^{b}_{c}\mathbf{T} \ =\ ^{a}_{c}\mathbf{T} \quad \text{where, } ^{a}_{c}\mathbf{T} = \ (^{a}_{c}\mathbf{R},\ ^{a}_{c}\mathbf{t})=\left[\begin{array}{cc} ^{a}_{c}\mathbf{R} & ^{a}_{c}\mathbf{t} \\ 0 & 1 \end{array}\right]
\end{aligned}
\end{equation}
- $\{a\} \rightarrow \{b\}$로 변환한 다음 다시 $\{b\} \rightarrow \{a\}$로 변환하면 원래 $\{a\}$ 좌표계가 된다. 즉, 변환하지 않은 것과 동일하다.
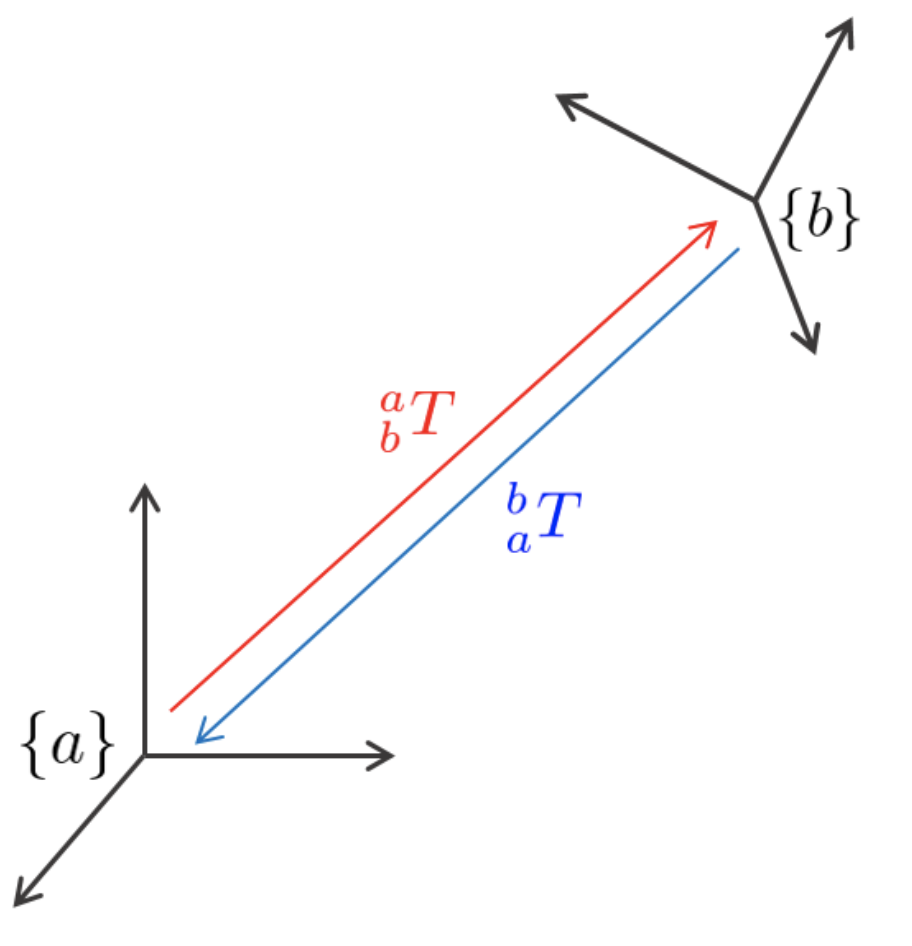
\begin{equation}
\begin{aligned}
^{a}_{b}\mathbf{T}^{b}_{a}\mathbf{T} = \mathbf{I}
\end{aligned}
\end{equation}
- 변환 행렬의 역행렬은 다음과 같다. 회전 행렬은 $\mathbf{R}^{-1}=\mathbf{R}^{T}$ 이지만 변환 행렬은 $\mathbf{T}^{-1} \neq \mathbf{T}^{T}$ 이다.
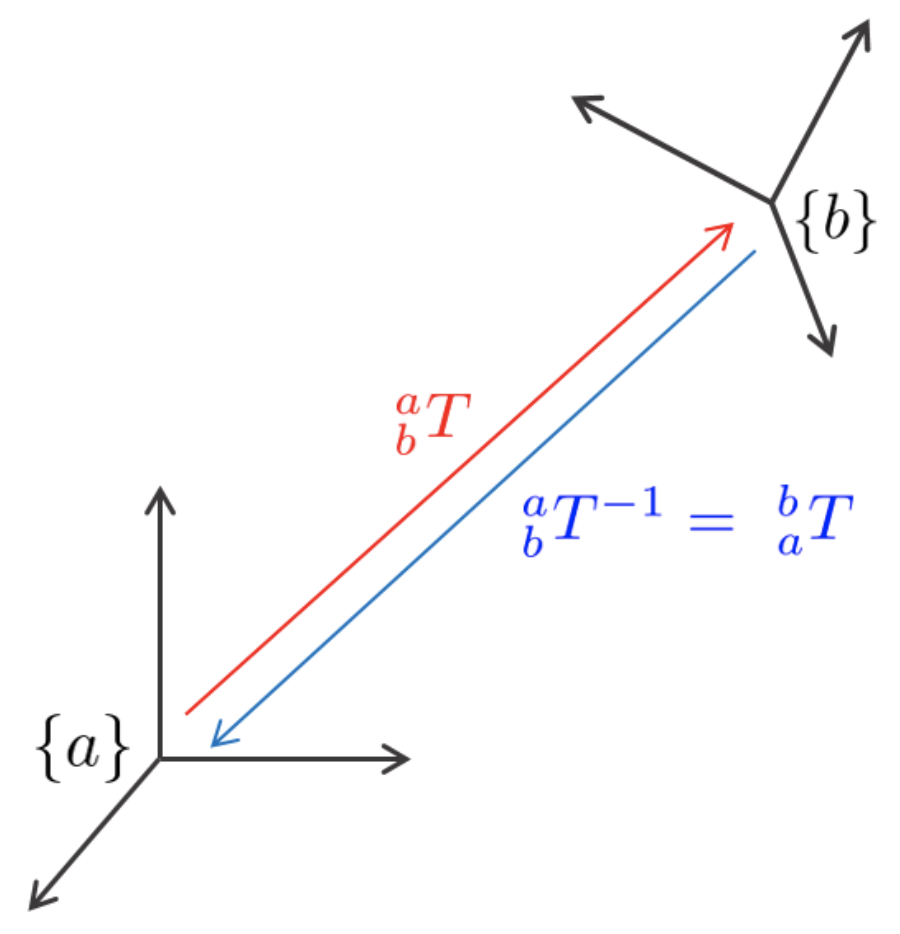
\begin{equation}
\begin{aligned}
& ^{a}_{b}\mathbf{T} = \left[\begin{array}{cc} ^{a}_{b}\mathbf{R} & ^{a}_{b}\mathbf{t} \\ 0 & 1 \end{array}\right] \\
& ^{a}_{b}\mathbf{T}^{-1} = \ ^{b}_{a}\mathbf{T} = \left[\begin{array}{cc} ^{a}_{b}\mathbf{R}^{T} & {\color{red}{-^{a}_{b}\mathbf{R}^{T}\ ^{a}_{b}\mathbf{t}}} \\ 0 & 1 \end{array}\right]
\end{aligned}
\end{equation}
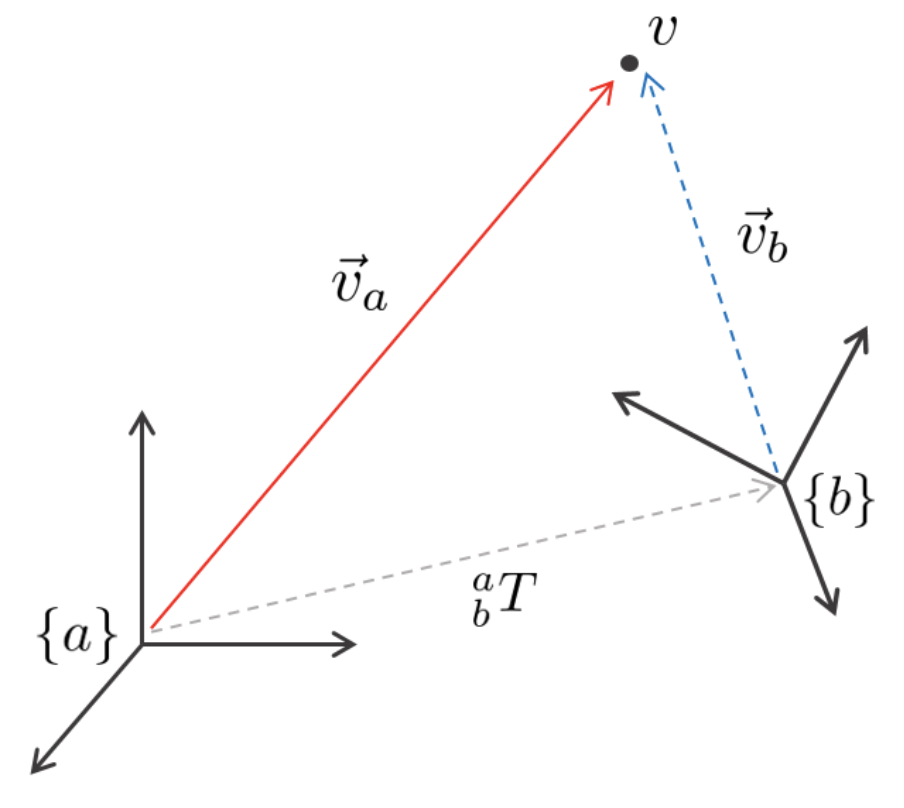
- $\{b\}$ 좌표계에서 3차원 공간 상의 점 $\mathbf{v}$ 를 표현하면 $\vec{\mathbf{v}}_{b}$ 와 같고 이를 $\{a\}$ 좌표계에서 $\vec{\mathbf{v}}_{a}$ 로 표현하기 위해서는 아래와 같은 변환이 필요하다.
\begin{equation}
\begin{aligned}
& \vec{\mathbf{v}}_{a} = \ ^{a}_{b}\mathbf{R}\vec{\mathbf{v}}_{b} + \ ^{a}_{b}\mathbf{t} \\
& \vec{\mathbf{v}}_{a} = \ ^{a}_{b}\mathbf{T}\vec{\mathbf{v}}_{b}
\end{aligned}
\end{equation}
- 좌표계 뿐만 아니라 특정 벡터를 회전 및 이동하는 연산자로써 변환 행렬을 사용할 수 있다. 두 $\{a\}$ 좌표계 위의 벡터 $\vec{\mathbf{v}}_{1}, \vec{\mathbf{v}}_{2}$ 의 변환관계는 다음과 같이 표현할 수 있다.
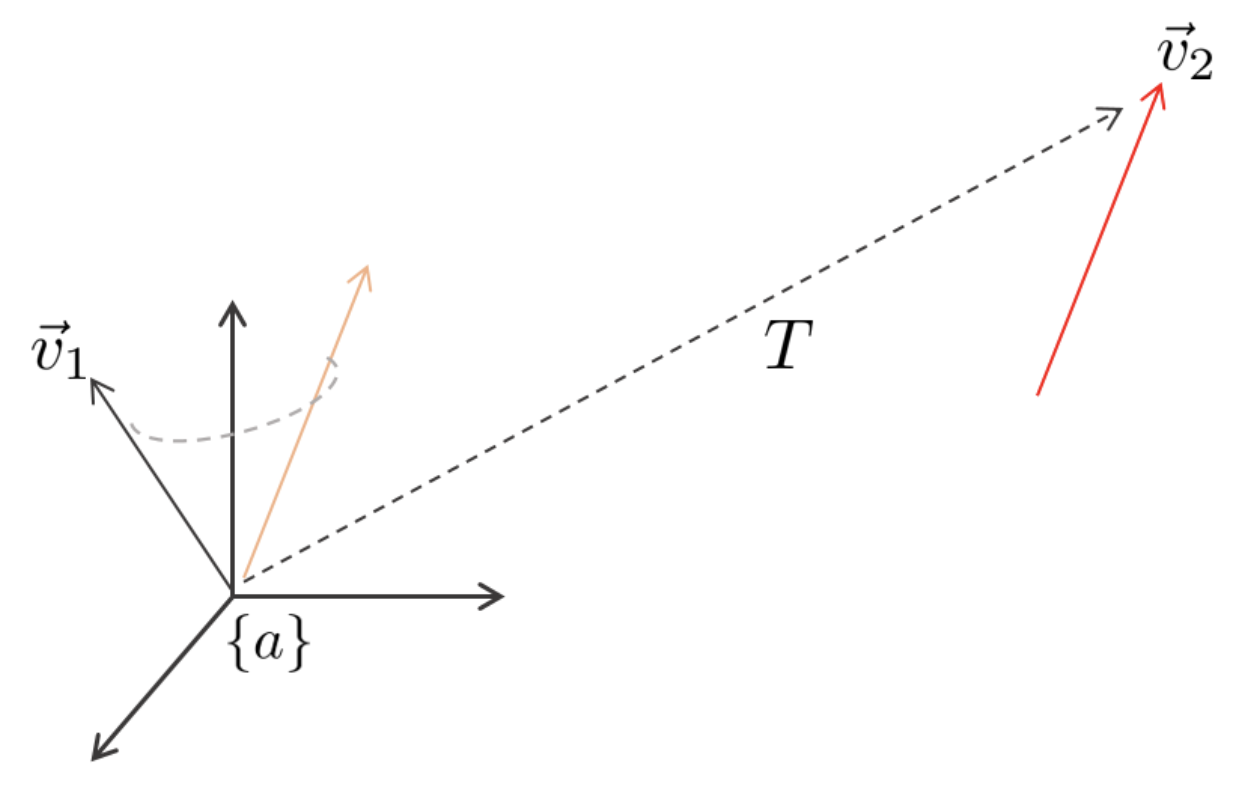
\begin{equation}
\begin{aligned}
& \begin{bmatrix} x_{v_{2}}\\ y_{v_{2}}\\ z_{v_{2}}\\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{13} & r_{13} & p_{x}\\ r_{21} & r_{22} & r_{23} & p_{y} \\ r_{31} & r_{32} & r_{33} & p_{z}\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{v_{1}}\\ y_{v_{1}}\\ z_{v_{1}}\\ 1 \end{bmatrix} \\
& \vec{\mathbf{v}}_{2} = \mathbf{T}\vec{\mathbf{v}}_{1}
\end{aligned}
\end{equation}
SE(3) group
변환 행렬과 같이 물체의 회전과 이동에 관여하는 행렬을 따로 군(group)으로 묶을 수 있다. Lie 군 중 하나인 Special Euclidean 3(SE(3))군은 3차원 변환 행렬(transformation matrix)과 이에 닫혀있는 연산들로 구성된 군을 의미하며 3차원 물체의 변환을 표현할 때 사용 한다.
\begin{equation}
\begin{aligned}
SE(3) = \left \{ \mathbf{T} =
\begin{bmatrix}
\mathbf{R} & \mathbf{t} \\
\mathbf{0} & 1
\end{bmatrix} \in \mathbb{R}^{4\times4} \ | \ \mathbf{R} \in SO(3), \mathbf{t} \in \mathbb{R}^{3} \right \}
\end{aligned}
\end{equation}
SE(3)군에 대한 자세한 내용은 Lie Theory 개념 정리 (SO(3), SE(3)) 포스트를 참조하면 된다.
Other rotation representations
Euler angle
오일러 각도(euler angle) 표현법은 3차원 물체의 방향(orientation)을 3개의 서로 직교하는 $X,Y,Z$축 각도로 표현하는 방법 중 하나이다. 3개의 각도로 물체의 방향을 표현할 때 크게 고정 각도(fixed angle)표현법과 오일러 각도(euler angle) 표현법이 있는데 오일러 각도는 회전한 축을 기준으로 다음 회전을 한다는 점 이 고정 각도 표현법과 다르다. 아래 그림과 같이 $z,y$축을 순차적으로 돌리는 경우를 생각해보자. 오일러 각도는 회전한 축을 기준으로 다음 회전이 적용된다.
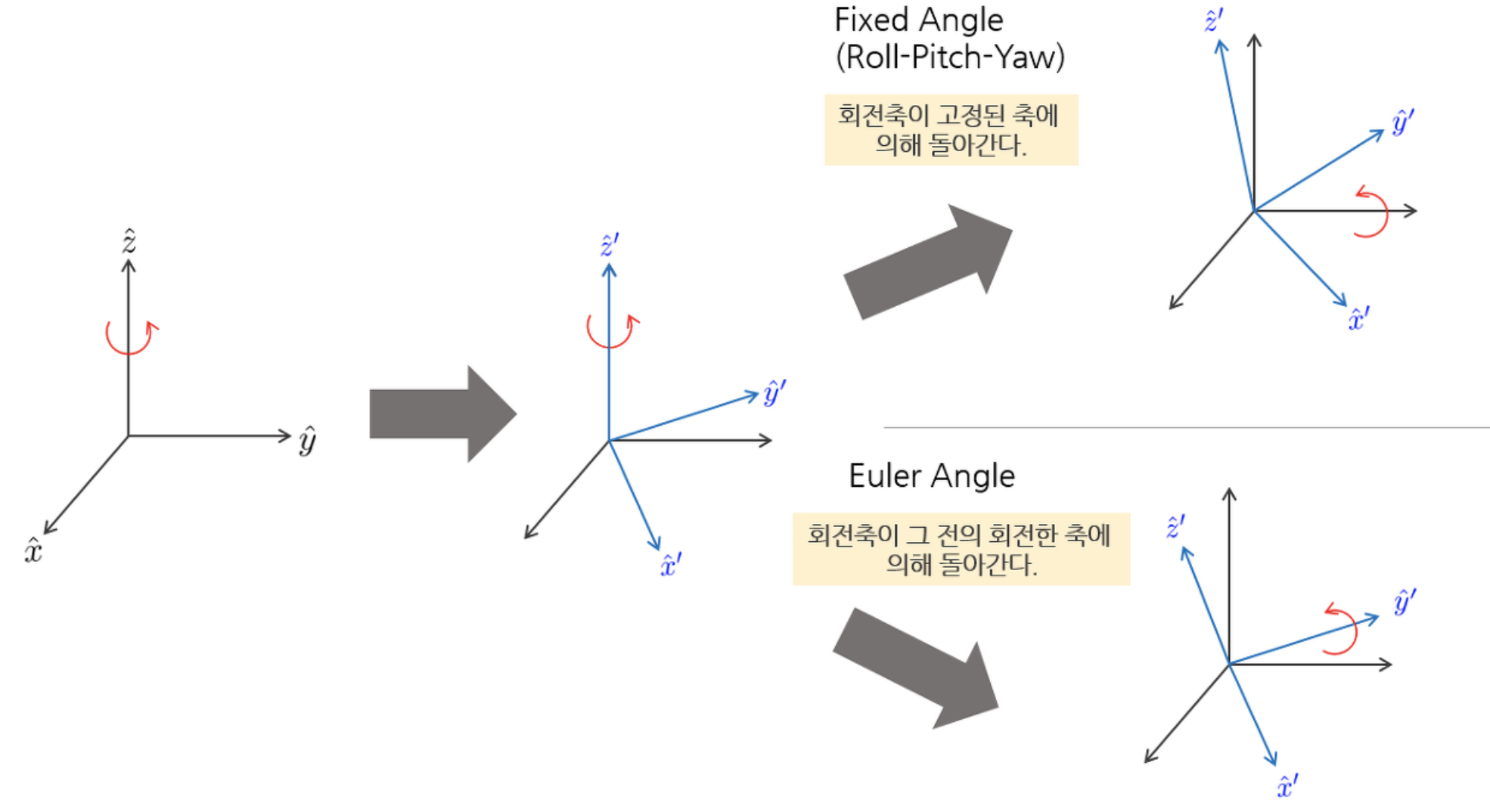
예를 들어, 오일러 각도가 $x,y,z$ 축 순서로 $(\gamma, \beta, \alpha)$ 라고 하면 이는 우선 $x$ 축으로 $\gamma$ 만큼 회전한 다음, 회전한 축 $(x^{'},y^{'},z^{'})$ 의 $y^{'}$ 축을 기준으로 $\beta$ 만큼 회전한다. 그리고 마지막으로 회전한 축 $(x^{''},y^{''},z^{''})$ 의 $z^{''}$ 축을 기준으로 $\alpha$ 만큼 회전한다.
Various euler angle representations
오일러 각도는 회전 순서에 따라 XYZ,ZXY,ZXZ,XYX,YXY,YZY,ZYZ,ZXZ,XZY,YXZ,YZX,ZYX와 같이 12개의 서로 다른 표현법이 존재한다. 각 회전은 이전 회전에 종속적이며 교환법칙이 성립하지 않으므로 축을 돌리는 순서를 아는 것이 중요하다. 예를 들어 ZYX의 경우 아래 그림과 같다.
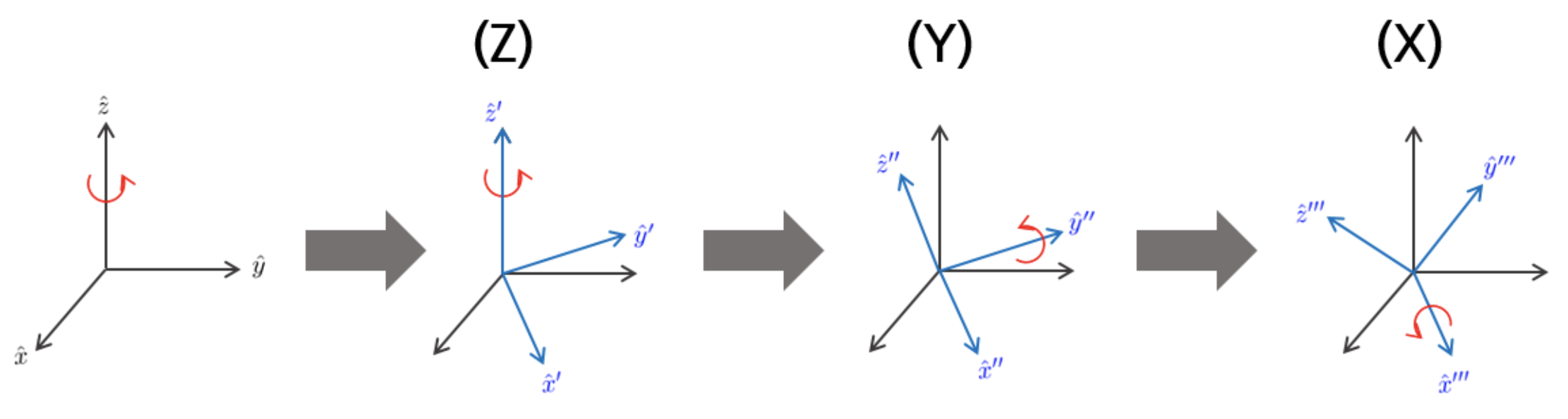
이 때, 오일러 각도는 다음과 모든 회전을 같이 하나로 합쳐서 표현한다.
\begin{equation}
\begin{aligned}
R_{ZYX} \left(\alpha,\beta,\gamma\right) & =\text{Rot}\left(\hat{z},\alpha\right) \text{Rot}\left(\hat{y},\beta\right)\text{Rot}\left(\hat{x},\gamma\right) = R_{Z}\left(\alpha\right)R_{Y}\left(\beta\right)R_{X}\left(\gamma\right) \\
& = \begin{bmatrix}
c_{\alpha}c_{\beta} & c_{\alpha}s_{\beta}s_{\gamma}-s_{\alpha}c_{\gamma} & c_{\alpha}s_{\beta}c_{\gamma}+s_{\alpha}s_{\gamma} \\ s_{\alpha}c_{\beta} & s_{\alpha}s_{\beta}s_{\gamma}+c_{\alpha}c_{\gamma} & s_{\alpha}s_{\beta}c_{\gamma}-c_{\alpha}s_{\gamma}\\ -s_{\beta} & c_{\beta}s_{\gamma} & c_{\beta}c_{\gamma} \end{bmatrix}
\end{aligned} \label{eq:euler1}
\end{equation}
Relationship between euler angle and rotation matrix
모든 오일러 각도는 회전 행렬로 변환이 가능하다. 아래 그림과 같이 $\hat{x}, \hat{y}, \hat{z}$ 축을 기준으로 좌표계를 각각 $\gamma, \beta, \alpha$ 만큼 회전시킬 때 회전 행렬은 다음과 같다.
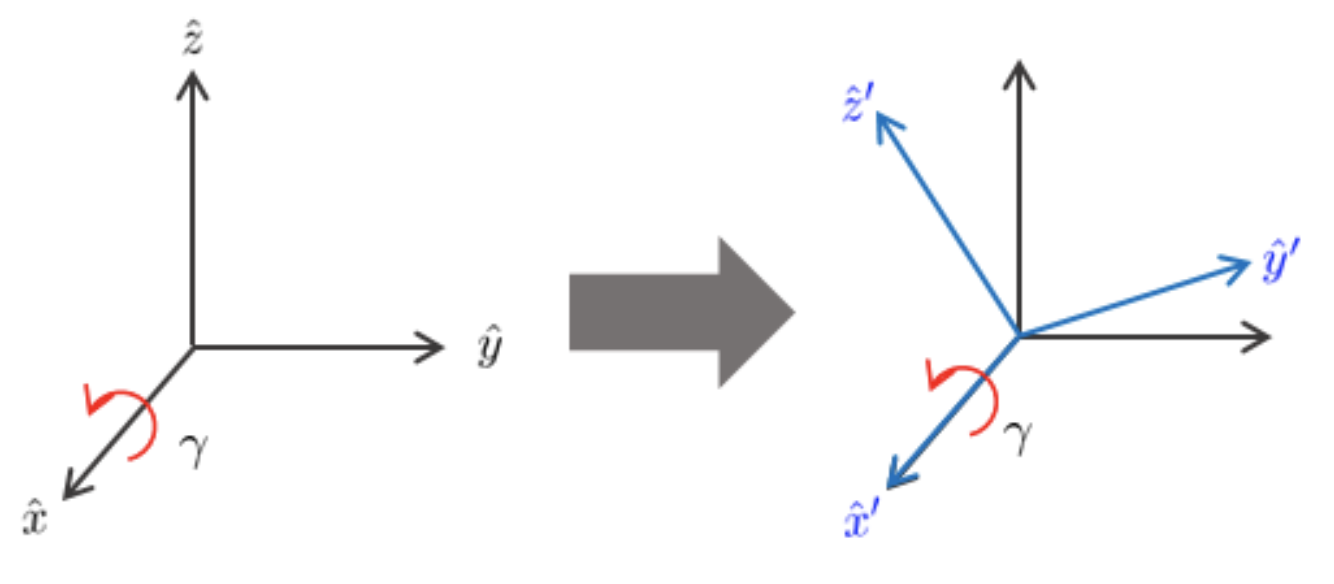
\begin{equation}
\begin{aligned}
R_{x}\left(\gamma\right) = \text{Rot}\left(\hat{x},\gamma \right) = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos{\gamma } & -\sin{\gamma } \\ 0 & \sin{\gamma } & \cos{\gamma } \end{array}\right]
\end{aligned}
\end{equation}
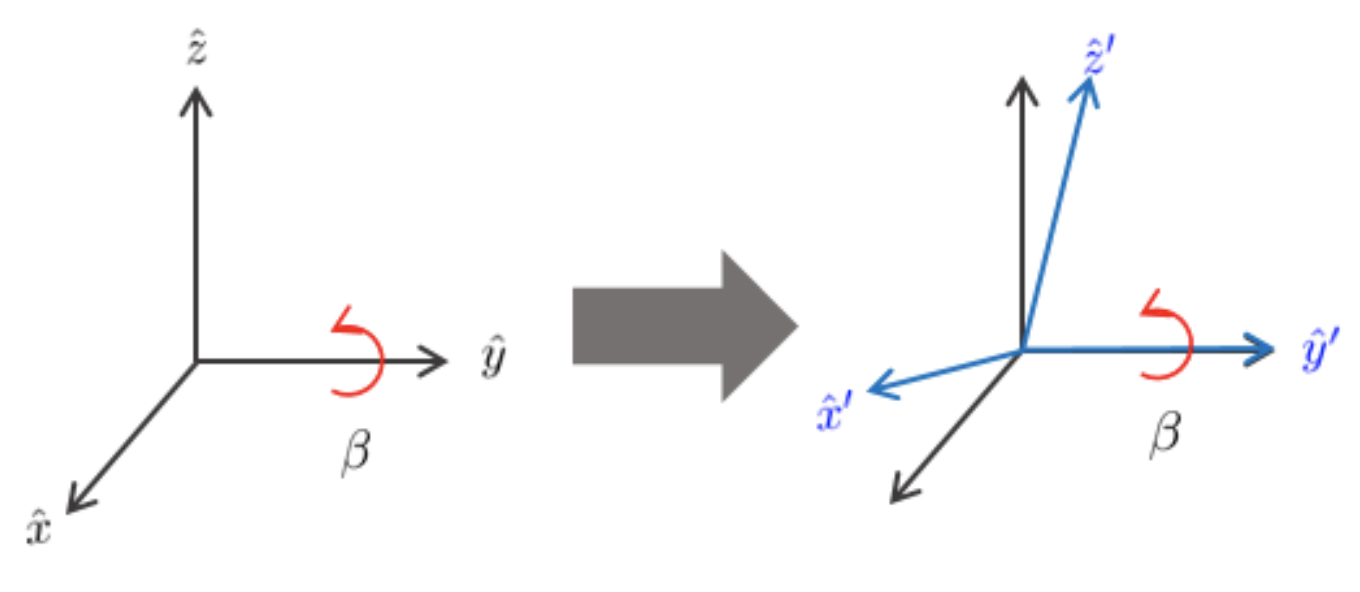
\begin{equation}
\begin{aligned}
R_{y}\left(\beta\right) = \text{Rot}\left(\hat{y},\beta\right) = \left[\begin{array}{ccc} \cos{\beta} & 0 & \sin{\beta} \\ 0 &1 & 0 \\ -\sin{\beta} & 0 & \cos{\beta} \end{array}\right]
\end{aligned}
\end{equation}
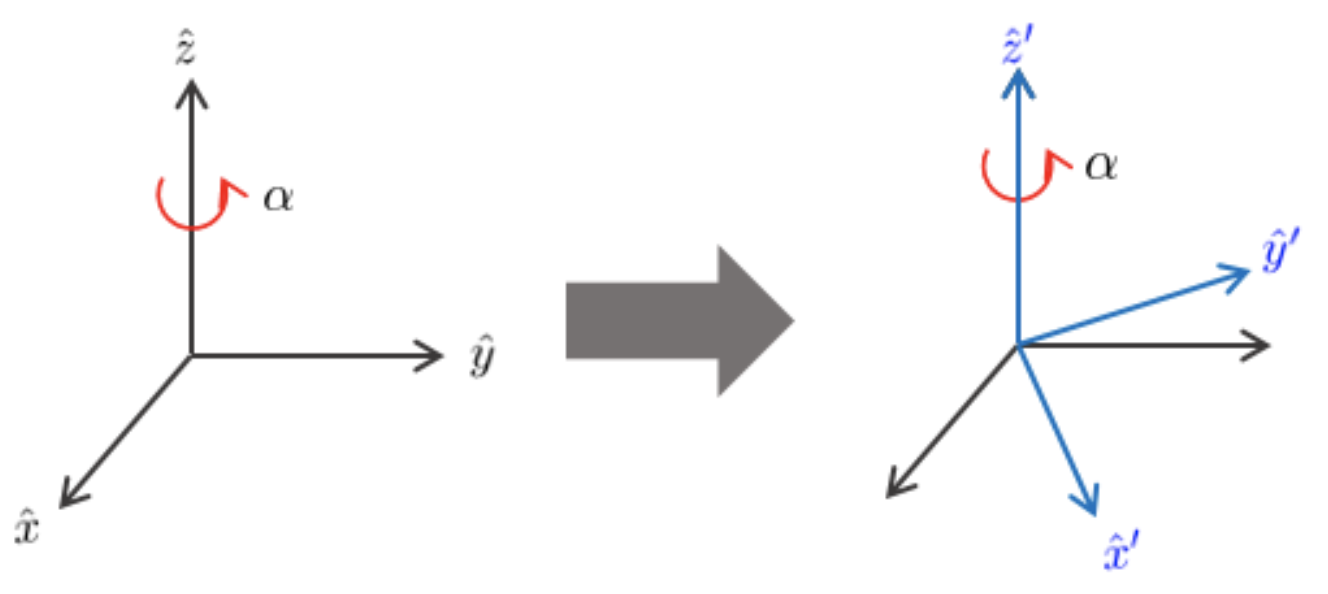
\begin{equation}
\begin{aligned}
R_{z}\left(\alpha\right) = \text{Rot}\left(\hat{z},\alpha\right) = \left[\begin{array}{ccc} \cos{\alpha} & -\sin{\alpha} & 0 \\ \sin{\alpha} & \cos{\alpha} & 0 \\ 0 & 0 & 1 \end{array}\right]
\end{aligned}
\end{equation}
Limitation of euler angle
오일러 각도는 3차원 상의 물체의 방향(orientation)을 3개의 파라미터만으로 간결하게 표현할 수 있다는 점과 대략적인 방향에 대한 직관적인 정보를 준다는 점에서 좋지만 다음과 같은 한계점들을 가지고 있다.
- Gimbal Lock: 오일러 각도 표현 법은 짐벌락이라는 치명적인 문제점을 가지고 있다. 오일러 각도로 물체를 표현할 때 같은 방향으로 두 회전 축이 겹치는 경우 해당 2개의 축이 더이상 분리되지 않는 고정 상태 가 되는데 이를 짐벌락이라고 한다. 따라서 3개의 자유도 중 1개의 자유도를 잃어버리게 되므로 다양한 방향 표현이 불가능해진다. 짐벌락 유튜브
- Interpolation: 오릴러 각도 표현법은 고정 각도 표현법과 다르게 3축에 대해 회전이 종속적이므로 2개의 오일러 각도 사이를 보간(interpolation)할 때에도 문제가 발생한다. 이는 컴퓨터로 구현할 때 문제가 된다. 따라서 물체의 방향(orientation)을 표현할 때는 오일러 각도를 종종 사용하지만 물체의 회전(rotation)을 표현할 때는 오일러 각도를 거의 사용하지 않는다.
- 예를 들어 $R_{ZYX}(0,180,0) = R_{ZYX}(180,0,180)$ 은 같은 물체의 방향(orientation)을 표현한다. 이 때 $(0,0,0) \rightarrow (0,180,0)$ 으로 보간하는 경우 중간값은 $(0,90,0)$ 이지만 $(0,0,0) \rightarrow (180,0,180)$ 으로 보간하는 경우 중간값은 $(90,0,90)$ 이 되어 서로 완전 다른 방향으로 회전하게 된다.
- 예를 들어 $R_{ZYX}(0,180,0) = R_{ZYX}(180,0,180)$ 은 같은 물체의 방향(orientation)을 표현한다. 이 때 $(0,0,0) \rightarrow (0,180,0)$ 으로 보간하는 경우 중간값은 $(0,90,0)$ 이지만 $(0,0,0) \rightarrow (180,0,180)$ 으로 보간하는 경우 중간값은 $(90,0,90)$ 이 되어 서로 완전 다른 방향으로 회전하게 된다.
Fixed angle (roll-pitch-yaw)
고정 각도(fixed angle) 표현법은 3차원 물체의 방향(orientation)을 3개의 서로 직교하는 $x,y,z$축 각도로 표현하는 방법 중 하나이다. 3개의 각도로 물체의 방향을 표현할 때 크게 고정 각도(fixed angle)표현법과 오일러 각도(euler angle) 표현법이 있는데 고정 각도는 고정된 축을 기준으로 다음 회전을 한다는 점 이 오일러 각도 표현법과 다르다.
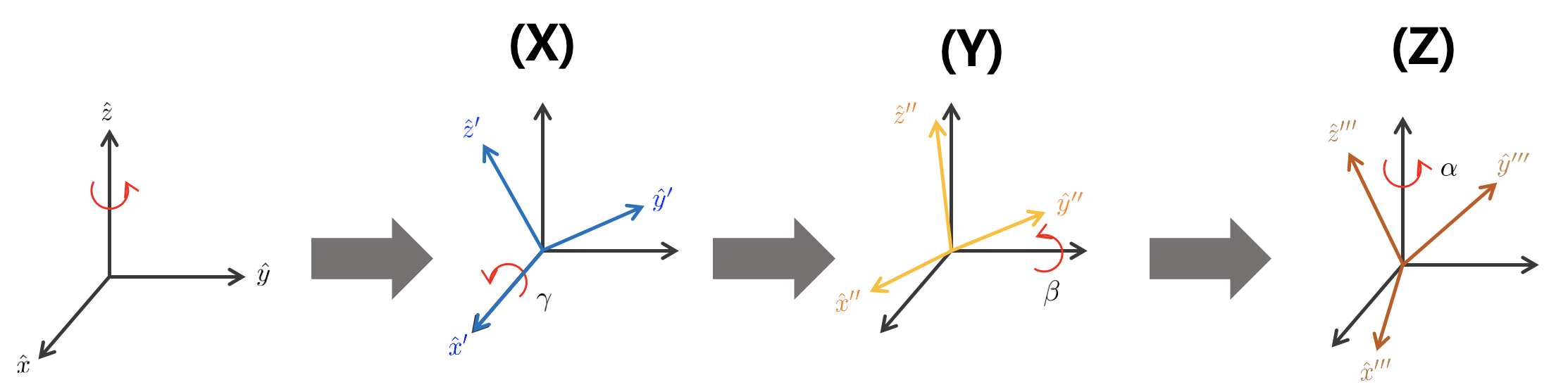
위와 같이 $x,y,z$ 축 순서대로 회전하는 경우 새로운 축은 아래 공식과 같이 나타낼 수 있다.
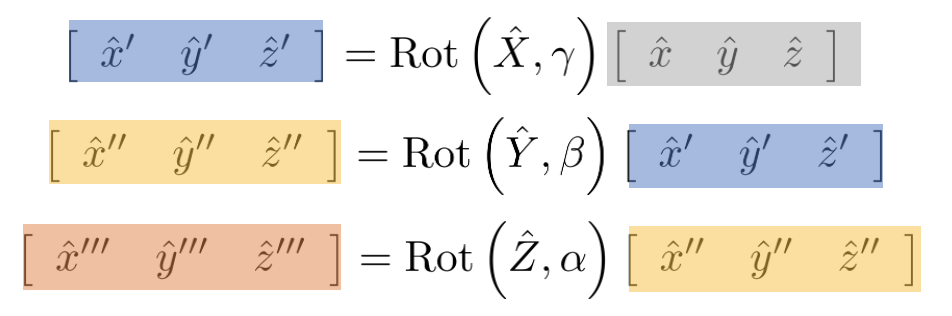
이를 한번에 정리하면 아래와 같다. 이 때 $\alpha, \beta, \gamma$를 각각 yaw, pitch, roll라고 한다.
\begin{equation}
\begin{aligned}
\left[\begin{array}{ccc}\hat{x}^{\prime\prime\prime} & \hat{y}^{\prime\prime\prime } & \hat{z}^{\prime\prime\prime } \end{array}\right] = \text{Rot}\left(\hat{Z},\alpha\right) \text{Rot}\left(\hat{Y},\beta\right)\text{Rot}\left(\hat{X},\gamma\right) \left[\begin{array}{ccc}\hat{x} & \hat{y} & \hat{z}\end{array}\right]
\end{aligned}
\end{equation}
위 식은 (\ref{eq:euler1})식과 동일하다. 따라서 고정 각도 표현법의 XYZ 회전은 오일러 각도 표현법의 ZXY와 동일한 회전을 의미한다.
Angle-axis representation
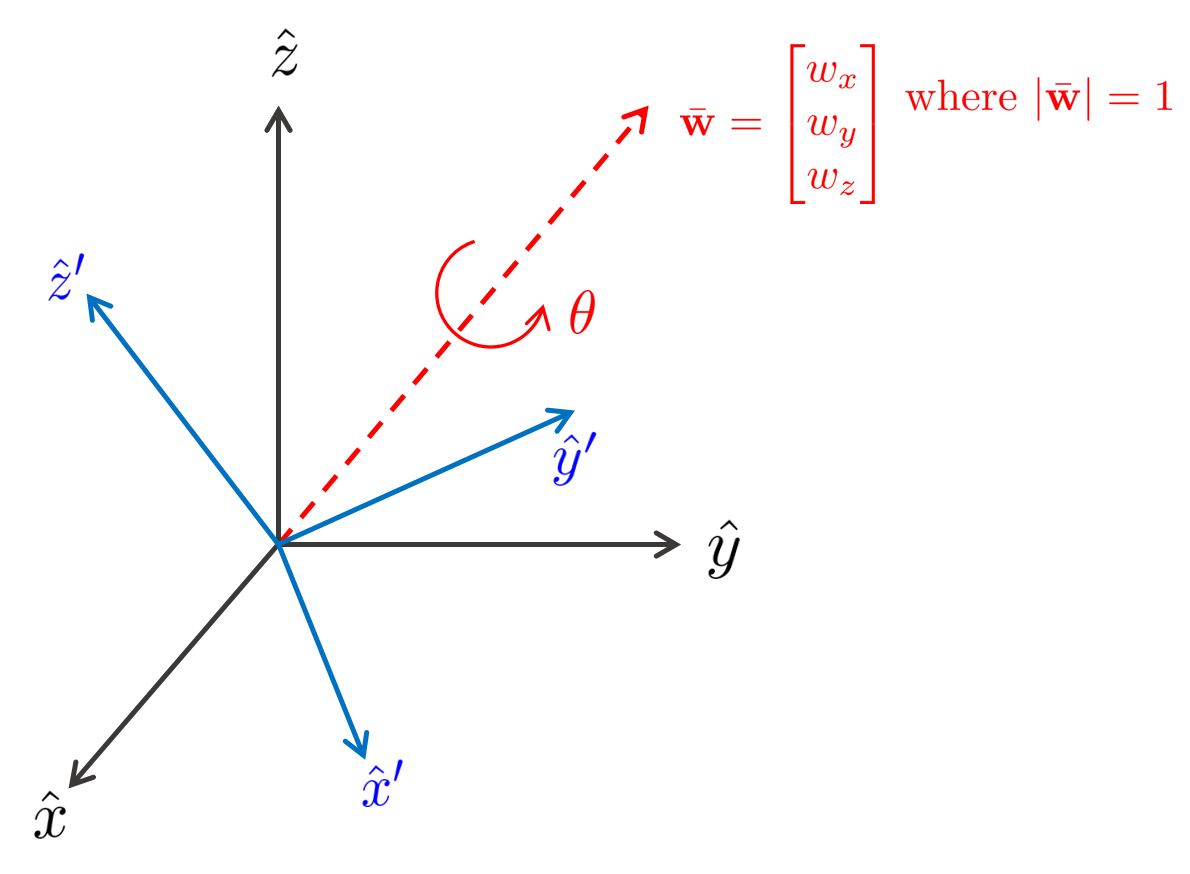
Angle-axis 표현법은 회전을 하나의 축(axis)과 이를 기준으로 회전한 각도(angle)로 표현하는 방법을 말한다. Angle-axis 표현법은 회전 축 $[x_{k} \ y_{k} \ z_{k}]$ 3개와 회전 각도 $\theta$ 1개의 파라미터를 사용하여 총 4개의 파라미터로 회전을 표현할 수 있다.
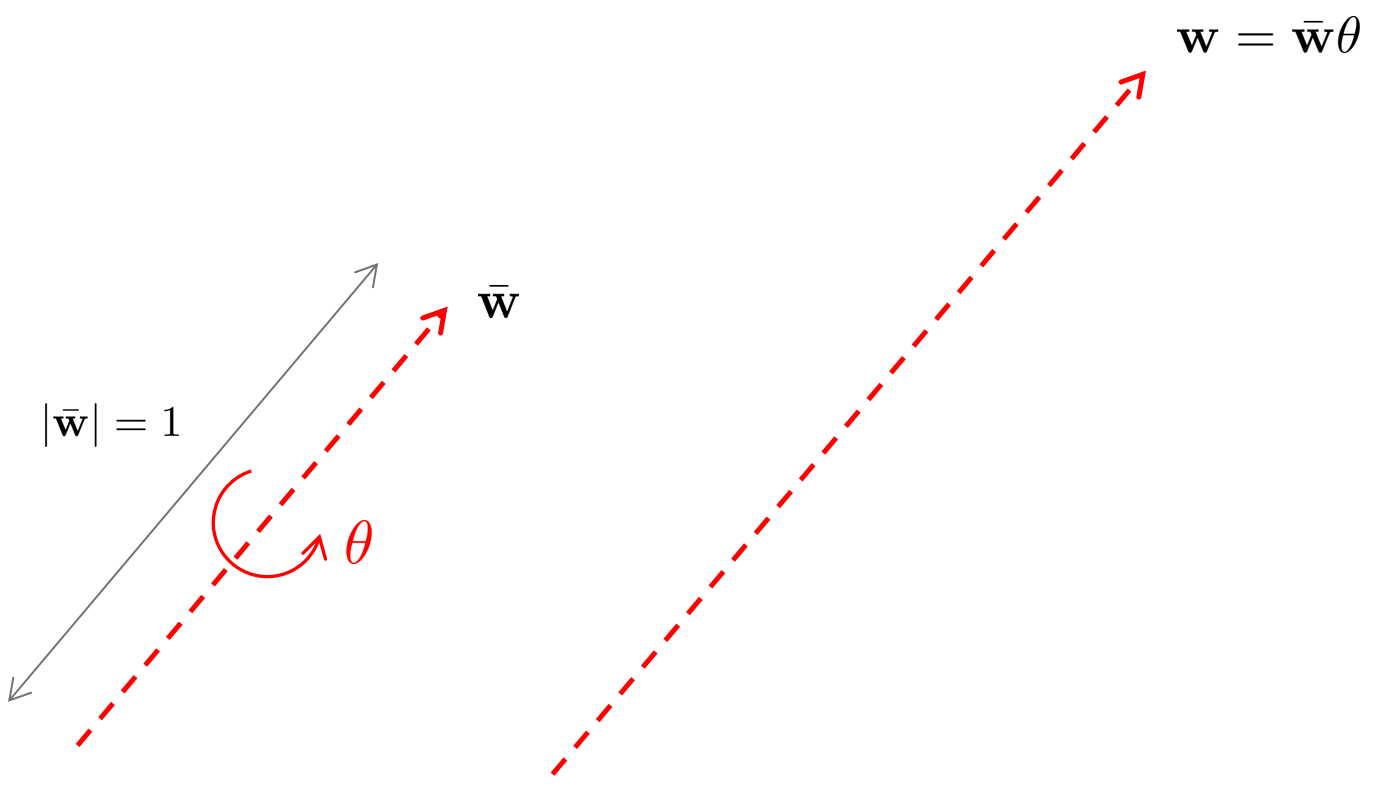
4개의 파라미터를 합치면 하나의 벡터로 표현할 수 있다. 이는 회전 벡터(rotation vector), rodrigues 파라미터, 각속도(angular velocity) 벡터 등으로 불린다.
\begin{equation}
\begin{aligned}
\mathbf{K} = \mathbf{\hat{K}}\theta = \begin{bmatrix}
x_{k}\theta\\
y_{k}\theta\\
z_{k}\theta
\end{bmatrix}
\end{aligned}
\end{equation}
Properties of angle-axis representation
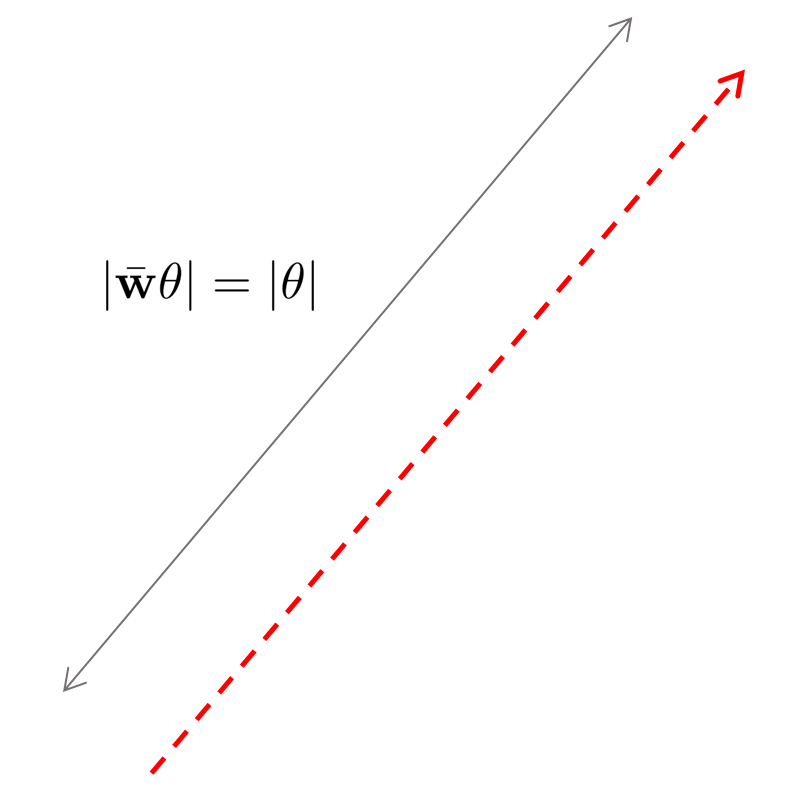
- Redundancy: 3차원 물체의 회전을 표현하기 위한 최소한의 파라미터는 3개이지만 angle-axis 표현법은 파라미터가 4개가 필요하다. 이는 3dof를 4dof로 표현한 셈이 되므로 angle-axis 표현법은 redundancy를 갖는다. 이러한 redundancy는 회전 벡터의 크기를 의미한다. 이 때, 회전 벡터 $\bar{\mathbf{w}}$의 크기 $|\bar{\mathbf{w}}|$를 정규화(normalize)하게 되면 $\bar{\mathbf{w}}$는 1dof를 잃게 되고 따라서 redundancy를 제거할 수 있다.
- 오일러 각도 표현법에서 발생한 gimbal lock 문제가 발생하지 않는다.
- 두 개의 회전 사이를 보간하는 경우 회전이 부드럽지 못한 문제가 존재한다.
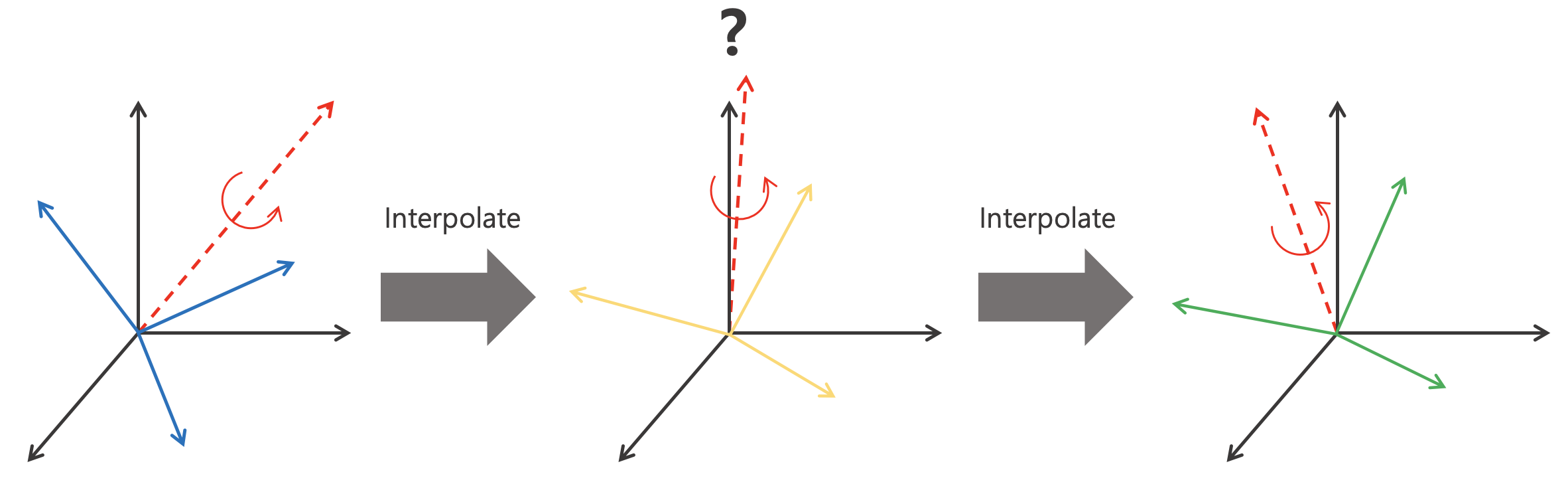
- 하나에 회전에 대하여 회전 벡터가 유일하지 않다는 문제를 가지고 있다.
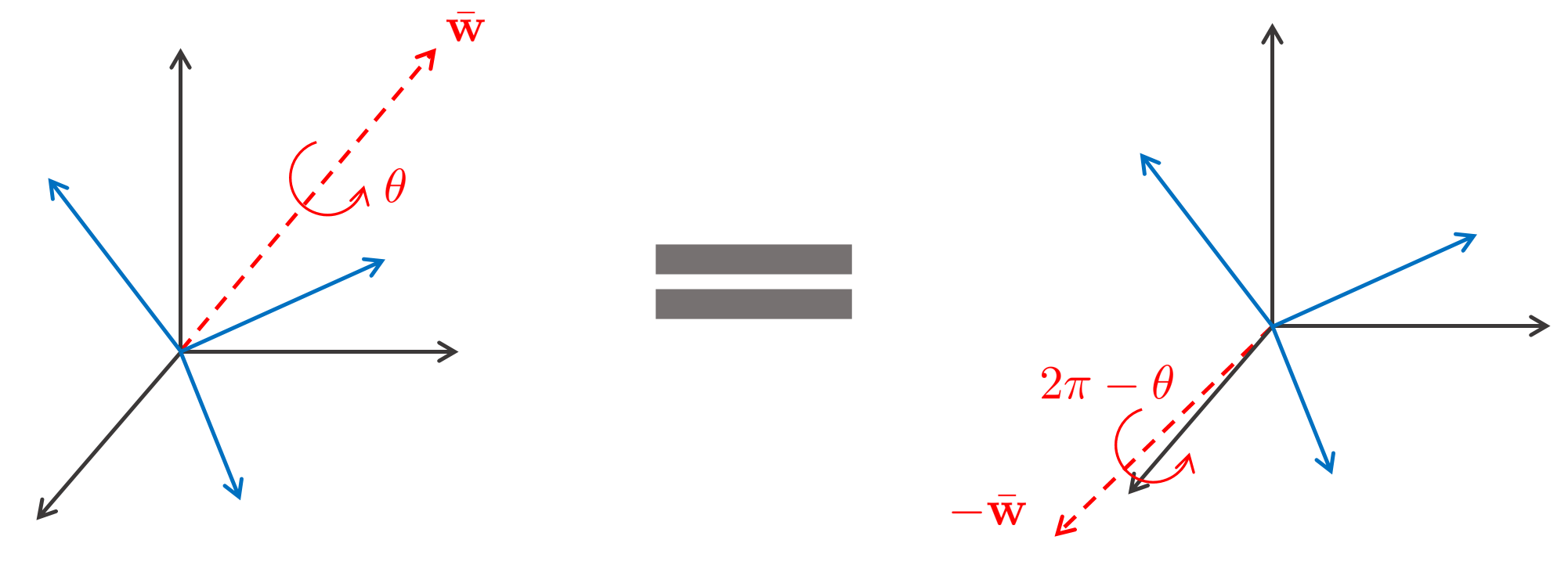
Quaternion
쿼터니언(quaternion)은 4개의 값으로 이뤄진 복소수 체계이다. 쿼터니언 자체는 회전과 관련없는 독립적인 복소수 체계이지만 이 중 단위 쿼터니언(unit quaternion)이 3차원 공간 상의 물체의 회전을 표현하는 연산자로 사용된다. 이는 컴퓨터 3D 그래픽스 분야에서 광범위하게 사용되며 실제로 회전 표현에 있어서 가장 효과적인 방법이다. 쿼터니언를 사용하면 다양한 회전 표현들의 문제점들을 회피할 수 있다.
- gimbal lock 현상이 발생하지 않는다.
- 행렬보다 점유 메모리 영역이 작고 계산부하도 낮다.
- 임의의 회전 벡터(angle-axis)를 손쉽게 쿼터니언으로 변환할 수 있다.
- 회전을 간단하게 합성할 수 있고 오차도 거의 발생하지 않는다.
- 두 개의 회전 사이의 보간을 매끄럽게 수행할 수 있다.
하지만 4차원 복소수이므로 시각화가 되지 않아 직관적으로 이해하기 어렵다는 단점이 존재한다. 쿼터니언는 다음과 같이 실수 $w$와 허수 $i,j,k$와 대응하는 $x,y,z$ 값으로 구성되어 있다.
\begin{equation}
\begin{aligned}
\mathbf{q} &= [w \ x\ y\ z]^{\intercal} \\
&= w + xi + yj + zk
\end{aligned}
\end{equation}
위와 같이 $[w \ x \ y \ z]$ 순서로 표현하고 $ijk=-1$을 만족하는 오른손 법칙을 따르는 쿼터니언 표기법을 'hamilton' 쿼터니언이라고도 부른다. 이와 반대로 $[x\ y\ z\ w]$로 표현하고 왼손 법칙을 따르는 쿼터니언을 'JPL' 쿼터니언이라고도 부른다. 이에 대한 자세한 내용은 Quaternion kinematics for the error-state Kalman filter 내용 정리 포스팅을 참고하면 된다. 본 섹션에서는 hamilton 쿼터니언 표기법으로 설명한다.
Properties of quaternion
- Addition: 두 쿼터니언의 덧셈은 실수부와 허수부를 나눠서 수행한다.
\begin{equation}
\begin{aligned}
\mathbf{p} + \mathbf{q} = \begin{bmatrix}
p_{w} \\ \mathbf{p}_{v}
\end{bmatrix} \pm \begin{bmatrix}
q_{w} \\ \mathbf{q}_{v}
\end{bmatrix} = \begin{bmatrix}
p_{w} \pm q_{w} \\ \mathbf{p}_{v} \pm \mathbf{q}_{w}
\end{bmatrix}
\end{aligned}
\end{equation} - Multiplication: 두 hamilton 쿼터니언의 곱은 $\otimes$로 표기하며 아래와 같다.
\begin{equation}
\begin{aligned}
\mathbf{p} \otimes \mathbf{q} =
\begin{bmatrix}
p_{w}q_{w} - p_{x}q_{x} - p_{y}q_{y} - p_{z}p_{z} \\
p_{w}q_{x} + p_{x}q_{w} + p_{y}q_{z} - p_{z}p_{y} \\
p_{w}q_{y} - p_{x}q_{z} + p_{y}q_{w} + p_{z}p_{x} \\
p_{w}q_{z} + p_{x}q_{y} - p_{y}q_{x} + p_{z}p_{w}
\end{bmatrix}\\
\end{aligned}
\end{equation} - Identity: 항등 쿼터니언(identity quaternion) $\mathbf{q}_{1}$은 다음과 같은 공식
$\mathbf{q}_{1}\otimes\mathbf{q} = \mathbf{q}\otimes\mathbf{q}_{1} = \mathbf{q}$를 만족하며 다음과 같이 정의된다.
\begin{equation}
\begin{aligned}
\mathbf{q}_{1} = 1 = \begin{bmatrix}
1 \\ \mathbf{0}_{v}
\end{bmatrix}
\end{aligned}
\end{equation} - Conjugate: 쿼터니언의 켤레복소수는 다음과 같이 정의된다.
\begin{equation}
\begin{aligned}
\mathbf{q}^{*} \triangleq q_{w} - \mathbf{q}_{v} = \begin{bmatrix}
q_{w} \\ -\mathbf{q}_{v}
\end{bmatrix}
\end{aligned}
\end{equation} - Norm: 쿼터니언의 놈은 다음과 같이 정의된다.
\begin{equation}
\begin{aligned}
\left \| \mathbf{q} \right \| \triangleq \sqrt{\mathbf{q} \otimes \mathbf{q}^{*}} = \sqrt{\mathbf{q}^{*} \otimes \mathbf{q}} = \sqrt{q_{w}^{2} + q_{x}^{2}+q_{y}^{2} +q_{z}^{2}} \in \mathbb{R}
\end{aligned}
\end{equation} - Inverse: 쿼터니언의 역은 $\mathbf{q}^{-1}$과 같이 표기하며 다음과 같은 특성을 지닌다.
\begin{equation}
\begin{aligned}
\mathbf{q} \otimes \mathbf{q}^{-1} = \mathbf{q}^{-1} \otimes \mathbf{q} = \mathbf{q}_{1}
\end{aligned}
\end{equation} - Unit quaternion: 단위 쿼터니언은 $\left \| \mathbf{q} \right \| = 1$의 성질을 지닌다. 따라서 아래와 같은 특성을 만족한다.
\begin{equation}
\begin{aligned}
\mathbf{q}^{-1} = \mathbf{q}^{*}
\end{aligned}
\end{equation}
단위 쿼터니언은 3차원 공간에서 물체의 방향을 표현하거나 회전을 수행하는 연산자로써 사용된다. 위 성질은 역방향 회전이 기존 벡터에 켤레복소수 쿼터니언을 곱함으로써 얻어질 수 있다는 것을 의미한다. 단위 쿼터니언은 항상 다음과 같이 표현될 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{q} = \begin{bmatrix}
\cos\theta \\ \mathbf{u}\sin\theta
\end{bmatrix}
\end{aligned}
\end{equation}
이 때, $\mathbf{u} = u_{x}i + u_{y}j + u_{z}k$는 단위 벡터이며 $\theta$는 스칼라 값이다. $\mathbf{u}, \theta$는 angle-axis로 표현한 회전 벡터 파라미터를 의미하므로 angle-axis 표현법과 쿼터니언이 쉽게 상호 변환할 수 있음을 알 수 있다. - Pure quaternion: 실수부 $w=0$이고 허수부는 0이 아닐 때 이를 순수 쿼터니언(pure quaternion)이라고 한다.
\begin{equation}
\begin{aligned}
\mathbf{q} = [0\ x\ y \ z]^{\intercal}
\end{aligned}
\end{equation}
Unit quaternion as a rotation operator
단위 쿼터니언이 임의의 3차원 공간 상의 벡터 $\mathbf{x}$를 회전시키려면 다음과 같이 연산이 수행되어야 한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{x}'= \mathbf{q} \otimes \mathbf{x} \otimes \mathbf{q}^{*}
\end{aligned} }
\end{equation}
이 때, $\mathbf{x}$는 순수 쿼터니언(pure quaternion) 형태로 허수부에 3차원 벡터의 원소가 들어간다. 실수부 $w$는 0으로 설정한다. 쿼터니언 회전을 엄밀하게 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} 0 \\ \mathbf{x}' \end{bmatrix}= \mathbf{q} \otimes \begin{bmatrix} 0 \\\mathbf{x} \end{bmatrix} \otimes \mathbf{q}^{*}
\end{aligned}
\end{equation}
Interpolation
쿼터니언은 두 회전 사이의 보간(interpolation)을 가장 효과적으로 표현할 수 있다. 보간 방법의 종류는 다음과 같다.
- Linear Interpolation (LERP)
- Spherical Linear Interpolation (SLERP)
- Spherical Cubic Interpolation (SQUAD)
이를 비교한 그림은 다음과 같다. 쿼터니언 보간에 대해 보다 자세히 알고 싶으면 위키피디아를 참조하면 된다.
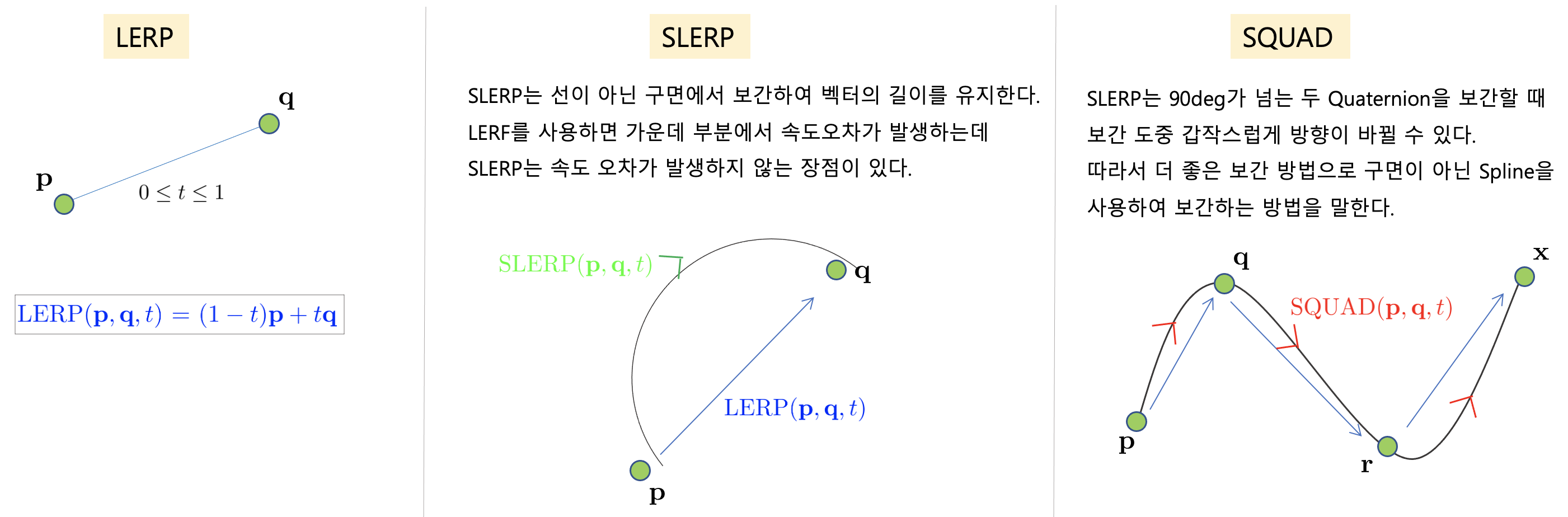
Relationship between rotation representations
지금까지 설명한 회전 행렬(9), 오일러 각도(3), 고정 각도(3), angle-axis(4), 쿼터니언(4) 표현 방법은 모두 3차원 공간 상의 회전을 표현하는 방법이다. 이러한 회전 표현법 사이에는 서로 변환이 가능하다.

Angle-axis and quaternion
Angle-axis $\mathbf{w} = \bar{\mathbf{w}}\theta = \begin{bmatrix}
w_{x}\theta\\
w_{y}\theta\\
w_{z}\theta
\end{bmatrix}$가 주어졌을 때 쿼터니언은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{w} = \bar{\mathbf{w}}\theta = \begin{bmatrix}
w_{x}\theta\\
w_{y}\theta\\
w_{z}\theta
\end{bmatrix} \quad \rightarrow \quad \mathbf{q} & = \begin{bmatrix} \cos\frac{\theta}{2} \\ \bar{\mathbf{w}}\sin\frac{\theta}{2} \end{bmatrix}
\end{aligned} }
\end{equation}
이 때, 회전 축 $\bar{\mathbf{w}}$가 단위 벡터이면 쿼터니언도 단위 쿼터니언이 된다. 이와 반대로 쿼터니언 $\mathbf{q} = [w,x,y,z]^{\intercal}$이 주어졌을 때 angle-axis는 다음과 같이 구할 수 있다. $w$는 쿼터니언의 실수부이고 $w_x, w_y, w_z$는 angle-axis의 단위 벡터임에 유의한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{q} = \begin{bmatrix}
w \\ x \\ y \\ z
\end{bmatrix} \quad \rightarrow \quad \begin{pmatrix} s = \sqrt{x^2 + y^2 + z^2} \\
w_{x} = x /s \\ w_{y} = y /s \\ w_{z} = z /s \\ \theta = 2\cos^{-1}(w)
\end{pmatrix}
\end{aligned} }
\end{equation}
Rotation matrix and quaternion
회전 행렬 $\mathbf{R} =\left[\begin{array}{ccc}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{array}\right]$이 주어져 있을 때 쿼터니언은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{R} =\left[\begin{array}{ccc}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{array}\right] \quad \rightarrow \quad \mathbf{q} = \begin{bmatrix}
w = \frac{\sqrt{r_{11}+r_{22}+r_{33}+1}}{2} \\
x=\frac{r_{23}-r_{32}}{4w} \\
y=\frac{r_{31}-r_{13}}{4w} \\
z=\frac{r_{12}-r_{21}}{4w}
\end{bmatrix}
\end{aligned} }
\end{equation}
만약 $w=0$인 경우 위 식이 성립하지 않는다. 이런 경우에는 $w,x,y,z$ 중 가장 큰 값을 찾고 이를 통해 나머지 세 개의 값을 계산해야 한다. 이와 반대로 쿼터니언 $\mathbf{q} = [w,x,y,z]^{\intercal}$이 주어졌을 때 회전 행렬은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{q} = [w,x,y,z]^{\intercal} \quad \rightarrow \quad \mathbf{R} = \begin{bmatrix}
x^{2}+y_{2}-z^{2}+w^{2} & 2xy-2wz & 2xz+2wy \\
2xy+2wz & -x^{2}+y_{2}-z^{2}+w^{2} & 2yz-2wx \\
2xz-2wy & 2yz+2wx & -x^{2}-y_{2}+z^{2}+w^{2}
\end{bmatrix}
\end{aligned} }
\end{equation}
Rotation matrix and angle-axis
회전 행렬 $\mathbf{R} =\left[\begin{array}{ccc}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{array}\right]$이 주어져 있을 때 angle-axis은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{R} =\left[\begin{array}{ccc}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{array}\right] \quad \rightarrow \quad \begin{pmatrix}
\theta = \text{arccos}(\frac{r_{11}+r_{22}+r_{33}-1}{2}) \\
\bar{\mathbf{w}} = \frac{1}{2\sin\theta}\begin{bmatrix}
r_{32}-r_{23} \\
r_{13}-r_{31} \\
r_{21}-r_{12}
\end{bmatrix}
\end{pmatrix}
\end{aligned}}
\end{equation}
이와 반대로 angle-axis $\mathbf{w} = \bar{\mathbf{w}}\theta = \begin{bmatrix}
w_{x}\theta\\
w_{y}\theta\\
w_{z}\theta
\end{bmatrix}$가 주어졌을 때 회전 행렬은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{w} = \bar{\mathbf{w}}\theta = \begin{bmatrix}
w_{x}\theta\\
w_{y}\theta\\
w_{z}\theta
\end{bmatrix} \quad \rightarrow \quad \mathbf{R} = \begin{bmatrix}
w_{x}^{2}\text{v}\theta +\text{c}\theta & w_{x}w_{y}\text{v}\theta-w_{z}\text{s}\theta & w_{x}w_{z}\text{v}\theta+w_{y}\text{s}\theta \\
w_{x}w_{y}\text{v}\theta +w_{z}\text{s}\theta & w_{y}^{2}\text{v}\theta+\text{c}\theta & w_{y}w_{z}\text{v}\theta-w_{x}\text{s}\theta \\
w_{x}w_{z}\text{v}\theta -w_{y}\text{s}\theta & w_{y}w_{z}\text{v}\theta + w_{x}\text{s}\theta & w_{z}^{2}\text{v}\theta+\text{c}\theta
\end{bmatrix}
\end{aligned} }
\end{equation}
- $s\theta = \sin\theta$
- $c\theta = \cos\theta$
- $\text{v}\theta = 1 - \cos\theta$
위 식을 컴팩트하게 표현하면 아래와 같이 나타낼 수 있는데 이를 Rodrigues 공식이라고 한다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{w} = \bar{\mathbf{w}}\theta = \begin{bmatrix}
w_{x}\theta\\
w_{y}\theta\\
w_{z}\theta
\end{bmatrix} \quad \rightarrow \quad \mathbf{R} = \mathbf{I} + \sin\theta [\bar{\mathbf{w}}]_{\times} + (1 - \cos\theta)[\bar{\mathbf{w}}]^{2}_{\times}
\end{aligned} }
\end{equation}
Quaternion and euler angle(ZYX)
쿼터니언 $\mathbf{q} = [w,x,y,z]^{\intercal}$이 주어졌을 때 오일러 각도는 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\mathbf{q} = [w,x,y,z]^{\intercal} \quad \rightarrow \quad \begin{bmatrix}
\alpha\\
\beta\\
\gamma
\end{bmatrix}
=
\begin{bmatrix}
\text{arctan}\frac{2(wx+yz)}{1-2(x^{2}+y^{2})}\\
\text{arcsin}(2(wy-xz))\\
\text{arctan}\frac{2(wz+xy)}{1-2(y^{2}+z^{2})}
\end{bmatrix}
\end{aligned} }
\end{equation}
이와 반대로 오일러 각도 $\gamma,\beta,\alpha$가 주어져 있을 때 쿼터니언은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\text{Euler}_{ZYX}(\alpha,\beta,\gamma) \quad \rightarrow \quad x = \sin\frac{\beta}{2}\cos\frac{\alpha-\gamma}{2} \\
y = \sin\frac{\beta}{2}\sin\frac{\alpha-\gamma}{2} \\
z = \cos\frac{\beta}{2}\sin\frac{\alpha+\gamma}{2} \\
w = \sin\frac{\beta}{2}\cos\frac{\alpha+\gamma}{2}
\end{aligned} }
\end{equation}
Rotation matrix and euler angle(ZYX)
오일러 각도 $\gamma,\beta,\alpha$가 주어져 있을 때 회전 행렬은 다음과 같이 구할 수 있다.
\begin{equation}
\boxed{ \begin{aligned}
\text{Euler}_{ZYX}(\alpha,\beta,\gamma) \quad \rightarrow \quad \mathbf{R} = \begin{bmatrix}
c_{\alpha}c_{\beta} & c_{\alpha}s_{\beta}s_{\gamma}-s_{\alpha}c_{\gamma} & c_{\alpha}s_{\beta}c_{\gamma}+s_{\alpha}s_{\gamma} \\
s_{\alpha}c_{\beta} & s_{\alpha}s_{\beta}s_{\gamma}+c_{\alpha}c_{\gamma} & s_{\alpha}s_{\beta}c_{\gamma}-c_{\alpha}s_{\gamma}\\
-s_{\beta} & c_{\beta}s_{\gamma} & c_{\beta}c_{\gamma}
\end{bmatrix}
\end{aligned} }
\end{equation}
- $s_\alpha = \sin\alpha$
- $c_\alpha = \cos\alpha$
이와 반대로 회전 행렬이 주어졌을 때 오일러 각도를 구하는 공식은 수식이 매우 길고 복잡하며 잘 사용하지 않기 때문에 생략한다. 자세한 내용은 해당 링크를 참조하면 된다.
References
'Fundamental' 카테고리의 다른 글
| 확률 이론(Probability Theory) 개념 정리 Part 1 - Probability, Random Variable, Distribution (1) | 2023.11.13 |
|---|---|
| [SLAM] Hand-eye Calibration 개념 정리 (+ Trajectory Evaluation) (1) | 2023.11.10 |
| [SLAM] 에러와 자코비안 정리(Errors and Jacobians) 정리 Part 2 (0) | 2023.01.13 |
| [SLAM] 에러와 자코비안 정리(Errors and Jacobians) 정리 Part 1 (15) | 2023.01.08 |
| Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 3 (6) | 2022.10.10 |
 A L I D A
A L I D A





