Youtube
다중관점기하학(Multiple View Geometry) 개념 정리
www.youtube.com
1. Epipolar Geometry and the Fundamental Matrix
1.1. Epipolar geometry

Epipolar geometry는 2개의 카메라 이미지 사이에 정의되는 기하학 관계 를 의미한다. 이는 3차원 물체의 구조와는 독립적이며 오로지 카메라의 내부 파라미터와 두 카메라 사이의 상대 포즈에만 의존한다. 위 그림과 같이 3차원 공간 상에 두 카메라의 중심점 $\mathbf{C}, \mathbf{C}^{\prime}$과 점 $\mathbf{X}$가 주어졌을 때 세 점을 통해 유일하게 결정되는 평면을 Epipolar Plane $\pi$ 라고 한다. 또한 카메라의 중심점 $\mathbf{C}$를 $\mathbf{P}^{\prime}$을 통해 프로젝션한 점 $\mathbf{P}^{\prime}\mathbf{C}=\mathbf{e}^{\prime}$을 이미지 평면 $\pi_{\mathbf{C}^{\prime}}$의 Epipole $\mathbf{e}^{\prime}$이라고 한다. 그리고 $\mathbf{e}^{\prime}$과 $\mathbf{x}^{\prime}$을 잇는 직선을 Epipolar Line $\mathbf{l}^{\prime}$이라고 한다. $\mathbf{e}, \mathbf{l}$ 또한 마찬가지로 이미지 평면 $\pi_{\mathbf{C}}$의 Epipole과 Epipolar Line을 의미한다.
1.2. The fundamental matrix $\mathbf{F}$
Fundamental Matrix는 2개의 주어진 카메라의 중심점 $\mathbf{C}, \mathbf{C}^{\prime}$이 주어질 때 $\mathbf{F} \in \mathbb{R}^{3\times 3}$이며 rank 2를 가지는 행렬 을 의미한다. $\mathbf{F}$는 두 카메라의 이미지 평면에 있는 점들의 대응쌍 $\mathbf{x}, \mathbf{x}^{\prime}$에 대하여
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime\intercal}\mathbf{Fx} = 0
\end{aligned}
\end{equation}
을 만족한다. 이 때 곱해지는 순서에 따라 의미가 달라지며 $\mathbf{x}^{\prime\intercal}\mathbf{Fx}=0$인 경우 두 카메라 $\mathbf{C},\mathbf{C}^{\prime}$ 사이의 Fundamental Matrix라고 하고 $\mathbf{x}^{\intercal}\mathbf{F}^{\prime}\mathbf{x}^{\prime}=0$인 경우 두 카메라 $\mathbf{C}^{\prime},\mathbf{C}$ 사이의 Fundamental Matrix라고 한다. 이 때, $\mathbf{F}^{\intercal} = \mathbf{F}^{\prime}$ 관계가 성립한다.
기하학적 측면에서 보면, $\mathbf{x}^{\prime\intercal}\mathbf{Fx}=0$에서 $\mathbf{Fx}$는 카메라 $\mathbf{C}$의 이미지 평면 $\pi_{\mathbf{C}}$ 위의 점 $\mathbf{x}$가 존재할 때 이와 상응하는 Epipolar Line $\mathbf{l}^{\prime} \in \pi_{\mathbf{C}^{\prime}}$을 의미한다. 따라서 $\mathbf{F}$는 이미지 평면 $\pi_{\mathbf{C}}$ 위의 점 $\mathbf{x}$를 Epipolar Line $\mathbf{l}^{\prime}$으로 매핑하는 함수로 생각할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{F}: \ \mathbf{x} \mapsto \mathbf{l}^{\prime} \\
& \text{where, } \ \ \mathbf{x} \in \pi_{\mathbf{C}} \in \mathbb{P}^{2} \\
& \mathbf{l}^{\prime} \in (\mathbb{P}^{2})^{\vee}
\end{aligned}
\end{equation}
1.2.1. Proof
($\Rightarrow$)$\mathbf{l}^{\prime} = \mathbf{Fx}$인 경우 Epipolar Line $\mathbf{l}^{\prime}$에 위치한 점 $\mathbf{x}^{\prime}$에 대하여 다음이 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime\intercal}\mathbf{l}^{\prime} = \mathbf{x}^{\prime\intercal}\mathbf{Fx}=0 \quad \forall \mathbf{x} \leftrightarrow \mathbf{x}^{\prime}
\end{aligned}
\end{equation}
($\Leftarrow$) 이미지 평면 $\pi_{\mathbf{C}}$ 위의 점 $\mathbf{x}$를 Back-projection하여 $\mathbf{X}_{1}, \mathbf{X}_{2}$ 점이 생성되었다고 했을 때, 이를 $\pi_{\mathbf{C}^{\prime}}$에 프로젝션시키면 각각 $\mathbf{x}^{\prime}_{1} = \mathbf{P}^{\prime}\mathbf{X}_{1}$, $\mathbf{x}^{\prime}_{2} = \mathbf{P}^{\prime}\mathbf{X}_{2}$ 점들이 생성된다. 이 때 Fundamental Matrix $\mathbf{F}$에 의해
\begin{equation}
\begin{aligned}
& \mathbf{x}^{\prime\intercal}_{1}\mathbf{Fx} = 0 \\
& \mathbf{x}^{\prime\intercal}_{2}\mathbf{Fx} = 0
\end{aligned}
\end{equation}
의 관계가 성립하므로 $\mathbf{Fx}$는 $\mathbf{x}^{\prime\intercal}_{i}, \ i=1,2$와 수직인 Epipolar Line $\mathbf{l}^{\prime}$을 의미한다.
1.2.2. Geometric derivation

두 카메라 $\mathbf{C}, \mathbf{C}^{\prime}$가 있을 때 이미지 평면 $\pi_{\mathbf{C}}$ 위의 점 $\mathbf{x}$를 Back-projection한 직선 $\mathbf{l}_{\mathbf{x}}$가 3차원 공간 상에서 임의의 평면 $\pi_{0}$와 한 점에서 만난다고 가정한다. 이 때 $\mathbf{C}, \mathbf{C}^{\prime}$의 이미지 점들을 연결해주는 Homography $\mathbf{H}_{\pi_{0}}$를 생각해보면
\begin{equation}
\begin{aligned}
\mathbf{H}_{\pi_{0}} : & \pi_{\mathbf{C}} \mapsto \pi_{\mathbf{C}^{\prime}} \\
& \mathbf{x} \mapsto \mathbf{x}^{\prime} \\
& \mathbf{x} \mapsto \mathbf{P}^{\prime}(\mathbf{l_{x}} \cap \pi_{0})
\end{aligned}
\end{equation}
$\pi_{\mathbf{C}^{\prime}}$ 위에 프로젝션된 점을 $\mathbf{x}^{\prime} = \mathbf{P}^{\prime}(\mathbf{l}_{\mathbf{x}} \cap \pi_{0})$라고 하고 Epipolar Line $\mathbf{l}^{\prime}$을 $\mathbf{x}^{\prime}$와 Epipole $\mathbf{e}^{\prime}$를 이어주는 직선이라고 정의하면
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime} \times \mathbf{x}^{\prime} & = \mathbf{e}^{\prime \wedge}\mathbf{x}^{\prime} \\
& = \mathbf{e}^{\prime\wedge} \mathbf{H}_{\pi_{0}}(\mathbf{x}) \quad \text{is Epipolar Line.}
\end{aligned}
\end{equation}
와 같이 나타낼 수 있다. 이 때 $\mathbf{l}^{\prime} = \mathbf{Fx}$의 공식을 사용하면
\begin{equation}
\begin{aligned}
\mathbf{l}^{\prime} & = \mathbf{Fx} \\
& = \mathbf{e}^{\prime\wedge} \mathbf{H}_{\pi_{0}} \mathbf{x} \\
\end{aligned}
\end{equation}
과 같다. 따라서 $\mathbf{F} = \mathbf{e}^{\prime\wedge}\mathbf{H}_{\pi_{0}}$ 가 성립한다. 이 때, $\mathbf{H}_{\pi_{0}}$는 rank 3인 행렬이며 $\mathbf{e}^{\prime\wedge}$는 rank 2인 행렬이므로 $\mathbf{F}$는 rank 2인 행렬이 된다.
1.2.3. Algebraic derivation
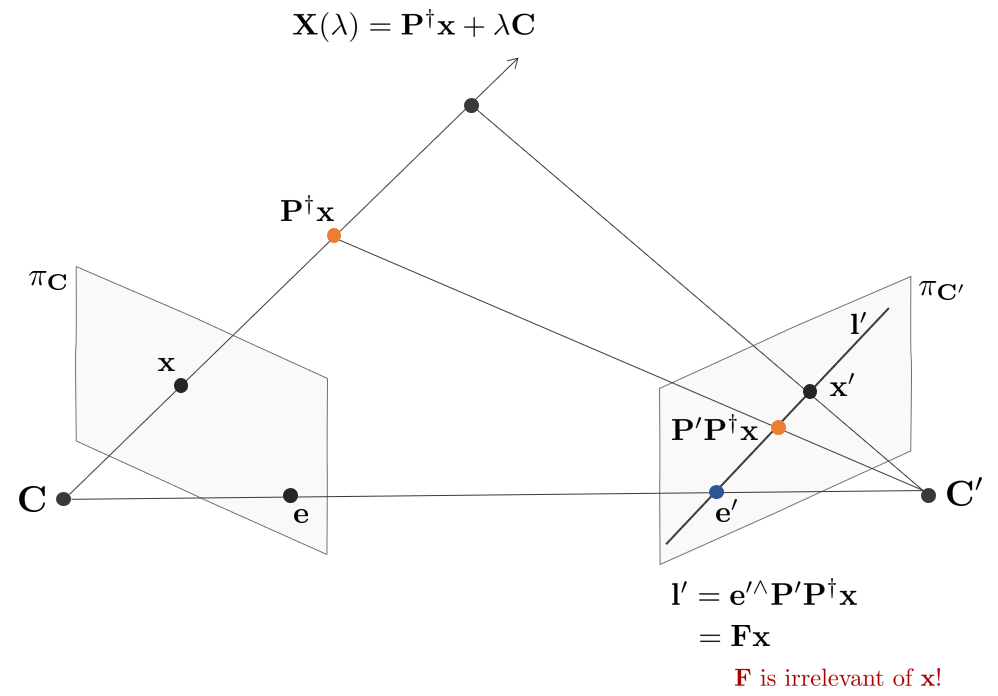
Epipolar Line $\mathbf{l}^{\prime} = \mathbf{P}^{\prime}(\mathbf{X(\lambda)})$와 같다. 이 때 $\mathbf{X}(\lambda)$는 카메라 $\mathbf{C}$의 중심점을 지나는 $\mathbf{x}$의 Back-projection 직선을 의미한다. $\mathbf{X}(\lambda)$는 다음과 같이 다시 작성할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{X}(\lambda) = \mathbf{P}^{\dagger}\mathbf{x} + \lambda \mathbf{C} \quad \lambda \in \mathbb{R}\\
\end{aligned}
\end{equation}
여기서 $\mathbf{P}^{\dagger}$는 $\mathbf{P}$의 Pseudo Inverse를 의미하고
\begin{equation}
\begin{aligned}
\mathbf{P}^{\dagger} = \mathbf{P}^{\intercal}(\mathbf{PP}^{\intercal})^{-1}
\end{aligned}
\end{equation}
이 때, $\mathbf{l}^{\prime} = \mathbf{P}^{\prime}(\mathbf{X}(\lambda))$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{P}^{\prime}(\mathbf{X}(\lambda)) & = \mathbf{P}^{\prime}\mathbf{P}^{\dagger}\mathbf{x} + \lambda \mathbf{P}^{\prime}\mathbf{C} \\
& \mathbf{P}^{\prime}\mathbf{P}^{\dagger}\mathbf{x} + \lambda \mathbf{e}^{\prime}
\end{aligned}
\end{equation}
$\mathbf{P}^{\prime}\mathbf{C}$는 카메라 $\mathbf{C}$의 중심점을 $\pi_{\mathbf{C}^{\prime}}$에 프로젝션시킨 점을 의미하므로 Epipole $\mathbf{e}^{\prime}$가 된다. $\lambda=0$일 때 $\mathbf{P}^{\prime}(\mathbf{X}(0))= \mathbf{P}^{\prime}\mathbf{P}^{\dagger}\mathbf{x}$이고 $\lambda=\infty$일 때 $\mathbf{P}^{\prime}(\mathbf{X}(\infty))=\mathbf{P}^{\prime}\mathbf{C}=\mathbf{e}^{\prime}$가 된다. 따라서 Epipolar Line $\mathbf{l}^{\prime}$는 두 점을 잇는 직선이므로
\begin{equation}
\begin{aligned}
\mathbf{l}^{\prime} & = \mathbf{e}^{\prime\wedge} \mathbf{P}^{\prime}\mathbf{P}^{\dagger}\mathbf{x} \\
& = \mathbf{F}\mathbf{x} \\
\therefore \mathbf{F} & = \mathbf{e}^{\prime\wedge} \mathbf{P}^{\prime}\mathbf{P}^{\dagger}
\end{aligned}
\end{equation}
이 된다. 추가적으로 Epipole $\mathbf{e}^{\prime}$는 Epipolar Line $\mathbf{l}^{\prime}$에 포함되어 있고 모든 $\mathbf{x}_{i}$에 대해
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime \intercal} \mathbf{Fx}_{i} = (\mathbf{e}^{\prime \intercal}\mathbf{F}) \mathbf{x}_{i} = 0 \quad \forall \mathbf{x}_{i}
\end{aligned}
\end{equation}
이 성립하므로 $\mathbf{e}^{\prime \intercal}\mathbf{F}=0$이 성립한다. 결론적으로 $\mathbf{e}^{\prime}$는 $\mathbf{F}$의 Left null vector 이다. 또한 $\mathbf{e}$는 $\mathbf{F}$의 (right) null vector가 된다.
1.2.4. Properties of the fundamental matrix
Fundamental Matrix $\mathbf{F}$의 성질은 다음과 같다.
- Transpose: $\mathbf{F}$가 두 카메라 $(\mathbf{P}, \mathbf{P}')$에 대한 Fundamental Matrix라고 했을 때 $\mathbf{F}^{\intercal}$은 $(\mathbf{P}', \mathbf{P})$에 대한 Fundamental Matrix가 된다.
- Epipolar Lines: 첫번째 이미지의 대응점 $\mathbf{x}$에 대해 이와 상응하는 두번째 이미지의 Epipolar Line은 $\mathbf{l}' = \mathbf{Fx}$와 같이 나타낼 수 있다. 이와 유사하게 두번째 이미지의 대응점 $\mathbf{x}'$에 대해 이와 상응하는 첫번째 이미지의 Epipolar Line은 $\mathbf{l} = \mathbf{F}^{\intercal}\mathbf{x}'$와 같이 나타낼 수 있다.
- The Epipole: $\mathbf{e}$가 아닌 모든 점 $\mathbf{x}$에 대한 Epipolar Line $\mathbf{l}' = \mathbf{Fx}$는 항상 $\mathbf{e}'$를 지나간다. 따라서 $\mathbf{e}'$는 모든 $\mathbf{x}$에 대해 $\mathbf{e}'^{\intercal}(\mathbf{Fx}) = (\mathbf{e}'^{\intercal}\mathbf{F})\mathbf{x} = 0$가 성립한다. 이는 즉, $\mathbf{e}'^{\intercal}\mathbf{F} = 0$의 성질을 만족하므로 $\mathbf{e}'$는 $\mathbf{F}$의 Left null-vector가 된다. 이와 유사하게 $\mathbf{Fe}=0$에 따라 $\mathbf{e}$는 $\mathbf{F}$의 Right null-vector가 된다.
- Fundamental Matrix는 rank 2인 Homogeneous 행렬이며 7자유도(DOF)를 갖는다. 그리고 rank 2 행렬이므로 역행렬이 존재하지 않는다. 3x3 행렬의 마지막 원소는 Homogeneous 좌표계의 스케일 모호성(Scale Ambiguity)에 의해 1자유도를 하나 잃고 $\det \mathbf{F} = 0$ 제약조건에 의해 추가적으로 1자유도를 잃어서 7자유도를 가진다.
1.3. The epipolar line homography
두 카메라 $\mathbf{C}, \mathbf{C}^{\prime}$이 존재하고 이미지 평면 위의 한 점을 각각 $\mathbf{x}, \mathbf{x}^{\prime}$라고 하면 이에 상응하는 Epipolar Line $\mathbf{l}, \mathbf{l}^{\prime}$이 존재한다. 이 때, $\mathbf{l}$과 $\mathbf{l}^{\prime}$ 사이에는 별도의 대응 관계가 성립 하는데 이는
\begin{equation}
\begin{aligned}
\mathbb{P}(\pi)^{\vee} \mapsto \mathbb{P}(\pi^{\prime})^{\vee}
\end{aligned}
\end{equation}
매핑 관계인 Homography 행렬 로 주어진다.
1.3.1. Result 9.5
카메라 중심점 $\mathbf{C}$를 통과하면서 Epipole $\mathbf{e}$를 지나지 않는 직선 $\mathbf{k}$가 있을 때 $\mathbf{k}$는 Epipolar Line $\mathbf{l}$과 반드시 한 점 $\mathbf{p}$에서 만난다. $\mathbf{p}$는
\begin{equation}
\begin{aligned}
\mathbf{p} = \mathbf{k}^{\wedge}\mathbf{l}
\end{aligned}
\end{equation}
과 같이 구할 수 있고 $\mathbf{p}$는 Fundamental Matrix에 의해 Epipolar Line $\mathbf{l}^{\prime}$으로 프로젝션되므로
\begin{equation}
\begin{aligned}
\mathbf{l}^{\prime} & = \mathbf{F}\mathbf{k}^{\wedge}\mathbf{l} \\
& = \mathbf{H}\mathbf{l} \\
\end{aligned}
\end{equation}
의 관계가 성립한다. 따라서 $\mathbf{l}, \mathbf{l}^{\prime}$은 $\mathbf{H}=\mathbf{Fk}^{\wedge}$인 Homography 행렬에 의해 대응 관계가 성립 한다.
1.4. Fundamental matrices arising from special motions
1.4.1. Pure translation

순수 이동(pure translation)이란 카메라 센터를 회전하지 않고 이동만 하는 것을 의미한다. 이 때, 월드의 모든 물체를 고정시킨 채로 카메라를 움직이는 것과 카메라를 고정시킨 채로 월드의 모든 물체를 이동시키는 것은 동일하다. 처음 위치의 카메라 행렬과 카메라 센터를 각각 $\mathbf{P}, \mathbf{C}$라고 하고 순수 이동 후 카메라 행렬과 카메라 센터를 각각 $\mathbf{P}^{\prime}, \mathbf{C}^{\prime}$라고 할 때 두 카메라의 베이스라인의 길이는 카메라 중심점의 순수 이동량과 동일하다.
또한 두 카메라의 Epipole을 각각 $\mathbf{e},\mathbf{e}^{\prime}$이라고 하면 두 Epipole의 위치는 동일하며 이는 곧 소실점(vanishing point)을 의미한다.
\begin{equation}
\begin{aligned}
\mathbf{e} = \mathbf{e}^{\prime} = \mathbf{v}
\end{aligned}
\end{equation}
이러한 순수 이동 상황에서 $\mathbf{e}=\mathbf{e}^{\prime}$를 Auto Epipolar라고 한다.
대수적으로 Fundamental Matrix를 유도해보면 처음 카메라 행렬을 $\mathbf{P}=\mathbf{K}[\mathbf{I}|0]$이라고 하고 순수 이동 후 카메라 행렬을 $\mathbf{P}^{\prime}=\mathbf{K}[\mathbf{I}|\mathbf{t}]$라고 하면 이전 섹션에서 Fundamental Matrix $\mathbf{F}$는 $\mathbf{F} = \mathbf{e}^{\prime\wedge}\mathbf{P}^{\prime}\mathbf{P}^{\dagger}$ 이므로
\begin{equation}
\begin{aligned}
\mathbf{F} & = \mathbf{e}^{\prime\wedge}\mathbf{P}^{\prime}\mathbf{P}^{\dagger} \\
& = \mathbf{e}^{\prime\wedge}\mathbf{KK}^{-1} \\
& = \mathbf{e}^{\prime\wedge}
\end{aligned}
\end{equation}
따라서 순수 이동 상황에서 Fundamental Matrix는 $\mathbf{F}=\mathbf{e}^{\prime\wedge}$ 이다.
1.5. Retrieving the camera matrices
1.5.1. Projective invariance and canonical cameras
1.5.2. Result 9.8
두 카메라 $\mathbf{C}, \mathbf{C}^{\prime}$에 대응하는 이미지 평면 상의 점들 $\mathbf{x}, \mathbf{x}^{\prime}$과 Fundamental Matrix $\mathbf{F}$가 존재할 때 $\mathbf{F}$는 $\mathbf{x}\leftrightarrow \mathbf{x}^{\prime}$ 대응쌍의 Homography 변환에 상관없이 동일하다. 다시 말하면, $\mathbb{P}^{3} \mapsto \mathbb{P}^{3}$을 만족하는 Homograhpy 변환 $\mathbf{H} \in \mathbb{R}^{4\times 4}$가 존재할 때 $\mathbf{H}$는
\begin{equation}
\begin{aligned}
(\mathbf{P},\mathbf{P}^{\prime}) \mapsto (\mathbf{PH}, \mathbf{P}^{\prime}\mathbf{H})
\end{aligned}
\end{equation}
를 만족하는데 이러한 $\mathbf{H}$에 관계없이 Fundamental Matrix $\mathbf{F}$는 동일 하다.
1.5.3. Proof
$(\mathbf{PH},\mathbf{P}^{\prime}\mathbf{H})$에 해당하는 대응점쌍 $\mathbf{x}\leftrightarrow \mathbf{x}^{\prime}$에 대해서
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime\intercal}\tilde{\mathbf{F}}\mathbf{x} = 0
\end{aligned}
\end{equation}
이 성립한다. 이 때 $\mathbf{x}=\mathbf{PHX}, \mathbf{x}^{\prime}=\mathbf{P}^{\prime}\mathbf{HX}$이므로 이를 위 식에 대입하면
\begin{equation}
\begin{aligned}
\mathbf{X}^{\intercal}\mathbf{H}^{\intercal}\mathbf{P}^{\prime\intercal}\tilde{\mathbf{F}}\mathbf{PHX} = 0
\end{aligned}
\end{equation}
을 만족하고 위 식은 모든 $\forall \mathbf{X} \in \mathbb{P}^{3}$에 대해서 성립한다. $\mathbf{X}=\mathbf{H}^{-1}(\mathbf{HX}), \tilde{\mathbf{X}} = \mathbf{HX}$로 치환하여 다시 위 식에 대입하면
\begin{equation}
\begin{aligned}
& \tilde{\mathbf{X}}^{\intercal}\mathbf{H}^{-\intercal}\mathbf{H}^{\intercal}\mathbf{P}^{\prime\intercal}\tilde{\mathbf{F}}\mathbf{PHH}^{-1}\tilde{\mathbf{X}} = 0 \\
& \tilde{\mathbf{X}}^{\intercal}\mathbf{P}^{\prime\intercal}\tilde{\mathbf{F}}\mathbf{P}\tilde{\mathbf{X}} = 0 \\
& \tilde{\mathbf{x}}^{\prime\intercal}\tilde{\mathbf{F}}\tilde{\mathbf{x}} =0
\end{aligned}
\end{equation}
이 되어 결론적으로 $\mathbf{F} = \tilde{\mathbf{F}}$가 성립 한다.
1.5.4. Canonical form of camera matrices
위와 같은 성질에 따라 동일한 Fundamental Matrix $\mathbf{F}$에 여러 $(\mathbf{P},\mathbf{P}^{\prime})$ 쌍이 대응되므로 $\mathbf{F}$와 $(\mathbf{P},\mathbf{P}^{\prime})$는 One-to-Many Correspondence 관계가 된다. 따라서 이러한 모호성에도 불구하고 $\mathbf{F}$의 정확한 변환을 표현하기 위해 $\mathbf{P}=[\mathbf{I}|0]$, $\mathbf{P}^{\prime}=[\mathbf{M}|\mathbf{m}]$과 같이 처음 카메라 행렬 $\mathbf{P}$를 단순하게 나타내는 방법을 Canonical Form 이라고 한다. 하지만 $\mathbf{P}=[\mathbf{I}|0]$이라고 해서 $\mathbf{P}^{\prime}$이 유일하게 결정되는 것은 아니다.
임의의 카메라 행렬 $\mathbf{P} \in \mathbb{R}^{3\times4}$가 주어졌을 때 이를 역행렬이 존재하는 행렬 $\mathbf{P}^{\ast}=\begin{bmatrix} \mathbf{P} \\ \mathbf{r}_{4} \end{bmatrix} \in \mathbb{R}^{4\times4}$로 변경한 다음
\begin{equation}
\begin{aligned}
\mathbf{P}^{\ast}\mathbf{H} = \begin{bmatrix} \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{1} \end{bmatrix}
\end{aligned}
\end{equation}
을 만족하는 $\mathbf{H}$가 존재한다고 하면 $\mathbf{PH} = [\mathbf{I} | \mathbf{0}]$을 만족한다. 따라서 $\mathbf{H}$가 존재한다는 가정 하에 모든 임의의 카메라 행렬 $\mathbf{P}$는 Canonical Form으로 쓸 수 있다.
그렇다면 Fundamental Matrix $\mathbf{F}$는 $\mathbf{M}, \mathbf{m}$에 대하여 어떻게 쓸 수 있을까?
우선 임의의 두 카메라 행렬 $\mathbf{P} = \mathbf{K}[\mathbf{I}|0], \mathbf{P}^{\prime}=\mathbf{K}^{\prime}[\mathbf{R}|\mathbf{t}]$가 존재할 때 다음의 공식들이 성립한다.
\begin{equation}
\begin{aligned}
& \mathbf{PP}^{\intercal} = \mathbf{K}^{2} \\
& \mathbf{P}^{\dagger } = \mathbf{P}^{\intercal}(\mathbf{PP}^{\intercal})^{-1} = \begin{bmatrix} \mathbf{K}^{-1} \\ 0 \end{bmatrix} \\
& \mathbf{C} = \begin{bmatrix} 0 & 1 \end{bmatrix}^{\intercal} \\
& \mathbf{e}^{\prime} = \mathbf{P}^{\prime}\mathbf{C} = \mathbf{K}^{\prime}\mathbf{t}
\end{aligned}
\end{equation}
따라서 이에 대응하는 Fundamental Matrix $\mathbf{F}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{F} & = \mathbf{e}^{\prime\wedge}\mathbf{P}^{\prime}\mathbf{P}^{\dagger} \\
& = (\mathbf{K}^{\prime}\mathbf{t})^{\wedge}\mathbf{K}^{\prime}[\mathbf{R}|\mathbf{t}] \mathbf{K}^{-1}\begin{bmatrix} \mathbf{I} \\ 0 \end{bmatrix} \\
& = (\mathbf{K}^{\prime}\mathbf{t})^{\wedge}\mathbf{K}^{\prime}\mathbf{R}\mathbf{K}^{-1}
\end{aligned}
\end{equation}
1.5.5. Result 9.9
Canonical Form에 상응하는 Fundamental Matrix $\mathbf{F}$를 구해보면 두 카메라 행렬 $\mathbf{P} = [\mathbf{I}|0], \mathbf{P}^{\prime}=[\mathbf{M}|\mathbf{m}]$에 대해 다음 공식이 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{F} = \mathbf{m}^{\wedge}\mathbf{M}
\end{aligned}
\end{equation}
Canonical Form의 $\mathbf{F}$는 $\mathbf{F}=\mathbf{m}^{\wedge}\mathbf{M}$이다.
1.5.6. Projective ambiguity of cameras given F
1.5.7. Theorem 9.10
Fundamental Matrix $\mathbf{F}$는 Homography 변환에 상관없이 동일하기 때문에 필연적으로 모호성이 발생하게 된다. 만약 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$의 $\mathbf{F}$와 $(\tilde{\mathbf{P}}, \tilde{\mathbf{P}}^{\prime})$의 $\mathbf{F}$가 동일한 경우, $(\mathbf{P},\mathbf{P}^{\prime})$와 $(\tilde{\mathbf{P}}, \tilde{\mathbf{P}}^{\prime})$를 연결하는 Homography $\mathbf{H}$가 존재한다.
\begin{equation}
\begin{aligned}
& ^{\exists}\mathbf{H} \in \text{PGL}_{4} \\
& (\tilde{\mathbf{P}}, \tilde{\mathbf{P}}^{\prime}) = (\mathbf{P},\mathbf{P}^{\prime})\mathbf{H}
\end{aligned}
\end{equation}
1.5.8. Proof
두 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$, $(\tilde{\mathbf{P}}, \tilde{\mathbf{P}}^{\prime})$이 주어졌을 때 이를 Canonical Form으로 쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{P} = \tilde{\mathbf{P}} = [\mathbf{I}|0] \\
& \mathbf{P}^{\prime} = [\mathbf{A}|\mathbf{a}] \\
& \tilde{\mathbf{P}}^{\prime} = [\tilde{\mathbf{A}}|\tilde{\mathbf{a}}] \\
\end{aligned}
\end{equation}
이 때, Fundamental Matrix $\mathbf{F}$는
\begin{equation}
\begin{aligned}
\mathbf{F} = \mathbf{a}^{\wedge}\mathbf{A} = \tilde{\mathbf{a}}^{\wedge}\tilde{\mathbf{A}}
\end{aligned}
\end{equation}
가 성립한다. $\mathbf{F}$의 성질에 의해 $\mathbf{a}^{\intercal}\mathbf{F}=0, \tilde{\mathbf{a}}^{\intercal}\mathbf{F}=0$이 만족하게 되고
\begin{equation}
\begin{aligned}
& \mathbf{a}^{\intercal}\mathbf{F} = \mathbf{a}^{\intercal}\mathbf{a}^{\wedge}\mathbf{A} = 0 \\
& \tilde{\mathbf{a}}^{\intercal}\mathbf{F} = \tilde{\mathbf{a}}^{\intercal}\tilde{\mathbf{a}}^{\wedge}\tilde{\mathbf{A}} = 0 \\
\end{aligned}
\end{equation}
이 때, $\mathbf{a}$와 $\tilde{\mathbf{a}}$는 각각 rank 1인 $\mathbf{F}$의 Left Null Space가 된다. 따라서 $\mathbf{a}, \tilde{\mathbf{a}}$는
\begin{equation}
\begin{aligned}
\tilde{\mathbf{a}} = k \mathbf{a}, \ \ k \neq 0 \in \mathbb{R}
\end{aligned}
\end{equation}
인 관계가 성립한다. $\tilde{\mathbf{a}}$를 치환하여 다시 표현하면
\begin{equation}
\begin{aligned}
\mathbf{F} & = \mathbf{a}^{\wedge}\mathbf{A} = \tilde{\mathbf{a}}^{\wedge}\tilde{\mathbf{A}} = k\mathbf{a}^{\wedge}\tilde{\mathbf{A}} = 0 \\
& = \mathbf{a}^{\wedge}(k \tilde{\mathbf{A}} - \mathbf{A}) = 0
\end{aligned}
\end{equation}
따라서 $(k \tilde{\mathbf{A}} - \mathbf{A})$은 $\mathbf{a}$와 평행하다. 즉, 각 행렬의 열들이 배수 관계에 있다.
\begin{equation}
\begin{aligned}
k \tilde{\mathbf{A}} - \mathbf{A}= \mathbf{av}^{\intercal} \ \ \ \text{for some } \mathbf{v}
\end{aligned}
\end{equation}
따라서 $\tilde{\mathbf{A}} = k^{-1}(\mathbf{A}+\mathbf{av}^{\intercal})$가 된다. 카메라 행렬 대응쌍은 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{P} = \tilde{\mathbf{P}} = [\mathbf{I}|0] \\
& \mathbf{P}^{\prime} = [\mathbf{A}|\mathbf{a}] \\
& \tilde{\mathbf{P}}^{\prime} = [k^{-1}(\mathbf{A}+\mathbf{av}^{\intercal}) \ | \ k\mathbf{a}] \\
\end{aligned}
\end{equation}
결론적으로 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$를 Canonical Form으로 변환하는 행렬을 $\mathbf{H}_{1}$, $(\tilde{\mathbf{P}},\tilde{\mathbf{P}}^{\prime})$를 Canonical Form으로 변환하는 행렬을 $\mathbf{H}_{2}$라고 하면
\begin{equation}
\begin{aligned}
(\mathbf{P},\mathbf{P}^{\prime})\mathbf{H}_{1}\mathbf{H} = (\tilde{\mathbf{P}},\tilde{\mathbf{P}}^{\prime})\mathbf{H}_{2}
\end{aligned}
\end{equation}
를 만족하는 Homography $\mathbf{H}$가 존재하고 이에 따라 $(\mathbf{P},\mathbf{P}^{\prime})$과 $(\tilde{\mathbf{P}},\tilde{\mathbf{P}}^{\prime})$는 사영적으로 동등하다(projectively equivalent).
\begin{equation}
\begin{aligned}
(\mathbf{P},\mathbf{P}^{\prime}) \sim (\tilde{\mathbf{P}},\tilde{\mathbf{P}}^{\prime})
\end{aligned}
\end{equation}
1.6. Canonical cameras given F
1.6.1. Result 9.12
임의의 정방행렬 $\mathbf{F} \in \mathbb{R}^{3\times 3}$가 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$에 대응하는 Fundemental Matrix일 필요충분 조건은 $\mathbf{P}^{\prime\intercal}\mathbf{F}\mathbf{P}$가 반대칭 행렬(skew symmetric matrix)일 때이다.
\begin{equation}
\begin{aligned}
& \mathbf{x}^{\prime}\mathbf{Fx} = 0 \\
& \Leftrightarrow \mathbf{X}^{\intercal}\mathbf{P}^{\prime\intercal}\mathbf{FPX} =0 \ \ \forall \mathbf{X} \\
& \Leftrightarrow \mathbf{P}^{\prime\intercal}\mathbf{FP} \text{ is a skew symmetric matrix.}
\end{aligned}
\end{equation}
1.6.2. Result 9.13
임의의 정방행렬 $\mathbf{F} \in \mathbb{R}^{3\times 3}$가 주어지고 임의의 반대칭행렬 $\mathbf{S} \in \mathbb{R}^{3\times 3}$이 주어졌을 때 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$이 다음과 같다면
\begin{equation}
\begin{aligned}
& \mathbf{P} = [\mathbf{I} | 0 ] \\
& \mathbf{P}^{\prime} = [\mathbf{SF} | \mathbf{e}^{\prime}] \ \ \text{where, } \mathbf{e}^{\prime} \ \text{ is epipole.}
\end{aligned}
\end{equation}
이 때 $(\mathbf{P},\mathbf{P}^{\prime})$는 $\mathbf{F}$를 Fundamental Matrix로 갖는다.
이를 증명하기 위해 $\mathbf{P}^{\prime}\mathbf{FP}$를 전개해보면
\begin{equation}
\begin{aligned}
\mathbf{P}^{\prime}\mathbf{FP} & = [\mathbf{SF}|\mathbf{e}^{\prime}]^{\intercal} \mathbf{F} [\mathbf{I}|0] \\
& = \begin{bmatrix} \mathbf{F}^{\intercal}\mathbf{S}^{\intercal}\mathbf{F} & \mathbf{0} \\ \mathbf{e}^{\prime}\mathbf{F} & 0 \end{bmatrix} \\
& = \begin{bmatrix} \mathbf{F}^{\intercal}\mathbf{S}^{\intercal}\mathbf{F} & \mathbf{0} \\ \mathbf{0} & 0 \end{bmatrix} \\
\end{aligned}
\end{equation}
과 같이 반대칭행렬이므로 위 정리에 의해 $\mathbf{F}$가 Fundamental Matrix임을 알 수 있다.
반대칭행렬 $\mathbf{S}$는 3차원 벡터 $\mathbf{s}^{\wedge}$ 형태로 나타낼 수 있고 이 때, $\mathbf{s}^{\intercal}\mathbf{e}^{\prime} \neq 0$이면 $\mathbf{P}^{\prime} = [\mathbf{s}^{\wedge}\mathbf{F} | \mathbf{e}^{\prime}]$의 rank는 3이 된다. $\mathbf{P}^{\prime}$의 rank가 3이 되기 위해서는 $\mathbf{s}^{\wedge}\mathbf{F}, \mathbf{e}^{\prime}$의 rank는 각각 2,1이 되어야 한다. 우선, $\mathbf{s}^{\wedge}\mathbf{F}$가 rank 2라는 것을 증명해보면 Fundamental Matrix 성질에 의해 $\mathbf{e}^{\prime}\mathbf{F}=0$을 만족하므로 $\mathbf{F}$의 열공간 Col $\mathbf{F}$와 $\mathbf{e}^{\prime}$는 수직한다.
\begin{equation}
\begin{aligned}
\text{Col } \mathbf{F} \perp \mathbf{e}^{\prime}
\end{aligned}
\end{equation}
또한, $\mathbf{s}^{\wedge}\mathbf{e}^{\prime} \neq 0$이므로 $\mathbf{s}$는 Col $\mathbf{F}$ 안에 존재하지 않는다. $\mathbf{s}^{\wedge}\mathbf{F}$의 열공간은
\begin{equation}
\begin{aligned}
\text{Col } \mathbf{s}^{\wedge}\mathbf{F} & = \mathbf{s}^{\wedge} \text{Col } \mathbf{F} \\
& = \mathbf{s} \times \text{Col } \mathbf{F}
\end{aligned}
\end{equation}
이고 이 때 Col $\mathbf{F}$가 rank 2이므로 $\mathbf{s} \times \text{Col } \mathbf{F}$ 또한 rank 2 가 된다. 다음으로 $\mathbf{e}^{\prime}$가 다른 열벡터들과 선형독립임을 증명해보면 $\mathbf{s}^{\intercal} \text{Col } \mathbf{s}^{\wedge}\mathbf{F} = 0$이고 $\mathbf{s}^{\wedge}\mathbf{e}^{\prime} \neq 0$이므로
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime} \notin \text{Col } \mathbf{s}^{\wedge}\mathbf{F}
\end{aligned}
\end{equation}
결론적으로 $\mathbf{P}^{\prime} = [\mathbf{s}^{\wedge}\mathbf{F} | \mathbf{e}^{\prime}]$의 rank는 3이 된다.
1.6.3. Result 9.14
$\mathbf{P}^{\prime}$의 rank가 3이 되는 $\mathbf{s}$를 선택할 때 $\mathbf{e}^{\prime}$의 수직이 아닌 $\mathbf{s}$를 사용해야 하므로 $\mathbf{s}=\mathbf{e}^{\prime}$로 설정하면
\begin{equation}
\begin{aligned}
& \mathbf{P} = [\mathbf{I}|0] \\
& \mathbf{P}^{\prime} = [\mathbf{e}^{\prime\wedge}\mathbf{F} \ | \ \mathbf{e}^{\prime}]
\end{aligned}
\end{equation}
가 된다. 따라서, Fundamental Matrix $\mathbf{F}$가 주어졌을 때 $\mathbf{F}$의 Left Null Space $\mathbf{e}^{\prime}$를 계산함으로써 카메라 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$를 계산할 수 있다.
앞서 정의한 카메라 행렬 대응쌍의 비례식
\begin{equation}
\begin{aligned}
& (\mathbf{P}, \mathbf{P}^{\prime})= ([\mathbf{I}|0], [\mathbf{A}|\mathbf{a}]) \\
& (\tilde{\mathbf{P}},\tilde{\mathbf{P}}^{\prime}) = ([\mathbf{I}|0],[k^{-1}(\mathbf{A}+\mathbf{av}^{\intercal}) \ | \ k\mathbf{a}]) \\
\end{aligned}
\end{equation}
을 사용하여 일반적인 형태로 나타내면 다음과 같다.
1.6.4. Result 9.15
\begin{equation}
\begin{aligned}
& (\mathbf{P}, \mathbf{P}^{\prime})= ([\mathbf{I}|0], [\mathbf{e}^{\prime}\mathbf{F} \ | \ \mathbf{e}^{\prime}]) \\
& (\tilde{\mathbf{P}},\tilde{\mathbf{P}}^{\prime}) = ([\mathbf{I}|0],[\mathbf{e}^{\prime}\mathbf{F}+\mathbf{e}^{\prime}\mathbf{v}^{\intercal} \ | \ \lambda\mathbf{e}^{\prime}]) \\
\end{aligned}
\end{equation}
Null Space 값인 $\mathbf{e}^{\prime}$는 스케일에 불변하므로 $\frac{1}{k}\mathbf{e}^{\prime}$를 이용해도 결과는 동일하다. 따라서 위와 같은 형태로 나타낼 수 있다. 위 수식이 의미하는 바는 기존 $\mathbf{F}$에 임의의 벡터 $\mathbf{e}'\mathbf{v}^{\intercal}$와 임의의 스케일 값 $\lambda$를 곱해도 Fundamental Matrix에는 변화가 없다는 것을 의미한다. 이는 $\mathbf{F} = \mathbf{e}'^{\wedge}\mathbf{P}' \mathbf{P}^{\dagger} = \mathbf{e}'^{\wedge} \tilde{\mathbf{P}}' \tilde{\mathbf{P}}^{\dagger}$에 대입해보면 두 값에 관계없이 $\mathbf{F}$가 일정하게 나오기 때문이다. 즉, 위 식은 Fundamental Matrix의 사영모호성(Projective Ambiguity)을 내포하는 공식이 된다.
1.7. The essential matrix
Essential Matrix $\mathbf{E}$는 대응점 쌍 $\mathbf{x} \leftrightarrow \mathbf{x}'$가 정규 이미지 좌표계일 때 Fundamental Matrix를 의미한다. 역사적으로 Essential Matrix는 Longuet-Higgins에 의해 Fundamental Matrix보다 먼저 소개되었으며 이후 Essential Matrix의 일반화 버전으로 캘리브레이션되지 않은 대응점 쌍들에 대한 Fundamental Matrix가 소개되었다.
1.7.1. Normalized coordinates
임의의 카메라 행렬 $\mathbf{P} = \mathbf{K}[\mathbf{R}|\mathbf{t}]$가 주어졌을 때 이미지 평면 상의 점 $\mathbf{x}$에 대해 $\mathbf{x} = \mathbf{PX} = \mathbf{K}[\mathbf{R}|\mathbf{t}]\mathbf{X}$가 성립한다. 이 때, 정규화된 이미지 평면 위의 점을 $\bar{\mathbf{x}}$ 라고 하면
\begin{equation}
\begin{aligned}
\bar{\mathbf{x}} = \mathbf{K}^{-1}\mathbf{x}
\end{aligned}
\end{equation}
가 성립한다. 이 때,
\begin{equation}
\begin{aligned}
\mathbf{K}^{-1}\mathbf{P} = [\mathbf{R} | \mathbf{t}]
\end{aligned}
\end{equation}
를 정규카메라(normalized camera) 라고 한다. 정규카메라에서 카메라 행렬은 $\mathbf{K}= \mathbf{I}$인 경우로 생각할 수 있다. 정규카메라 행렬의 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$는
\begin{equation}
\begin{aligned}
(\mathbf{P},\mathbf{P}^{\prime}) = ([\mathbf{I}|0], \ [\mathbf{R}|\mathbf{t}])
\end{aligned}
\end{equation}
가 되므로 이 때 Fundamental Matrix $\mathbf{F} = \mathbf{t}^{\wedge}\mathbf{R}$이고 해당 행렬을 특별히 Essential Matrix $\mathbf{E}$ 라고 한다.
\begin{equation}
\begin{aligned}
\mathbf{E} = \mathbf{t}^{\wedge}\mathbf{R}
\end{aligned}
\end{equation}
1.7.2. Definition 9.16.
Essential Matrix은 $3\times 3$ 크기의 정방행렬이며 $\mathbf{E} \in \mathbb{R}^{3\times 3}$ 정규화된 이미지 좌표계에서 점들 간의 상관 관계 $\bar{\mathbf{x}} \leftrightarrow \bar{\mathbf{x}}^{\prime}$를 표현할 때 사용한다.
\begin{equation}
\begin{aligned}
\bar{\mathbf{x}}^{\prime\intercal}\mathbf{E}\bar{\mathbf{x}} = 0
\end{aligned}
\end{equation}
이 때, $\bar{\mathbf{x}} = \mathbf{K}^{-1}\mathbf{x}, \bar{\mathbf{x}}^{\prime} = \mathbf{K}^{-1}\mathbf{x}^{\prime}$이므로
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime\intercal}\mathbf{K}^{\prime-\intercal}\mathbf{E}\mathbf{K}^{-1}\mathbf{x} = 0
\end{aligned}
\end{equation}
이 성립하여 Fundamental Matrix $\mathbf{F}$와 Essential Matrix $\mathbf{E}$의 관계는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{F} & = \mathbf{K}^{\prime-\intercal}\mathbf{E}\mathbf{K}^{-1} \\
\mathbf{E} & = \mathbf{K}^{\prime\intercal}\mathbf{F}\mathbf{K}
\end{aligned}
\end{equation}
1.7.3. Properties of the essential matrix
- Essential Matrix $\mathbf{E} = \mathbf{t}^{\wedge}\mathbf{R}$는 5자유도(DOF)를 가진다. 회전 $\mathbf{R}$과 이동 $\mathbf{t}$ 각각 3개의 자유도를 갖지만 Fundamental Matrix와 동일하게 Homogeneous 성질에 의해 스케일 모호성(Scale Ambiguity)를 가지므로 1자유도를 잃는다. 줄어든 자유도는 Fundamental Matrix와 비교했을 때 Essential Matrix에 추가적인 제약조건을 형성한다.
- Essential Matrix를 특이값 분해(SVD) 했을 때 대각행렬 $\mathbf{D} = \begin{bmatrix} \sigma_{1} && \\ &\sigma_{2}& \\ &&\sigma_{3} \end{bmatrix}$ 의 가장 큰 두 특이값 $\sigma_{1}, \sigma_{2}$ 값은 서로 동일하고 세번째 특이값 $\sigma_{3}=0$을 만족한다. 자세한 내용은 다음 섹션에서 설명한다.
1.7.4. Result 9.17
임의의 정방행렬 $\mathbf{E} \in \mathbb{R}^{3\times 3}$이 Essential Matrix이기 위한 필요충분조건은 $\mathbf{E}$의 가장 큰 두 특이값 $\sigma_{1}, \sigma_{2}$ 값이 동일하고 세번째 특이값 $\sigma_{3}=0$인 조건이다.
1.7.5. Proof
Forward Proof: 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime}) = ([\mathbf{I}|0], \ [\mathbf{R}|\mathbf{t}])$에 대한 Fundamental Matrix $\mathbf{F}$가 있다고 하면
\begin{equation}
\begin{aligned}
\mathbf{F} = \mathbf{t}^{\wedge}\mathbf{R} = \mathbf{SR}
\end{aligned}
\end{equation}
이 된다. 반대칭행렬 $\mathbf{t}^{\wedge} = \mathbf{S}$가 rank 2를 가지는 경우 $\mathbf{S}$는 항상 기저(basis)를 변경하여 다음과 같은 형태로 변경할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{S} = k \mathbf{U}\mathbf{Z}\mathbf{U}^{\intercal}
\end{aligned}
\end{equation}
이 때, $k$는 임의의 스케일 값을 의미하고 일반적으로 고려하지 않는다. $\mathbf{U}$는 임의의 직교 행렬이며 $\mathbf{Z}$는 반대칭 행렬이다. $\mathbf{U}\mathbf{Z}\mathbf{U}^{\intercal}$를 SVD 형태에 맞게 변경하기 위해 약간의 대수적 트릭을 이용한다. 반대칭행렬 $\mathbf{Z}$와 직교행렬 $\mathbf{W}$를 아래와 같이 정의한다.
\begin{equation}
\begin{aligned}
\mathbf{Z} & = \begin{bmatrix} &1& \\ -1&& \\ && \end{bmatrix} \\
\mathbf{W} & = \begin{bmatrix} &-1& \\ 1&& \\ &&1 \end{bmatrix}
\end{aligned}
\end{equation}
두 행렬 사이에는 다음과 같은 유용한 성질이 존재한다. 해당 성질들은 본 섹션의 증명 과정에서 자주 등장하니 익혀두는 것을 권장한다.
\begin{equation}
\begin{aligned}
\mathbf{Z} & = \begin{bmatrix} 1&& \\ &1& \\ && \end{bmatrix}\mathbf{W} \quad \text{up to sign} \\
& =\text{diag}(1,1,0) \mathbf{W} \quad \text{up to sign} \\
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{ZW} & = -\mathbf{ZW}^{\intercal} \\
& = \begin{bmatrix} 1&& \\ &1& \\ && \end{bmatrix} \\
& = \text{diag}(1,1,0) \\
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{W}^{\intercal} & = \begin{bmatrix} -1&& \\ &-1& \\ &&1 \end{bmatrix}\mathbf{W} \\
\mathbf{W}\mathbf{W}^{\intercal} & = \mathbf{I}
\end{aligned}
\end{equation}
위 식에 따라 $\mathbf{U}\mathbf{Z}\mathbf{U}^{\intercal} = \mathbf{U}\text{diag}(1,1,0)\mathbf{W}\mathbf{U}^{\intercal}$과 같이 나타낼 수 있다. 이를 사용하여 Fundamental Matrix $\mathbf{F}$를 다시 나타내면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{F} & = \mathbf{SR} \\
& = \mathbf{UZU}^{\intercal}\mathbf{R} \\
& = \mathbf{U}\text{diag}(1,1,0)\mathbf{W}\mathbf{U}^{\intercal}\mathbf{R} \\
& \sim \mathbf{U} \text{diag}(1,1,0) \mathbf{V}^{\intercal} \quad \text{up to similarity}
\end{aligned}
\end{equation}
위 식에 따라 $\mathbf{F}$의 가장 큰 두 특이값은 같으며 마지막 특이값은 0이 된다. 이에 따라 Fundamental Matrix $\mathbf{F}$는 Essential Matrix $\mathbf{E}$의 성질을 만족하므로 Essential Matrix가 된다.
Reverse Proof: 반대로 임의의 정방행렬 $\mathbf{E} \in \mathbb{R}^{3\times 3}$의 특이값 분해(SVD)가
\begin{equation}
\begin{aligned}
\mathbf{E} \sim \mathbf{U} \begin{bmatrix} 1&& \\ &1& \\ &&0 \end{bmatrix}\mathbf{V}^{\intercal}
\end{aligned}
\end{equation}
을 만족하는 경우 이는
\begin{equation}
\begin{aligned}
\mathbf{E} & \sim \mathbf{U} \begin{bmatrix} 1&& \\ &1& \\ &&0 \end{bmatrix}\mathbf{V}^{\intercal} \\
& = \mathbf{U}\text{diag}(1,1,0)\mathbf{V}^{\intercal} \\
& = \mathbf{UZW}\mathbf{V}^{\intercal} \quad \quad \quad \because \mathbf{ZW} = \text{diag}(1,1,0) \\
& = \mathbf{UZU}^{\intercal}(\mathbf{UW}\mathbf{V}^{\intercal}) \quad \because \mathbf{U}^{\intercal}\mathbf{U}=\mathbf{I}\\
& = \mathbf{SR} \\
& = \mathbf{t}^{\wedge} \mathbf{R}
\end{aligned} \label{eq:1}
\end{equation}
이 된다. 네번째 행에서 3개의 직교행렬의 곱 $\mathbf{UW}\mathbf{V}^{\intercal}$은 회전행렬의 성질을 만족하므로 $\mathbf{R}$로 표시할 수 있다. 따라서 이 때 $\mathbf{E}$는 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime}) = ([\mathbf{I}|0], [\mathbf{R}|\mathbf{t}])$에 대응하는 Fundamental Matrix가 된다.
1.8. Extraction of cameras from the essential matrix
1.8.1. Result 9.18
Essential Matrix $\mathbf{E}$가 다음과 같이 주어졌을 때
\begin{equation}
\begin{aligned}
\mathbf{E} = \mathbf{U}\begin{bmatrix} 1&& \\ &1& \\ &&0 \end{bmatrix}\mathbf{V}^{\intercal}
\end{aligned}
\end{equation}
행렬 $\mathbf{E}$는 SR Factorization을 통해 $\mathbf{R}, \mathbf{t}$를 분해할 수 있다. 이 때, $\mathbf{R}$는 서로 부호가 다른 두 개의 SR Factorization 해를 가진다(up to sign).
\begin{equation}
\begin{aligned}
\mathbf{R} = \mathbf{U}\mathbf{W}\mathbf{V}^{\intercal} \quad \text{or} \quad \mathbf{U}\mathbf{W}^{\intercal}\mathbf{V}^{\intercal}
\end{aligned}
\end{equation}
1.8.2. Proof
(\ref{eq:1})에서 Essential Matrix $\mathbf{E}$는 다음과 같이 2개의 행렬로 분해가 가능하다.
\begin{equation}
\begin{aligned}
\mathbf{E} & = (\mathbf{UZU}^{\intercal})(\mathbf{UWV}^{\intercal}) = \mathbf{S}_{0}\mathbf{R}_{0}\\
& = (\mathbf{UZU}^{\intercal})(\mathbf{UW}^{\intercal}\mathbf{V}^{\intercal}) =\mathbf{S}_{0}\mathbf{R}_{0}^{\prime}\\
\end{aligned}
\end{equation}
위 식에서 두번째 행의 $(\mathbf{UW}^{\intercal}\mathbf{V}^{\intercal})$는 $-\mathbf{ZW}^{\intercal}$을 사용하여 $\text{diag}(1,1,0)$을 표현했을 때 얻는 행렬이다(up to sign). Essential Matrix $\mathbf{E}$가 위 두 가지 케이스로만 분해된다는 것을 증명하려면
\begin{equation}
\begin{aligned}
\mathbf{E} = \mathbf{S}_{0}\mathbf{R}_{0} = \mathbf{SR}
\end{aligned}
\end{equation}
에 대하여 $\mathbf{S} = \mathbf{S}_{0}, \mathbf{R} = \mathbf{R}_{0} = \mathbf{R}_{0}^{\prime}$임을 증명해야 한다.
반대칭행렬 $\mathbf{S}, \mathbf{S}_{0}$는 rank가 2인 행렬이므로 $\mathbf{S}_{0}^{\intercal} = \mathbf{s}_{0}^{\wedge}, \mathbf{S}^{\intercal} = \mathbf{s}^{\wedge}$과 같이 벡터 형태로 나타낼 수 있고
\begin{equation}
\begin{aligned}
\mathbf{s}, \mathbf{s}_{0} \in \text{Nul } \mathbf{E}^{\intercal}
\end{aligned}
\end{equation}
과 같이 $\mathbf{E}$의 Left Null Space에 포함된다. 따라서 $\mathbf{s}, \mathbf{s}_{0}$는 비례관계가 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{s} = \alpha \mathbf{s}_{0} \ \ \ \alpha \neq 0 \in \mathbb{R}
\end{aligned}
\end{equation}
위 식에 따라 $\mathbf{SR} = \alpha \mathbf{S}_{0}\mathbf{R}_{0}$이 성립하고 이 때, $\| \mathbf{R} \| = \| \mathbf{R}_{0} \| = 1$이므로 Frobenius Norm을 비교해보면 $\alpha = \pm 1$인 것을 알 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{S} = \pm \mathbf{S}_{0}
\end{aligned}
\end{equation}
다음으로 $\mathbf{R} = \mathbf{R}_{0} = \mathbf{R}_{0}^{\prime}$라는 것을 증명한다. 지금까지 구한 결과에 따라 Essential Matrix $\mathbf{E}$는 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{E} & = \mathbf{U} \begin{bmatrix} 1&& \\ &1& \\ &&0 \end{bmatrix} \mathbf{V}^{\intercal} \\
&= \mathbf{S}_{0}\mathbf{R} \\
& = \mathbf{S}_{0}(\mathbf{UXV}^{\intercal}) \quad \because \mathbf{R} = \mathbf{U}\mathbf{XV}^{\intercal} \\
& = \mathbf{U}\mathbf{ZU}^{\intercal}\mathbf{UXV}^{\intercal} \quad \because \mathbf{U}^{\intercal}\mathbf{U} = \mathbf{I} \\
& = \mathbf{U}(\mathbf{ZX})\mathbf{V}^{\intercal}
\end{aligned}
\end{equation}
이 때, 회전행렬 $\mathbf{R}$은 $\mathbf{R} = \mathbf{U}\mathbf{XV}^{\intercal}$와 같이 서로 다른 3개의 직교행렬로 분해가 가능하다.
$\mathbf{ZX} = \begin{bmatrix} &1& \\ -1&& \\ && \end{bmatrix}\mathbf{X} = \text{diag}(1,1,0)$이므로 이를 전개하면
\begin{equation}
\begin{aligned}
\mathbf{X} & = \begin{bmatrix} &-1& \\ 1&& \\ &&\pm1 \end{bmatrix} \\
& = \mathbf{W} = -\mathbf{W}^{\intercal}
\end{aligned}
\end{equation}
이므로 따라서 부호의 변화를 포함한(up to sign) $\mathbf{R} = \mathbf{R}_{0} = \mathbf{R}_{0}^{\prime}$가 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{R} = \mathbf{U}\mathbf{W}\mathbf{V}^{\intercal} \quad \text{or} \quad \mathbf{U}\mathbf{W}^{\intercal}\mathbf{V}^{\intercal}
\end{aligned}
\end{equation}
다음으로 $\mathbf{t}$를 구해보자. 반대칭행렬 $\mathbf{S} = \mathbf{U}\text{diag}(1,1,0)\mathbf{U}^{\intercal}= \mathbf{t}^{\wedge}$이므로 다음이 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{S}\mathbf{t} = \mathbf{t}^{\wedge}\mathbf{t} = 0
\end{aligned}
\end{equation}
위 식에서 $\mathbf{t}$의 해는 $\mathbf{S}$의 Null Space가 되므로 행렬 $\mathbf{U}$의 세 번째 열(third column)인 $\mathbf{u}_{3}$가 된다. 하지만 $\mathbf{S} = \pm\mathbf{S}_{0}$이므로
\begin{equation}
\begin{aligned}
\mathbf{t} = \pm \mathbf{u}_{3}
\end{aligned}
\end{equation}
이 되어 정확한 $\mathbf{t}$ 값을 결정할 수 없다.
1.8.3. Result 9.19
따라서 $\mathbf{t} = \pm \mathbf{u}_{3}$와 앞서 구한 $\mathbf{R} = \mathbf{U}\mathbf{W}\mathbf{V}^{\intercal}$ 또는 $\mathbf{R} = \mathbf{U}\mathbf{W}^{\intercal}\mathbf{V}^{\intercal}$에 의해 Essential Matrix $\mathbf{E} = \mathbf{t}^{\wedge}\mathbf{R}$에 대한 총 네 가지 경우의 수가 존재한다.
두 개의 카메라 행렬 $\mathbf{P}, \mathbf{P}'$와 Essential Matrix $\mathbf{E}$가 주어졌을 때, $\mathbf{P} = [\mathbf{I} \ | \ 0]$이라고 하면 $\mathbf{P}'$에 대한 다음과 같은 네 가지 해가 존재한다.
\begin{equation}
\begin{aligned}
\mathbf{P}' = [\mathbf{UWV}^{\intercal} | +\mathbf{u}_{3}] \text{ or } [\mathbf{UWV}^{\intercal} | -\mathbf{u}_{3}] \text{ or } [\mathbf{UW}^{\intercal}\mathbf{V}^{\intercal} | +\mathbf{u}_{3}] \text{ or } [\mathbf{UW}^{\intercal}\mathbf{V}^{\intercal} | -\mathbf{u}_{3}]
\end{aligned}
\end{equation}
1.9. Geometrical interpretation of the four solutions
위 네가지 해에서 처음 두 개의 솔루션을 보면 $\mathbf{u}_{3}$의 부호만 다른 것을 알 수 있는데 이는 첫 번째와 두 번째 카메라가 반대 방향으로 뒤집혀 있는 상태를 의미한다.
첫 번째 해와 세 번째 해는 다음과 같은 관계를 가진다.
\begin{equation}
\begin{aligned}
\mathbf{E} & = [\mathbf{UW}^{\intercal}\mathbf{V}^{\intercal} \ | \ \mathbf{u}_{3}] \quad \quad \quad \quad \quad \quad \cdots \text{3rd solution}\\
& = [\mathbf{U}(\mathbf{WV}^{\intercal}\mathbf{V}\mathbf{W}^{\intercal})\mathbf{W}^{\intercal}\mathbf{V}^{\intercal}\ | \ \mathbf{u}_{3}] \quad \because \mathbf{WV}^{\intercal}\mathbf{VW}^{\intercal} = \mathbf{I} \\
& = [\mathbf{UW}\mathbf{V}^{\intercal} \ | \ \mathbf{u}_{3}] \begin{bmatrix} \mathbf{VW}^{\intercal}\mathbf{W}^{\intercal}\mathbf{V}^{\intercal} & \\ & 1 \end{bmatrix} \\
& = [\mathbf{UW}\mathbf{V}^{\intercal} \ | \ \mathbf{u}_{3}] \begin{bmatrix} \mathbf{V}\begin{pmatrix} -1&& \\&-1& \\&&1 \end{pmatrix}\mathbf{V}^{\intercal} & \\ & 1 \end{bmatrix} \quad \cdots \text{1st solution} \cdot [*] \\
\end{aligned}
\end{equation}
이 때 $\mathbf{VW}^{\intercal}\mathbf{W}^{\intercal}\mathbf{V}^{\intercal}$는 Baseline의 수직한 방향 2개를 상하대칭하는 행렬이 된다. 즉, Baseline을 축으로 180 degree 회전하는 형태가 된다.

네 개의 해를 기하학적으로 표현하면 위 그림과 같다. 수학적으로는 총 네 개의 해가 도출되지만 실제 유효한 값은 하나만 존재한다. 따라서 3차원 공간 상의 점 $\mathbf{X}$가 두 카메라 앞에 존재하는 유일한 해를 선택하면 Essential Matrix $\mathbf{E}$를 분해한 $\mathbf{R}, \mathbf{t}$를 성공적으로 얻을 수 있다.
2. 3D Reconstruction of Cameras and Structure

이전 섹션에서 언급했듯이 Fundamental Matrix $\mathbf{F}$는 여러 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime})$에 대하여 사영모호성(projective ambiguity)이 존재하기 때문에 결과물인 $\mathbf{P}, \mathbf{P}^{\prime}$를 통해 계산한 3차원 공간 상의 점 또한 모호성을 가지게 된다. 해당 섹션에서는 Scene Constraint와 Internal Constraint를 사용하여 모호성을 제거하는 방법에 대해서 설명한다.
2.1. The projective reconstruction theorem
2.1.1. Theorem 10.1 (Projective reconstruction theorem)
두 카메라의 이미지 평면 상 대응쌍 점들인 $\mathbf{x}, \mathbf{x}^{\prime}$이 충분히 주어져서 이를 통해 Fundamental Matrix $\mathbf{F}$를 구했다고 가정해보자. 이 때, 사영모호성으로 인해 다음과 같은 두 카메라 행렬 대응쌍
\begin{equation}
\begin{aligned}
& (\mathbf{P}_{1}, \mathbf{P}_{1}^{\prime}, \{\mathbf{X}_{1,i}\}) \\
& (\mathbf{P}_{2}, \mathbf{P}_{2}^{\prime}, \{\mathbf{X}_{2,i}\}) \\
\end{aligned}
\end{equation}
이 동일한 Fundamental Matrix $\mathbf{F}$를 갖게 되는 경우
\begin{equation}
\begin{aligned}
& (\mathbf{P}_{2}, \mathbf{P}_{2}^{\prime}, \{\mathbf{X}_{2,i}\}) = \mathbf{H}\cdot (\mathbf{P}_{1}, \mathbf{P}_{1}^{\prime}, \{\mathbf{X}_{1,i}\}) \\
\end{aligned}
\end{equation}
를 만족하는 Homography 행렬 $\mathbf{H} \in \text{PGL}_{4}$가 반드시 존재한다. 이 때 $\cdot$ 연산은 다음과 같이 성립한다.
\begin{equation}
\begin{aligned}
& \mathbf{P}_{2} = \mathbf{H}\cdot\mathbf{P}_{1} = \mathbf{P}_{1}\mathbf{H}^{-1} \\
& \mathbf{P}_{2}^{\prime} = \mathbf{H}\cdot\mathbf{P}_{1}^{\prime} = \mathbf{P}_{1}^{\prime}\mathbf{H}^{-1} \\
&\mathbf{X}_{2i} = \mathbf{H}\cdot \mathbf{X}_{1i} = \mathbf{H}\mathbf{X}_{1i}
\end{aligned}
\end{equation}
2.1.2 Proof
이전 섹션에서 동일한 Fundamental Matrix $\mathbf{F}$를 공유하는 카메라 행렬 대응쌍 사이에 $\mathbf{P}_{2} = \mathbf{P}_{1}\mathbf{H}^{-1}, \mathbf{P}_{2}^{\prime} =\mathbf{P}_{1}^{\prime}\mathbf{H}^{-1}$를 만족하는 Homography 행렬 $\mathbf{H} \in \mathbb{R}^{4\times 4}$가 존재한다는 것을 증명하였다. 이를 적용해보면
\begin{equation}
\begin{aligned}
& \mathbf{P}_{2}\mathbf{X}_{2i} = \mathbf{P}_{1}\mathbf{H}^{-1}\mathbf{X}_{2i} = \mathbf{x}_{i} = \mathbf{P}_{1}\mathbf{X}_{1i} \\
& \mathbf{P}_{2}^{\prime}\mathbf{X}_{2i} = \mathbf{P}_{1}^{\prime}\mathbf{H}^{-1}\mathbf{X}_{2i} = \mathbf{x}_{i}^{\prime} = \mathbf{P}_{1}^{\prime}\mathbf{X}_{1i}
\end{aligned}
\end{equation}
가 성립한다. $\mathbf{P}_{1}, \mathbf{P}_{2}$에 의해 Back Projection된 직선을 $\mathcal{R}$이라고 하고 $\mathbf{P}_{1}^{\prime}, \mathbf{P}_{2}^{\prime}$에 의해 Back Projection된 직선을 $\mathcal{R}^{\prime}$이라고 하면
\begin{equation}
\begin{aligned}
\{\mathbf{H}^{-1}\mathbf{X}_{2i}, \mathbf{X}_{1i}\} \in \mathcal{R} \cap \mathcal{R}^{\prime}
\end{aligned}
\end{equation}
와 같이 3차원 공간 상의 점 $\{\mathbf{H}^{-1}\mathbf{X}_{2i}, \mathbf{X}_{1i}\}$는 두 직선의 교차점이 된다. 따라서 두 직선 $\mathcal{R}, \mathcal{R}^{\prime}$이 Baseline과 같이 동일한 직선인 경우를 제외하면 $\{\mathbf{H}^{-1}\mathbf{X}_{2i}, \mathbf{X}_{1i}\}$는 교차점인 한 점을 의미하므로
\begin{equation}
\begin{aligned}
& \mathbf{H}^{-1}\mathbf{X}_{2i} = \mathbf{X}_{1i} \\
& \mathbf{X}_{2i} = \mathbf{H}\mathbf{X}_{1i}
\end{aligned}
\end{equation}
가 성립한다. 따라서 추가적인 기하학적 원리를 사용하지 않으면 위와 같은 상황에서는 사영기하의 특성까지(up to projectivity) 복원할 수 있다.
2.2. Stratified reconstruction
Fundamental Matrix $\mathbf{F}$를 사용하여 계산한 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime})$의 사영모호성 문제를 해결하기 위해 Ground Truth 카메라 행렬 대응쌍인
\begin{equation}
\begin{aligned}
(\mathbf{P}_{0}, \mathbf{P}_{0}^{\prime}, \{\hat{\mathbf{X}_{i}}\})
\end{aligned}
\end{equation}
이 존재한다고 가정하면
\begin{equation}
\begin{aligned}
& (\mathbf{P}_{1}, \mathbf{P}_{1}^{\prime}, \{\mathbf{X}_{i}\}) = \mathbf{H}\cdot(\mathbf{P}_{0}, \mathbf{P}_{0}^{\prime}, \{\hat{\mathbf{X}_{i}}\}) \\
& \mathcal{T} = \mathbf{H}\cdot \mathcal{T}_{0}
\end{aligned}
\end{equation}
을 만족하는 Homography 행렬 $\mathbf{H}$가 존재한다. 이 때, 이미지 평면 상에서 평행한 직선의 특성을 활용하여 Affine Reconstruction을 수행한 다음, 이미지 평면 상에서 직교한 선들의 특성을 사용하여 Similarity Reconstruction을 순차적으로 수행한다.
2.2.1. The step to affine reconstruction

Affine Reconstruction 단계에서는 평행한 직선들의 특성을 보존하는 Homography 행렬 $\mathbf{H}_{A}$를 찾아야 한다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{A}(\pi_{\infty}) = \pi_{\infty}
\end{aligned}
\end{equation}
3차원 공간 상의 점들의 집합 $\{\mathbf{X}_{i}\}$를 사용하여 소실점을 3개 이상 구한 경우 이미지 평면에 투영된 무한대 평면 $\pi_{\infty}^{\prime}$를 계산할 수 있다. 이미지 평면 상에 투영된 무한대 평면 $\pi_{\infty}^{\prime}$를
\begin{equation}
\begin{aligned}
\pi_{\infty}^{\prime} = \begin{bmatrix} a & b & c & 1 \end{bmatrix}^{\intercal}
\end{aligned}
\end{equation}
라고 하면 실제 무한대 평면 $\pi_{\infty} = \begin{pmatrix} 0&0&0&1 \end{pmatrix}^{\intercal}$을 $\pi_{\infty}^{\prime}$로 보내는 Homography 행렬 $\mathbf{H}_{A}$는 다음과 같이 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{A} = \begin{bmatrix} \mathbf{I}_{3} \ | \ 0 \\ \pi^{\prime \intercal}_{\infty} \end{bmatrix}= \begin{bmatrix} &\mathbf{I}_{3}& & 0 \\ a&b&c&1 \end{bmatrix}
\end{aligned}
\end{equation}
이 때 $\mathbf{H}_{A}^{\intercal}\pi_{\infty} = \pi_{\infty}^{\prime}$ 관계가 성립한다.
\begin{equation}
\begin{aligned}
\pi_{\infty} = \mathbf{H}_{A}^{-\intercal} \pi_{\infty}^{\prime}
\end{aligned}
\end{equation}
이를 $\mathcal{T}$에 적용하면
\begin{equation}
\begin{aligned}
& \mathcal{T}_{a} = \mathbf{H} \cdot \mathcal{T} \\
& (\mathbf{PH}_{a}^{-1}, \mathbf{P}^{\prime}\mathbf{H}_{A}^{-1}, \{\mathbf{H}_{A}\mathbf{X}_{i}\}) = \mathbf{H} \cdot (\mathbf{P}, \mathbf{P}^{\prime}, \{\mathbf{X}_{i}\})
\end{aligned}
\end{equation}
연산을 통해 이미지를 Affine Reconstruction할 수 있다. 여기까지 진행했다면 Ground Truth $\mathcal{T}_{0}$와 $\mathcal{T}_{a}$는 Affine만큼만 차이가 나게 된다. 즉, 평행한 직선들은 모두 복원되었으나 아직 직교한 직선들은 복원되지 않은 상태이다.
2.2.2. The step to metric reconstruction
Metric Reconstruction 단계에서는 직교하는 선들을 보존하는 Homography 행렬 $\mathbf{H}_{S}$를 찾아야 한다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{S}(\Omega_{\infty}) = \Omega_{\infty}
\end{aligned}
\end{equation}
이 때, $\Omega_{\infty}$는 무한대 평면상에 존재하는 Absolute Conic을 의미한다. Affine Reconstruction 단계에서 얻은 $\mathcal{T}_{a}$는 무한대 평면 $\pi_{\infty}$가 실제 무한대에 위치하게 된다. 이 때, $\{\mathbf{X}_{i}\}$들 중 직교하는 점들을 사용하여 $\Omega_{\infty}$를 구할 수 있다. 직교하는 점들의 대응쌍을 $\mathbf{d}_{1}, \mathbf{d}_{2}$라고 하면
\begin{equation}
\begin{aligned}
\mathbf{d}_{1}^{\intercal}\omega \mathbf{d}_{2} = 0
\end{aligned}
\end{equation}
을 만족하는 $\omega$를 찾을 수 있고 $\omega$는 이미지 평면 상에 투영된 Absolute Conic $\Omega_{\infty}$ (Image of Absolute Conic, IAC)가 된다.
카메라 행렬 $\mathbf{P} = \mathbf{K} [\mathbf{R} | \mathbf{t}] = [\mathbf{M}\ | \ \mathbf{m}]$가 주어졌을 때 무한대 평면 $\pi_{\infty}$는 $\mathbf{M}$에 의해 이미지 평면 $\pi$에 투영된다.
\begin{equation}
\begin{aligned}
\mathbf{M}: \pi_{\infty} \mapsto \pi
\end{aligned}
\end{equation}
반대로 $\mathbf{M}^{-1}$는 $\pi$ 평면 상의 점들을 무한대 평면 $\pi_{\infty}$으로 보내는 매핑이라고 할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{M}^{-1}: \pi \mapsto \pi_{\infty}
\end{aligned}
\end{equation}
이 때, 이미지 평면에 투영된 Absolute Conic에 $\mathbf{M}^{-1}$을 적용하면 $\mathbf{M}^{-1}(\omega) = \tilde{\Omega}_{\infty}$가 된다. $\tilde{\Omega}_{\infty}$는 아직 Metric Reconstruction이 되기 전이므로 $\Omega_{\infty} \neq \tilde{\Omega}_{\infty}$이다. 둘 사이에는 다음 공식이 성립한다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{S}(\tilde{\Omega}_{\infty}) = \Omega_{\infty} = \mathbf{I}_{3}
\end{aligned}
\end{equation}
2.2.3. Result 10.5
이미지 평면에 프로젝션된 Absolute Conic을 $\omega$라고 하고 Affine Reconstruction으로 구한 카메라 행렬을 $\mathbf{P}=[\mathbf{M} \ | \ \mathbf{m}]$이라고 할 때 Metric Reconstruction을 수행하는 Homography $\mathbf{H}_{S}$는 다음과 같이 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{S} = \begin{bmatrix} \mathbf{A}^{-1} & \\ & 1 \end{bmatrix}
\end{aligned}
\end{equation}
이 때, $\mathbf{AA}^{\intercal} = (\mathbf{M}^{\intercal}\omega \mathbf{M})^{-1}$이고 $\mathbf{A}$는 이를 Cholesky Decomposition을 통해 얻을 수 있다.
2.2.4. Proof
Metric Reconstruction을 수행하는 Homography $\mathbf{H}_{S} = \begin{bmatrix} \mathbf{A}^{-1} & \\ & 1 \end{bmatrix}$이라고 하고 이 때 이미지 평면을 $\pi_{s}$, 카메라 행렬을 $\mathbf{P}_{s}$라고 하면 $\mathbf{H}_{S}(\pi) = \pi_{s}$ 관계가 성립하고 무한대 평면을 Homography 변환한 공식은
\begin{equation}
\begin{aligned}
& \pi_{\infty} \mathbf{A}^{-1} = \pi_{\infty,s} \\
& \mathbf{H}_{S}|_{\pi_{\infty}} = \mathbf{A}^{-1} \\
\end{aligned}
\end{equation}
가 된다. 각각 무한대 평면 $\pi_{\infty}, \pi_{\infty,s}$을 이미지 평면 $\pi, \pi_{s}$에 투영하는 공식은
\begin{equation}
\begin{aligned}
& \mathbf{P}|_{\pi_{\infty}} = \mathbf{M} \\
& \mathbf{P}_{s}|_{\pi_{\infty}} = \mathbf{MA}
\end{aligned}
\end{equation}
과 같이 변형된다. 따라서 $\mathbf{H}_{S}(\tilde{\Omega}_{\infty})$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{S}(\tilde{\Omega}_{\infty}) & = (\mathbf{A}^{-1})^{-\intercal} \tilde{\Omega}_{\infty} \mathbf{A} \\
& = \mathbf{A}^{\intercal} (\mathbf{M}^{\intercal}\omega \mathbf{M})\mathbf{A}
\end{aligned}
\end{equation}
따라서 Absolute Conic 특성에 의해 $\mathbf{A}^{\intercal} (\mathbf{M}^{\intercal}\omega \mathbf{M})\mathbf{A}$는 $\mathbf{I}$이 되어야 하므로
\begin{equation}
\begin{aligned}
& \mathbf{A}^{\intercal} (\mathbf{M}^{\intercal}\omega \mathbf{M})\mathbf{A} = \mathbf{I} \\
& (\mathbf{M}^{\intercal} \omega \mathbf{M})^{-1} = \mathbf{AA}^{\intercal}
\end{aligned}
\end{equation}
가 성립한다. 결론적으로 $\mathbf{H}_{S} = \begin{bmatrix} \mathbf{A}^{-1} & \\ & 1 \end{bmatrix}$를 구하기 위해서는 이미지 평면 상에서 직교하는 직선들의 특성을 사용하여 $\omega$를 구한 후, $(\mathbf{M}^{\intercal} \omega \mathbf{M})^{-1}$를 Cholesky Decomposition하여 $\mathbf{AA}^{\intercal}$를 구한다. 이를 통해 $\mathbf{A}^{-1}$ 값을 구할 수 있고 최종적으로 Metric Reconstruction을 수행하는 Homography $\mathbf{H}_{S}$를 구할 수 있다.
3. Computation of the Fundamental Matrix $\mathbf{F}$
3.1. Basic equations
두 카메라의 대응점쌍 $\mathbf{x} \leftrightarrow \mathbf{x}^{\prime}$이 존재할 때
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime\intercal}\mathbf{Fx} = 0
\end{aligned}
\end{equation}
을 만족하는 3x3 크기의 행렬 $\mathbf{F}$를 Fundamental Matrix라고 한다. 만약 세 개의 대응점쌍 $\mathbf{x} = (\mathbf{x}_{1}, \mathbf{x}_{2}, \mathbf{x}_{3})$, $\mathbf{x}^{\prime} = (\mathbf{x}_{1}^{\prime}, \mathbf{x}_{2}^{\prime}, \mathbf{x}_{3}^{\prime})$이 주어졌을 때 $\mathbf{x}^{\prime\intercal}\mathbf{Fx}=0$이를 다시 정리하면 $\sum \mathbf{x}^{\prime}_{i}\mathbf{x}_{j}\mathbf{f}_{ij}=0$과 같이 정리할 수 있다. 해당 식은 선형시스템
\begin{equation}
\begin{aligned}
\mathbf{A} \mathbf{f} = 0
\end{aligned}
\end{equation}
꼴로 나타낼 수 있고 이 때 $\mathbf{A}$와 $\mathbf{f}$를 풀어쓰면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{A} = (\mathbf{a}_{ik}) \in \mathbb{R}^{N \times 9}, \ \ \text{i-th row is} \ (\mathbf{x}_{1}^{\prime i}\mathbf{x}_{1}^{i}, \mathbf{x}_{1}^{\prime i}\mathbf{x}_{2}^{i},\cdots, \mathbf{x}_{n}^{\prime i}\mathbf{x}_{n}^{i}) \\
& \mathbf{f} = (\mathbf{f}_{11}, \mathbf{f}_{12}, \mathbf{f}_{13}, \cdots, \mathbf{f}_{33})^{\intercal} \in \mathbb{R}^{9\times 1} \\
& \mathbf{Af} = \begin{bmatrix} x'_{1}x_{1} & x'_{1}y_{1} & x'_{1} & y'_{1}x_{1} & y'_{1}y_{1} & y'_{1} & x_1 & y_1 & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x'_{n}x_{n} & x'_{n}y_{n} & x'_{n} & y'_{n}x_{n} & y'_{n}y_{n} & y'_{n} & x_n & y_n & 1 \end{bmatrix} \mathbf{f} = 0
\end{aligned}
\end{equation}
만약 주어진 대응점쌍의 개수 $N$이 8보다 크고 노이즈가 없는 완벽한 데이터로 생성이 되었으면 $\mathbf{A}$는 rank 8 행렬이 되고 유일한 해 $\mathbf{f}$가 존재한다. 이 때 $\mathbf{f}$는 $\mathbf{A}$의 Null Space의 원소가 된다.
하지만 대부분의 경우 주어진 데이터에는 항상 노이즈가 존재하므로 $\mathbf{A}$ 행렬은 rank 9인 full rank 행렬이 된다. 이 때 해를 구하면 $\mathbf{f}$는 항상 영벡터가 계산되므로 $\| \mathbf{f} \| = 1$이라는 조건하에 $\|\mathbf{Af}\|$의 크기를 최소화하는 근사해 $\mathbf{f}$를 찾아야 한다. 해를 찾는 방법은 $\mathbf{A}$를 특이값 분해(SVD)한 다음
\begin{equation}
\begin{aligned}
\mathbf{A} = \mathbf{UDV}^{\intercal}
\end{aligned}
\end{equation}
대각행렬 $\mathbf{D}$의 eigenvalue 중 가장 절대값이 작은 것에 대응되는 $\mathbf{V}$의 열벡터를 $\mathbf{f}$의 일반해로 간주한다. 해당 열벡터 $\mathbf{f}$가 $\|\mathbf{Af}\|$의 크기를 최소화하는 벡터가 되며 이를 Linear Solution이라고 부른다.
하지만 이 때, Linear Solution $\mathbf{f}$로 복원한 $\mathbf{F}_{0}$가 rank 2 행렬임을 보장할 수 없다. 수치적으로 해를 구하면 일반적으로 rank 3인 행렬이 나온다. 따라서 한 번 더 SVD를 사용하여 $\mathbf{F}_{0}$와 가장 가까운 rank 2 행렬을 찾아야 한다.
\begin{equation}
\begin{aligned}
\mathbf{F}_{0} = \mathbf{U}_{0}\mathbf{D}_{0}\mathbf{V}^{\intercal}_{0}
\end{aligned}
\end{equation}
이 때 대각행렬 $\mathbf{D}_{0} = \begin{bmatrix} \sigma_{1}&& \\ &\sigma_{2}& \\ &&\sigma_{3} \end{bmatrix}$는 일반적으로 마지막 특이값 $\sigma_{3}$가 0이 아니므로 rank 3인 행렬이 된다. 따라서 임의로 $\sigma_{3}=0$으로 변경한 행렬이 $\mathbf{F}_{0}$과 가장 가까운 rank 2 행렬이 된다.
3.1.1. The minimum case - seven point correspondences
7개의 대응점쌍이 주어진 경우 $\mathbf{A} \in \mathbb{R}^{7\times 9}$인 rank 7 행렬이 된다. 이에 따라 Null Space의 차원이 2가 되므로 무수한 해가 존재한다. $\mathbf{Af}=0$의 풀어서 두 개의 선형독립인 Fundamental Matrix $\mathbf{F}_{1}, \mathbf{F}_{2}$를 구하고
\begin{equation}
\begin{aligned}
\mathbf{F} = \alpha \mathbf{F}_{1} + (1-\alpha)\mathbf{F}_{2}
\end{aligned}
\end{equation}
를 통해 $\mathbf{F}$를 구한다. $\mathbf{F}$ 행렬의 rank는 2이므로 $\det(\mathbf{F})=0$을 만족하게 되고 이에 따라 $\alpha$에 대한 3차 방정식을 얻는다. 3차 방정식이 세 개의 실수해를 가지는 경우는 Degenerate Configuration이 된다.
3.2. The normalized 8-point algorithm
행렬 $\mathbf{A}$는 주어진 대응점쌍 $\mathbf{x} \leftrightarrow \mathbf{x}^{\prime}$으로 구성된 행렬이므로 대응점쌍들을 정규화(normalization)하지 않고 바로 해를 구하는 경우 $\mathbf{x}_{i} = (1000000,20000000,1)$과 같이 마지막 값에 비해서 처음 두 값의 크기가 매우 크게 되므로 수치적으로 불안정한 문제를 가진다. 따라서 $\mathbf{x}_{i}, \mathbf{x}_{i}^{\prime}$를 Centroid가 0이고 Centroid로부터 평균거리가 $\sqrt{2}$가 되도록하는 Homography 변환 $\mathbf{H}, \mathbf{H}^{\prime}$를 적용한다.
\begin{equation}
\begin{aligned}
& \mathbf{x}_{i} \rightarrow \mathbf{Hx}_{i} \\
& \mathbf{x}_{i}^{\prime} \rightarrow \mathbf{H}^{\prime} \mathbf{x}_{i}^{\prime} \\
\end{aligned}
\end{equation}
이렇게 변환된 대응쌍점들을 사용하여 수치적으로 안정적인 Fundamental Matrix $\mathbf{F}^{\prime}$ 계산할 수 있다. 앞서 설명한 내용을 따라 $\mathbf{F}^{\prime}$를 계산한 다음 다시 원래의 대응점쌍 $\mathbf{x} \leftrightarrow \mathbf{x}^{\prime}$으로 복원하기 위해
\begin{equation}
\begin{aligned}
0 & = (\mathbf{H}^{\prime}\mathbf{x}^{\prime})^{\intercal}\mathbf{F}^{\prime}(\mathbf{Hx}) \\
& = \mathbf{x}'^{\intercal}(\mathbf{H}^{\prime\intercal} \mathbf{F}^{\prime}\mathbf{H})\mathbf{x}
\end{aligned}
\end{equation}
처럼 $\mathbf{F} = \mathbf{H}^{\prime\intercal} \mathbf{F}^{\prime}\mathbf{H}$를 통해 원래 대응점쌍의 Fundamental Matrix $\mathbf{F}$를 계산할 수 있다.
3.2.1. Degenrate configurations
두 개의 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime}, \{\mathbf{X}_{i}\})$, $(\mathbf{Q}, \mathbf{Q}^{\prime}, \{\mathbf{Y}_{i}\})$가 다음의 조건을 만족하면 서로 Conjugate Configuration 이라고 한다.
\begin{equation}
\begin{aligned}
& \mathbf{PX}_{i} = \mathbf{QY}_{i}, \mathbf{P}^{\prime}\mathbf{x}_{i} = \mathbf{Q}^{\prime}\mathbf{Y}^{\prime} \ \ \forall s \\
& (\mathbf{P}, \mathbf{P}^{}), (\mathbf{Q}, \mathbf{Q}^{\prime}) \ \ \text{share the same} \ \ \mathbf{F}
\end{aligned}
\end{equation}
이 때, Conjuate Configuration이 있는 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime}, \{\mathbf{X}_{i}\})$을 Critical Triple이라고 부른다.
임의의 카메라 대응쌍 $\mathbf{P}, \mathbf{P}^{\prime}, \{\mathbf{X}_{i}\}$가 Critical Triple일 필요충분조건은 각각의 카메라 중심점 $\mathbf{C},\mathbf{C}^{\prime}$과 3차원 공간 상의 점 ${\mathbf{X}_{i}}$가 어떤 Ruled Quadric Surface, 즉 직선을 포함하는 Quadric Surface 상에 포함되는 것이다.
3.2.2. Proof
임의의 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime}, \{\mathbf{X}_{i}\})$이 Critical Triple이라는 것을 보이기 위해서는 이와 대응하는 카메라 행렬 대응쌍 $(\mathbf{Q}, \mathbf{Q}^{\prime}, \{\mathbf{Y}_{i}\})$이 같은 Fundamental Matrix $\mathbf{F}$를 가진다는 사실을 사용해야 한다. $\mathbb{P}^{3}$ 공간에서 이차곡면은 4x4 크기의 행렬로 정의된다.
\begin{equation}
\begin{aligned}
& \mathbf{S}_{p} := \mathbf{P}^{\prime}\mathbf{F}_{QQ^{\prime}}\mathbf{P}
\end{aligned}
\end{equation}
여기서 이차곡면 $\mathbf{S}_{p} \in \mathbb{R}^{4\times 4}$는 카메라 중심점 $\mathbf{C}, \mathbf{C}^{\prime}$과 3차원 공간 상의 점 $\{\mathbf{X}_{i}\}$를 포함해야 한다.
$\mathbf{S}_{p}$는 Ruled Quadric Surface이므로 직선을 포함하고 있음을 보이면 되므로 카메라 중심선을 연결한 직선인 baseline을 $\mathbf{S}_{p}$가 포함하고 있음을 보이면 된다. baseline 위에 있는 임의의 점 $\mathbf{X}$가 존재할 때
\begin{equation}
\begin{aligned}
\mathbf{S}_{p} \mathbf{X} = \mathbf{P}^{\prime}\mathbf{F}_{QQ^{\prime}}\mathbf{P}\mathbf{X} = 0 \quad \because \mathbf{F}_{QQ^{\prime}}\mathbf{PX} = 0
\end{aligned}
\end{equation}
을 만족하므로 $\mathbf{S}_{p}$는 Ruled Quadric Surface임을 알 수 있다.
반대로, 카메라 중심점 $\mathbf{C},\mathbf{C}^{\prime}$와 3차원 공간 상의 점 $\{\mathbf{X}_{i}\}$가 $\mathbf{S}_{p}$에 속하면 다음 공식이 성립한다.
\begin{equation}
\begin{aligned}
& (\mathbf{P}^{\prime}\mathbf{X}_{i})^{\intercal}\mathbf{F}_{QQ^{\prime}}(\mathbf{PX}_{i}) = 0 \\
\end{aligned}
\end{equation}
여기서 $\mathbf{x}^{\prime} = \mathbf{P}^{\prime}\mathbf{X}_{i}, \mathbf{x} = \mathbf{PX}_{i}$이고 $\mathbf{F}_{QQ^{\prime}}$이므로 $\mathbf{F}_{QQ^{\prime}}$에 대한 대응점 쌍이 $\mathbf{x}, \mathbf{x}^{\prime}$ 존재한다는 의미이다. 따라서
\begin{equation}
\begin{aligned}
& \mathbf{x}^{\prime} = \mathbf{P}^{\prime}\mathbf{X}_{i} = \mathbf{Q}^{\prime}\mathbf{Y}_{i} \\
& \mathbf{x} = \mathbf{P}\mathbf{X}_{i} = \mathbf{Q}\mathbf{Y}_{i} \\
\end{aligned}
\end{equation}
를 만족하므로 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime},\{\mathbf{X}_{i}\})$과 $(\mathbf{Q},\mathbf{Q}^{\prime},\{\mathbf{Y}_{i}\})$는 같은 Fundamental Matrix $\mathbf{F} = \mathbf{F}_{PP^{\prime}} = \mathbf{F}_{QQ^{\prime}}$를 공유하는 Conjugate Triple이라는 것을 알 수 있다.
3.3. The Gold Standard method
이미지 평면 상의 대응점 쌍 $\mathbf{x} \leftrightarrow \mathbf{x}^{\prime}$는 일반적으로 노이즈를 포함하고 있으므로 이를 통해 Fundamental Matrix $\mathbf{F}$를 정확하게 계산할 수 없고 $\|\mathbf{Af}\|$의 크기를 최소화하는 근사해 $\mathbf{F}^{\prime}$를 계산할 수 밖에 없다. 따라서 $\mathbf{F}^{\prime}$를 더 정확하게 계산하기 위해 2D Homography 문제와 마찬가지로 주어진 데이터 $\mathbf{x}, \mathbf{x}^{\prime}$를 Ground Truth $\hat{\mathbf{x}}, \hat{\mathbf{x}}^{\prime}$과 가까워지게 보정하는 방법을 The Gold Standard method 라고 한다.
- 8개 이상의 대응점 쌍 $\mathbf{x} \leftrightarrow \mathbf{x}^{\prime}$이 주어졌을 때 우선 앞서 설명한 것과 같이 총 두 번 SVD를 사용하여 rank가 2인 Fundamental Matrix $\mathbf{F}_{0}$를 계산한다. 이 때, $\mathbf{F}_{0}$를 Linear Solution이라고 부른다.
- 다음으로 Epipole $\mathbf{e}, \mathbf{e}^{\prime}$에 대하여 다음 공식이 성립한다.
\begin{equation}
\begin{aligned}
& \mathbf{e}^{\prime}\mathbf{F}_{0} = 0, \quad \mathbf{F}_{0}\mathbf{e} = 0 \\
\end{aligned}
\end{equation}
- 위 공식으로부터 $\mathbf{e}, \mathbf{e}^{\prime}$를 각각 계산한다.
- Epipole을 계산하면 Caninocal Form의 카메라 행렬 $\mathbf{P}, \mathbf{P}^{\prime}$를 계산할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{P} = [\mathbf{I}|0], \quad \mathbf{P}^{\prime} = [\mathbf{M}|\mathbf{m}] \\
& \text{where, } \ \mathbf{M} = \mathbf{e}^{\prime\wedge}\mathbf{F}, \ \mathbf{m} = \mathbf{e}^{\prime}
\end{aligned}
\end{equation}
- 이를 통해 $\mathbf{x}, \mathbf{x}^{\prime}$의 Back-projection된 직선들을 각각 구할 수 있다.
- 두 Back-projection 직선과 가장 근접한 3차원 공간 상의 점 $\mathbf{X}_{i}$를 계산할 수 있다.
- 이미지 평면에 3차원 공간 상의 점 $\mathbf{X}_{i}$를 재투영(reprojection) 한다.
\begin{equation}
\begin{aligned}
& \hat{\mathbf{x}} = \mathbf{PX}_{i} \\
& \hat{\mathbf{x}}^{\prime} = \mathbf{P}^{\prime}\mathbf{X}_{i} \\
\end{aligned}
\end{equation}
다음과 같이 재투영 오차(reprojection error)를 Gauss-Newton, Levenerg-Marquardt 등과 같은 비선형 최적화 방법을 사용하여 최소화한다.
\begin{equation}
\begin{aligned}
\sum_{i} d(\mathbf{x} - \hat{\mathbf{x}})^{2} + d(\mathbf{x}^{\prime}, \hat{\mathbf{x}}^{\prime})^{2}
\end{aligned}
\end{equation}
이 때 최적화되는 파라미터는 $\mathbf{X}_{i}$와 카메라 행렬 $\mathbf{P}^{\prime} = [\mathbf{M}|\mathbf{m}]$이다.
4. Structure Computation

4.1. Problem statement
해당 섹션에서는 두 카메라 행렬 대응쌍 $\mathbf{P},\mathbf{P}^{\prime}$와 이미지 평면의 대응점 쌍 $\mathbf{x}, \mathbf{x}^{\prime}$가 주어진 경우 $\mathbb{P}^{3}$ 공간 상의 점 $\mathbf{X}$를 구하는 방법에 대해 설명한다. 이론적으로는 대응점 쌍 $\mathbf{x}, \mathbf{x}^{\prime}$를 Back-projection하여 얻은 두 직선의 교차점을 통해 $\mathbf{X}$를 계산할 수 있으나 실제 데이터는 노이즈가 존재하기 때문에 두 Back-projection 직선이 교차하지 않는다. 또한 노이즈로 인해 두 이미지 평면 상에서 Epipolar Line $\mathbf{l}, \mathbf{l}^{\prime}$ 또한 $\mathbf{x}, \mathbf{x}^{\prime}$와 만나지 않는다.

이를 해결하기 위해서 두 Back-projection 직선들에 동시에 수직인 최단거리 직선을 구한 다음 최단거리 직선의 중점(mid-point)를 계산하여 $\mathbf{X}$를 계산하는 방법이 존재한다. 해당 방법은 체크보드를 이용한 캘리브레이션 방법과 같이 $\mathbf{P}, \mathbf{P}^{\prime}$가 고정된 경우에는 사용하면 좋은 방법이지만, 대부분의 경우 $\mathbf{P}, \mathbf{P}^{\prime}$는 사영모호성(projective ambiguity)으로 인해 유일하게 결정되지 않는다.
현실 세계에서는 카메라 행렬을 Affinity 또는 Projectivity까지 알고 있는 경우(up to affinity, projectivity)가 대부분이다. 정확한 $\mathbf{X}$를 구하기 위해서는 triangulation이 사영모호성에 대해서도 불변이어야 한다. Triangulation $\tau$은 주어진 대응점 쌍과 카메라 행렬 대응쌍으로부터 $\mathbf{X} \in \mathbb{P}^{3}$를 계산하는 방법을 말한다.
\begin{equation}
\begin{aligned}
\mathbf{X} = \tau(\mathbf{x},\mathbf{x}^{\prime},\mathbf{P},\mathbf{P}^{\prime})
\end{aligned}
\end{equation}
$\tau$가 사영모호성에 불변이기 위해서는 임의의 Homography $\mathbf{H}\in\text{PGL}_{4}$에 대하여
\begin{equation}
\begin{aligned}
\mathbf{X}_{H} & = \tau(\mathbf{x},\mathbf{x}^{\prime},\mathbf{PH}^{-1},\mathbf{P}^{\prime}\mathbf{H}^{-1}) \\
& = \mathbf{H}\cdot\tau(\mathbf{x},\mathbf{x}^{\prime},\mathbf{P},\mathbf{P}^{\prime}) \\
& = \mathbf{HX}
\end{aligned}
\end{equation}
공식이 성립해야 한다. 위와 같이 불변성이 성립하는 경우
\begin{equation}
\begin{aligned}
\mathbf{PH}^{-1} \mathbf{X}_{H} & = \mathbf{PH}^{-1}\mathbf{HX} \\
& = \mathbf{PX} \\
& = \mathbf{x}
\end{aligned}
\end{equation}
이 된다. 마찬가지로 $\mathbf{P}^{\prime}\mathbf{H}^{-1}\mathbf{X}_{H} = \mathbf{x}^{\prime}$이 된다. 예를 들어, Fundemantal Matrix $\mathbf{F}$와 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$, 대응점 쌍 $(\mathbf{x}, \mathbf{x}^{\prime})$이 주어졌을 때 $(\mathbf{P},\mathbf{P}^{\prime})$를 Homography 변환한 카메라 행렬 대응쌍 $(\mathbf{PH}^{-1},\mathbf{P}^{\prime}\mathbf{H}^{-1})$ 또한 동일한 $\mathbf{F}$를 공유한다. 이를 통해
\begin{equation}
\begin{aligned}
& \{\mathbf{X}\}: \ \text{ 3D Points from} \ (\mathbf{x},\mathbf{x}^{\prime}) \ \text{and } (\mathbf{P},\mathbf{P}^{\prime}). \\
& \{\mathbf{X}_{H}\}: \ \text{ 3D Points from} \ (\mathbf{x},\mathbf{x}^{\prime}) \ \text{and } (\mathbf{P}\mathbf{H}^{-1},\mathbf{P}^{\prime}\mathbf{H}^{-1}). \\
\end{aligned}
\end{equation}
과 같이 두 PointCloud $\{\mathbf{X}\},\{\mathbf{X}_{H}\}$를 구할 수 있고 PointCloud가 Homography에 불변이기 위해서는 두 PointCloud 사이에
\begin{equation}
\begin{aligned}
\mathbf{H}\{\mathbf{X}\} = \{\mathbf{X}_{H}\}
\end{aligned}
\end{equation}
인 변환 성질을 만족해야 한다. 앞서 설명한 중점(mid-point)을 사용한 방법은 두 Back-projection 직선들에 서로 수직인 최단거리 직선이 Homography 변환을 수행하면 더 이상 직교하지 않게 되고 중점 또한 더 이상 중심이 위치하지 않게 된다. 따라서 중점을 사용한 방법은 Homography에 불변하지 않다.
4.2. Linear triangulation methods
해당 섹션에서는 $\mathbf{X} \in \mathbb{P}^{3}$를 구하기 위해 선형방정식을 사용하는 방법을 설명한다. $\mathbf{x}=\mathbf{PX}, \mathbf{x}^{\prime}=\mathbf{P}^{\prime}\mathbf{X}$로부터
\begin{equation}
\begin{aligned}
& \mathbf{x}^{\wedge}(\mathbf{PX}) = 0\\
& \mathbf{x}^{\prime\wedge}(\mathbf{P}^{\prime}\mathbf{X})=0
\end{aligned}
\end{equation}
공식이 성립한다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = \begin{bmatrix} x&y&1 \end{bmatrix}^{\intercal} \\
& \mathbf{P} = \begin{bmatrix} \mathbf{p}_{1,row}^{\intercal} & \mathbf{p}_{2,row}^{\intercal} & \mathbf{p}_{3,row}^{\intercal} \end{bmatrix}^{\intercal} \\
& \mathbf{X} = \begin{bmatrix} X&Y&Z&W \end{bmatrix}^{\intercal}
\end{aligned}
\end{equation}
$\mathbf{p}_{i,row}^{\intercal}$를 $\mathbf{P}$의 i번째 행(row)라고 했을 때 $\mathbf{x}^{\wedge}(\mathbf{PX})$를 전개한 후 정리하면
\begin{equation}
\begin{aligned}
& x(\mathbf{p}_{3,row}^{\intercal}\mathbf{X}) - (\mathbf{p}_{1,row}^{\intercal}\mathbf{X}) = 0 \\
& y(\mathbf{p}_{3,row}^{\intercal}\mathbf{X}) - (\mathbf{p}_{2,row}^{\intercal}\mathbf{X}) = 0 \\
& x(\mathbf{p}_{2,row}^{\intercal}\mathbf{X}) - y(\mathbf{p}_{1,row}^{\intercal}\mathbf{X}) = 0 \\
\end{aligned}
\end{equation}
과 같고 이를 $\mathbf{x}^{\prime\wedge}(\mathbf{P}^{\prime}\mathbf{X})$도 같이 구한 후 $\mathbf{X}$에 대한 선형시스템으로 다시 작성하면
\begin{equation}
\begin{aligned}
& \underbrace{\begin{bmatrix}
x \mathbf{p}_{3,row}^{\intercal}-\mathbf{p}_{1,row}^{\intercal} \\
y \mathbf{p}_{3,row}^{\intercal}-\mathbf{p}_{2,row}^{\intercal} \\
x^{\prime} \mathbf{p}_{3,row}^{\prime\intercal}-\mathbf{p}_{1,row}^{\prime\intercal} \\
y^{\prime} \mathbf{p}_{3,row}^{\prime\intercal}-\mathbf{p}_{2,row}^{\prime\intercal} \\
\end{bmatrix}}_{\mathbf{A}}\mathbf{X} = 0 \\
\end{aligned}
\end{equation}
같이 $\mathbf{AX} = 0$ 형태로 정리할 수 있다. 데이터에 노이즈가 없는 경우 $\mathbf{A} \in \mathbb{R}^{4\times 4}$의 rank가 3이 되어 Null Space 벡터를 통해 유일한 $\mathbf{X}$를 계산할 수 있지만 노이즈가 존재하는 경우 $\mathbf{A}$의 rank는 4가 되어 무수히 많은 해가 존재한다. 따라서 $\mathbf{A}$를 특이값 분해(SVD)하여 $\|\mathbf{X} \|=1$일 때 $\|\mathbf{AX} \|$의 크기를 최소화하는 근사해 $\hat{\mathbf{X}}$를 계산해야 한다.
선형 방법에 Homography를 적용해보면
\begin{equation}
\begin{aligned}
y(\mathbf{p}_{3,row}^{}) - \mathbf{p}_{2,row}^{} & \rightarrow y(\mathbf{p}\mathbf{H}^{-1})_{3,row} - (\mathbf{p}\mathbf{H}^{-1})_{2,row} \\
& = y(\mathbf{p}_{3,row}^{})\mathbf{H}^{-1} - \mathbf{p}_{2,row}^{}\mathbf{H}^{-1} \\
& = (y(\mathbf{p}_{3,row}^{})-\mathbf{p}_{2,row}^{})\mathbf{H}^{-1}
\end{aligned}
\end{equation}
과 같이 $\mathbf{A} \Rightarrow \mathbf{AH}^{-1}$로 변환되어 $\mathbf{X} \Rightarrow \mathbf{X}_{H}$로 변환이 된다. 이를 통해
\begin{equation}
\begin{aligned}
\|\mathbf{AX}\| = \| \mathbf{AH}^{-1}\mathbf{X}_{H}\|
\end{aligned}
\end{equation}
이 성립하지만 Homography 변환을 할 때 $\|\mathbf{X}_{H} \| \neq 1$이 되어 $\|\mathbf{X}\|=1$의 성질을 보존하지 않는다. 따라서 선형방정식을 통한 방법은 Homography에 대해 불변이 아니므로 최적의 솔루션이 아니다.
4.2.1. Inhomogeneous method
카메라 행렬 대응쌍 $\mathbf{P},\mathbf{P}^{\prime}$이 Affine 변환까지(up to affinity) 결정되는 경우 $\mathbf{X}=(X,\ Y,\ Z,\ 1)^{\intercal}$로 놓고 $\|\mathbf{AX}\|$를 최소화하는 근사해 $\hat{\mathbf{X}}$를 구하는 방법을 Inhomogeneous method라고 한다. $\mathbf{X}$는 Affine Point이므로 $\|\mathbf{X}\|=1$ 제약조건이 사라지게 된다. 따라서, Inhomogeneous method는 임의의 Affine 변환 $\mathbf{H}_{A}$에 대해 불변인 특성을 지닌다.
4.3. An optimial solution
해당 섹션에서는 최적의 $\mathbf{X}\in\mathbb{P}^{3}$을 구하기 위한 Optimal Triangulation 방법에 대해 설명한다. 우선 비선형 최소제곱법(non-linear least square)을 통해 $\mathbf{X}$를 구하는 방법이 있다.
- 주어진 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$와 대응점 쌍 $(\mathbf{x},\mathbf{x}^{\prime})$에 대해여 이전 섹션에서 설명한 선형방정식 $\mathbf{AX}=0$을 통해 구한 근사해 $\hat{\mathbf{X}}$를 초기값 $\mathbf{X}_{0}$로 설정한다.
- $\mathbf{X}_{0}$를 각각 카메라에 프로젝션하면 $\hat{\mathbf{x}}, \hat{\mathbf{x}}^{\prime}$가 생성되는데 이 때 $d(\mathbf{x},\hat{\mathbf{x}})^{2}+d(\mathbf{x}^{\prime},\hat{\mathbf{x}}^{\prime})^{2}$를 최소화한다. $d(\mathbf{x}_{1},\mathbf{x}_{2})$은 $\mathbf{x}_{1}$과 $\mathbf{x}_{2}$ 사이의 거리를 의미한다.
- Gauss-Newton 또는 Levenberg-Marquardt와 같은 비선형 최소제곱법을 통해 반복적으로(iterative) 최적해 $\mathbf{X}^{\ast}$를 구한다.
4.3.1. Reformulation of the minimization problem

반복법을 사용하지 않고도(non-iterative) Optimal Triangulation을 수행할 수 있다. 해당 방법은 $d(\mathbf{x},\hat{\mathbf{x}})$를 최적화하는 대신 $\mathbf{x}$와 파라미터화된 Epipolar Line $\mathbf{l}(t)$ 사이의 거리 $d(\mathbf{x},\mathbf{l}(t))$를 최적화한다. 즉, $\mathbf{x}$와 $\mathbf{l}(t)$ 사이의 거리를 최소화하는 파라미터 $t$를 구함으로써 최적해를 구한다.
\begin{equation}
\begin{aligned}
\min_{t} d(\mathbf{x},\mathbf{l}(t))^{2} + d(\mathbf{x}^{\prime}, \mathbf{l}^{\prime}(t))^{2}
\end{aligned}
\end{equation}
4.3.2. Details of the minimization
우선 $\mathbf{x}=(x,y,1)^{\intercal}$와 $\mathbf{x}^{\prime}=(x^{\prime},y^{\prime},1)^{\intercal}$를 각각 원점 $(0,0,1)^{\intercal}$로 변환시킨다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = (x,y,1)^{\intercal} \rightarrow (0,0,1)^{\intercal} \\
& \mathbf{x}^{\prime} = (x^{\prime},y^{\prime},1)^{\intercal} \rightarrow (0,0,1)^{\intercal} \\
\end{aligned}
\end{equation}
이를 변환해주는 행렬을
\begin{equation}
\begin{aligned}
& \mathbf{T}=\begin{bmatrix} 1&&-x \\&1&-y \\ &&1\end{bmatrix} & \mathbf{T}^{\prime}=\begin{bmatrix} 1&&-x^{\prime} \\&1&-y^{\prime} \\ &&1\end{bmatrix}
\end{aligned}
\end{equation}
로 설정한다. 다음으로 Epipole $\mathbf{e}=(e_{1},e_{2},e_{3})^{\intercal}, \ \mathbf{e}^{\prime}=(e_{1}^{\prime},e_{2}^{\prime},e_{3}^{\prime})^{\intercal}$을 각각 x축 상의 점인 $(1,0,f)^{\intercal}, (1,0,f^{\prime})^{\intercal}$로 변환한다.
\begin{equation}
\begin{aligned}
& \mathbf{e}=(e_{1},e_{2},e_{3})^{\intercal} \rightarrow (1,0,f)^{\intercal} \\
& \mathbf{e}^{\prime}=(e_{1}^{\prime},e_{2}^{\prime},e_{3}^{\prime})^{\intercal} \rightarrow (1,0,f^{\prime})^{\intercal} \\
\end{aligned}
\end{equation}
이는 이미지 평면에서 각각 $(1/f,0)^{\intercal}, (1/f^{\prime},0)^{\intercal}$을 의미한다. 우선 $e_{1}^{2}+e_{2}^{2}=e_{1}^{\prime2}+e_{2}^{\prime2}=1$이 되도록 Epipole을 정규화한 다음, 이를 x축 상의 점으로 회전하는 행렬을 $\mathbf{R}, \mathbf{R}^{\prime}$ 다음과 같이 정의한다.
\begin{equation}
\begin{aligned}
& \mathbf{R} = \begin{bmatrix} e_{1}&e_{2}& \\ -e_{2}&e_{1}& \\ &&1 \end{bmatrix} & \mathbf{R}^{\prime} = \begin{bmatrix} e_{1}^{\prime}&e_{2}^{\prime}& \\ -e_{2}^{\prime}&e_{1}^{\prime}& \\ &&1 \end{bmatrix} &
\end{aligned}
\end{equation}
이를 통해 $\mathbf{Re}=(1,0,e_{3})^{\intercal}, \mathbf{R}^{\prime}\mathbf{e}^{\prime}=(1,0,e_{3}^{\prime})^{\intercal}$로 변환한다. 이 때, $e_{3}=f, e_{3}^{\prime}=f^{\prime}$이다. 다음으로 Epipolar Line $\mathbf{l}$을 $\mathbf{l}(t)$로 파라미터화한다. Epipole $\mathbf{e}=(1,0,f)^{\intercal}$는 x축 선상에 위치한 점이므로 이를 지나는 Epipolar Line은 y축을 기준으로 $(0,t,1)^{\intercal}$과 같이 파라미터화할 수 있다. 따라서 $\mathbf{l}(t)$는
\begin{equation}
\begin{aligned}
\mathbf{l}(t) & = \begin{pmatrix} 0\\t\\1 \end{pmatrix}\times \begin{pmatrix} 1\\0\\f \end{pmatrix} \\
& = \begin{pmatrix} tf\\1\\ -t \end{pmatrix}
\end{aligned}
\end{equation}
가 된다. 이전 단계에서 $\mathbf{x}$를 원점 $(0,0,1)^{\intercal}$로 옮겼으므로 $d(\mathbf{x},\mathbf{l}(t))$는
\begin{equation}
\begin{aligned}
d(\mathbf{x},\mathbf{l}(t))= \frac{t^{2}}{1^{2}+(tf)^{2}}
\end{aligned}
\end{equation}
이 된다. 다음으로 $\mathbf{l}^{\prime}(t)$를 계산해야 한다. Fundmamental Matrix $\mathbf{F}$를 사용하여 $\mathbf{l}^{\prime}(t)$를 계산하면
\begin{equation}
\begin{aligned}
& \mathbf{l}^{\prime}(t) = \mathbf{F}\begin{pmatrix} 0\\t\\1 \end{pmatrix}\\
& \because \mathbf{l}(t) \text{ is the epipolar line of } \begin{pmatrix} 0&t&1 \end{pmatrix}^{\intercal}.
\end{aligned}
\end{equation}
과 같다. $\mathbf{F}$는 주어진 카메라 행렬 대응쌍에서 $\mathbf{F}_{0}$를 계산한 후 $\mathbf{F}_{0}$로부터 $\mathbf{T},\mathbf{R},\mathbf{T}^{\prime},\mathbf{R}^{\prime}$을 이용하여 계산할 수 있다. Epipole과 $\mathbf{F}$ 사이에는
\begin{equation}
\begin{aligned}
& \mathbf{F}\begin{pmatrix} 1\\0\\f \end{pmatrix} = 0 \\
& \begin{pmatrix} 1&0&f^{\prime} \end{pmatrix}\mathbf{F}=0
\end{aligned}
\end{equation}
이 성립하므로 $\mathbf{F}_{1,col} = -f \mathbf{F}_{3,col}$ 그리고 $\mathbf{F}_{1,row} = -f^{\prime}\mathbf{F}_{3,row}$가 되고 이를 정리하면
\begin{equation}
\begin{aligned}
\mathbf{F} = \begin{bmatrix} f^{\prime}fd & -f^{\prime}c & -f^{\prime}d \\ -fb & a & b \\ -fd & c & d \end{bmatrix}
\end{aligned}
\end{equation}
가 된다. 이를 통해 $\mathbf{l}^{\prime}(t)$를 다시 표현하면
\begin{equation}
\begin{aligned}
\mathbf{l}^{\prime}(t) & = \mathbf{F}\begin{pmatrix} 0\\t\\1 \end{pmatrix} = t \mathbf{F}_{2,col} + \mathbf{F}_{3,col} \\
& = \begin{pmatrix} -f^{\prime}(ct+d) \\ at+b \\ ct+d \end{pmatrix}^{\intercal}
\end{aligned}
\end{equation}
이 된다. 다음으로 원점 $\mathbf{x}^{\prime}$와 $\mathbf{l}^{\prime}(t)$ 사이의 거리 $d(\mathbf{x}^{\prime}, \mathbf{l}^{\prime}(t))$를 구하면
\begin{equation}
\begin{aligned}
d(\mathbf{x}^{\prime}, \mathbf{l}^{\prime}(t))^{2} = \frac{(ct+d)^{2}}{(at+b)^{2} + f^{\prime2}(ct+d)^{2}}
\end{aligned}
\end{equation}
이 된다. 이를 통해 최적화하고자 하는 목적함수 $d(\mathbf{x},\mathbf{l}(t))^{2} + d(\mathbf{x}^{\prime}, \mathbf{l}^{\prime}(t))^{2}$는
\begin{equation}
\begin{aligned}
s(t) = \frac{t^{2}}{1+f^{2}t^{2}} + \frac{(ct+d)^{2}}{(at+b)^{2} + f^{\prime2}(ct+d)^{2}}
\end{aligned}
\end{equation}
가 되고 이를 미분하여 0$(s^{\prime}(t)=0)$이 되는 $t$를 찾으면 총 6개의 $t_{i}, \ i=1,\cdots,6$이 나오고 이 때 $s(t_{i})$ 값을 비교하여 최소가 되는 $t_{i}$를 찾는다. 이렇게 찾은 $t_{\min}$ 값을 사용한 $\mathbf{l}(t_{\min}), \mathbf{l}^{\prime}(t_{\min})$가 최적의 Epipolar Line이 된다. 다음으로
\begin{equation}
\begin{aligned}
& \hat{\mathbf{x}} = \mathbf{l}(t_{\min}) \\
& \hat{\mathbf{x}}^{\prime} = \mathbf{l}^{\prime}(t_{\min}) \\
& \hat{\mathbf{x}} \leftarrow \mathbf{T}^{-1}\mathbf{R}^{-1}\hat{\mathbf{x}} \\
& \hat{\mathbf{x}}^{\prime} \leftarrow \mathbf{T}^{\prime-1}\mathbf{R}^{\prime-1}\hat{\mathbf{x}}^{\prime} \\
\end{aligned}
\end{equation}
순서대로 변환하기 전 원래의 $\hat{\mathbf{x}}, \hat{\mathbf{x}}^{\prime}$을 복원한 다음
\begin{equation}
\begin{aligned}
& \hat{\mathbf{x}} \times \mathbf{P}\hat{\mathbf{X}} = 0 \\
& \hat{\mathbf{x}}^{\prime} \times \mathbf{P}\hat{\mathbf{X}}^{\prime} = 0 \\
\end{aligned}
\end{equation}
식을 $\mathbf{A}\hat{\mathbf{X}}=0$ 꼴로 정리하여 최종적으로 특이값 분해(SVD)를 통해 최적해 $\hat{\mathbf{X}}$를 구한다. 이와 같이 $\mathbf{X}$의 근사해를 구하는 방법을 Optimal Triangulation 방법이라고 한다.
5. Scene planes and homographies
5.1. Homographies given the plane and vice versa

해당 섹션에서는 월드 상의 평면 $\pi$이 주어졌을 때 이를 사용하여 하나의 이미지 평면에서 다른 이미지 평면으로 가는 Homography 변환에 대해 설명한다.
5.1.1. Result 13.1
Canonical Form으로 변환한 카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime})$과 월드 상의 평면 $\pi$ 다음과 같이 주어졌을 때
\begin{equation}
\begin{aligned}
& \mathbf{P} = [\mathbf{I} \ | \ 0] \\
& \mathbf{P}^{\prime} = [\mathbf{A} \ | \ \mathbf{a}] \\
& \pi = (\mathbf{v}^{\intercal}, 1)^{\intercal} \quad \mathbf{v} \in \mathbb{R}^{3}
\end{aligned}
\end{equation}
이 때, Homography $\mathbf{H}$는
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{A} - \mathbf{av}^{\intercal}
\end{aligned}
\end{equation}
로 주어진다.
5.1.2. Proof
두 카메라의 이미지 평면 $\pi_{\mathbf{P}}, \pi_{\mathbf{P}^{\prime}}$가 주어졌을 때, 월드 평면 상의 점 $\mathbf{X} \in \pi$를 $\pi_{\mathbf{P}}$ 평면으로 프로젝션한 점 $\mathbf{x}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{PX} & = [\mathbf{I}\ | \ 0]\begin{bmatrix} \tilde{\mathbf{X}} \\ 1 \end{bmatrix} \\
& = \tilde{\mathbf{X}} = \mathbf{x}
\end{aligned}
\end{equation}
따라서 임의의 스칼라 $\rho$에 대해 $\tilde{\mathbf{X}} = \rho^{-1}\mathbf{x}$가 성립한다. $\mathbf{X}$를 다시 쓰면 $\mathbf{X}=\begin{bmatrix} x & \rho \end{bmatrix}^{\intercal}$이 되고 $\mathbf{X}$는 $\pi$ 평면 위의 점이므로
\begin{equation}
\begin{aligned}
\begin{bmatrix} \mathbf{v}^{\intercal} & 1 \end{bmatrix} \begin{bmatrix} \mathbf{x} \\ \rho \end{bmatrix} = 0
\end{aligned}
\end{equation}
이 성립한다. 위 식을 풀면 $\rho = -\mathbf{v}^{\intercal}\mathbf{x}$이 된다. $\mathbf{X}$를 $\pi_{\mathbf{P}^{\prime}}$에 프로젝션하면
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime} & = \mathbf{P}^{\prime}\mathbf{X} = [\mathbf{A} \ | \ \mathbf{a}]\begin{bmatrix} \mathbf{x} \\ -\mathbf{v}^{\intercal}\mathbf{x} \end{bmatrix} \\
& = \mathbf{Ax} - \mathbf{av}^{\intercal}\mathbf{x} \\
& = (\mathbf{A}-\mathbf{av}^{\intercal})\mathbf{x}
\end{aligned}
\end{equation}
이 되므로 따라서 $\mathbf{H} = \mathbf{A}-\mathbf{av}^{\intercal}$이 된다.
5.1.3. A calibrated stereo rig
캘리브레이션 된 스테레오 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$가 다음과 같이 주어지고
\begin{equation}
\begin{aligned}
& \mathbf{P} = \mathbf{K}[\mathbf{I} \ | \ 0] \\
& \mathbf{P}^{\prime} = \mathbf{K}^{\prime}[\mathbf{R} \ | \ \mathbf{t}]
\end{aligned}
\end{equation}
월드 상의 평면 $\pi=(\mathbf{n}^{\intercal},d)^{\intercal}$이 주어진 경우, $\pi$ 평면 상의 점 $\mathbf{X}$는
\begin{equation}
\begin{aligned}
\mathbf{n}^{\intercal}\tilde{\mathbf{X}}+d=0
\end{aligned}
\end{equation}
이 성립한다. 이를 다시 정리하면 $-\frac{\mathbf{n}^{\intercal}\tilde{\mathbf{X}}}{d}=1$이 된다. $\mathbf{X}$를 이미지 평면 $\pi_{\mathbf{P}}$ 상에 프로젝션한 점 $\mathbf{x}$는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{x} & = \mathbf{P}\mathbf{X} = \mathbf{K}[\mathbf{I}\ | \ 0]\begin{bmatrix} \tilde{\mathbf{X}} \\ 1\end{bmatrix} \\
& = \mathbf{K}\tilde{\mathbf{X}}
\end{aligned}
\end{equation}
따라서 $\tilde{\mathbf{X}} = \mathbf{K}^{-1}\mathbf{x}$가 되고 다음으로 $\mathbf{X}$를 이미지 평면 $\pi_{\mathbf{P}^{\prime}}$에 프로젝션한 점 $\mathbf{x}^{\prime}$는
\begin{equation}
\begin{aligned}
\mathbf{x}^{\prime} & = \mathbf{P}^{\prime}\mathbf{X} = \mathbf{K}^{\prime}[\mathbf{R}\ | \ \mathbf{t}]\begin{bmatrix} \tilde{\mathbf{X}} \\ 1\end{bmatrix} \\
& = \mathbf{K}^{\prime}\mathbf{R}\tilde{\mathbf{X}} + \mathbf{K}^{\prime}\mathbf{t}(-\frac{\mathbf{n^{\intercal}\tilde{\mathbf{X}}}}{d}) \\
& = \mathbf{K}^{\prime}(\mathbf{R}-\frac{\mathbf{tn}^{\intercal}}{d})\tilde{\mathbf{X}} \\
& = \mathbf{K}^{\prime}(\mathbf{R}-\frac{\mathbf{tn}^{\intercal}}{d})\mathbf{K}^{-1}\mathbf{x} \\
\end{aligned}
\end{equation}
가 되어 결론적으로 캘리브레이션된 스테레오 카메라에서 Homography $\mathbf{H}$는
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{K}^{\prime}(\mathbf{R}-\frac{\mathbf{tn}^{\intercal}}{d})\mathbf{K}^{-1} \\
\end{aligned}
\end{equation}
가 된다.
5.1.4. Homographies compatible with epipolar geometry

월드 상의 평면 $\pi$ 위에 존재하는 4개의 대응점 쌍 $(\mathbf{x}_{i}, \mathbf{x}_{i}^{\prime}), \ i=1,\cdots,4$가 주어졌다고 가정해보자. 4개의 대응점 쌍으로부터 8개의 제약조건을 얻을 수 있으며 이를 통해 Homograpy $\mathbf{H}$를 유일하게 결정할 수 있다.
다음으로 월드 상에 서로 일직선으로 있지 않은(no three are collinear) 임의의 4개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), i=1,\cdots,4$가 주어졌다고 가정해보자. 이 때, 한 이미지 평면 $\pi_{\mathbf{P}}$에서 다른 이미지 평면 $\pi_{\mathbf{P}^{\prime}}$으로 점들을 변환하는 Homography $\mathbf{H}$가 존재하게 되는데 이러한 $\mathbf{H}$가 두 카메라 사이의 Fundamental Matrix $\mathbf{F}$와 서로 호환(compatible)이 되기 위해서는 $\mathbf{H}$가 월드 평면 상의 평면 $\pi$에 대한 Homography 변환이어야 한다. 다시 말하면, $\mathbf{H}$가 Epipolar Geometry를 따르기 위해서는 $\mathbf{H}$가 $\pi$에 대한 Homography이어야 한다. Epipolar Geometry에 의해 $\mathbf{x}$가 $\mathbf{Hx}$와 대응이 되기 위한 조건은
\begin{equation}
\begin{aligned}
(\mathbf{Hx})^{\intercal}\mathbf{F}\mathbf{x} = 0
\end{aligned}
\end{equation}
이다. 즉, $\mathbf{x}^{\intercal}\mathbf{H}^{\intercal}\mathbf{Fx}=0$을 만족해야 하므로 $\mathbf{H}^{\intercal}\mathbf{F}$가 반대칭행렬(skew-symmetric)이어야 한다.
\begin{equation}
\begin{aligned}
\mathbf{H}^{\intercal}\mathbf{F} + \mathbf{F}^{\intercal}\mathbf{H} = 0
\end{aligned}
\end{equation}
위 조건은 $\mathbf{H}$가 Epipolar Geometry를 따르기 위한 필요충분조건이다.
5.1.5. Result 13.3
일반적으로 $\mathbf{F}=\mathbf{e}^{\prime\wedge}\mathbf{A}$와 같이 주어졌을 때 $\mathbf{H}$는
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{A} - \mathbf{e}^{\prime}\mathbf{v}^{\intercal}
\end{aligned}
\end{equation}
이 된다. 이 때, $\mathbf{H}$는 $\mathbf{v} \in \mathbb{R}^{3}$로부터 3자유도를 가진다.
5.1.6. Proof
$\mathbf{F}=\mathbf{e}^{\prime\wedge}\mathbf{A}$와 같이 주어진 경우 Projective Reconstruction을 수행하면 두 카메라 행렬 대응쌍을
\begin{equation}
\begin{aligned}
& \mathbf{P} = [\mathbf{I} \ | \ 0] \\
& \mathbf{P}^{\prime} = [\mathbf{A} \ | \ \mathbf{e}^{\prime}]
\end{aligned}
\end{equation}
과 같이 구할 수 있다. 월드 상의 평면 $\pi=(\mathbf{v}^{\intercal}, 1)^{\intercal}$이 주어졌을 때 앞의 정리에 의해
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{A} - \mathbf{e}^{\prime}\mathbf{v}
\end{aligned}
\end{equation}
와 같이 구할 수 있다. 이를 $\mathbf{F}^{\intercal}\mathbf{H}$에 대입하면
\begin{equation}
\begin{aligned}
\mathbf{F}^{\intercal}\mathbf{H} & = -\mathbf{A}^{\intercal}\mathbf{e}^{\prime\wedge}(\mathbf{A}-\mathbf{e}^{\prime\intercal}\mathbf{v}) \\
& = -\mathbf{A}^{\intercal}\mathbf{e}^{\prime\wedge}\mathbf{A} \quad \because \mathbf{e}^{\prime\wedge}\mathbf{e}^{\prime} = 0
\end{aligned}
\end{equation}
와 같이 반대칭행렬(skew-symmetric)이 된다.
5.1.7. Corollary
두 카메라 사이의 임의의 Homography $\mathbf{H}$가 Epipolar Geometry를 따르기 위해서는 $\mathbf{H}$가 월드 상의 평면 $\pi$에 대한 Homography이어야 한다. $\mathbf{H}$가 월드 상의 평면 $\pi$에 대한 Homography이기 위한 필요충분조건은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{F} = \mathbf{e}^{\prime\wedge}\mathbf{H}
\end{aligned}
\end{equation}
5.1.8. Proof
($\Rightarrow$) $\mathbf{H}$가 월드 상의 평면 $\pi=(\mathbf{v}^{\intercal},1)^{\intercal}$에 대한 Homography이면서 $\mathbf{F}=\mathbf{e}^{\prime\wedge}\mathbf{A}$일 때 앞서 정리에 의해
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{H}_{\begin{pmatrix} \mathbf{v}\\1 \end{pmatrix}} = \mathbf{A} - \mathbf{e}^{\prime\intercal}\mathbf{v}
\end{aligned}
\end{equation}
가 성립한다. 따라서
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime\wedge}\mathbf{H} & = \mathbf{e}^{\prime\wedge}(\mathbf{A}-\mathbf{e}^{\prime\intercal}\mathbf{v}) \\
& = \mathbf{e}^{\prime\wedge}\mathbf{A} = \mathbf{F} \quad \because \mathbf{e}^{\prime\wedge}\mathbf{e}^{\prime} = 0
\end{aligned}
\end{equation}
가 된다.
($\Leftarrow$) $\mathbf{F}=\mathbf{e}^{\prime\wedge}\mathbf{H}$인 경우 $\mathbf{H}$는 월드 상의 임의의 평면 $\pi$에 의한 Homography이다. 예를 들어, $\mathbf{H}$가 무한대 평면 $\pi_{\infty}=(\mathbf{0}^{\intercal},1)^{\intercal}$에 의한 Homography라고 하면
\begin{equation}
\begin{aligned}
\mathbf{H} & = \mathbf{H}_{\begin{pmatrix} \mathbf{0}\\1 \end{pmatrix}} = \mathbf{H} - \mathbf{e}^{\prime}\cdot 0 = \mathbf{H}
\end{aligned}
\end{equation}
가 된다.
5.2. Plane induced homographies given $\mathbf{F}$ and image correspondences
5.2.1. Three points

두 개의 이미지 평면 $\pi_{\mathbf{P}}, \pi_{\mathbf{P}^{\prime}}$에 세 개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), \ i=1,2,3$이 주어졌을 때 이들을 Back-projection한 월드 상의 점 $\mathbf{X}_{i}, \ i=1,2,3$을 통해 월드 상의 평면 $\pi$를 유일하게 결정할 수 있고 이를 통한 Homography $\mathbf{H}$를 계산할 수 있다. 해당 섹션에서는 이러한 Homography $\mathbf{H}$를 구하는 방법에 대해 설명한다.
$\mathbf{H}$를 구하는 방법에는 크게 두 가지 방법이 존재한다. 첫 번째 방법은 월드 상의 평면 $\pi$를 직접 구하는 방법이 있다. 세 개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), \ i=1,2,3$과 Fundamental Matrix $\mathbf{F}=\mathbf{e}^{\prime\wedge}\mathbf{A}$가 주어진 경우 이를 통해 카메라 행렬을 구할 수 있다(projective reconstrcution). 주어진 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), \ i=1,2,3$과 $\mathbf{F}$를 통해
\begin{equation}
\begin{aligned}
& \mathbf{P} = [\mathbf{I}\ | \ 0] \\
& \mathbf{P}^{\prime} = [\mathbf{A} \ | \ \mathbf{e}^{\prime}]
\end{aligned}
\end{equation}
을 사영모호성을 포함하여(up to projectivity) 결정할 수 있다. 그리고 $\mathbf{P},\mathbf{P}^{\prime}$를 사용하여 Back-projection한 월드 상의 점 $\mathbf{X}_{i},\ i=1,2,3$ 또한 계산할 수 있다. 이 때, $\mathbf{X}_{i},\ i=1,2,3$은 동일한 직선 상에 존재하면 안된다(not colinear). 다음으로 월드 상의 세 개의 점 $\mathbf{X}_{i},\ i=1,2,3$을 포함하는 월드 상의 평면 $\pi$를 유일하게 결정할 수 있고 $\pi=(\mathbf{v}^{\intercal},d)^{\intercal}$일 때
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{A} - \mathbf{e}^{\prime}\mathbf{v}^{\intercal}
\end{aligned}
\end{equation}
과 같이 $\pi$를 기반으로 $\pi_{\mathbf{P}} \leftrightarrow \pi_{\mathbf{P}^{\prime}}$ 사이의 점들을 변환하는 Homography $\mathbf{H}$를 계산할 수 있다.
두 번째 방법은 $\mathbf{Hx}_{i} = \mathbf{x}^{\prime}_{i},\ i=1,2,3$을 대수적으로 푸는 방법이다. 이 때 $\mathbf{x}^{\prime}_{i} \times (\mathbf{Hx}_{i}) = 0$의 공식을 선형방정식의 $\mathbf{Ah}=0$ 형태로 변형함으로써 Homography $\mathbf{H}$를 구할 수 있다. 하지만 Homography $\mathbf{H}$를 구하려면 총 네 개의 대응점 쌍이 필요한데 주어진 대응점 쌍은 세 개이므로 추가적으로 한 개의 대응점 쌍이 필요하다. 미리 알고 있는 Fundamental Matrix $\mathbf{F}$를 사용하여 두 이미지 평면의 Epipole $\mathbf{e},\mathbf{e}^{\prime}$을 구하고 이를 Back-projection함으로써 한 개의 대응점쌍을 추가하여 Homography $\mathbf{H}$를 계산할 수 있다. 단, 이 때 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), i=1,2,3$들이 Epipolar Line 위에 존재하면 안된다는 가정이 필요하다.
5.2.2. Result 13.6
Fundamental Matrix $\mathbf{F}$와 세 개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), i=1,2,3$이 주어졌을 때 이들을 통해 계산한 월드 상의 평면 $\pi$로 인한 Homography $\mathbf{H}$는
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{A} - \mathbf{e}^{\prime}(\mathbf{M}^{-1}\mathbf{b})^{\intercal}
\end{aligned}
\end{equation}
와 같이 계산할 수 있다. 이 때,
\begin{equation}
\begin{aligned}
& \mathbf{M} = \begin{bmatrix} \mathbf{x}_{1}\\\mathbf{x}_{2} \\ \mathbf{x}_{3} \end{bmatrix} \\
& \mathbf{b} = (\mathbf{x}^{\prime}_{i} \times (\mathbf{Ax}_{i}))^{\intercal}(\mathbf{x}_{i}^{\prime}\times \mathbf{e}^{\prime}) / \| \mathbf{x}_{i}^{\prime} \times \mathbf{e}^{\prime} \|
\end{aligned}
\end{equation}
5.2.3. Proof
Canonical 카메라 행렬 $\mathbf{P}=[\mathbf{I}\ | \ 0], \mathbf{P}^{\prime}=[\mathbf{A}\ | \ \mathbf{e}^{\prime}]$일 때 Fundmaental Matrix $\mathbf{F}=\mathbf{e}^{\prime \wedge}\mathbf{A}$와 같이 구할 수 있고 이 때 $\mathbf{e}^{\prime\wedge}\mathbf{F} = \mathbf{e}^{\prime\wedge}\mathbf{e}^{\prime\wedge}\mathbf{A}$가 되어서
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime\wedge}\mathbf{F} = \mathbf{e}^{\prime\wedge}\mathbf{e}^{\prime\wedge}\mathbf{A} \sim \mathbf{A}
\end{aligned}
\end{equation}
와 같이 $\mathbf{A}$와 비례 관계가 된다. 따라서 $\mathbf{A} = \mathbf{e}^{\prime\wedge}\mathbf{F}$가 성립한다.
월드 상의 평면 $\pi=(\mathbf{v}^{\intercal},d)^{\intercal}$이 주어졌을 때 임의의 Homography $\mathbf{H}$는 $\mathbf{H}=\mathbf{A}-\mathbf{e}^{\prime}\mathbf{v}$와 같이 나타낼 수 있고 이 때 $\mathbf{v}$를 구하기 위해
\begin{equation}
\begin{aligned}
\mathbf{x}_{i}^{\prime} \times \mathbf{H}\mathbf{x}_{i} = 0
\end{aligned}
\end{equation}
식을 세운 후 정리하면
\begin{equation}
\begin{aligned}
& \mathbf{x}_{i}^{\prime} \times \mathbf{H}\mathbf{x}_{i} = 0 \\
& \mathbf{x}_{i}^{\prime} \times (\mathbf{A}\mathbf{x}_{i} - \mathbf{e}^{\prime}\mathbf{v}^{\intercal}\mathbf{x}_{i}) = 0 \\
& \mathbf{x}_{i}^{\prime} \times \mathbf{A}\mathbf{x}_{i} = (\mathbf{x}_{i} \times \mathbf{e}^{\prime})\mathbf{v}^{\intercal}\mathbf{x}_{i} \\
\end{aligned}
\end{equation}
꼴이 된다. 양변에 $(\mathbf{x}_{i} \times \mathbf{e}^{\prime})^{\intercal}$을 곱한 후 정리하면
\begin{equation}
\begin{aligned}
\mathbf{x}_{i}^{\intercal}\mathbf{v} = \mathbf{b}_{i}
\end{aligned}
\end{equation}
형태가 나온다. 이를 세 개의 점에 대해 모두 적용하면
\begin{equation}
\begin{aligned}
\begin{bmatrix} \mathbf{x}_{1}\\\mathbf{x}_{2}\\\mathbf{x}_{3} \end{bmatrix}\mathbf{v} = \begin{bmatrix} \mathbf{b}_{1}\\\mathbf{b}_{2}\\\mathbf{b}_{3} \end{bmatrix}
\end{aligned}
\end{equation}
가 된다 이 때, $\begin{bmatrix} \mathbf{x}_{1}\\\mathbf{x}_{2}\\\mathbf{x}_{3} \end{bmatrix}$를 행렬 $\mathbf{M}$으로 치환하면
\begin{equation}
\begin{aligned}
\mathbf{M}\mathbf{v} = \mathbf{b}
\end{aligned}
\end{equation}
꼴이 되고 이를 정리하면 결론적으로 $\mathbf{v} = \mathbf{M}^{-1}\mathbf{b}$가 된다. 이에 따라 Homography $\mathbf{H}$는 $\mathbf{H} = \mathbf{A} - \mathbf{e}^{\prime}(\mathbf{M}^{-1}\mathbf{b})^{\intercal}$과 같이 나타낼 수 있다.
5.2.4. A point and line

해당 섹션에서는 월드 상에 하나의 선과 하나의 점이 주어졌을 때 Homography $\mathbf{H}$를 구하는 방법에 대해 설명한다.
5.2.5. Result 13.7
월드 상에 직선 $\mathbf{L}$에 대응하는 이미지 평면 상에 대응선 쌍 $\mathbf{l} \leftrightarrow \mathbf{l}^{\prime}$이 주어졌을 때 월드 상의 직선 $\mathbf{L}$을 사용하여 $\mathbf{l}$을 $\mathbf{l}^{\prime}$로 변환하는 Homography $\mathbf{H}$는
\begin{equation}
\begin{aligned}
\mathbf{H}(\mu) = \mathbf{l}^{\prime \wedge}\mathbf{F} + \mu \mathbf{e}^{\prime}\mathbf{l}^{\intercal}
\end{aligned}
\end{equation}
과 같이 나타낼 수 있다. 이 때, $\mathbf{l}^{\prime \intercal}\mathbf{e}^{\prime} \neq 0$이어야 하며 $\mu$는 $\mu \in \mathbb{P}^{1}$인 파라미터이다.
5.2.6. Proof
카메라 행렬 대응쌍 $\mathbf{P} = [\mathbf{I} \ | \ 0], \mathbf{P}^{\prime}=[\mathbf{A} \ | \ \mathbf{e}^{\prime}]$이 주어졌을 때 이미지 평면 상의 직선 $\mathbf{l}, \mathbf{l}^{\prime}$을 Back-projection한 평면 $\pi_{\mathbf{l}} = \mathbf{P}^{\intercal}\mathbf{l}, \pi_{\mathbf{l}^{\prime}} = \mathbf{P}^{\prime\intercal}\mathbf{l}^{\prime}$과 같이 나타낼 수 있다. 두 개의 Back-projection 평면들은 $\pi_{\mathbf{l}},\ \pi_{\mathbf{l}^{\prime}}$이 교차하는 선이 월드 상의 직선 $\mathbf{L}$이 되고 이 때 $\mathbf{L}$을 포함하는 평면 $\pi$는
\begin{equation}
\begin{aligned}
\pi(\mu) & = \mu \mathbf{P}^{\intercal}\mathbf{l} + \mathbf{P}^{\prime \intercal}\mathbf{l}^{\prime}\\
& = \mu \begin{pmatrix} \mathbf{l}\\0 \end{pmatrix} + \begin{pmatrix} \mathbf{A}^{\intercal}\mathbf{l}^{\prime} \\ \mathbf{e}^{\prime \intercal}\mathbf{l}^{\prime} \end{pmatrix} \\
& = \begin{pmatrix} \mu \mathbf{l} + \mathbf{A}^{\intercal}\mathbf{l}^{\prime} \\ \mathbf{e}^{\prime \intercal}\mathbf{l}^{\prime} \end{pmatrix}
\end{aligned}
\end{equation}
과 같이 $\mu$로 파라미터화하여 $\mathbf{L}$을 포함하는 무수한 평면을 나타낼 수 있다. Result 13.1로부터 평면 $\pi(\mu)$를 사용한 Homography $\mathbf{H}$는
\begin{equation}
\begin{aligned}
\mathbf{H}(\mu) = \mathbf{A} - \mathbf{e}^{\prime}\mathbf{v}(\mu)^{\intercal}
\end{aligned}
\end{equation}
과 같이 나타낼 수 있고 이 때, $\mathbf{v}$는 위에서 설명한 $\pi(\mu)$ 공식에 따라 $\mathbf{v}(\mu) = (\mu\mathbf{l} + \mathbf{A}^{\intercal}\mathbf{l}^{\prime})/(\mathbf{e}^{\prime \intercal}\mathbf{l}^{\prime})$이 된다. 위 공식에 행렬 $\mathbf{A}$에 $\mathbf{A} = \mathbf{e}^{\prime\wedge}\mathbf{F}$를 대입하여 다시 정리하면
\begin{equation}
\begin{aligned}
\mathbf{H}(\mu) = -(\mathbf{l}^{\prime\wedge}\mathbf{F} + \mu \mathbf{e}^{\prime}\mathbf{l}^{\intercal}) / (\mathbf{e}^{\prime \intercal}\mathbf{l}^{\prime}) \sim \mathbf{l}^{\prime\wedge}\mathbf{F} + \mu \mathbf{e}^{\prime}\mathbf{l}^{\intercal}
\end{aligned}
\end{equation}
이 된다. 따라서 $\mathbf{H}$는 따라서 $\mathbf{H}(\mu) = \mathbf{l}^{\prime \wedge}\mathbf{F} + \mu \mathbf{e}^{\prime}\mathbf{l}^{\intercal}$에 비례하므로 해당 식과 같이 쓸 수 있다.
5.2.7. The homography for a corresponding point and line
앞서 설명한 대응선 쌍 $\mathbf{l} \leftrightarrow \mathbf{l}^{\prime}$을 이용한 Homography $\mathbf{H}(\mu)$는 $\mu$ 값에 따라 Homography가 변하는 특징이 있다.
5.2.8. Result 13.8
하나의 대응선 쌍 $\mathbf{l} \leftrightarrow \mathbf{l}^{\prime}$과 하나의 대응점 쌍 $\mathbf{x} \leftrightarrow \mathbf{x}^{\prime}$이 주어지면 이를 통해 $\mu$ 값을 특정되어 다음과 같은 유일한 Homography $\mathbf{H}$가 도출된다.
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{l}^{\prime\wedge}\mathbf{F} + \frac{(\mathbf{x}^{\prime}\times \mathbf{e}^{\prime})^{\intercal}(\mathbf{x}^{\prime}\times((\mathbf{Fx})\times \mathbf{l}^{\prime}))}{\| \mathbf{x}^{\prime}\times \mathbf{e}^{\prime} \|^{2}(\mathbf{l}^{\intercal}\mathbf{x})}\mathbf{e}^{\prime}\mathbf{l}^{\intercal}
\end{aligned}
\end{equation}
대응선 쌍 $\mathbf{l} \leftrightarrow \mathbf{l}^{\prime}$를 사용하면 월드 상의 평면 $\pi(\mu)$를 통해 $\mathbf{H}(\mu) = \mathbf{l}^{\prime \wedge}\mathbf{F} + \mu \mathbf{e}^{\prime}\mathbf{l}^{\intercal}$와 같이 Homography를 구할 수 있다. 이 때, $\mathbf{Hx} = \mathbf{x}^{\prime}$ 식을 통해 $\mathbf{x}^{\prime}\times(\mathbf{Hx}) = 0$ 식을 전개해보면
\begin{equation}
\begin{aligned}
& \mathbf{x}^{\prime} \times (\mathbf{l}^{\prime\wedge}\mathbf{Fx} + \mu \mathbf{e}^{\prime}\mathbf{l}^{\intercal}\mathbf{x}) = 0 \\
\end{aligned}
\end{equation}
이 된다. 이를 전개 후 정리해보면
\begin{equation}
\begin{aligned}
(\mathbf{x}^{\prime}\times \mathbf{e}^{\prime})\mathbf{l}^{\intercal}\mathbf{x} \cdot \mu & = -\mathbf{x}^{\prime} \times \mathbf{l}^{\prime} \times \mathbf{Fx} \\
& = \mathbf{x}^{\prime} \times \mathbf{Fx} \times \mathbf{l}^{\prime}
\end{aligned}
\end{equation}
이 되고 양변에 $(\mathbf{x}^{\prime}\times \mathbf{e}^{\prime})^{\intercal}$을 곱하여 $\mu$에 대하여 정리 후 $\mathbf{H}(\mu)$식 에 넣어주면
\begin{equation}
\begin{aligned}
\mathbf{H} = \mathbf{l}^{\prime\wedge}\mathbf{F} + \frac{(\mathbf{x}^{\prime}\times \mathbf{e}^{\prime})^{\intercal}(\mathbf{x}^{\prime}\times((\mathbf{Fx})\times \mathbf{l}^{\prime}))}{\| \mathbf{x}^{\prime}\times \mathbf{e}^{\prime} \|^{2}(\mathbf{l}^{\intercal}\mathbf{x})}\mathbf{e}^{\prime}\mathbf{l}^{\intercal}
\end{aligned}
\end{equation}
공식을 얻을 수 있다.
5.3. Computing $\mathbf{F}$ given the homography induced by a plane

일반적으로 두 개의 카메라 행렬 대응쌍 $(\mathbf{P},\mathbf{P}^{\prime})$에 대한 Fundamental Matrix $\mathbf{F}$를 계산하기 위해서는 최소 8개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}), \ i=1,\cdots,8$이 필요하다. 하지만 Scene Plane Homography를 이용하면 6개의 대응점 쌍만 사용해도 $\mathbf{F}$를 계산할 수 있다. 단, 6개의 대응점 쌍들 중 4개 대응점 쌍 $(\mathbf{x}_{i}, \mathbf{x}_{i}^{\prime}), \ i=1,\cdots,4$에 해당하는 월드 상의 점들의 동일한 평면 $\pi$ 위에 존재해야 한다는 제약조건이 있다.
6개의 대응점 쌍으로 Fundmaental Matrix $\mathbf{F}$를 계산하는 알고리즘의 순서는 다음과 같다.
- 월드 상의 평면 $\pi$ 위에 존재하는 4개의 점들 $\mathbf{X}_{i},\ i=1,\cdots,4$를 프로젝션한 대응점 쌍들 $(\mathbf{x}_{i}, \mathbf{x}_{i}^{\prime}), \ i=1,\cdots,4$를 사용하여 $\mathbf{x}_{i}^{\prime} = \mathbf{H}\mathbf{x}_{i}$를 만족하는 Homorgaphy $\mathbf{H}$를 계산한다. 이 때 4쌍의 대응점은 Homography $\mathbf{H}$를 유일하게 결정한다.
- 남은 2개의 대응점 쌍 $(\mathbf{x}_{i}, \mathbf{x}_{i}^{\prime}),\ i=5,6$을 사용하여 Epipole $\mathbf{e}^{\prime}$를 구한다. $\mathbf{x}_{5}$를 Homography 변환한 $\mathbf{Hx}_{5}$와 $\mathbf{x}_{5}^{\prime}$를 사용하여 두 점을 잇는 직선을 $(\mathbf{Hx}_{5})\times \mathbf{x}_{5}^{\prime}$와 같이 구한다. $\mathbf{x}_{6}$에 대해서도 마찬가지로 적용하여 직선 $(\mathbf{Hx}_{6})\times \mathbf{x}_{6}^{\prime}$를 구한 다음 두 직선이 교차하는 점을 구하면 그 점이 곧 Epipole $\mathbf{e}^{\prime}$가 된다.
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime} = (\mathbf{Hx}_{5}) \times \mathbf{x}_{5}^{\prime} \cap (\mathbf{Hx}_{6}) \times \mathbf{x}_{6}^{\prime}
\end{aligned}
\end{equation}
- Fundamental Matrix $\mathbf{F}$를 $\mathbf{F}=\mathbf{e}^{\prime\wedge}\mathbf{H}$를 통해 구한다.
5.4. The infinite homography $\mathbf{H}_{\infty}$

5.4.1. Definition 13.10
Scene Plane이 무한대 평면(plane at infinity) $\pi_{\infty}$인 경우, 이 때 계산한 Homography를 Infinity Homography $\mathbf{H}_{\infty}$라고 한다.
카메라 행렬 대응쌍 $(\mathbf{P}, \mathbf{P}^{\prime})$가 다음과 같이 주어졌을 때
\begin{equation}
\begin{aligned}
& \mathbf{P} = \mathbf{K}[\mathbf{I} \ |\ 0 ] & \mathbf{P}^{\prime} = \mathbf{K}^{\prime}[\mathbf{R} \ |\ \mathbf{t} ] \\
\end{aligned}
\end{equation}
월드 상의 평면 $\pi(d) = \begin{pmatrix} \mathbf{v} \\ d \end{pmatrix}$에 대해 Homography는 다음과 같이 구할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{H}_{\pi(d)} = \mathbf{K}^{\prime}(\mathbf{R}-\frac{\mathbf{tn}^{\intercal}}{d})\mathbf{K}^{-1}
\end{aligned}
\end{equation}
Inifinite Homography $\mathbf{H}_{\infty}$는 $d$가 무한대인 경우에 해당하므로
\begin{equation}
\begin{aligned}
\mathbf{H}_{\infty} = \lim_{d\rightarrow \infty} \mathbf{H}_{\pi(d)} = \mathbf{K}^{\prime}\mathbf{RK}^{-1}
\end{aligned}
\end{equation}
가 된다. 따라서 $\mathbf{H}_{\infty}$는 $\mathbf{t}$에 의존하지 않고 오직 카메라의 회전에만 의존한다는 것을 알 수 있다.
5.4.2. Affine and metric reconstruction
만약 월드좌표계가 Affine인 경우 $\pi_{\infty}$는 $\pi_{\infty}=(0,0,0,1)^{\intercal}$과 같이 나타낼 수 있고 두 카메라 행렬이 $\mathbf{P}=[\mathbf{M}\ | \ \mathbf{m}], \ \mathbf{P}^{\prime}=[\mathbf{M}^{\prime} \ | \ \mathbf{m}^{\prime}]$으로 주어진 경우 무한대 평면 상의 점 $\mathbf{X} \in \pi_{\infty}$를 각각 카메라에 프로젝션하면
\begin{equation}
\begin{aligned}
& \mathbf{x} = \mathbf{PX} = [\mathbf{M} \ | \ \mathbf{m}] \begin{bmatrix} \tilde{\mathbf{X}} \\ 0 \end{bmatrix} = \mathbf{M}\tilde{\mathbf{X}} \\
& \mathbf{x}^{\prime} = \mathbf{P}^{\prime}\mathbf{X} = [\mathbf{M}^{\prime} \ | \ \mathbf{m}^{\prime}] \begin{bmatrix} \tilde{\mathbf{X}} \\ 0 \end{bmatrix} = \mathbf{M}^{\prime}\tilde{\mathbf{X}} = (\mathbf{\mathbf{M}^{\prime}\mathbf{M}^{-1}})\mathbf{x} \\
\end{aligned}
\end{equation}
따라서 $\mathbf{x}^{\prime} = (\mathbf{M}^{\prime}\mathbf{M}^{-1})\mathbf{x}$가 되어 월드좌표계가 Affine일 때 두 카메라 사이의 Infinite Homography는 $\mathbf{H}_{\infty} = \mathbf{M}^{'}\mathbf{M}^{-1}$가 된다.
----------
6. Affine Epipolar Geometry

핀홀 카메라(pinhole camera)는 월드 상의 물체가 이미지 평면 상에 프로젝션될 때 초점이라 부르는 하나의 점을 통과하여 이미지 평면상에 투과되는 카메라 모델을 의미한다. 따라서 핀홀 카메라 모델은 사영공간(projective space) $\mathbb{P}^{3} \mapsto \mathbb{P}^{2}$로 매핑하는 함수로 모델링 할 수 있고 원근법에 의한 왜곡이 발생한다. 이와 반대로 Affine 카메라는 월드 상의 물체가 이미지 평면 상에 프로젝션 될 때 마치 무한대 광원에 의한 그림자 상이 맺히는 것과 같이 이미지 평면에 프로젝션되는 카메라를 의미한다. 따라서 Affine 카메라는 원근법에 의한 왜곡이 발생하지 않는다.
Affine 카메라도 Canonical Form으로 나타낼 수 있다. 두 개의 Affine 카메라 $\mathbf{P}_{A}, \mathbf{P}_{A}^{\prime}$가 주어졌을 때 월드 좌표계와 카메라 좌표계가 동일한 경우 $\mathbf{P}_{A}$의 주축(principal axis)는 $Z$축이 되고 이 때의 프로젝션은 $XY$ 평면으로 프로젝션이 된다. 그리고 $\mathbf{P}_{A}^{\prime}$는 Affine 변환 $\mathbf{M}$과 카메라 이동 $\mathbf{t}$를 통해 표현할 수 있다. 이 때, 두 개의 Affine 카메라는 모두 마지막 행(row)이 $(0,0,0,1)$인 성질을 지닌다.
\begin{equation}
\begin{aligned}
\mathbf{P}_{A} & = \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&0&1 \end{bmatrix} & \mathbf{P}_{A}^{\prime} & = \begin{bmatrix} \mathbf{M} & \mathbf{t} \\ \mathbf{0} & 1\end{bmatrix} \quad \text{where, } \mathbf{M} \in \mathbb{R}^{2\times 3},\ \mathbf{t} \in \mathbb{R}^{2}
\end{aligned}
\end{equation}
Affine 카메라 행렬 $\mathbf{P}_{A}$는 Affine 변환의 특성 상 무한대 평면(plane at infinity) $\pi_{\infty}=(X,Y,Z,0)^{\intercal}$ 상의 한 점을 무한대 직선(line at infinity) $\mathbf{l}_{\infty}$ 상의 한 점으로 변환한다. 즉, 월드 상 물체의 평행한 성질이 보존된다.
\begin{equation}
\begin{aligned}
\mathbf{P}_{A} \begin{bmatrix} X\\Y\\Z\\0 \end{bmatrix} = \begin{bmatrix} \ast \\ \ast \\ 0 \end{bmatrix} \in \mathbf{l}_{\infty}
\end{aligned}
\end{equation}
일반적인 Affine 카메라 행렬 $\begin{bmatrix} \mathbf{M} & \mathbf{m} \\ \mathbf{0} & 1 \end{bmatrix} \in \mathbb{R}^{3\times 4}$에서 행렬 $\mathbf{M} \in \mathbb{R}^{2\times 3}$의 rank는 2이므로
\begin{equation}
\begin{aligned}
\mathbf{M}\tilde{\mathbf{C}} = 0
\end{aligned}
\end{equation}
을 만족하는 Affine 카메라의 중심점 $\mathbf{C}$이 존재한다. 이 때, $\mathbf{C}$는 무한대 평면 상에 존재한다.
\begin{equation}
\begin{aligned}
\mathbf{C} = \begin{pmatrix} \tilde{\mathbf{C}} \\ 0 \end{pmatrix} \in \pi_{\infty}
\end{aligned}
\end{equation}
Affine 카메라 행렬 $\mathbf{P}_{A}$의 중심점 $\mathbf{C}$는 $\mathbf{C} = \begin{bmatrix} 0&0&1&0 \end{bmatrix}^{\intercal}$이다. 즉, Affine 카메라의 중심점은 주축(principal axis)의 방향과 동일하다.
6.1. Affine epipolar geometry

6.1.1. Epipolar lines
두 개의 동일한 Affine 카메라가 주어졌을 때, 이들의 Back-projection 직선을 생각해보자. 첫 번째 Affine 카메라의 이미지 평면 상의 한 점 $\mathbf{x}$를 Back-projection하면
\begin{equation}
\begin{aligned}
\mathbf{X}(\lambda) = \mathbf{P}_{A}^{\dagger}\mathbf{x} + \lambda \begin{bmatrix} \tilde{\mathbf{C}} \\ 0 \end{bmatrix}
\end{aligned}
\end{equation}
이 되므로 Back-projection 직선들의 방향이 곧 Affine 카메라의 중심점 방향 $\begin{bmatrix} \tilde{\mathbf{C}} \\ 0 \end{bmatrix}$이 된다. 즉, Affine 카메라의 이미지 평면 상 모든 점들의 Back-projection 직선들은 평행하므로 이를 두 번째 Affine 카메라에 프로젝션한 Epipolar Line들 또한 모두 평행하다.
6.1.2. The epipoles
Epipolar Line들이 모두 평행하므로 Epipole들은 모두 무한대 직선(line at infinity) 상에 존재한다.
6.2. The affine fundamental matrix
6.2.1. Result 14.1
두 개의 동일한 Affine 카메라가 주어졌을 때 이를 통해 Affine Fundamental Matrix $\mathbf{F}_{A}$를 정의할 수 있다. 이 때, $\mathbf{F}_{A}$는
\begin{equation}
\begin{aligned}
\mathbf{F}_{A} = \begin{bmatrix} 0&0&\ast \\ 0&0&\ast \\ \ast&\ast&\ast \end{bmatrix}
\end{aligned}
\end{equation}
꼴로 나타난다. $\ast$는 0이 아닌 값을 의미한다. 일반적으로 $\mathbf{F}_{A}$는
\begin{equation}
\begin{aligned}
\mathbf{F}_{A} = \begin{bmatrix} 0&0&a \\ 0&0&b \\ c&d&e \end{bmatrix}
\end{aligned}
\end{equation}
와 같이 작성한다. $\mathbf{F}_{A}$는 일반적인 Fundamental Matrix와 동일하게 rank 2를 가진다.
6.2.2. Derivation
6.2.3. Geometric derivation
두 개의 Affine 카메라 행렬 $\mathbf{P}_{A}, \mathbf{P}_{A}^{\prime}$가 주어졌을 때 둘 사이에는 Affine 변환의 성질에 의해 평행한 선들이 보존된다. 따라서 두 이미지 평면의 Homography $\mathbf{H}_{A}$는 Affine Homography가 되어
\begin{equation}
\begin{aligned}
& \mathbf{x}^{\prime} = \mathbf{H}_{A} \mathbf{x} \quad \text{where, } \mathbf{H}_{A} = \begin{bmatrix} \ast&\ast&\ast \\ \ast&\ast&\ast \\ 0&0&1 \end{bmatrix}
\end{aligned}
\end{equation}
을 만족한다. Affine 카메라의 Epipole $\mathbf{e}^{\prime}$은 무한대 직선(line at infinity) 상에 존재하므로 $\mathbf{e}^{\prime}$의 Cross Product는
\begin{equation}
\begin{aligned}
\mathbf{e}^{\prime\wedge} = \begin{bmatrix} 0&0&\ast \\ 0&0&\ast \\ \ast&\ast&0 \end{bmatrix}
\end{aligned}
\end{equation}
꼴이다. Affine Fundamental Matrix $\mathbf{F}_{A}$는 $\mathbf{F}_{A} = \mathbf{e}^{\prime\wedge}\mathbf{H}_{A}$를 통해 계산할 수 있으므로
\begin{equation}
\begin{aligned}
\mathbf{F}_{A} & = \mathbf{e}^{\prime \wedge}\mathbf{H}_{A} \\
& = \begin{bmatrix} 0&0&\ast \\ 0&0&\ast \\ \ast&\ast&0 \end{bmatrix} \begin{bmatrix} \ast&\ast&\ast \\ \ast&\ast&\ast \\ 0&0&1 \end{bmatrix} = \begin{bmatrix} 0&0&\ast \\ 0&0&\ast \\ \ast&\ast&\ast \end{bmatrix}
\end{aligned}
\end{equation}
와 같은 형태가 된다.
6.2.4. Properties
6.2.5. The epipoles
Affine Fundamental Matrix $\mathbf{F}_{A}$가 주어졌을 때 이를 통해 Epipole $\mathbf{e}, \mathbf{e}^{\prime}$를 계산할 수 있다. $\mathbf{F}_{A}$가
\begin{equation}
\begin{aligned}
& \mathbf{F}_{A} = \begin{bmatrix} 0&0&a \\ 0&0&b \\ c&d&e \end{bmatrix} \\
\end{aligned}
\end{equation}
일 때 Fundamental Matrix의 성질로 인해 $\mathbf{F}_{A}\mathbf{e} = 0$와 $\mathbf{e}^{\prime \intercal}\mathbf{F}_{A} = 0$가 성립하므로 다음과 같이 계산할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{e} = \begin{bmatrix} -d & c & 0 \end{bmatrix}^{\intercal}\\
& \mathbf{e}^{\prime} = \begin{bmatrix} -b & a & 0 \end{bmatrix}^{\intercal}
\end{aligned}
\end{equation}
6.2.6. Epipolar lines
첫 번째 Affine 이미지 평면 상의 점 $\mathbf{x}$와 Affine Fundamental Matrix $\mathbf{F}_{A}$가 주어졌을 때 두 번째 Affine 이미지 평면 상의 Epipolar Line $\mathbf{l}^{\prime}$는 다음과 같이 계산할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{x} = \begin{pmatrix} x&y&1 \end{pmatrix}^{\intercal} \\
& \mathbf{F}_{A} = \begin{bmatrix} 0&0&a \\ 0&0&b \\ c&d&e \end{bmatrix} \\
& \mathbf{l}^{\prime} = \mathbf{F}_{A}\mathbf{x} = \begin{pmatrix} a & b & cx+dy+e \end{pmatrix}^{\intercal}
\end{aligned}
\end{equation}
Epipolar Line $\mathbf{l}^{\prime}$의 처음 두 개의 항 $(a,b)$가 이미지 평면 상의 점 $\mathbf{x}=(x,y,1)^{\intercal}$에 독립적이므로 이는 곧 $\mathbf{x}$에 관계없이 Epipolar Line들이 평행하다는 것을 의미한다.
6.3. Estimating $\mathbf{F}_{A}$ from image point correspondences

Projective 카메라의 Fundamental Matrix $\mathbf{F}$를 계산하기 위해서는 두 이미지 평면 사이에 대응점 쌍 $(\mathbf{x},\mathbf{x}^{\prime})$가 최소 8개 이상이 필요하다. 하지만 Affine 카메라의 Affine Fundamental Matrix $\mathbf{F}_{A}$는 앞서 설명한 것과 같이 좌상단 $2\times 2$ 항이 0이므로 최소 4개 이상의 대응점 쌍 $(\mathbf{x}, \mathbf{x}^{\prime})$만으로도 $\mathbf{F}_{A}$를 구할 수 있다.
6.3.1. Algorithm 14.2
- Objective: Affine 이미지 평면에서 4개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}),\ i=1,\cdots,4$가 주어졌을 때 이를 통해 Affine Fundamental Matrix를 구한다.
- 우선 처음 세 개의 대응점 쌍 $(\mathbf{x}_{i},\mathbf{x}_{i}^{\prime}),\ i=1,2,3$을 Back-projection함으로써 월드 상의 점 $\mathbf{X}_{i},\ i=1,2,3$을 구할 수 있고 이 점들을 Span함으로써 유일한 평면 $\pi$가 결정할 수 있다.
\begin{equation}
\begin{aligned}
\pi = \text{Span}\{ \mathbf{X}_{1}, \mathbf{X}_{2}, \mathbf{X}_{3} \}
\end{aligned}
\end{equation}
- 월드 상의 평면 $\pi$에 대해 $\mathbf{x}^{\prime} = \mathbf{H}_{A}\mathbf{x}$를 만족하는 Affine Homography $\mathbf{H}_{A}$를 구한다. 일반적으로 Homography를 구하기 위해서는 네 개 이상의 대응점 쌍이 필요하지만 Affine Homography는 마지막 행이 항상 $(0,0,1)$이므로 세 개의 대응점 쌍을 통해서도 $\mathbf{H}_{A}$를 계산할 수 있다.
- 나머지 한 점 $\mathbf{x}_{4}$를 사용하여 $\mathbf{H}_{A}\mathbf{x}_{4}$와 $\mathbf{x}_{4}$를 잇는 Epipolar Line $\mathbf{l}^{\prime}$을 계산한다.
\begin{equation}
\begin{aligned}
\mathbf{l}^{\prime} = \mathbf{H}_{A}\mathbf{x}_{4} \times \mathbf{x}^{\prime}_{4}
\end{aligned}
\end{equation}
Epipolar Line $\mathbf{l}^{\prime}$를 계산했으면 이를 통해 Epipole $\mathbf{e}^{\prime} = (-l_{2}^{\prime},l_{1}^{\prime},0)^{\intercal}$를 계산할 수 있다. 만약 $\mathbf{x}_{4}$를 Back-projection한 월드 상의 점 $\mathbf{X}_{4}$가 월드 상의 평면 $\pi$ 위에 존재하는 경우 Epipolar Line을 구할 수 없다.
- $\mathbf{F}_{A} = \mathbf{e}^{\prime\wedge}\mathbf{H}_{A}$를 통해 Affine Fundamental Matrix를 계산한다.
\begin{equation}
\begin{aligned}
\mathbf{F}_{A} = \begin{bmatrix} -l_{2}^{\prime}&l_{1}^{\prime}&0 \end{bmatrix}^{\intercal\wedge}\mathbf{H}_{A}
\end{aligned}
\end{equation}
7 References
'Fundamental' 카테고리의 다른 글
| [SLAM] Pose Graph Optimization 개념 설명 및 예제 코드 분석 (20) | 2022.01.05 |
|---|---|
| 다중관점기하학(Multiple View Geometry in Computer Vision) 책 내용 정리 Part 3 (0) | 2022.01.05 |
| 다중관점기하학(Multiple View Geometry in Computer Vision) 책 내용 정리 Part 1 (5) | 2022.01.05 |
| Plücker Coordinate 개념 정리 (3) | 2022.01.05 |
| 선형대수학 (Linear Algebra) 개념 정리 Part 1 (1) | 2022.01.05 |
 A L I D A
A L I D A





