1. Introduction
Plücker Coordinate 표현법은 19세기 수학자 Julius Plücker에 의해 처음 소개되었다. 해당 표현법은 직선을 표현하는 방법 중 하나로 6차원 $\mathbb{P}^{5}$ 공간 상의 한 점을 사용하여 4차원 $\mathbb{P}^{3}$ 공간 상의 직선을 표현할 때 사용된다. 해당 표현법은 자체 제약조건으로 인해 $\mathbb{P}^{5}$ 곡면(quadric) 상의 한점과 $\mathbb{P}^{3}$ 공간 상의 직선이 일대일 대응을 이루는 특징이 있다. 사영 공간(projective space)에 대한 자세한 내용은 해당 포스팅을 참조하면 된다.
MVG 책에서는 일반적으로 3차원 공간 상의 점을 $\mathbf{X} = [X,Y,Z,W] \in \mathbb{P}^{3}$와 같이 나타내지만 Plücker Coordinates에서는 (\ref{eq:2})와 같이 $l_{ij}$ 인덱싱의 편의를 위해 $[W,X,Y,Z]$ 순서를 사용하기도 한다. $[X,Y,Z,W]$ 순서로 나타내면 (\ref{eq:3})과 같다. 따라서 이를 실제로 사용할 때는 순서에 유의하여야 한다.
컴퓨터 그래픽 분야에서 Plücker Coordinate 표현법이 자주 사용되며 로보틱스나 기구학에서도 Screw, Wrench를 표현할 때 해당 직선 표현법을 사용하는 등 종종 사용된다. 그리고 SLAM 분야에서도 직선을 활용할 때 Plücker Coordinate 표현법을 활용하여 특징선(line feature)을 트래킹하거나 최적화를 수행하는 연구 또한 볼 수 있다. [4][5]
NOMENCLATURE
- 3차원 공간 상의 Plücker 직선은 $\mathcal{L} \in \mathbb{P}^{5}$로 표기한다.
- 이미지 평면 상 직선은 $l \in \mathbb{P}^{2}$로 표기한다. 해당 포스트에서 $l$은 스칼라가 아님에 유의한다.
- Plücker 행렬은 $\mathbf{L} \in \mathbb{R}^{6\times 6}$로 표기한다. 이는 Plücker 직선이 아니라 6x6 행렬임에 유의한다.
- 이미지 평면 상 직선의 Plücker 행렬은 $\mathbf{l} \in \mathbb{R}^{3\times 3}$로 표기한다. 이는 직선이 아니라 3x3 행렬임에 유의한다.
- $(*)^{\wedge}$는 벡터 $*$의 반대칭행렬(skew-symmetric matrix)를 의미한다 e.g., $\mathbf{x} = \begin{bmatrix} x,y,z \end{bmatrix}^{\intercal}$일 때 $\mathbf{x}^{\wedge} = \begin{bmatrix} 0 & -z & y \\ z & 0 & -x \\ -y & x & 0 \end{bmatrix}$. 다른 문서에서는 $[*]_{\times}$로 표기하기도 한다.
2. How to represent a line in 3D space
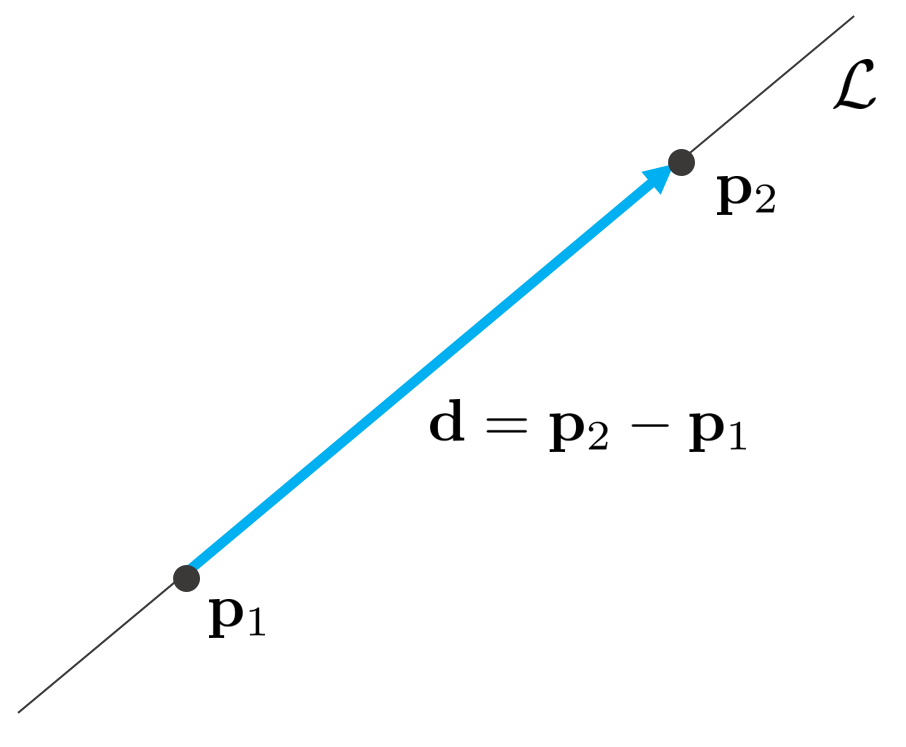
3차원 공간 상에서 직선을 표현하는 방법은 여러가지 방법들이 존재한다. 예를 들면 두 점 $\mathbf{p}_{1}, \mathbf{p}_{2}$을 사용함으로써 직선 $\mathcal{L}$을 표현할 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{L} (\mathbf{p}_{1}, \mathbf{p}_{2})
\end{aligned}
\end{equation}
또는 직선 위의 한 점 $\mathbf{p}_{1}$과 방향벡터 $\mathbf{d}$를 가지고 직선을 표현할 수 있다.
\begin{equation}
\begin{aligned}
& \mathcal{L} (\mathbf{p}_{1}, \mathbf{d}) \\
& \text{where, } \mathbf{d} = \mathbf{p}_{2} - \mathbf{p}_{1} \\
\end{aligned}
\end{equation}
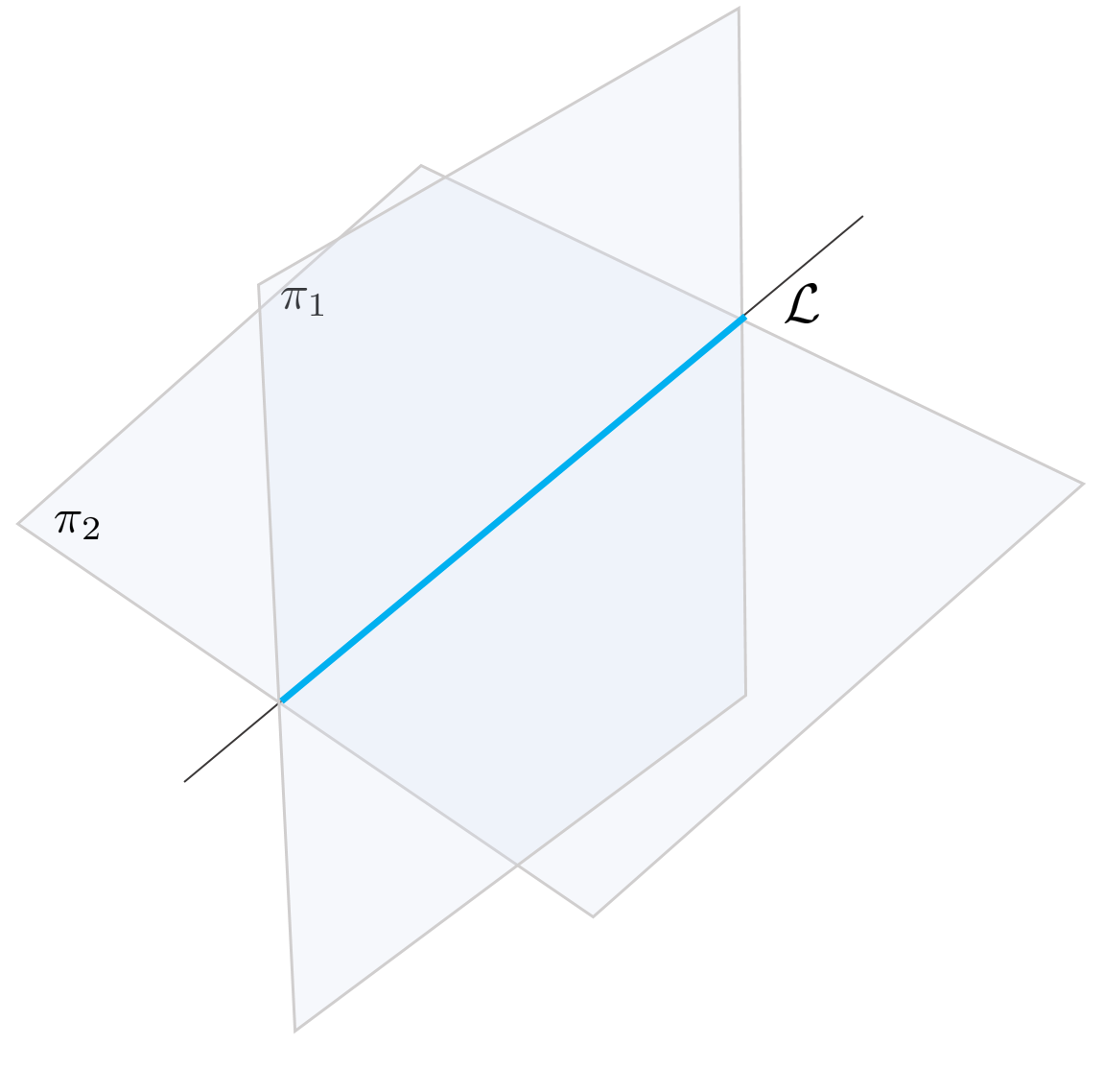
또는 평행하지 않은 두 평면 $\pi_{1}, \pi_{2}$의 교차선이 직선을 형성하므로 평면 2개를 통해 직선 $\mathcal{L}$을 표현할 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{L} (\pi_{1}, \pi_{2})
\end{aligned}
\end{equation}
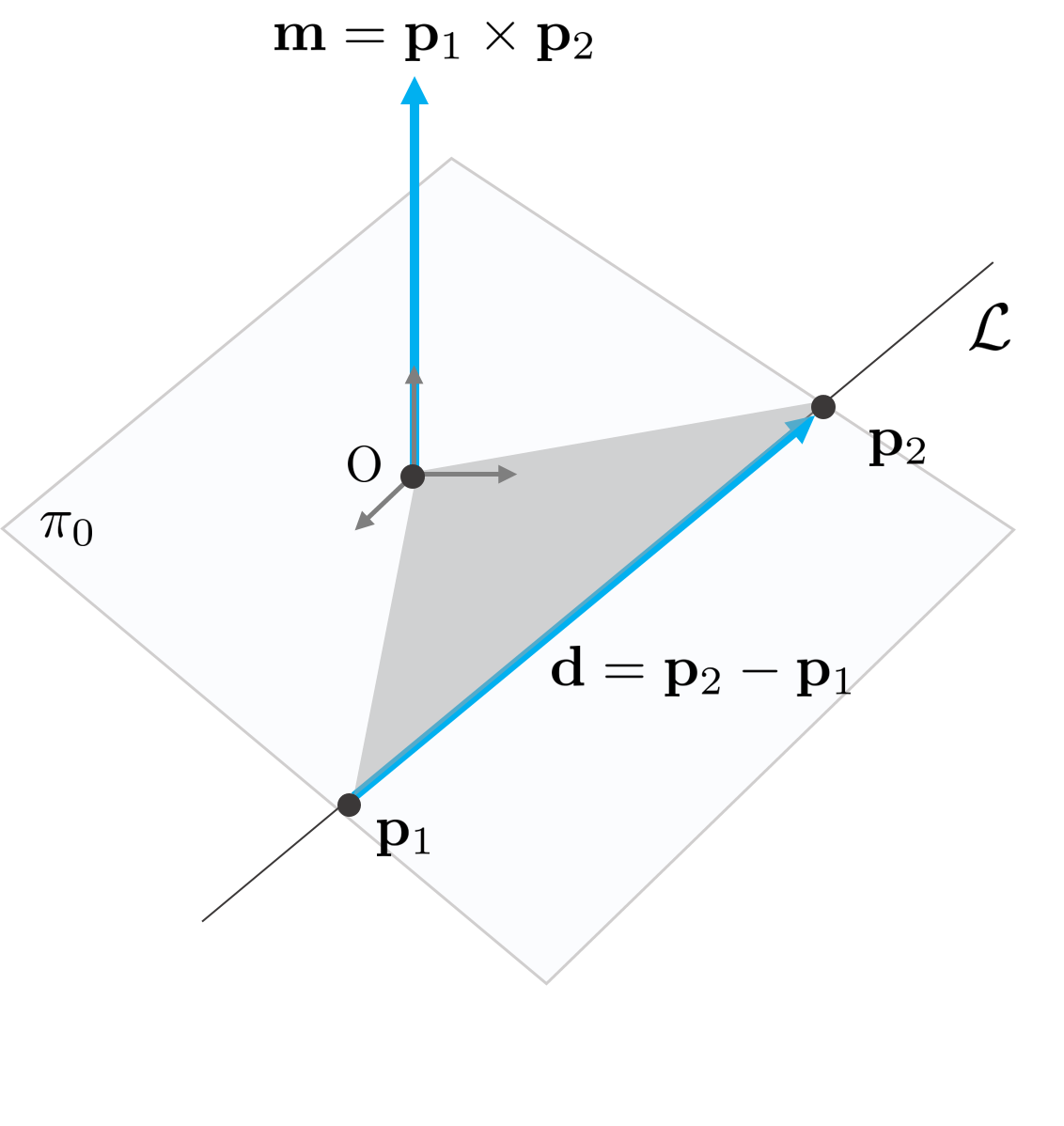
또는 직선의 방향벡터 $\mathbf{d}$와 원점을 포함하며 직선을 포함하는 평면 $\pi_{0}$의 방향벡터 $\mathbf{m}$을 사용하여 직선을 표현할 수 있다.
\begin{equation}
\begin{aligned}
& \mathcal{L} (\mathbf{d}, \mathbf{m}) \in \mathbb{P}^{5} \\
& \text{where, } \mathbf{d} = \mathbf{p}_{2} - \mathbf{p}_{1} \\
& \mathbf{m} = \mathbf{p}_{1} \times \mathbf{p}_{2}
\end{aligned}
\end{equation}
이 때, $\mathbf{m}$은 단위 질량을 가진 점 $\mathbf{p}_{1}$이 $\mathbf{p}_{2}$로 움직일 때 발생하는 모멘트 벡터로 생각할 수 있으며 모멘트 벡터의 크기는 $\mathbf{p}_{1}, \mathbf{p}_{2}$와 원점을 이은 삼각형의 넓이의 2배가 된다. 방향 벡터 $\mathbf{d}$와 모멘트 벡터 $\mathbf{m}$은 서로 직교하므로 다음 공식이 성립한다.
\begin{equation}
\begin{aligned}
& \mathbf{m}^{\intercal} \cdot \mathbf{d} = 0
\end{aligned} \label{eq:4}
\end{equation}
$\mathbf{d}$ 또는 $\mathbf{m}$ 중 하나만을 사용하면 직선 $\mathcal{L}$을 유일하게 표현할 수 없지만 $(\mathbf{d}, \mathbf{m})$ 쌍을 활용하면 스칼라 값에 무관한(up to scale) 유일한 직선을 표현할 수 있다.
\begin{equation}
\begin{aligned}
(\mathbf{d}:\mathbf{m}) = (d_{x}:d_{y}:d_{z}:m_{x}:m_{y}:m_{z})
\end{aligned}
\end{equation}
이러한 여러 직선 표현 방법들 중 $(\mathbf{d},\mathbf{m})$을 사용하여 직선을 표현하는 방법을 Plücker Coordinate 표현법이라고 한다. 해당 표현법은 homogeneous 표현법이기 때문에 0이 아닌 스칼라 $\lambda$에 대하여 $(\mathbf{d}:\mathbf{m}) = (\lambda\mathbf{d}:\lambda\mathbf{m})$를 만족한다.
3. Plücker coordinate representation
Plücker Coordinate에서 직선을 표현하는 방법은 다음과 같다. $\mathbb{P}^{3}$ 공간에 두 점 $\mathbf{p}_{1}, \mathbf{p}_{2}$가 존재할 때
\begin{equation}
\begin{aligned}
& \mathbf{p}_{1} = [W_{1}, X_{1}, Y_{1}, Z_{1}] \\
& \mathbf{p}_{2} = [W_{2}, X_{2}, Y_{2}, Z_{2}]
\end{aligned}
\end{equation}
와 같이 나타낼 수 있다. 설명의 편의를 위해 $[X, Y, Z, W] \rightarrow [W, X, Y, Z]$ 순으로 표기한다. 직선에 대한 방향벡터 $\mathbf{d} = \mathbf{p}_{2} - \mathbf{p}_{1}$과 원점과 직선을 포함하는 평면의 방향벡터 $\mathbf{m}=\mathbf{p}_{2}\times \mathbf{p}_{1}$이 있을 때 직선 $\mathcal{L}$은 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{L} = (\mathbf{d}:\mathbf{m}) = (d_{x}:d_{y}:d_{z}:m_{x}:m_{y}:m_{z})
\end{aligned}
\end{equation}
이 때, $\mathbf{m}$은 원점과 직선 사이의 모멘트(Moment) 벡터이며 만약 모멘트 벡터가 0이면 직선이 원점을 포함하고 있다는 의미이다. 위 식의 값을 유도하기 위해 아래와 같이 두 점을 행으로 하는 행렬 $\mathbf{M} \in \mathbb{R}^{2\times 4}$을 설정하고 2x2 submatrix에 대한 행렬식 연산 $l_{ij}$을 정의하면 다음과 같다.
\begin{equation}
\begin{aligned}
& \mathbf{M} = \begin{bmatrix} W_{1} & X_{1} & Y_{1} & Z_{1} \\ W_{2}&X_{2}&Y_{2}&Z_{2} \end{bmatrix} \\
& l_{ij} = \begin{vmatrix} X_{i} & Y_{i} \\ X_{j} & Y_{j} \end{vmatrix} = X_{i}Y_{j} - X_{j}Y_{i}
\end{aligned}
\end{equation}
$l_{ii}=0, l_{ij} = -l_{ji}$의 성질을 지닌다. 결론적으로 직선 $\mathcal{L}$은 다음과 같이 정의할 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{L} = (\mathbf{d}:\mathbf{m}) & = (d_{x}:d_{y}:d_{z}:m_{x}:m_{y}:m_{z}) \\ &= (l_{01}:l_{02}:l_{03}:l_{23}:l_{31}:l_{12})
\end{aligned} \label{eq:2}
\end{equation}
해당 직선 표현법은 스케일을 제외하고(up to scale) 유일하게 직선을 표현할 수 있으며 적어도 하나의 원소는 0이 아니어야 한다. 일반적으로 Plücker Coordinate는 homogeneous한 $\mathbb{P}^{5}$ 공간의 한 점을 콜론(:)을 사용하여 표현한다. 콜론(:)을 사용한 이유는 up to scale 특성 상 해당 여섯 원소들의 값 자체보다 원소들 사이의 비율이 중요하기 때문이다.
이 때, $l_{ij}$의 각 성분들을 자세히 표기하면 다음과 같다.
\begin{equation}
\begin{aligned}
& l_{01} = W_{1}X_{2}-W_{2}X_{1} & l_{23} = Y_{1}Z_{2}-Z_{1}Y_{2} \\
& l_{02} = W_{1}Y_{2}-W_{2}Y_{1} &l_{31} = Z_{1}X_{2}-X_{1}Z_{2} \\
& l_{03} = W_{1}Z_{2}-W_{2}Z_{1} & l_{12} = X_{1}Y_{2}-Y_{1}X_{2}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\mathbf{d} = \begin{bmatrix} W_{1}X_{2}-W_{2}X_{1} \\
W_{1}Y_{2}-W_{2}Y_{1} \\
W_{1}Z_{2}-W_{2}Z_{1} \end{bmatrix} \quad \quad
\mathbf{m} = \begin{bmatrix} Y_{1}Z_{2}-Z_{1}Y_{2} \\
Z_{1}X_{2}-X_{1}Z_{2} \\
X_{1}Y_{2}-Y_{1}X_{2} \end{bmatrix}
\end{aligned}
\end{equation}
이 때, 위 식에서 $\mathbf{m} = \mathbf{p}_{1} \times \mathbf{p}_{2}$과 같은 것을 알 수 있다. 만약 $W_{1}=W_{2}=1$이면 $l_{01}, l_{02}, l_{03}$은 다음과 같이 간결하게 나타낼 수 있다.
\begin{equation}
\begin{aligned}
l_{01} = X_{2}-X_{1} \quad l_{02} = Y_{2}-Y_{1} \quad l_{03} = Z_{2}-Z_{1}
\end{aligned}
\end{equation}
이는 $\mathbf{d} = \mathbf{p}_{2} - \mathbf{p}_{1}$의 정의와 동일하다.
3.1. Graßmann–Plücker relations
Plücker Coordinates 표현법은 Graßmann–Plücker relations라 부르는 제약 조건으로 인해 $\mathbb{P}^{5}$ 곡면(quadric) 상의 한점과 $\mathbb{P}^{3}$ 공간 상의 직선이 일대일 대응을 이루는 특징이 있다. 이 때, $\mathbb{P}^{3}$ 공간 상의 직선과 대응하는 $\mathbb{P}^{5}$ 곡면을 특별히 Klein quadric이라고 부르며 다음 제약 조건을 만족한다.
\begin{equation}
\begin{aligned}
l_{01}l_{23} + l_{02}l_{31} + l_{03}l_{12} = 0
\end{aligned}
\end{equation}
또는 $l_{31} = -l_{13}$이므로 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
l_{01}l_{23} - l_{02}l_{13} + l_{03}l_{12} = 0
\end{aligned}
\end{equation}
위 식은 (\ref{eq:4}) $\mathbf{m}^{\intercal}\mathbf{d} = 0$ 으로 부터 유도되며 $\det \mathbf{L} = 0$을 통해서도 구할 수 있다.
3.2. Distance to origin
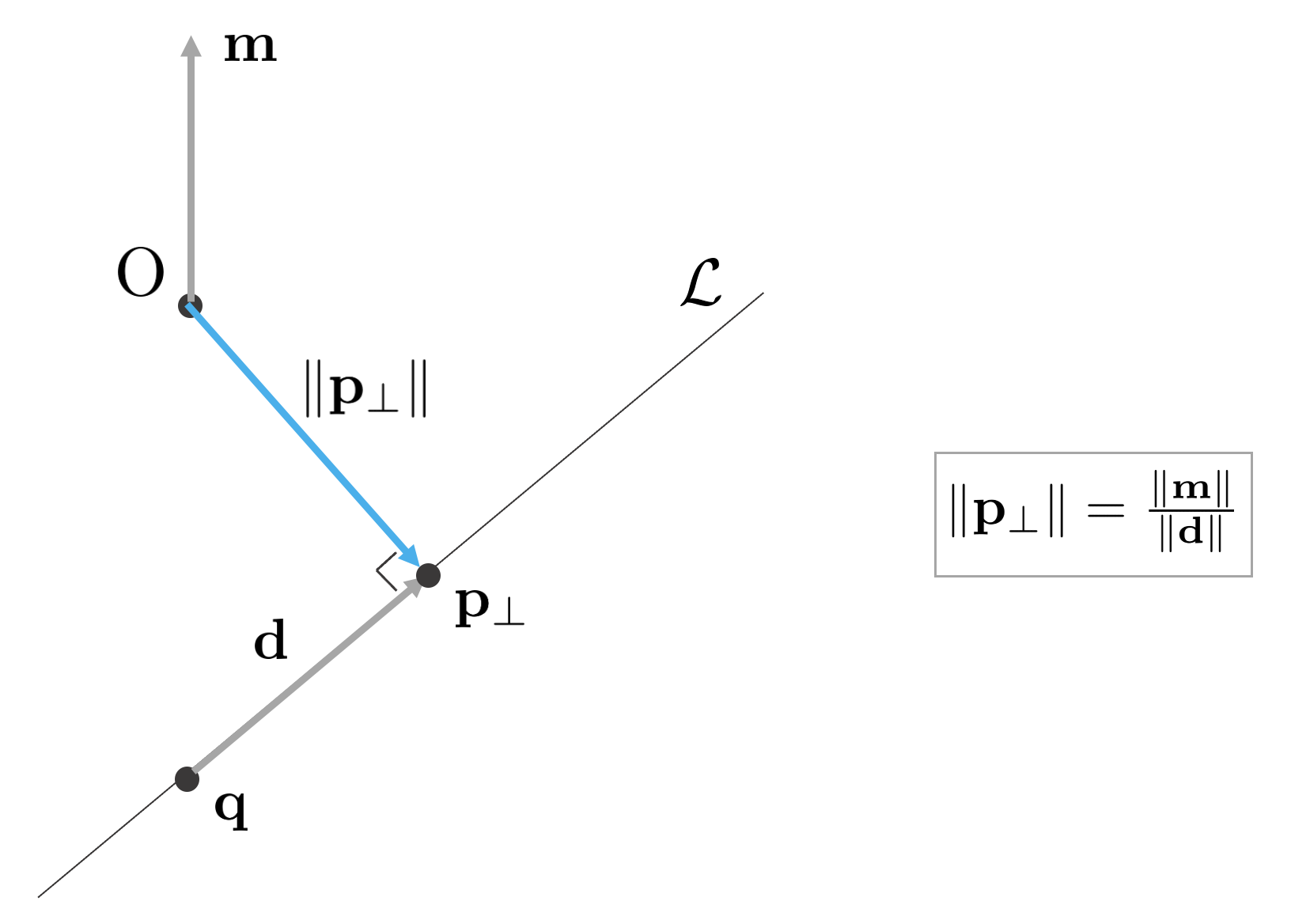
직선이 원점으로부터 떨어진 거리 $\left\| \mathbf{p}_{\perp} \right\|$는 다음과 같이 구할 수 있다. 직선 $\mathcal{L}$ 위의 임의의 점 $\mathbf{q}$가 주어졌고 원점으로부터 직선의 수선의 발이 내려진 점을 $\mathbf{p}_{\perp}$라고 하면 $\mathbf{q}$를 통해 $\mathbf{p}_{\perp}$를 표현할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{q} = \mathbf{p}_{\perp} + k\mathbf{d} \quad (\text{any } \mathbf{q} \text{ on } \mathcal{L})
\end{aligned}
\end{equation}
이에 따라 모멘트 벡터 $\mathbf{m}$은 다음과 같이 전개할 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{m} & = \mathbf{d} \times \mathbf{q} \\
& = \mathbf{d} \times (\mathbf{p}_{\perp} + k\mathbf{d}) \\
& = \mathbf{d} \times \mathbf{p}_{\perp}
\end{aligned}
\end{equation}
모멘트 벡터의 크기 외적의 정의에 따라 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\left\| \mathbf{m} \right\| = \left\| \mathbf{d} \right\|\left\| \mathbf{p}_{\perp} \right\|\sin\frac{\pi}{2} = \left\| \mathbf{d} \right\|\left\| \mathbf{p}_{\perp} \right\|
\end{aligned}
\end{equation}
따라서 원점으로부터 떨어진 직선 $\mathcal{L}$까지의 거리는 다음과 같다.
\begin{equation}
\begin{aligned}
\left\| \mathbf{p}_{\perp} \right\| = \frac{\left\| \mathbf{m} \right\|}{\left\| \mathbf{d} \right\|}
\end{aligned}
\end{equation}
3.3. Up to scale uniqueness
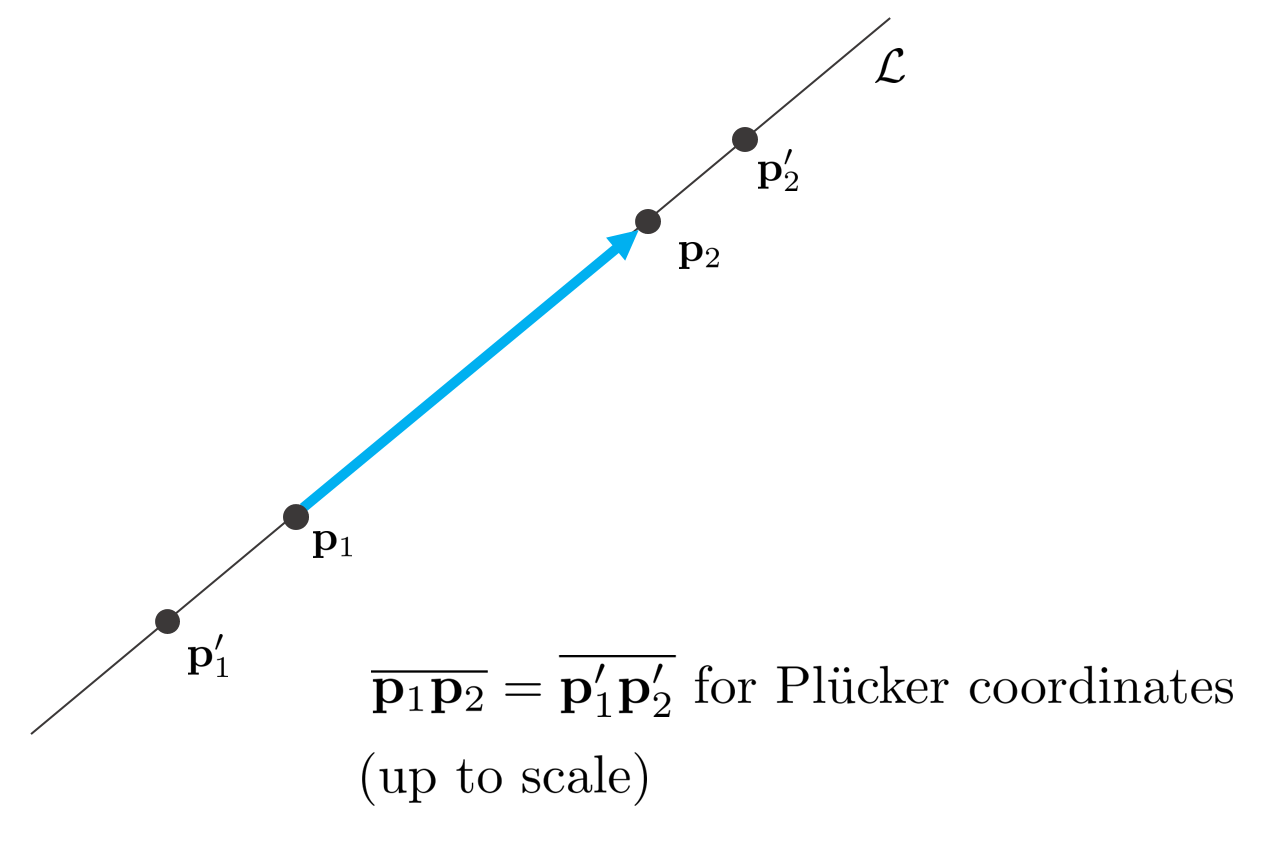
만약 직선 위의 점 $\mathbf{p}_{1}, \mathbf{p}_{2}$가 아닌 직선 위의 임의의 다른 점 $\mathbf{p}^{\prime}_{1}, \mathbf{p}^{\prime}_{2}$가 존재할 때 이는 기존 점들을 통해 표현이 가능하다.
\begin{equation}
\begin{aligned}
& \mathbf{p}_{1}^{\prime} = \lambda \mathbf{p}_{1} + (1-\lambda) \mathbf{p}_{2} \\
& \mathbf{p}_{2}^{\prime} = \mu \mathbf{p}_{1} + (1-\mu) \mathbf{p}_{2}
\end{aligned}
\end{equation}
직선의 방향벡터 $\mathbf{d}^{\prime}$와 모멘트 벡터 $\mathbf{m}$ 또한 기존의 점들을 스케일하여 표현할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{d}^{\prime} = \mathbf{p}_{2}^{\prime} - \mathbf{p}_{1}^{\prime} = (\lambda-\mu)\mathbf{d} \\
& \mathbf{m}^{\prime} = \mathbf{p}_{1}^{\prime} \times \mathbf{p}_{2}^{\prime} = (\lambda-\mu)\mathbf{m} \\
\end{aligned}
\end{equation}
따라서 Plücker Coordinate는 스케일 특성까지만(up to scale) 직선을 유일하게 표현할 수 있다.
3.4. Plücker matrix
$\mathbb{P}^{3}$ 공간에 두 점 $\mathbf{A}, \mathbf{B}$가 존재한다고 하자.
\begin{equation}
\begin{aligned}
& \mathbf{A} = (W_{1}, X_{1}, Y_{1}, Z_{1}) \\
& \mathbf{B} = (W_{2}, X_{2}, Y_{2}, Z_{2})
\end{aligned}
\end{equation}
위 두 점을 사용하여 다음과 같은 Plücker matrix를 정의할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{L} = \mathbf{A}\mathbf{B}^{\intercal} - \mathbf{B}\mathbf{A}^{\intercal} = \begin{bmatrix} 0 & -l_{01} & -l_{02} & -l_{03} \\
l_{01} & 0 & -l_{12} & -l_{13} \\
l_{02} & l_{12} & 0 & -l_{23} \\
l_{03} & l_{13} & l_{23} & 0 \\
\end{bmatrix} \in \mathbb{R}^{4\times4} \\
\end{aligned}
\end{equation}
Plücker matrix는 4x4 반대칭 행렬이며 하삼각(lower-triangle) 행렬의 6개 원소가 곧 Plücker coordinates가 된다.
\begin{equation}
\begin{aligned}
& \mathbf{L} = \mathcal{L}^{\wedge}
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
& \mathcal{L} = (l_{01} : l_{02} : l_{03} : l_{12} : l_{13} : l_{23}) \\
& l_{ij} = A_{i}B_{j} - B_{i}A_{j}
\end{aligned}
\end{equation}
이 때, 주의할 점은 앞서 설명한 Plücker coordinates 순서와 위 수식의 $\mathbf{m}$을 표기하는 순서가 약간 다르다는 것이다.
\begin{equation}
\begin{aligned}
& (1) \ \mathcal{L} = (l_{01} : l_{02} : l_{03} : l_{23} : l_{31} : l_{12})\\
& (2) \ \mathcal{L} = (l_{01} : l_{02} : l_{03} : l_{12} : l_{13} : l_{23})
\end{aligned}
\end{equation}
[3]에서는 $(1)$의 순서로 나와있으나 [1], [2]에서는 $(2)$과 같이 나와있다. 필자의 개인적인 생각으로는 $(1)$의 방법이 $(l_{23} : l_{31} : l_{12}) = (m_{x} : m_{y} : m_{z})$를 만족하므로 맞는 표기로 보이지만 $(2)$ 또한 널리 사용되므로 순서에 유의해서 봐야 한다.
3.3.1. Properties of plücker matrix
Plücker matrix 다음과 같은 성질이 존재한다.
- $\mathbf{L}$ 행렬은 rank 2를 가지며 해당 행렬의 2차원 영공간(null space)는 해당 직선을 지나는 평면 다발(pencil)들에 의해 스팬(span)된다.
- $\mathbf{L}$ 행렬은 4자유도를 가진다. 6개 원소 $l_{ij}$의 homogeneous 특성 상 자유도를 하나 잃고 또한 $\det\mathbf{L} = 0$인 제약조건으로 인해 자유도를 추가적으로 하나 잃어서 총 4자유도를 가진다.
- $\mathbf{L} = \mathbf{A}\mathbf{B}^{\intercal} - \mathbf{B}\mathbf{A}^{\intercal}$는 $\mathbb{P}^{2}$ 공간에서 두 점을 잇는 직선을 $\mathbf{l} = \mathbf{a} \times \mathbf{b}$로 표현하는 방법의 $\mathbb{P}^{3}$ 버전으로 볼 수 있다.
- $\mathbf{a}, \mathbf{b}$: $\mathbf{A,B}$가 이미지 평면에 프로젝션된 점
- $\mathbf{L}$ 행렬은 이를 정의한 두 점 $\mathbf{A}, \mathbf{B}$에 독립적(independent)이다. 만약 직선 위의 점 $\mathbf{C}$가 주어진 경우 $\mathbf{C} = \mathbf{A} + \mu \mathbf{B}$를 통해 나타낼 수 있고 행렬은 다음과 같이 변형된다. \begin{equation}
\begin{aligned}
\hat{\mathbf{L}} & = \mathbf{AC}^{\intercal} - \mathbf{CA}^{\intercal} = \mathbf{A}(\mathbf{A}^{\intercal} + \mu \mathbf{B}^{\intercal}) - (\mathbf{A} + \mu \mathbf{B}) \mathbf{A}^{\intercal} \\
& = \mathbf{A}\mathbf{B}^{\intercal} - \mathbf{B}\mathbf{A}^{\intercal} = \mathbf{L}
\end{aligned}
\end{equation} - $\mathbb{P}^{3}$ 공간 상의 Homography 행렬 $\mathbf{H} \in \mathbb{R}^{4\times 4}$가 3차원 점을 변환할 때 $\mathbf{X}' = \mathbf{HX}$ 같이 적용된다. 이에 상응하는 직선의 Homography 변환은 $\mathbf{L}' = \mathbf{HLH}^{\intercal}$이다.
- 만약 $[W,X,Y,Z]$ 순서가 아닌 $[X,Y,Z,W]$ 순으로 좌표를 나타내면 기존 $\mathcal{L}$은 다음과 같이 변한다. \begin{equation} \begin{aligned} \mathcal{L} & = (\mathbf{d} : \mathbf{m}) \\ &= (l_{01}:l_{02}:l_{03}:l_{23}:l_{31}:l_{12}) \rightarrow (l_{30}:l_{31}:l_{32}:l_{12}:l_{20}:l_{01}) \end{aligned} \label{eq:3} \end{equation}
- 이 때, $\mathbf{L}$ 행렬은 다음과 같이 간단하게 구할 수 있다.\begin{equation} \begin{aligned} & \mathbf{L} = \begin{bmatrix} 0 & -l_{01} & -l_{02} & -l_{03} \\
l_{01} & 0 & -l_{12} & -l_{13} \\
l_{02} & l_{12} & 0 & -l_{23} \\
l_{03} & l_{13} & l_{23} & 0 \\
\end{bmatrix} = \begin{bmatrix} \mathbf{m}^{\wedge} & \mathbf{d} \\ -\mathbf{d}^{\intercal} & 0 \end{bmatrix} \\ \end{aligned} \end{equation} - 주의할 점은 $[W,X,Y,Z]$에서는 위와 같이 간단하게 구하지 못하고 오직 $[X,Y,Z,W]$일 때만 가능한 것으로 보인다.
- 이 때, $\mathbf{L}$ 행렬은 다음과 같이 간단하게 구할 수 있다.\begin{equation} \begin{aligned} & \mathbf{L} = \begin{bmatrix} 0 & -l_{01} & -l_{02} & -l_{03} \\
4. Dual plücker coordinate representation
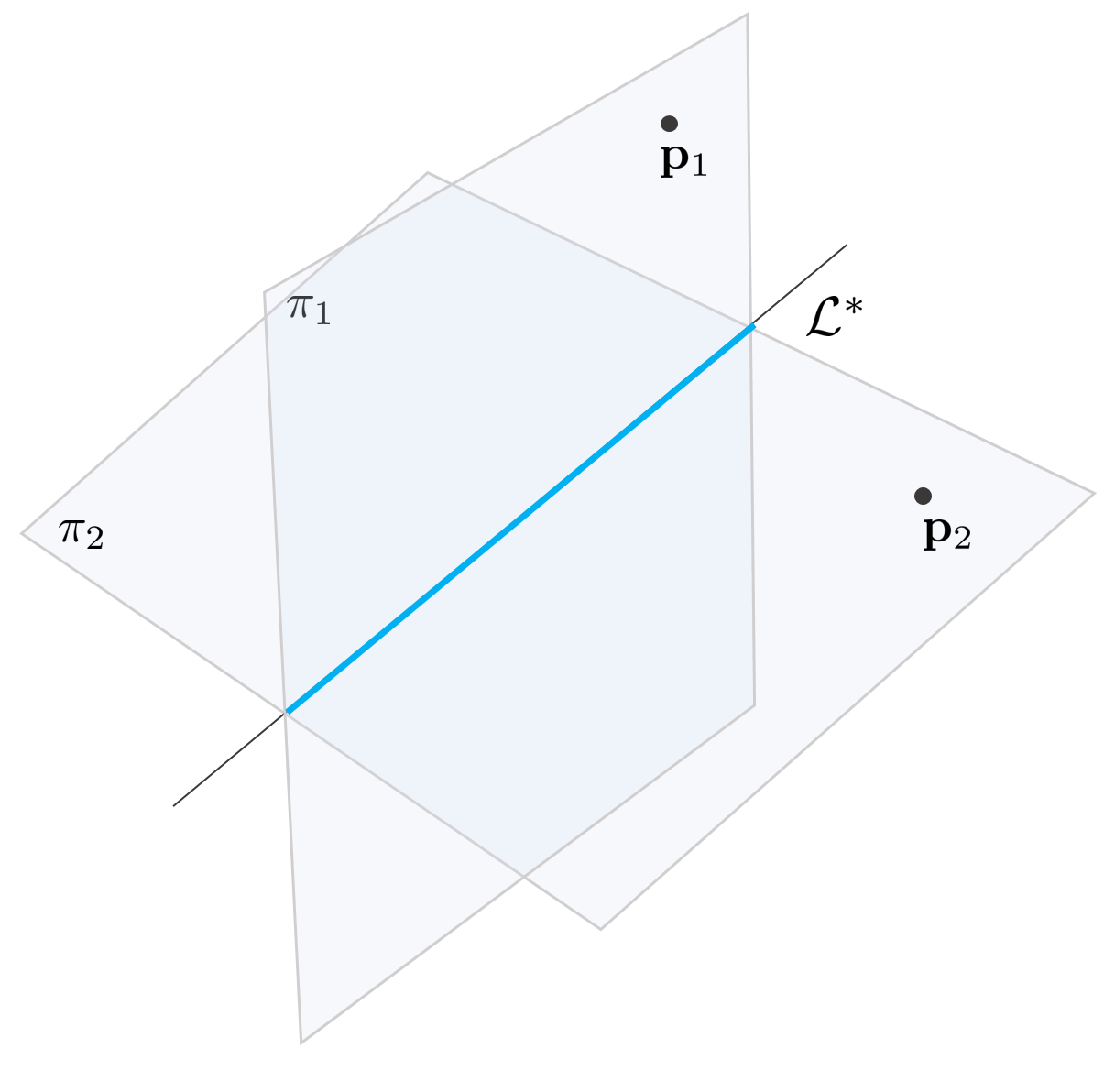
3차원 점을 사용하여 직선을 표현하는 방법과 동일하게 서로 평행하지 않은 두 평면이 교차하는 직선을 사용하여 Plücker Coordinate를 표현할 수 있다. 이렇게 두 평면의 교선으로 직선을 표현하는 방법을 Dual Plücker Coordinate이라고 한다.
3차원 공간 상의 점 $\mathbf{p}_{1}, \mathbf{p}_{2}$이 각각 평면 $\pi_{1}, \pi_{2}$ 위에 있을 때 아래의 공식이 성립한다.
\begin{equation}
\begin{aligned}
& \pi_{1}^{\intercal}\mathbf{p}_{1} = 0, \quad \pi_{2}^{\intercal}\mathbf{p}_{2} = 0 \\
& \begin{bmatrix} a_{w}&a_{x}&a_{y}&a_{z} \end{bmatrix}\begin{bmatrix} W_{1}\\X_{1}\\Y_{1}\\Z_{1} \end{bmatrix} = 0 \\
& \begin{bmatrix} b_{w}&b_{x}&b_{y}&b_{z} \end{bmatrix}\begin{bmatrix} W_{2}\\X_{2}\\Y_{2}\\Z_{2} \end{bmatrix} = 0
\end{aligned}
\end{equation}
위와 같이 평면은 $\pi_{1} = \begin{bmatrix} a_{w}&a_{x}&a_{y}&a_{z} \end{bmatrix}, \pi_{2} = \begin{bmatrix} b_{w}&b_{x}&b_{y}&b_{z} \end{bmatrix}$로 파라미터화 할 수 있다. 서로 평행하지 않은 두 평면을 사용하여 Plücker Coordinates 방법과 동일하게 2x4 행렬 $\mathbf{M}^{*}$를 만들고 2x2 submatrix 연산 $\mathbf{l}^{*}_{ij}$을 정의할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{M}^{*} = \begin{bmatrix} a_{w}&a_{x}&a_{y}&a_{z} \\ b_{w}&b_{x}&b_{y}&b_{z} \end{bmatrix} \\
& l^{*}_{ij} = \begin{vmatrix} a_{x}&a_{y} \\ b_{x}&b_{y} \end{vmatrix} = a_{x}b_{y} - a_{y}b_{x}
\end{aligned}
\end{equation}
Dual Representation으로 표현한 직선 $\mathcal{L}^{*}$은 다음과 같다.
\begin{equation}
\begin{aligned}
\mathcal{L}^{*} = (l^{*}_{23}:l^{*}_{31}:l^{*}_{12}:l^{*}_{01}:l^{*}_{02}:l^{*}_{03})
\end{aligned}
\end{equation}
이는 두 점을 통해 표현한 Plücker Coordinate $\mathcal{L}$의 $l_{ij}$에서 $\{1,2,3,4\}$를 자신이 아닌 다른 값으로 변경한 것과 같다. 예를 들어 $l_{01} \leftrightarrow l^{*}_{23}, l_{12} \leftrightarrow l^{*}_{03}$이 된다.
\begin{equation}
\begin{aligned}
(l_{01}:l_{02}:l_{03}:l_{23}:l_{31}:l_{12}) = (l^{*}_{23}:l^{*}_{31}:l^{*}_{12}:l^{*}_{01}:l^{*}_{02}:l^{*}_{03})
\end{aligned}
\end{equation}
4.1. Dual plücker matrix
$\mathbb{P}^{3}$ 공간에 두 평면 $\mathbf{P}, \mathbf{Q}$가 존재한다고 하자.
\begin{equation}
\begin{aligned}
& \mathbf{P} = [W_{1}, X_{1}, Y_{1}, Z_{1}] \\
& \mathbf{Q} = [W_{2}, X_{2}, Y_{2}, Z_{2}]
\end{aligned}
\end{equation}
Dual plücker matrix $\mathbf{L}^{*}$은 Plücker matrix $\mathbf{L}$와 유사하게 위 두 평면을 사용하여 다음과 같이 정의할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{L}^{*} = \mathbf{P}\mathbf{Q}^{\intercal} - \mathbf{Q}\mathbf{P}^{\intercal} = \begin{bmatrix} 0 & l^{*}_{23} & -l^{*}_{13} & l^{*}_{12} \\
-l^{*}_{23} & 0 & l^{*}_{03} & -l^{*}_{02} \\
l^{*}_{13} & -l^{*}_{03} & 0 & l^{*}_{01} \\
-l^{*}_{12} & l^{*}_{02} & -l^{*}_{01} & 0 \\
\end{bmatrix} \in \mathbb{R}^{4\times4} \\
\end{aligned}
\end{equation}
4.1.1. Properties of dual plücker matrix
Dual plücker matrix의 성질은 다음과 같다.
- $\mathbb{P}^{3}$ 공간 상의 Homography 행렬 $\mathbf{H} \in \mathbb{R}^{4\times 4}$가 3차원 점을 변환할 때 $\mathbf{X}' = \mathbf{HX}$ 같이 적용된다. 이에 상응하는 dual 직선의 Homography 변환은 $\mathbf{L}^{*'} = \mathbf{H}^{-\intercal}\mathbf{L}\mathbf{H}^{-1}$이다.
- 직선 $\mathcal{L}$과 평면 $\pi$가 주어졌을 때, 둘이 만나는 교점은 $\mathbf{X} = \mathbf{L}\pi$를 통해 구할 수 있다. 그리고 직선 $\mathcal{L}$과 점 $\mathbf{X}$가 주어졌을 때 둘을 포함하는 평면은 $\pi = \mathbf{L}^{*}\mathbf{X}$를 통해 구할 수 있다. 자세한 내용은 해당 섹션의 내용을 참조하면 된다.
- 이 때, 평면 $\pi$ 위에 직선 $\mathcal{L}$이 존재하거나 직선 $\mathcal{L}$ 위에 점 $\mathbf{X}$이 존재하면 각각 $\mathbf{L}\pi = 0$, $\mathbf{L}^{*}\mathbf{X} = 0$이 된다. 해당 식을 이어서 표현하면 다음과 같다. \begin{equation}\begin{aligned} \mathbf{X} & = \mathbf{L}\pi = 0 \\ \mathbf{L}^{*}\mathbf{X} & = \mathbf{L}^{*}\mathbf{L}\pi = 0 \\ \therefore \mathbf{L}^{*}\mathbf{L} & = 0 \in \mathbb{R}^{4\times4} \end{aligned}\end{equation}
- 위 식을 풀어서 표현하면 다음과 같다. \begin{equation}\begin{aligned} & \begin{bmatrix} 0 & l^{*}_{23} & -l^{*}_{13} & l^{*}_{12} \\
-l^{*}_{23} & 0 & l^{*}_{03} & -l^{*}_{02} \\
l^{*}_{13} & -l^{*}_{03} & 0 & l^{*}_{01} \\
-l^{*}_{12} & l^{*}_{02} & -l^{*}_{01} & 0 \\
\end{bmatrix} \begin{bmatrix} 0 & -l_{01} & -l_{02} & -l_{03} \\
l_{01} & 0 & -l_{12} & -l_{13} \\
l_{02} & l_{12} & 0 & -l_{23} \\
l_{03} & l_{13} & l_{23} & 0 \\
\end{bmatrix} = 0 \\ & [l_{01}l_{23} -l_{02}l_{13} + l_{03}l_{12}] \begin{bmatrix} 1&&& \\ &1&& \\ &&1& \\ &&&1 \end{bmatrix} = 0 \end{aligned}\end{equation} - 위 식은 앞서 설명한 Graßmann–Plücker relation 제약조건으로 인해 0을 만족한다.
- 만약 $[W,X,Y,Z]$ 순서가 아닌 $[X,Y,Z,W]$ 순으로 좌표를 나타내면 기존 $\mathcal{L}^{*}$은 다음과 같이 변한다. \begin{equation} \begin{aligned} \mathcal{L} & = (\mathbf{d} : \mathbf{m}) \\ & = (l_{01}:l_{02}:l_{03}:l_{23}:l_{31}:l_{12}) \rightarrow (l_{30}:l_{31}:l_{32}:l_{12}:l_{20}:l_{01}) \\ \mathcal{L}^{*} & = (-\mathbf{m} : -\mathbf{d}) \\ & = (l^{*}_{23}:l^{*}_{31}:l^{*}_{12}:l^{*}_{01}:l^{*}_{02}:l^{*}_{03}) \rightarrow (l^{*}_{21} : l^{*}_{02} : l^{*}_{10} : l^{*}_{03} : l^{*}_{13} : l^{*}_{23}) \end{aligned} \end{equation}
- 이 때, $\mathbf{L}^{*}$ 행렬은 다음과 같이 간단하게 구할 수 있다.\begin{equation} \begin{aligned} & \mathbf{L}^{*} = \begin{bmatrix} 0 & l^{*}_{23} & -l^{*}_{13} & l^{*}_{12} \\
-l^{*}_{23} & 0 & l^{*}_{03} & -l^{*}_{02} \\
l^{*}_{13} & -l^{*}_{03} & 0 & l^{*}_{01} \\
-l^{*}_{12} & l^{*}_{02} & -l^{*}_{01} & 0 \\
\end{bmatrix}= \begin{bmatrix} -\mathbf{d}^{\wedge} & \mathbf{m} \\ -\mathbf{m}^{\intercal} & 0 \end{bmatrix} \\ \end{aligned} \end{equation} - 주의할 점은 $[W,X,Y,Z]$에서는 위와 같이 간단하게 구하지 못하고 오직 $[X,Y,Z,W]$일 때만 가능한 것으로 보인다.
- 이 때, $\mathbf{L}^{*}$ 행렬은 다음과 같이 간단하게 구할 수 있다.\begin{equation} \begin{aligned} & \mathbf{L}^{*} = \begin{bmatrix} 0 & l^{*}_{23} & -l^{*}_{13} & l^{*}_{12} \\
5. Uses
5.1. Line-line crossing
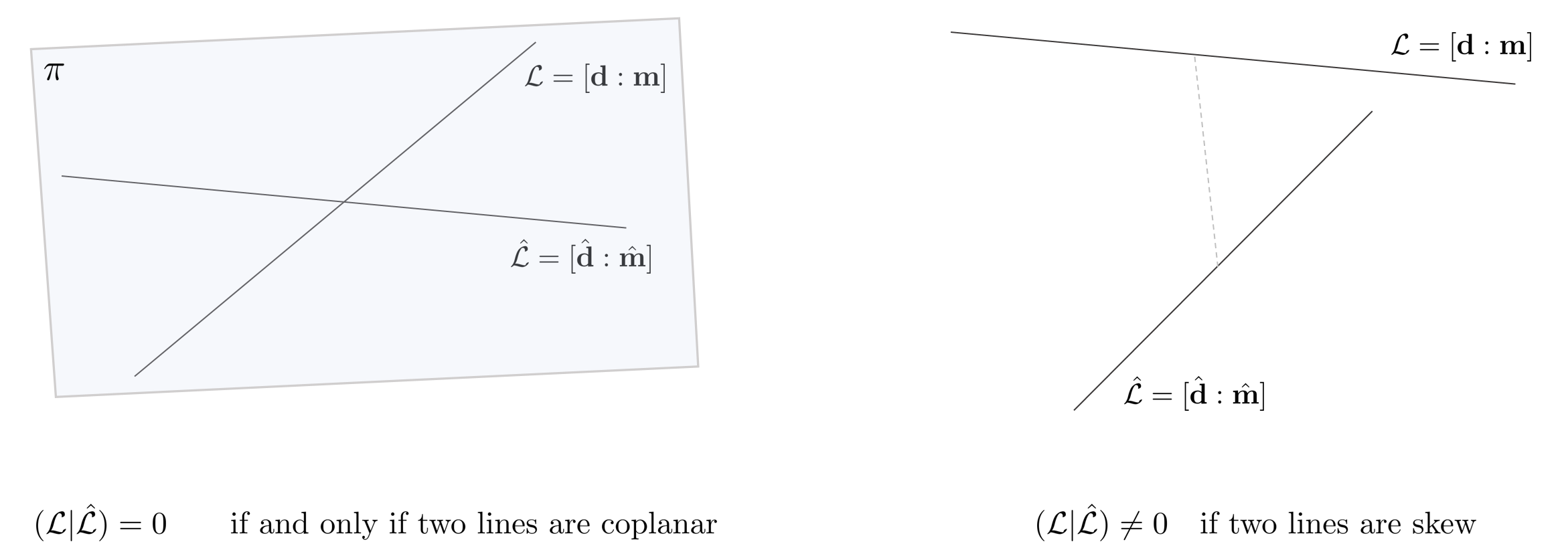
$\mathbb{P}^{3}$ 공간 상의 동일한 평면 위에 존재하는(coplanar) 두 직선 $\mathcal{L}, \hat{\mathcal{L}}$가 주어졌다고 가정하자. 직선 $\mathcal{L}$이 두 점 $\mathbf{A}, \mathbf{B}$에 의해 결정되고 $\hat{\mathcal{L}}$이 두 점 $\hat{\mathbf{A}}, \hat{\mathbf{B}}$에 의해 결정된다고 했을 때 두 직선의 행렬식은 다음과 같이 쓸 수 있다.
\begin{equation}
\begin{aligned}
\det[\mathbf{A}, \mathbf{B}, \hat{\mathbf{A}}, \hat{\mathbf{B}}] & = l_{12}\hat{l}_{34} + \hat{l}_{12} l_{34} + l_{13}\hat{l}_{42} + \hat{l}_{13} l_{42} + l_{14}\hat{l}_{23} + \hat{l}_{14} l_{23} \\
& = (\mathcal{L} | \hat{\mathcal{L}})
\end{aligned} \end{equation}
해당 섹션에서 설명한 것처럼 $\mathcal{L}$과 $\hat{\mathcal{L}}$은 해당 직선을 결정지은 점들로부터 독립적이므로 $(\mathcal{L} | \hat{\mathcal{L}})$은 $\mathbf{A}, \mathbf{B}, \hat{\mathbf{A}}, \hat{\mathbf{B}}$ 뿐만 아니라 해당 직선 위의 모든 점들에 대해 만족한다. 두 직선이 동일한 평면 위에 존재하려면 $\det[\mathbf{A}, \mathbf{B}, \hat{\mathbf{A}}, \hat{\mathbf{B}}] = 0$을 만족해야 한다.
\begin{equation}
\begin{aligned}
(\mathcal{L} | \hat{\mathcal{L}}) = 0 \quad \quad \text{if and only if two lines are coplanar}
\end{aligned} \end{equation}
이는 다음과 같은 유용한 성질들을 도출한다.
- 임의의 6차원 벡터 $\mathcal{L}$가 $(\mathcal{L} | \mathcal{L}) = 0$을 만족하면 이는 $\mathbb{P}^{3}$ 공간 상의 한 직선을 표현할 수 있다. 이는 앞서 설명한 Klein quadric 제약조건과 동일하다.
- 두 직선 $\mathcal{L}, \hat{\mathcal{L}}$은 두 평면들로부터 결정될 수 있다. $\mathcal{L}$가 두 평면 $\mathbf{P}, \mathbf{Q}$로부터 결정되고 $\hat{\mathcal{L}}$가 두 평면 $\hat{\mathbf{P}}, \hat{\mathbf{Q}}$로부터 결정된다고 하면 다음 제약 조건을 만족한다. \begin{equation}
\begin{aligned}
(\mathcal{L} | \hat{\mathcal{L}}) = \det[\mathbf{P}, \mathbf{Q}, \hat{\mathbf{P}}, \hat{\mathbf{Q}}]
\end{aligned} \end{equation} 앞서 설명한 내용과 동일하게 두 직선은 $(\mathcal{L} | \mathcal{L}) = 0$일 때 서로 교차(intersect)한다. - 직선 $\mathcal{L}$가 두 평면 $\mathbf{P}, \mathbf{Q}$로부터 결정되고 $\hat{\mathcal{L}}$가 두 점 $\mathbf{A}, \mathbf{B}$로부터 결정된다고 하면 다음 제약 조건을 만족한다. \begin{equation}
\begin{aligned}
(\mathcal{L} | \hat{\mathcal{L}}) = (\mathbf{P}^{\intercal}\mathbf{A})(\mathbf{Q}^{\intercal}\mathbf{B}) - (\mathbf{Q}^{\intercal}\mathbf{A})(\mathbf{P}^{\intercal}\mathbf{B})
\end{aligned} \label{eq:1} \end{equation}
5.2. Line-line join (Plane)
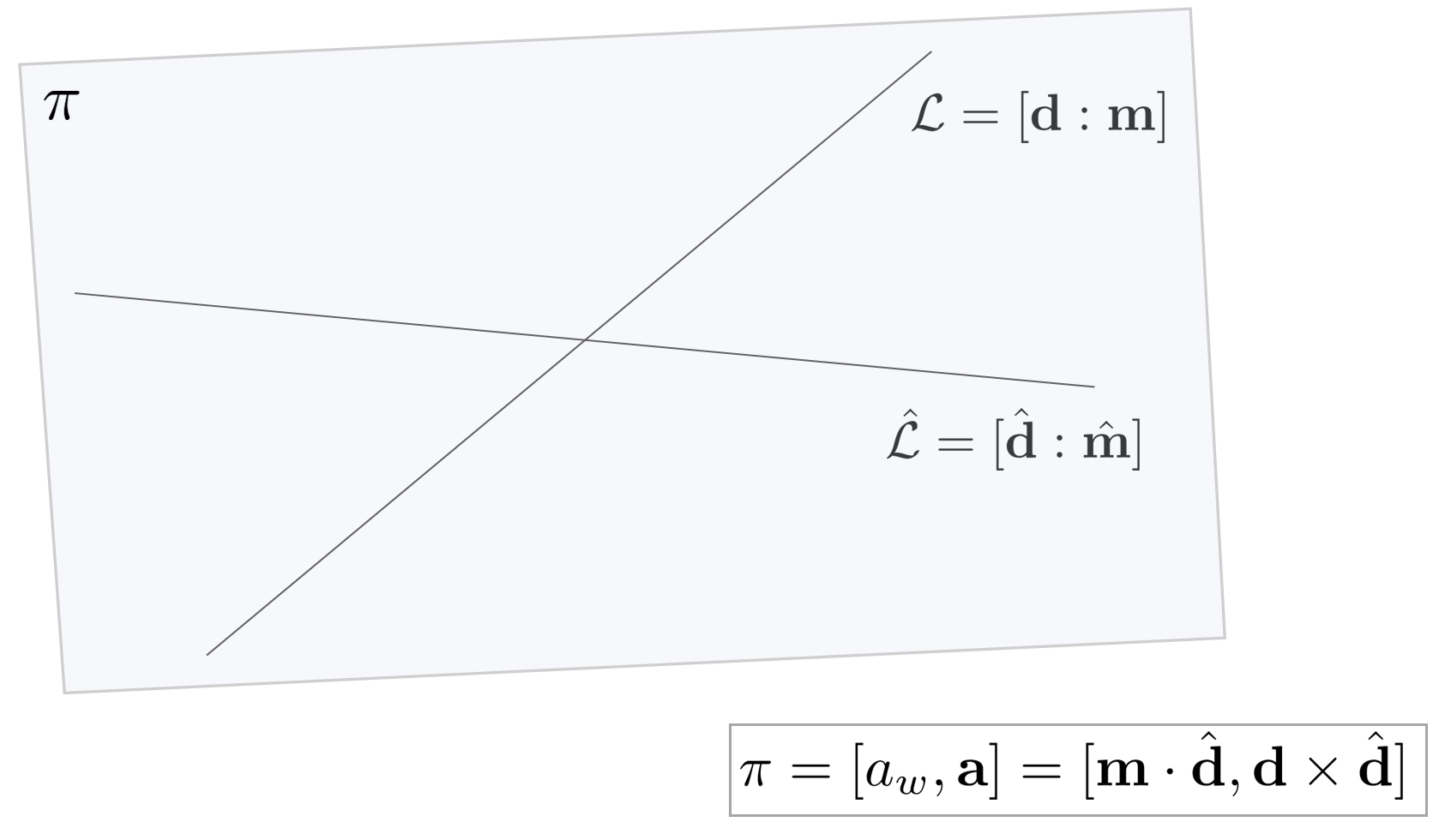
$\mathbb{P}^{3}$ 공간 상의 두 직선 $\mathcal{L}, \hat{\mathcal{L}}$이 동일한 평면 $\pi$위에 존재하고(coplanar) 서로 평행하지 않은 경우 두 직선을 통해 평면 $\pi$를 구할 수 있다.
\begin{equation} \begin{aligned}
& \mathcal{L} = [\mathbf{d} : \mathbf{m}] \\
& \hat{\mathcal{L}} = [\hat{\mathbf{d}} : \hat{\mathbf{m}}] \\
& \pi = [a_w, a_x, a_y, a_z] = [a_{w}, \mathbf{a}]
\end{aligned} \end{equation}
다음 공식을 통해 평면 $\pi$를 구할 수 있다.
\begin{equation} \begin{aligned}
\pi = [a_{w}, \mathbf{a}] = [\mathbf{m} \cdot \hat{\mathbf{d}}, \mathbf{d} \times \hat{\mathbf{d}}]
\end{aligned} \end{equation}
5.3. Line-line meet (Point)
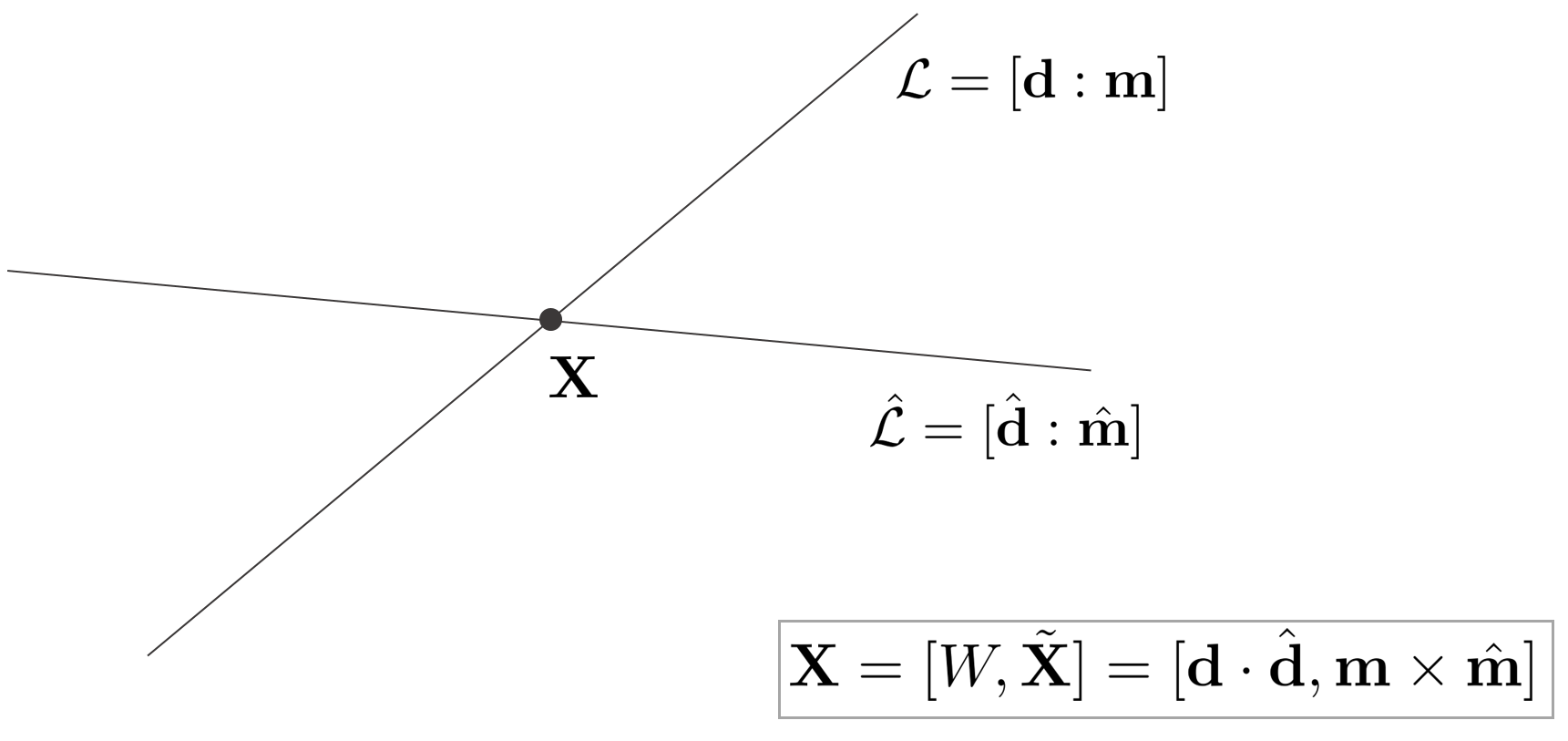
$\mathbb{P}^{3}$ 공간 상의 두 직선 $\mathcal{L}, \hat{\mathcal{L}}$이 동일한 평면 위에 존재하고(coplanar) 서로 평행하지 않은 경우 두 직선은 한 점 $\mathbf{X}$에서 만난다.
\begin{equation} \begin{aligned}
& \mathcal{L} = [\mathbf{d} : \mathbf{m}], \quad \\
& \hat{\mathcal{L}} = [\hat{\mathbf{d}} : \hat{\mathbf{m}}] \\
& \mathbf{X} = [W,X,Y,Z] = [W, \tilde{\mathbf{X}}]
\end{aligned} \end{equation}
다음 공식을 통해 3차원 점 $\mathbf{X}$을 구할 수 있다.
\begin{equation} \begin{aligned}
\mathbf{X} = [W, \tilde{\mathbf{X}}] = [\mathbf{d} \cdot \hat{\mathbf{d}}, \mathbf{m} \times \hat{\mathbf{m}}]
\end{aligned} \end{equation}
5.4. Plane-line meet (Point)
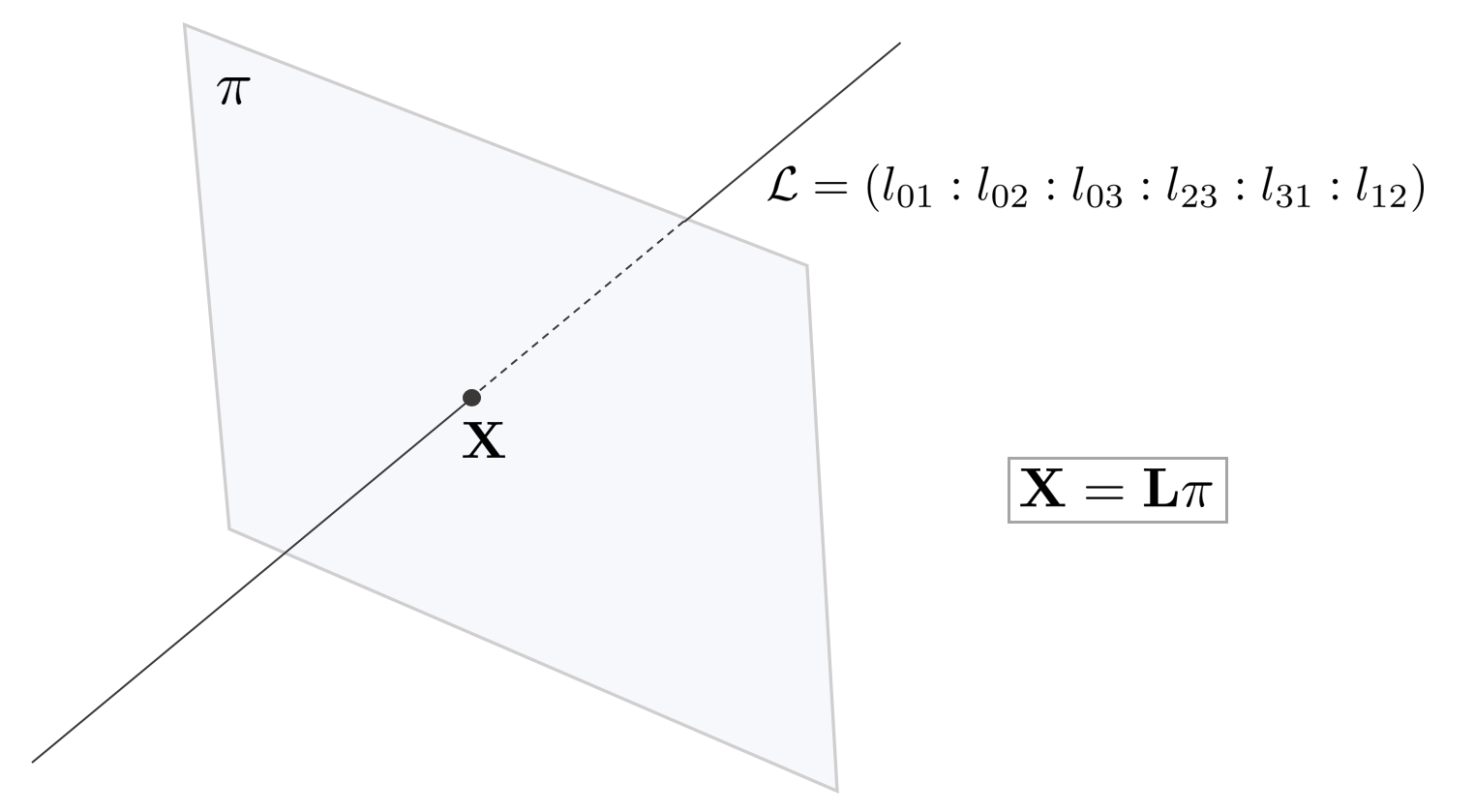
3차원 공간 상의 한 직선 $\mathcal{L}$과 평면 $\pi$의 교점으로 생성되는 한 점 $\mathbf{X}$는 다음과 같이 정의된다. \begin{equation}
\begin{aligned}
\mathbf{X} = \mathbf{L}\pi
\end{aligned}
\end{equation}
만약 직선 $\mathcal{L}$이 평면 $\pi$ 위에 존재하면 $\mathbf{L}\pi = 0$이 된다.
조금 더 자세하게 벡터로 풀어서 설명하면 다음과 같다.
\begin{equation} \begin{aligned}
& \mathcal{L} = [\mathbf{d} : \mathbf{m}], \quad \\
& \pi = [a_w, a_x, a_y, a_z] = [a_{w}, \mathbf{a}] \\
& \mathbf{X} = [W,X,Y,Z] = [W, \tilde{\mathbf{X}}]
\end{aligned} \end{equation}
따라서 직선과 평면의 교점으로 생성되는 한 점 $\mathbf{X}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{X} = [W, \tilde{\mathbf{X}}] = [\mathbf{a} \cdot \mathbf{d}, \mathbf{a} \times \mathbf{m} - a_{w}\mathbf{d}]
\end{aligned}
\end{equation}
5.5. Point-line join (Plane)
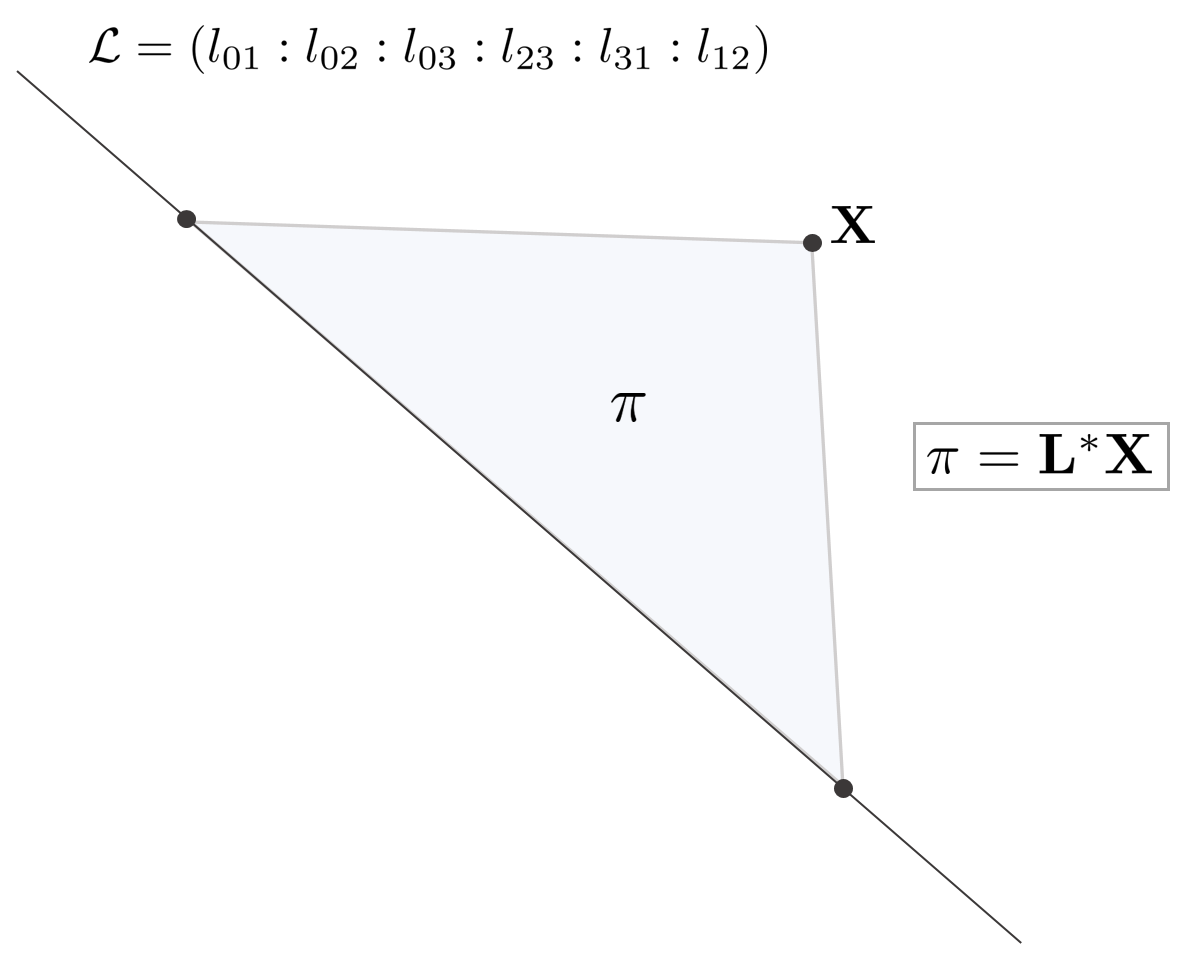
3차원 공간 상의 한 점 $\mathbf{X}$와 직선 $\mathcal{L}$로 인해 생성되는 평면 $\pi$는 다음과 같이 나타낼 수 있다. \begin{equation}
\begin{aligned}
\pi = \mathbf{L}^{*}\mathbf{X}
\end{aligned}
\end{equation}
만약 $\mathbf{X}$가 직선 $\mathcal{L}$ 위에 존재하면 $\mathbf{L}^{*}\mathbf{X} = 0$이 된다. Dual plücker matrix $\mathbf{L}^{*}$에 대한 자세한 설명은 해당 섹션에서 설명한다.
조금 더 자세하게 벡터로 풀어서 설명하면 다음과 같다.
\begin{equation} \begin{aligned}
& \mathcal{L} = [\mathbf{d} : \mathbf{m}], \quad \\
& \mathbf{X} = [W,X,Y,Z] = [W, \tilde{\mathbf{X}}] \\ & \pi = [a_w, a_x, a_y, a_z] = [a_{w}, \mathbf{a}]
\end{aligned} \end{equation}
따라서 직선과 한 점으로 인해 생성되는 평면 $\pi$는 다음과 같다.
\begin{equation}
\begin{aligned}
\pi = [a_{w}, \mathbf{a}] = [\tilde{\mathbf{X}}\cdot \mathbf{m}, \tilde{\mathbf{X}} \times \mathbf{d} - W\mathbf{m}]
\end{aligned}
\end{equation}
5.6. Line projection to the image plane
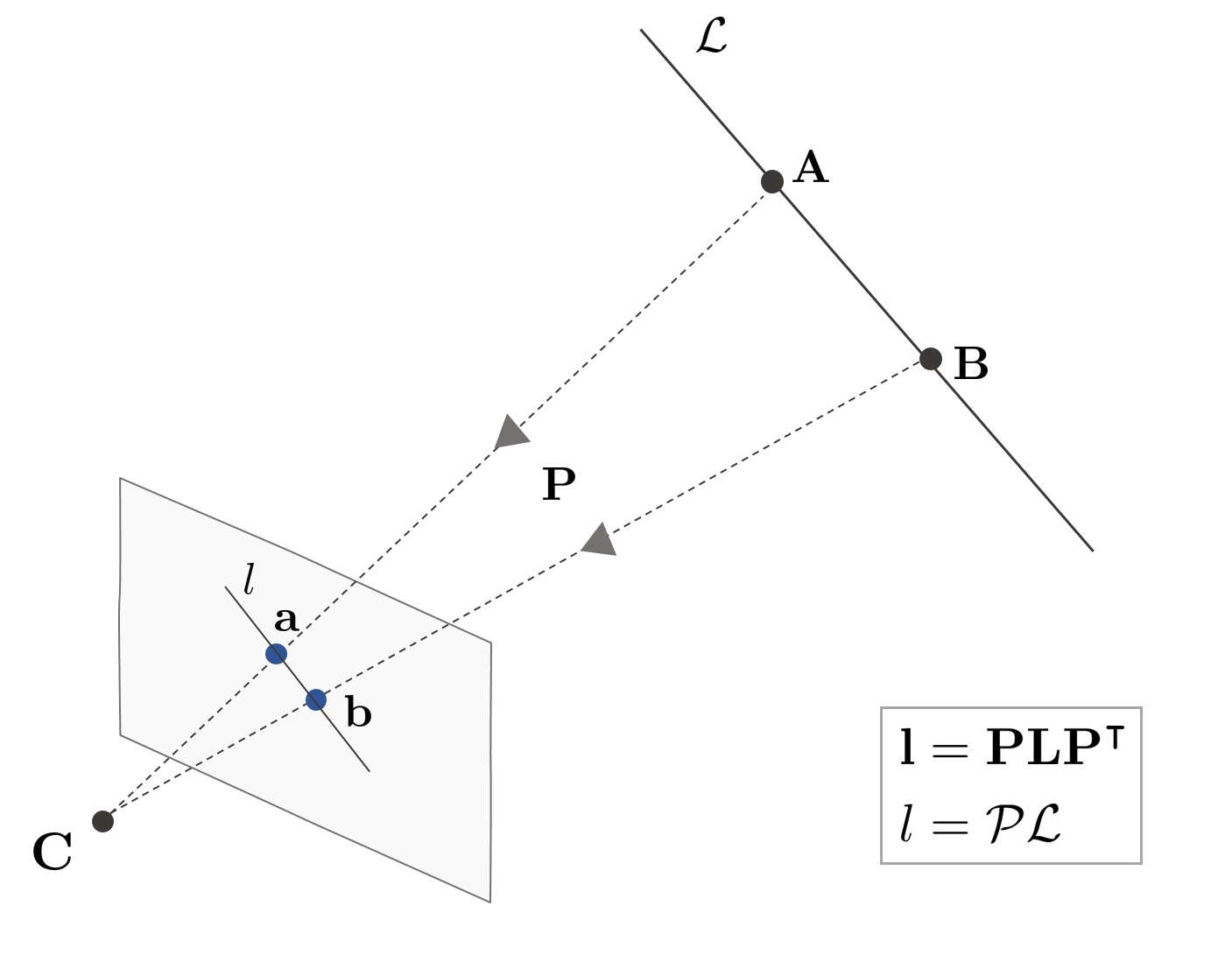
3차원 공간 상의 점 $\mathbf{A}, \mathbf{B}$와 두 점을 잇는 직선 $\mathcal{L}$이 주어졌다고 하자. 카메라 프로젝션 행렬 $\mathbf{P}$가 있을 때 직선 $\mathcal{L}$을 이미지 평면에 프로젝션한 직선의 이미지(image of the line) $l$의 plücker matrix $\mathbf{l}$은 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
l^{\wedge} = \mathbf{l} = \mathbf{P}\mathbf{L}\mathbf{P}^{\intercal} \in \mathbb{R}^{3\times3}
\end{aligned} \label{eq:5}
\end{equation}
- $\mathcal{L}$: 3차원 공간 상의 직선
- $\mathbf{L} = \mathcal{L}^{\wedge}$: 3차원 공간 상의 직선의 plücker matrix (반대칭 행렬)
- $l$: 이미지 평면에 프로젝션된 직선
- $\mathbf{l} = l^{\wedge}$: 프로젝션된 직선의 plücker matrix (반대칭 행렬)
5.6.1. Line projection matrix
직선의 프로젝션 행렬 $\mathcal{P}$를 사용하면 위처럼 3차원 공간 상의 직선 $\mathcal{L}$을 plücker matrix의 형태 $\mathbf{L}$로 변환하여 $\mathbf{l}$을 구하지 않고 바로 $l$을 구할 수 있다. 임의의 카메라 프로젝션 행렬 $\mathbf{P} = [\mathbf{N} | \mathbf{n}] \in \mathbb{R}^{3\times 4}$와 같이 주어졌을 때 $\mathcal{P}$는 다음과 같이 정의할 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{P} = [\det(\mathbf{N}) \mathbf{N}^{-\intercal} | \mathbf{n}^{\wedge} \mathbf{N} ] \in \mathbb{R}^{3\times 6}
\end{aligned} \label{eq:6}
\end{equation}
만약 $\mathbf{P} = [ \mathbf{R} | \mathbf{t} ]$인 경우 위 식은 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{P} = [\mathbf{R} \ | \ \mathbf{t}^{\wedge} \mathbf{R} ] \in \mathbb{R}^{3\times 6}
\end{aligned}
\end{equation}
이는 다음과 같은 식을 통해 유도할 수 있다. 3차원 공간 상의 두 점 $\mathbf{A}=[\tilde{\mathbf{A}} | a], \mathbf{B} = [\tilde{\mathbf{B}} | b] \in \mathbb{P}^{3}$가 주어졌을 때 두 점을 프로젝션한 이미지 평면 상의 두 점 $\mathbf{a}, \mathbf{b} \in \mathbb{P}^{2}$이 있다고 하자. 이를 통해 직선 $l$을 구할 수 있다.
\begin{equation}
\begin{aligned}
l & = \mathbf{a} \times \mathbf{b} \\
& = \mathbf{PA} \times \mathbf{PB} \\
& = (\mathbf{N}\tilde{\mathbf{A}} + a\mathbf{n}) \times (\mathbf{N}\tilde{\mathbf{B}} + b\mathbf{n}) \\
& = (\mathbf{N}\tilde{\mathbf{A}}) \times (\mathbf{N}\tilde{\mathbf{B}}) + a\mathbf{n} \times (\mathbf{N}\tilde{\mathbf{B}}) - b\mathbf{n} \times (\mathbf{N}\tilde{\mathbf{A}}) \\
& = \det(\mathbf{N}) \mathbf{N}^{-\intercal} (\tilde{\mathbf{A}} \times \tilde{\mathbf{B}}) + \mathbf{n}^{\wedge} \mathbf{N}(a \tilde{\mathbf{B}} - b\tilde{\mathbf{A}}) \\
& = [\det(\mathbf{N}) \mathbf{N}^{-\intercal} | \mathbf{n}^{\wedge} \mathbf{N} ] \cdot [ \mathbf{m}^{\intercal} | \mathbf{d}^{\intercal} ]^{\intercal} \\
& = \mathcal{PL}
\end{aligned} \label{eq:7}
\end{equation}
- $\mathbf{m} = \tilde{\mathbf{A}} \times \tilde{\mathbf{B}}$
- $\mathbf{d} = a \tilde{\mathbf{B}} - b\tilde{\mathbf{A}}$
다섯번 째 라인의 유도는 해당 링크에서 확인할 수 있다.
이와 다른 방식으로 $\mathcal{P}$를 구할 수도 있다. 우선 다른 방식으로 표현한 $\mathcal{P}$는 다음과 같다.
\begin{equation}
\begin{aligned}
\mathcal{P} = \begin{bmatrix} \mathbf{p}_{2,row} \wedge \mathbf{p}_{3,row} \\ \mathbf{p}_{3,row} \wedge \mathbf{p}_{1,row} \\ \mathbf{p}_{1,row} \wedge \mathbf{p}_{2,row} \end{bmatrix} \in \mathbb{R}^{3\times 6}
\end{aligned}
\end{equation}
- $\mathbf{P} = \begin{bmatrix} \mathbf{p}_{1,row}^{\intercal} \\ \mathbf{p}_{2,row}^{\intercal} \\ \mathbf{p}_{3,row}^{\intercal} \end{bmatrix} \in \mathbb{R}^{3\times 4}$: 카메라 프로젝션 행렬
- $\mathbf{p}_{i,row} \in \mathbb{R}^{1\times4}$: $\mathbf{P}$의 $i$번째 행벡터. $i=1,2,3$을 기준으로 각각 $X,Y,Z$ 축과 평행한 평면을 의미한다.
- $\mathbf{p}_{i,row} \wedge \mathbf{p}_{j,row} \in \mathbb{R}^{1\times6}$: 두 평면 $\mathbf{p}_{i,row}$와 $\mathbf{p}_{j,row}$의 교차선으로 인해 생성되는 직선의 plücker coordinates
이를 통해 $l$를 구하면 다음과 같다.
\begin{equation}
\begin{aligned}
l = \mathcal{P}\mathcal{L} = \begin{bmatrix} ( \mathbf{p}_{2,row} \wedge \mathbf{p}_{3,row} | \mathcal{L} ) \\ ( \mathbf{p}_{3,row} \wedge \mathbf{p}_{1,row} | \mathcal{L} ) \\ ( \mathbf{p}_{1,row} \wedge \mathbf{p}_{2,row} | \mathcal{L} ) \end{bmatrix}
\end{aligned}
\end{equation}
3차원 공간 상의 두 점 $\mathbf{A}, \mathbf{B}$를 프로젝션한 $\mathbf{a}, \mathbf{b}$는 각각 $\mathbf{a} = \mathbf{PA}, \mathbf{b} = \mathbf{PB}$와 같이 나타낼 수 있고 직선의 이미지 $l = \mathbf{a} \times \mathbf{b} = (\mathbf{PA} \times \mathbf{PB})$와 같이 나타낼 수 있으므로 (\ref{eq:1})에 따라 아래와 같이 전개할 수 있다.
\begin{equation}
\begin{aligned}
l & = \mathbf{PA} \times \mathbf{PB} \\
& = \bigg( \begin{bmatrix} \mathbf{p}_{1,row} \\ \mathbf{p}_{2,row} \\ \mathbf{p}_{3,row} \end{bmatrix} \mathbf{A} \bigg) \times \bigg( \begin{bmatrix} \mathbf{p}_{1,row} \\ \mathbf{p}_{2,row} \\ \mathbf{p}_{3,row} \end{bmatrix} \mathbf{B} \bigg) \\
& = \begin{bmatrix} \mathbf{p}_{1,row}\mathbf{A} \\ \mathbf{p}_{2,row}\mathbf{A} \\ \mathbf{p}_{3,row}\mathbf{A} \end{bmatrix} \times \begin{bmatrix} \mathbf{p}_{1,row}\mathbf{B} \\ \mathbf{p}_{2,row}\mathbf{B} \\ \mathbf{p}_{3,row}\mathbf{B} \end{bmatrix} \\
& = \begin{bmatrix} 0 & -\mathbf{p}_{3,row}\mathbf{A} & \mathbf{p}_{2,row}\mathbf{A} \\ \mathbf{p}_{3,row}\mathbf{A} & 0 & -\mathbf{p}_{1,row}\mathbf{A} \\ -\mathbf{p}_{2,row}\mathbf{A} & \mathbf{p}_{1,row}\mathbf{A} & 0 \end{bmatrix} \begin{bmatrix} \mathbf{p}_{1,row}\mathbf{B} \\ \mathbf{p}_{2,row}\mathbf{B} \\ \mathbf{p}_{3,row}\mathbf{B} \end{bmatrix} \\
& = \begin{bmatrix} (\mathbf{p}_{2,row}^{\intercal}\mathbf{A})(\mathbf{p}_{3,row}^{\intercal}\mathbf{B}) - (\mathbf{p}_{2,row}^{\intercal}\mathbf{B}) (\mathbf{p}_{3,row}^{\intercal}\mathbf{A}) \\ (\mathbf{p}_{3,row}^{\intercal}\mathbf{A})(\mathbf{p}_{1,row}^{\intercal}\mathbf{B}) - (\mathbf{p}_{3,row}^{\intercal}\mathbf{B}) (\mathbf{p}_{1,row}^{\intercal}\mathbf{A}) \\ (\mathbf{p}_{1,row}^{\intercal}\mathbf{A})(\mathbf{p}_{2,row}^{\intercal}\mathbf{B}) - (\mathbf{p}_{1,row}^{\intercal}\mathbf{B}) (\mathbf{p}_{2,row}^{\intercal}\mathbf{A}) \end{bmatrix} && \\
& = \begin{bmatrix} (\mathbf{p}_{2,row} \wedge \mathbf{p}_{3,row} | \mathcal{L}) \\ (\mathbf{p}_{3,row} \wedge \mathbf{p}_{1,row} | \mathcal{L}) \\ (\mathbf{p}_{1,row} \wedge \mathbf{p}_{2,row} | \mathcal{L}) \end{bmatrix} && \cdots \text{ by } (\ref{eq:1})
\end{aligned}
\end{equation}
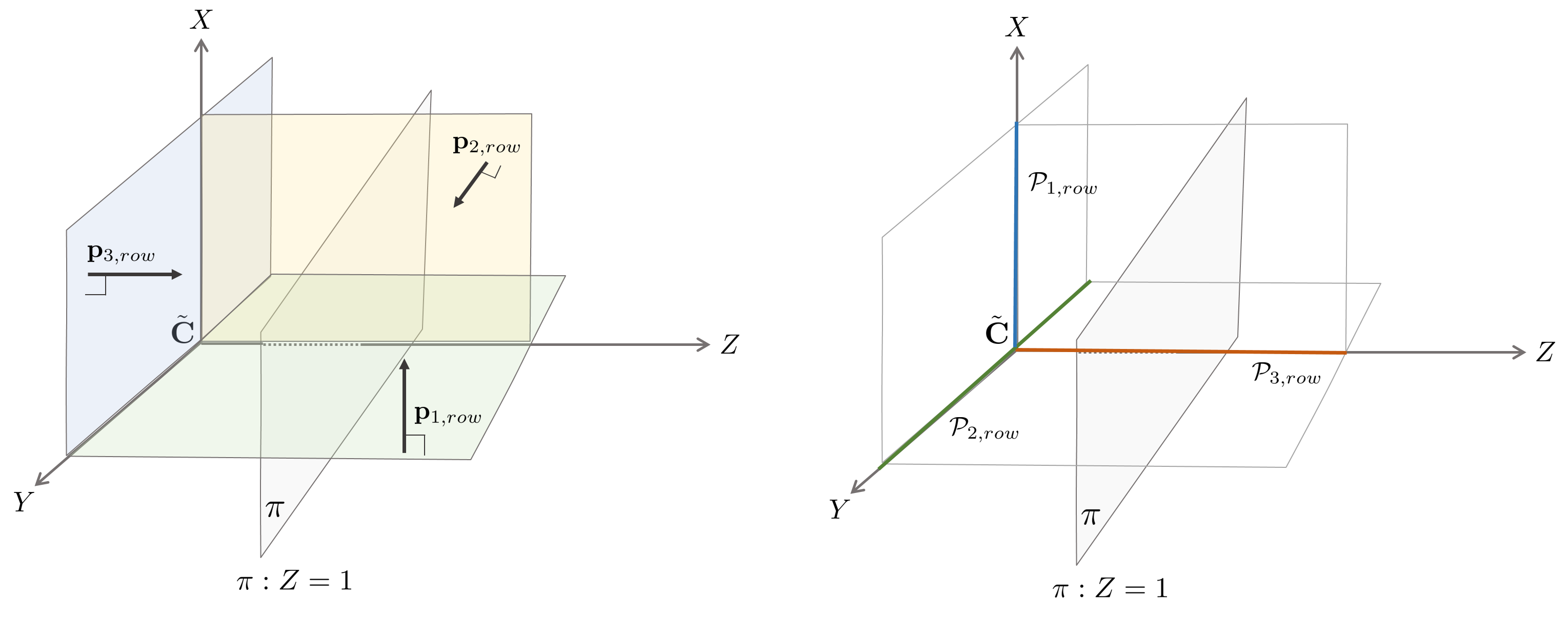
$\mathcal{P}$ 행렬의 각 행벡터(row vector)는 기하학적으로 직선을 의미하는데 이는 $\mathbf{P}$ 행렬에서 각각의 행벡터가 평면을 의미하는 것과 유사하다. $\mathbf{p}_{i,row}$ 행렬이 X,Y 축 평면과 주평면(principal plane)을 의미했다면 $\mathcal{P}$ 행렬의 행벡터는 해당 평면들의 교차선을 의미한다. 다시 말하면, $\mathcal{P}$의 행벡터는 카메라의 중심점 $\tilde{\mathbf{C}}$를 지나가며 각 $X,Y,Z$에 평행한 직선을 의미한다.
예를 들어, $\mathcal{P}$의 첫번째 행벡터는 $[\mathbf{p}_{2,row} \wedge \mathbf{p}_{3,row}]$인데 이는 $y=0$ 평면인 $\mathbf{p}_{2,row}$와 주평면 $\mathbf{p}_{3,row}$가 서로 교차하는 직선을 의미한다. 만약 3차원 공간 상의 직선 $\mathcal{L}$에 대하여 $\mathcal{PL} = 0$이면 이는 해당 직선이 $\mathcal{P}$의 영공간(null space)에 존재하는 것을 의미한다. 이는 곧 $\mathcal{L}$이 카메라 중심점 $\tilde{\mathbf{C}}$를 지나가는 것을 의미한다.
5.6.2. Point and line duality
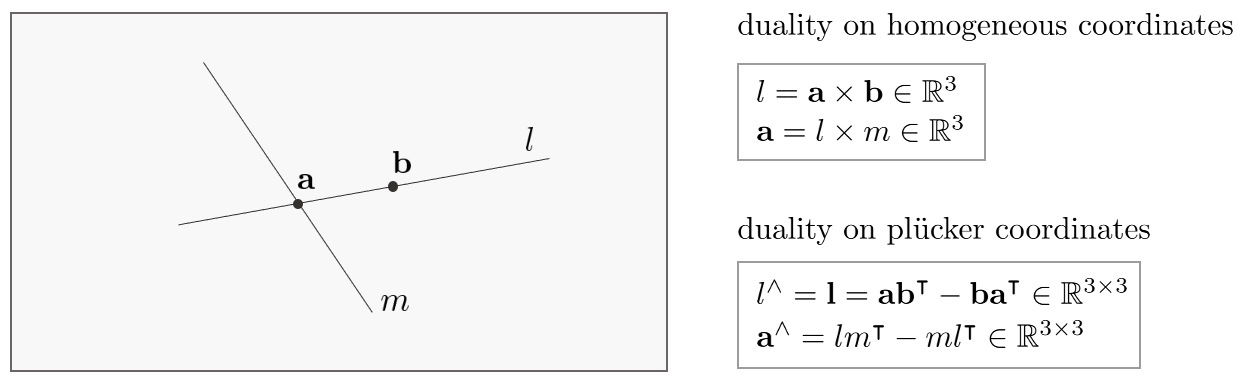
앞서 3차원 공간 상의 직선 $\mathcal{L}$ 프로젝션한 직선 $l$의 반대칭행렬은 (\ref{eq:5}) $\mathbf{l} = \mathbf{PLP}^{\intercal}$을 통해 구할 수 있다고 하였다. 이를 또한 다음과 같이 표현할 수도 있다.
\begin{equation}
\begin{aligned}
l^{\wedge} & = (\mathbf{a} \times \mathbf{b})^{\wedge} \\
& = \mathbf{ab}^{\intercal} - \mathbf{ba}^{\intercal} = \begin{bmatrix} 0&l_2&-l_{1} \\ -l_{2} & 0 & l_{0} \\ l_{1} & -l_{0} & 0 \end{bmatrix} \\
& = \mathbf{l}
\end{aligned}
\end{equation}
- $l \in \mathbb{R}^{3}$: 이미지 상의 직선
- $l^{\wedge} \in \mathbb{R}^{3\times3}$: 직선 $l$의 반대칭 행렬
- $\mathbf{a}, \mathbf{b}$: 3차원 공간 상의 점 $\mathbf{A}, \mathbf{B}$를 프로젝션한 점
외적의 성질에 의해 $\mathbf{a} = \mathbf{b} \times \mathbf{c}$ 일 때, $\mathbf{a}^{\wedge} = \mathbf{cb}^{\intercal} - \mathbf{bc}^{\intercal}$가 된다.
Duality: 3차원 공간 상의 두 직선 $\mathcal{L}, \mathcal{M}$의 프로젝션된 두 직선 $l, m$의 교차점 $\mathbf{a}$는 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{a}^{\wedge} = lm^{\intercal} - ml^{\intercal} \in \mathbb{R}^{3\times3}
\end{aligned}
\end{equation}
- $\mathbf{a}^{\wedge}$: $\mathbf{a}$의 반대칭 행렬
5.6.3. Projection matrix duality
다음으로 프로젝션 행렬 또한 duality를 가진다.
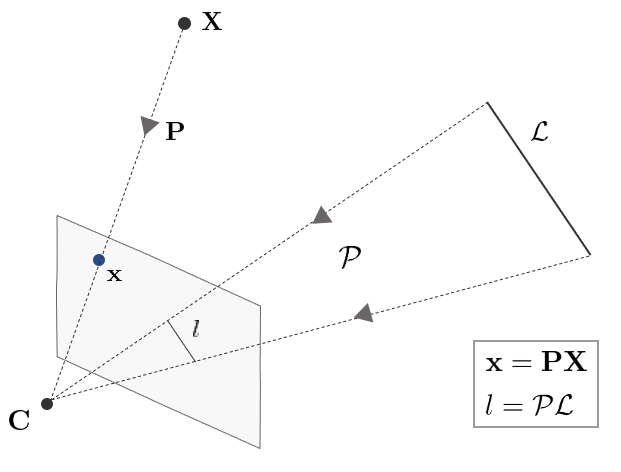
직선의 프로젝션 행렬 $\mathcal{P}$은 3차원 점의 프로젝션 행렬 $\mathbf{P}$와 동일한 기능을 수행한다.
\begin{equation}
\begin{aligned}
\mathbf{x} & = \mathbf{PX} \\ l & = \mathcal{P}\mathcal{L}
\end{aligned}
\end{equation}
6. Plücker line-based optimization
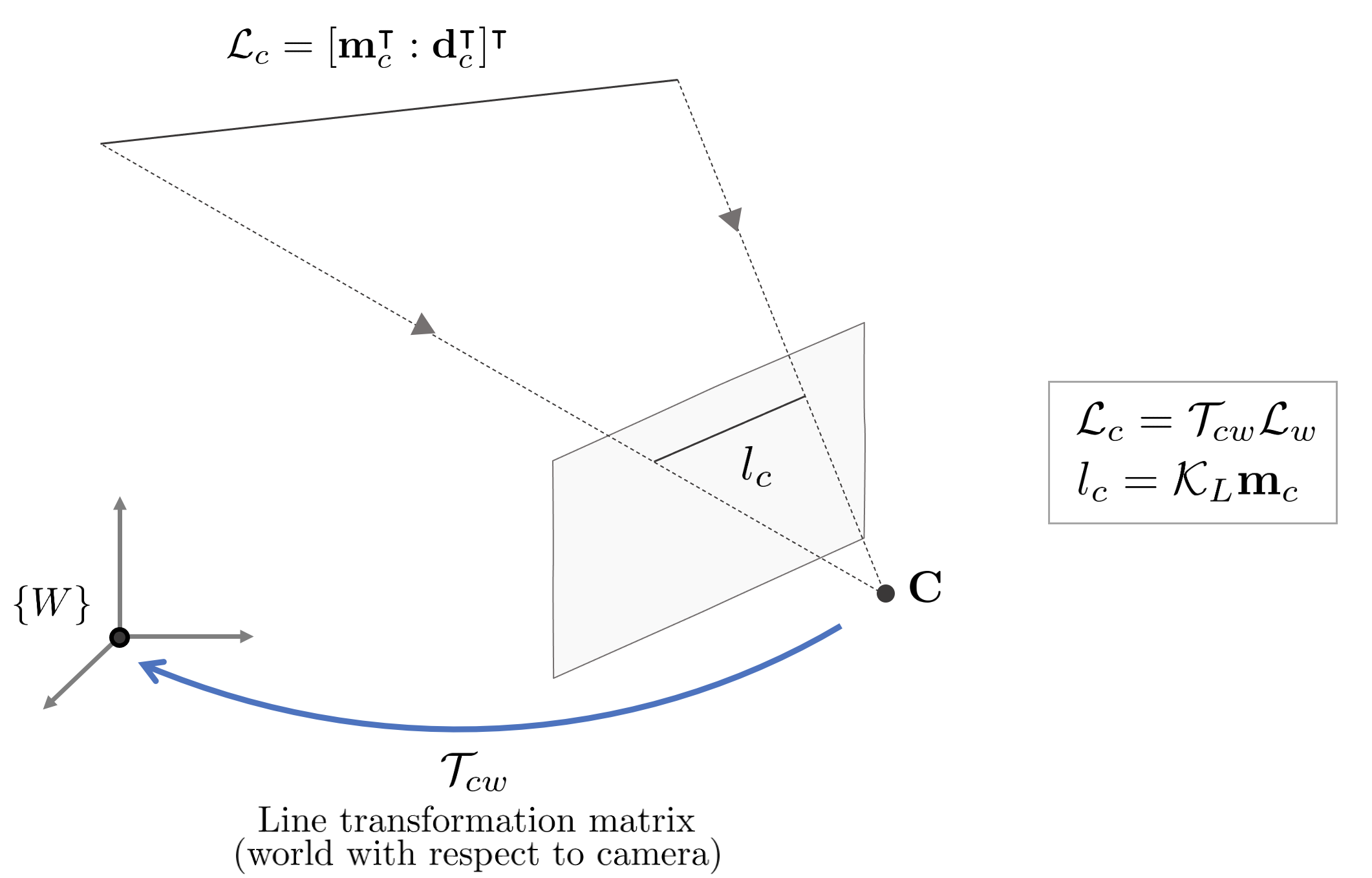
3차원 공간 상의 직선은 Plücker Coordinate를 사용하여 6차원 열벡터로 표현할 수 있다.
\begin{equation}
\begin{aligned}
\mathcal{L} & = [\mathbf{m}^{\intercal} : \mathbf{d}^{\intercal}]^{\intercal} = [ m_{x} : m_{y} : m_{z} : d_{x} : d_{y} : d_{z}]^{\intercal}
\end{aligned}
\end{equation}
앞서 설명한 $[\mathbf{d} : \mathbf{m}]$ 순서와 달리 Plücker Coordinate를 활용한 논문에서는 대부분 $[\mathbf{m} : \mathbf{d}]$ 순서를 사용하기 때문에 본 섹션에서도 해당 순서로 직선을 표현한다. 해당 직선 표현법은 스케일 모호성을 가지고 있기 때문에(up to scale) 5자유도를 가지며 $\mathbf{m}, \mathbf{d}$은 단위 벡터가 아니어도 두 벡터 값의 비율에 의해 직선을 유일하게 표현할 수 있다.
6.1. Line Transformation and projection
월드 좌표계에서 본 직선을 $\mathcal{L}_{w}$라고 하면 이를 카메라 좌표계에서 봤을 경우 다음과 같이 변환할 수 있다[8].
\begin{equation}
\begin{aligned}
\mathcal{L}_{c} & = \begin{bmatrix} \mathbf{m}_{c} \\ \mathbf{d}_{c} \end{bmatrix} = \mathcal{T}_{cw}\mathcal{L}_{w} = \begin{bmatrix} \mathbf{R}_{cw} & \mathbf{t}^{\wedge}\mathbf{R}_{cw} \\ 0 & \mathbf{R}_{cw} \end{bmatrix} \begin{bmatrix} \mathbf{m}_{w} \\ \mathbf{d}_{w} \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathcal{T}_{cw} \in \mathbb{R}^{6\times6}$: Plücker 직선의 변환 행렬
해당 직선을 이미지 평면 상에 프로젝션시키면 다음과 같다.
\begin{equation}
\begin{aligned}
l_{c} & = \begin{bmatrix} l_{1} \\ l_{2} \\ l_{3} \end{bmatrix} = \mathcal{K}_{L}\mathbf{m}_{c} = \begin{bmatrix} f_{y} && \\ &f_{x} & \\ -f_{y}c_{x} & -f_{x}c_{y} & f_{x}f_{y} \end{bmatrix} \begin{bmatrix} m_{x} \\ m_{y} \\ m_{z} \end{bmatrix}
\end{aligned}
\end{equation}
- $\mathcal{K}_{L}$: 직선의 내부 파라미터 행렬(line intrinsic matrix)
$\mathcal{K}_{L}$는 (\ref{eq:6})에서 $\mathbf{P} = K [ \mathbf{I} | \mathbf{0}]$인 경우를 의미한다. 따라서 $\mathcal{P} = [\det(\mathbf{K})\mathbf{K}^{-\intercal} | \mathbf{0}]$이 되므로 (\ref{eq:7})에서 $\mathcal{L}$의 $\mathbf{d}$ 항이 0으로 소거된다. 따라서 $\mathbf{K} = \begin{bmatrix} f_x & & c_x \\ & f_y & c_y \\ &&1 \end{bmatrix}$ 일 때 다음과 같은 식이 유도된다.
\begin{equation}
\begin{aligned}
\mathcal{K}_{L} = \det(\mathbf{K})\mathbf{K}^{-\intercal} = \begin{bmatrix} f_{y} && \\ &f_{x} & \\ -f_{y}c_{x} & -f_{x}c_{y} & f_{x}f_{y} \end{bmatrix} \in \mathbb{R}^{3\times3}
\end{aligned}
\end{equation}
6.2. Line reprojection error
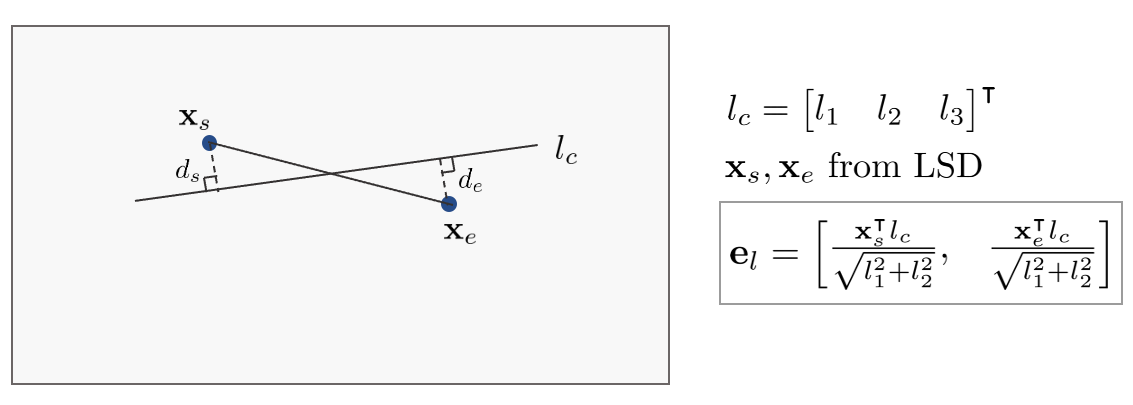
직선의 reprojection 에러 $\mathbf{e}_{l}$은 다음과 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{e}_{l} = \begin{bmatrix} d_{s}, \ d_{e} \end{bmatrix}= \begin{bmatrix} \frac{\mathbf{x}_{s}^{\intercal}l_{c}}{\sqrt{l_{1}^{2} + l_{2}^{2}}}, & \frac{\mathbf{x}_{e}^{\intercal}l_{c}}{\sqrt{l_{1}^{2} + l_{2}^{2}}}\end{bmatrix} \in \mathbb{R}^{2}
\end{aligned}
\end{equation}
이는 점과 직선 사이의 거리 공식을 통해 나타낼 수 있다. 이 때, $\{\mathbf{x}_{s}, \mathbf{x}_{e}\}$는 각각 line feature extractor(e.g., LSD)를 사용하여 추출한 직선의 시작점과 끝점을 의미한다.
6.3. Orthonormal representation
앞서 구한 $\mathbf{e}_{l}$를 사용하여 BA 최적화를 수행할 때 Plücker Coordinate 표현법을 그대로 사용하게 되면 문제가 발생한다. Plücker Coordinate는 항상 $\mathbf{m}^{\intercal}\mathbf{d} = 0$이라는 Klein quadric 제약조건을 만족해야 하기 때문에 5자유도를 가지므로 직선을 표현할 수 있는 최소 파라미터 개수인 4개의 비해 over-parameterized 되어 있다. Over-parameterized된 표현법의 단점은 다음과 같다[6].
- 중복되는 파라미터를 계산해야 하기 때문에 최적화 수행 시 연산량이 증가한다.
- 추가적인 자유도로 인해 수치적인 불안정성(numerical instability) 문제가 야기될 수 있다.
- 파라미터가 업데이트될 때마다 항상 제약조건을 만족하는 지 체크해줘야 한다.
따라서 직선을 최적화 할 때는 일반적으로 최소 파라미터인 4자유도로 변경하기 위해 orthonormal 표현법을 사용한다[4][5][6][7]. 즉, 직선을 표현할 때는 Plücker Coordinate를 사용하지만 최적화를 수행할 때는 orthonormal 표현법으로 변형한 뒤 최적값을 업데이트하고 다시 Plücker Coordinate로 돌아오는 방식을 취한다.
Orthonormal 표현법은 다음과 같다. 3차원 공간 상의 직선은 항상 다음과 같이 표현 가능하다[6].
\begin{equation}
\begin{aligned}
(\mathbf{U}, \mathbf{W}) \in SO(3) \times SO(2)
\end{aligned}
\end{equation}
- $\mathbf{U} \in SO(3)$: 3차원 직선의 회전 행렬
- $\mathbf{W} \in SO(2)$: 3차원 직선이 원점과 떨어진 거리 정보를 포함하는 행렬
임의의 Plücker 직선 $\mathcal{L} = [\mathbf{m}^{\intercal} : \mathbf{d}^{\intercal}]^{\intercal}$은 이와 일대일 대응하는 $(\mathbf{U}, \mathbf{W})$를 항상 가지고 있으며 이러한 표현 방법을 orthonormal 표현법이라고 한다. 월드 상의 한 직선 $\mathcal{L}_{w} = [ \mathbf{m}_{w}^{\intercal} : \mathbf{d}_{w}^{\intercal}]^{\intercal}$이 주어졌을 때 $\mathcal{L}_{w}$을 QR decomposition 함으로써 $(\mathbf{U}, \mathbf{W})$구할 수 있다.
\begin{equation}
\begin{aligned}
\begin{bmatrix} \mathbf{m}_{w} \ | \ \mathbf{d}_{w} \end{bmatrix}= \mathbf{U} \begin{bmatrix} w_{1} & 0\\ 0& w_{2} \\0 & 0 \end{bmatrix}, \quad \text{with set: } \mathbf{W} = \begin{bmatrix} w_{1} & -w_{2} \\ w_{2} & w_{1} \end{bmatrix}
\end{aligned}
\end{equation}
이 때, 상삼각행렬(upper triangle matrix) $\mathbf{R}$의 $(1,2)$ 원소는 Plücker 제약조건(Klein quadric)으로 인해 항상 0이 된다. $\mathbf{U}, \mathbf{W}$는 각각 3차원, 2차원 회전행렬을 의미하므로 $\mathbf{U} = \mathbf{R}(\boldsymbol{\theta}), \mathbf{W} = \mathbf{R}(\theta)$와 같이 나타낼 수 있다.
\begin{equation}
\begin{aligned}
\mathbf{R}(\boldsymbol{\theta}) & = \mathbf{U} = \begin{bmatrix} \mathbf{u}_{1} & \mathbf{u}_{2} & \mathbf{u}_{3} \end{bmatrix} = \begin{bmatrix} \frac{\mathbf{m}_{w}}{\left\| \mathbf{m}_{w} \right\|} & \frac{\mathbf{d}_{w}}{\left\| \mathbf{d}_{w} \right\|} & \frac{\mathbf{m}_{w} \times \mathbf{d}_{w}}{\left\| \mathbf{m}_{w} \times \mathbf{d}_{w} \right\|} \end{bmatrix} \\
\mathbf{R}(\theta) & = \mathbf{W} = \begin{bmatrix} w_{1} & -w_{2} \\ w_{2} & w_{1} \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \\
& = \frac{1}{\sqrt{\left\| \mathbf{m}_{w} \right\|^{2} + \left\| \mathbf{d}_{w} \right\|^{2}}} \begin{bmatrix} \left\| \mathbf{m}_{w} \right\| & \left\| \mathbf{d}_{w} \right\| \\ -\left\| \mathbf{d}_{w} \right\| & \left\| \mathbf{m}_{w} \right\| \end{bmatrix}
\end{aligned}
\end{equation}
- $\boldsymbol{\theta} \in \mathbb{R}^{3}$: SO(3) 회전행렬에 대응하는 파라미터
- $\theta \in \mathbb{R}$: SO(2) 회전행렬에 대응하는 파라미터
- $\mathbf{u}_{i}$: $i$번째 열벡터(column vector)
실제 최적화를 수행할 때는 $\mathbf{U} \leftarrow \mathbf{U}\mathbf{R}(\boldsymbol{\theta}), \mathbf{W} \leftarrow \mathbf{W}\mathbf{R}(\theta)$과 같이 업데이트된다. 따라서 orthonormal 표현법은 3차원 공간 상의 직선을 $\delta_{\boldsymbol{\theta}} = [ \boldsymbol{\theta}^{\intercal}, \theta ] \in \mathbb{R}^{4}$를 통해 4자유도로 표현할 수 있다. 최적화를 통해 업데이트된 $[ \boldsymbol{\theta}^{\intercal}, \theta ]$는 다음과 같이 $\mathcal{L}_{w}$로 변환된다.
\begin{equation}
\begin{aligned}
\mathcal{L}_{w} = \begin{bmatrix} w_{1} \mathbf{u}_{1}^{\intercal} & w_{2} \mathbf{u}_{2}^{\intercal} \end{bmatrix}
\end{aligned}
\end{equation}
6.4. Error function formulation
직선에 대한 reprojection 에러 $\mathbf{e}_{l}$를 최적화하기 위해서는 Gauss-Newton(GN), Levenberg-Marquardt(LM) 등의 비선형 최소제곱법을 사용하여 반복적으로(iterative) 최적 변수를 업데이트해야 한다. reprojection 에러를 사용하여 에러 함수를 표현하면 다음과 같다.
\begin{equation}
\begin{aligned}
\mathbf{E}_{l}(\mathcal{X}) & = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \left\| \mathbf{e}_{l,ij} \right\|^{2} \\
& = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \mathbf{e}_{l,ij}^{\intercal}\mathbf{e}_{l,ij} \\
\end{aligned} \label{eq:10}
\end{equation}
- $\mathcal{X} = [\delta_{\boldsymbol{\theta}}, \delta_\xi ]$: 상태 변수
- $\delta_{\boldsymbol{\theta}} = [ \boldsymbol{\theta}^{\intercal}, \theta ] \in \mathbb{R}^{4}$: orthonormal 표현법의 상태 변수
- $\delta_{\xi} = [\delta \xi] \in se(3)$: Lie theory를 통한 업데이트 방법은 해당 링크를 참조하면 된다
$\mathbf{E}_{l}(\mathcal{X}^{*})$를 만족하는 $\left\|\mathbf{e}_{l}(\mathcal{X}^{*})\right\|^{2}$를 non-linear least squares를 통해 반복적으로 계산할 수 있다. 작은 증분량 $\Delta \mathcal{X}$를 반복적으로 $\mathcal{X}$에 업데이트함으로써 최적의 상태를 찾는다.
\begin{equation}
\begin{aligned}
\mathbf{E}_{l}(\mathcal{X} + \Delta \mathcal{X}) & = \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \left\|\mathbf{e}_{l}(\mathcal{X} +\Delta \mathcal{X})\right\|^{2}
\end{aligned}
\end{equation}
엄밀하게 말하면 상태 증분량 $\Delta \mathcal{X}$은 SE(3) 변환행렬을 포함하므로 $\oplus$ 연산자를 통해 기존 상태 $\mathcal{X}$에 더해지는게 맞지만 표현의 편의를 위해 $+$ 연산자를 사용하였다.
\begin{equation}
\begin{aligned}
\mathbf{e}_{l}( \mathcal{X} \oplus \Delta \mathcal{X})
\quad \rightarrow \quad\mathbf{e}_{l}(\mathcal{X} + \Delta \mathcal{X})
\end{aligned}
\end{equation}
- $\oplus$ : 상태 변수 $\delta_{\boldsymbol{\theta}}, \delta_\xi$를 한 번에 업데이트할 수 있는 연산자.
위 식은 테일러 1차 근사를 통해 다음과 같이 표현이 가능하다.
\begin{equation}
\begin{aligned}
\mathbf{e}_{l}(\mathcal{X} + \Delta \mathcal{X}) & \approx \mathbf{e}_{l}(\mathcal{X}) + \mathbf{J}\Delta \mathcal{X} \\ & = \mathbf{e}_{l}(\mathcal{X}) + \mathbf{J}_{\boldsymbol{\theta}} \Delta \delta_{\boldsymbol{\theta}} +\mathbf{J}_{\xi} \Delta \delta_\xi \\
& = \mathbf{e}_{l}(\mathcal{X}) + \frac{\partial \mathbf{e}_{l}}{\partial \delta_{\boldsymbol{\theta}}} \Delta \delta_{\boldsymbol{\theta}} + \frac{\partial \mathbf{e}_{l}}{\partial \delta_\xi}\Delta \delta_\xi \\
\end{aligned}
\end{equation}
- $\mathbf{J} = \frac{\partial \mathbf{e}_{l}}{\partial \mathcal{X}} = \frac{\partial \mathbf{e}_{l}}{\partial [\delta_{\boldsymbol{\theta}}, \delta_\xi]}$
\begin{equation}
\begin{aligned}
\mathbf{E}_{l}(\mathcal{X} + \Delta \mathcal{X}) & \approx \arg\min_{\mathcal{X}^{*}} \sum_{i}\sum_{j} \left\|\mathbf{e}_{l}(\mathcal{X}) + \mathbf{J}\Delta \mathcal{X} \right\|^{2} \\
\end{aligned}
\end{equation}
이를 미분하여 최적의 증분량 $\Delta \mathcal{X}^{*}$ 값을 구하면 다음과 같다. 자세한 유도 과정은 본 문서에서는 생략한다. 유도 과정에 대해 자세히 알고 싶으면 해당 링크을 참조하면 된다.
\begin{equation}
\begin{aligned}
& \mathbf{J}^{\intercal}\mathbf{J} \Delta \mathcal{X}^{*} = -\mathbf{J}^{\intercal}\mathbf{e} \\
& \mathbf{H}\Delta \mathcal{X}^{*} = - \mathbf{b} \\
\end{aligned}
\end{equation}
6.4.1. The analytical jacobian of 3d line
이전 섹션에서 설명한 것처럼 비선형 최적화를 수행하기 위해서는 $\mathbf{J}$를 계산해야 한다. $\mathbf{J}$는 다음과 같이 구성되어 있다.
\begin{equation}
\begin{aligned}
& \mathbf{J} = [ \mathbf{J}_{\boldsymbol{\theta}}, \mathbf{J}_{\xi} ]
\end{aligned}
\end{equation}
$[ \mathbf{J}_{\boldsymbol{\theta}}, \mathbf{J}_{\xi} ]$는 다음과 같이 전개할 수 있다.
\begin{equation}
\begin{aligned}
& \mathbf{J}_{\boldsymbol{\theta}} = \frac{\partial \mathbf{e}_{l}}{\partial \delta_{\boldsymbol{\theta}}} = \frac{\partial \mathbf{e}_{l}}{\partial l} \frac{\partial l}{\partial \mathcal{L}_{c}} \frac{\partial \mathcal{L}_{c}}{\partial \mathcal{L}_{w}} \frac{\partial \mathcal{L}_{w}}{\partial \delta_{\boldsymbol{\theta}}} \\
& \mathbf{J}_{\xi} = \frac{\partial \mathbf{e}_{l}}{\partial \delta_{\xi}} = \frac{\partial \mathbf{e}_{l}}{\partial l} \frac{\partial l}{\partial \mathcal{L}_{c}} \frac{\partial \mathcal{L}_{c}}{\partial \delta_{\xi}}
\end{aligned}
\end{equation}
$\frac{\partial \mathbf{e}_{l}}{\partial l}$는 다음과 같이 구할 수 있다. 이 때, $l$은 벡터이고 $l_{i}$는 스칼라임에 유의한다.
\begin{equation}
\begin{aligned}
\frac{\partial \mathbf{e}_{l}}{\partial l} = \frac{1}{\sqrt{l_{1}^{2} + l_{2}^{2}}} \begin{bmatrix} x_{s} - \frac{l_{1} \mathbf{x}_{s}l}{\sqrt{l_{1}^{2} + l_{2}^{2}}} & y_{s} - \frac{l_{2} \mathbf{x}_{s}l}{\sqrt{l_{1}^{2} + l_{2}^{2}}} & 1 \\
x_{e} - \frac{l_{1} \mathbf{x}_{e}l}{\sqrt{l_{1}^{2} + l_{2}^{2}}} & y_{e} - \frac{l_{2} \mathbf{x}_{e}l}{\sqrt{l_{1}^{2} + l_{2}^{2}}} & 1 \end{bmatrix} \in \mathbb{R}^{2\times3}
\end{aligned}
\end{equation}
$\frac{\partial l}{\partial \mathcal{L}_{c}}$는 다음과 같이 구할 수 있다.
\begin{equation}
\begin{aligned}
\frac{\partial l}{\partial \mathcal{L}_{c}} = \frac{\partial \mathcal{K}_{L}\mathbf{m}_{c}}{\partial \mathcal{L}_{c}} = \begin{bmatrix} \mathcal{K}_{L} & \mathbf{0}_{3\times3} \end{bmatrix} = \begin{bmatrix} f_{y} && & 0 &0&0 \\ &f_{x} & & 0 &0&0 \\ -f_{y}c_{x} & -f_{x}c_{y} & f_{x}f_{y} & 0 &0&0 \end{bmatrix} \in \mathbb{R}^{3\times6}
\end{aligned}
\end{equation}
$\frac{\partial \mathcal{L}_{c}}{\partial \mathcal{L}_{w}}$는 다음과 같이 구할 수 있다.
\begin{equation}
\begin{aligned}
\frac{\partial \mathcal{L}_{c}}{\partial \mathcal{L}_{w}} = \frac{\partial \mathcal{T}_{cw}\mathcal{L}_{w}}{\partial \mathcal{L}_{w}}= \mathcal{T}_{cw} = \begin{bmatrix} \mathbf{R}_{cw} & \mathbf{t}^{\wedge}\mathbf{R}_{cw} \\ 0 & \mathbf{R}_{cw} \end{bmatrix} \in \mathbb{R}^{6\times6}
\end{aligned}
\end{equation}
orthonormal 표현법에 대한 자코비안 $\frac{\partial \mathcal{L}_{w}}{\partial \delta_{\boldsymbol{\theta}}}$는 다음과 같이 구할 수 있다[8].
\begin{equation}
\begin{aligned}
\frac{\partial \mathcal{L}_{w}}{\partial \delta_{\boldsymbol{\theta}}} = \begin{bmatrix} \mathbf{0}_{3\times1} & -w_{1}\mathbf{u}_{3} & w_{1}\mathbf{u}_{2} & -w_{2}\mathbf{u}_{1} \\ w_{2}\mathbf{u}_{3} & \mathbf{0}_{3\times1} & -w_{2}\mathbf{u}_{1} & w_{1}\mathbf{u}_{2} \end{bmatrix} \in \mathbb{R}^{6 \times 4}
\end{aligned}
\end{equation}
카메라 포즈에 대한 자코비안 $\frac{\partial \mathcal{L}_{c}}{\partial \delta_{\xi}}$는 다음과 같이 구할 수 있다[9].
\begin{equation}
\begin{aligned}
\frac{\partial \mathcal{L}_{c}}{\partial \delta_{\xi}} = \begin{bmatrix} -(\mathbf{R}\mathbf{m})^{\wedge} - (\mathbf{t}^{\wedge} \mathbf{Rd})^{\wedge} & -(\mathbf{Rd})^{\wedge} \\ -(\mathbf{Rd})^{\wedge} & \mathbf{0}_{3\times3} \end{bmatrix} \in \mathbb{R}^{6 \times 6}
\end{aligned}
\end{equation}
7. References
[3] [Wiki] Plücker Coordinates
'Fundamental' 카테고리의 다른 글
| 다중관점기하학(Multiple View Geometry in Computer Vision) 책 내용 정리 Part 2 (1) | 2022.01.05 |
|---|---|
| 다중관점기하학(Multiple View Geometry in Computer Vision) 책 내용 정리 Part 1 (5) | 2022.01.05 |
| 선형대수학 (Linear Algebra) 개념 정리 Part 1 (1) | 2022.01.05 |
| 리군 이론(Lie Theory) 개념 정리 - SO(3), SE(3) (9) | 2022.01.04 |
| 오일러 각도 (Euler Angle) 개념 정리 (0) | 2022.01.04 |
 A L I D A
A L I D A





