선형대수학 (Linear Algebra) 개념 정리 Part 1

 
본 포스트는 선형대수학의 전반적인 내용에 대해 간락히 정리한 내용이다. 대부분의 내용은 인공지능을 위한 선형대수 - 주재걸 교수님 (edwith) 영상을 참고하여 제작하였다.

선형대수학 (Linear Algebra) 개념 정리 Part 2 는 주로 행렬대수학과 관련된 내용을 다룬다.
확률 이론에 대한 내용을 알고싶으면 확률 이론(Probability Theory) 개념 정리 포스트를 참조하면 된다.

 

Chapter 1 - Linear Systems

Linear Equation

선형방정식(Linear Equation)은 변수 $x_1,\cdots ,x_n$이 있을 때 다음과 같이 작성할 수 있는 방정식을 의미한다.
$$\begin{array}{}\text{(1)}& \begin{array}{r}{a}_1{x}_1+a_2{x}_2+\cdots +a_n{x}_n=b\end{array}\end{array}$$
이 때, $b$는 계수를 의미하고 $a_1,\cdots ,a_n$ 값들은 실수 또는 복소수의 미지수를 의미한다. 위 식은 다음과 같이 간결하게 작성할 수 있다.
$$\begin{array}{}\text{(2)}& \begin{array}{r}{\mathbf{a}}^T\mathbf{x}=b\end{array}\end{array}$$
이 때, $\mathbf{a}=\left[\begin{array}{c}{a}_1\\ ⋮\\ a_n\end{array}\right]$이고 $\mathbf{x}=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_n\end{array}\right]$이다.

 

Linear system

선형방정식(linear equation)의 집합을 선형시스템(linear system)이라고 한다. n개의 선형방정식 ${\mathbf{a}}_1\mathbf{x}=b_1,\cdots ,{\mathbf{a}}_n\mathbf{x}=b_n$ 이 있는 경우 이를 다음과 같이 간결하게 선형시스템으로 표현할 수 있다.
$$\begin{array}{}\text{(3)}& \begin{array}{r}\mathbf{Ax}=\mathbf{b}\end{array}\end{array}$$

즉, $\mathbf{Ax}=\mathbf{b}$ 형태의 행렬과 벡터의 방정식을 선형시스템이라고 한다. 선형시스템은 다른 말로 비동차방정식이라고도 불린다. 동차방정식, 비동차방정식의 정의는 다음과 같다.

Homogeneous equation

동차방정식(homogeneous equation)은 $\mathbf{A}\in {\mathbb{R}}^{n\times m},\mathbf{x}\in {\mathbb{R}}^{m\times 1},\mathbf{b}\in {\mathbb{R}}^{m\times 1}$ 일 때, $\mathbf{Ax}=0$ 형태의 시스템을 말한다. 0이 아닌 해가 존재한다. 이와 반대로 $\mathbf{Ax}=\mathbf{b}$ 형태의 방정식을 비동차방정식(non-homogeneous equation)이라고 한다. 비동차방정식은 해가 존재하지 않거나 여러 개 존재한다.

 

Over-determined system

Over-determined 시스템은 방정식의 개수가 미지수의 개수보다 많은 경우를 의미한다. $\mathbf{Ax}=\mathbf{b}$ 의 형태에서 $\mathbf{A}\in {\mathbb{R}}^{m\times n},\mathbf{x}\in {\mathbb{R}}^{n\times 1},\mathbf{b}\in {\mathbb{R}}^{m\times 1}$ 이라고 했을 때 $m>n$ 인 경우를 의미한다. Over-determined 시스템의 경우 해가 존재하지 않으며 full column rank를 가진다. 

$\mathbf{Ax}=\mathbf{b}$ 시스템의 해가 존재하지 않으므로 $\Vert \mathbf{Ax}-\mathbf{b}\Vert$을 최소화하는 근사해를 구하는 방법을 주로 사용한다.

 

Under-determined system

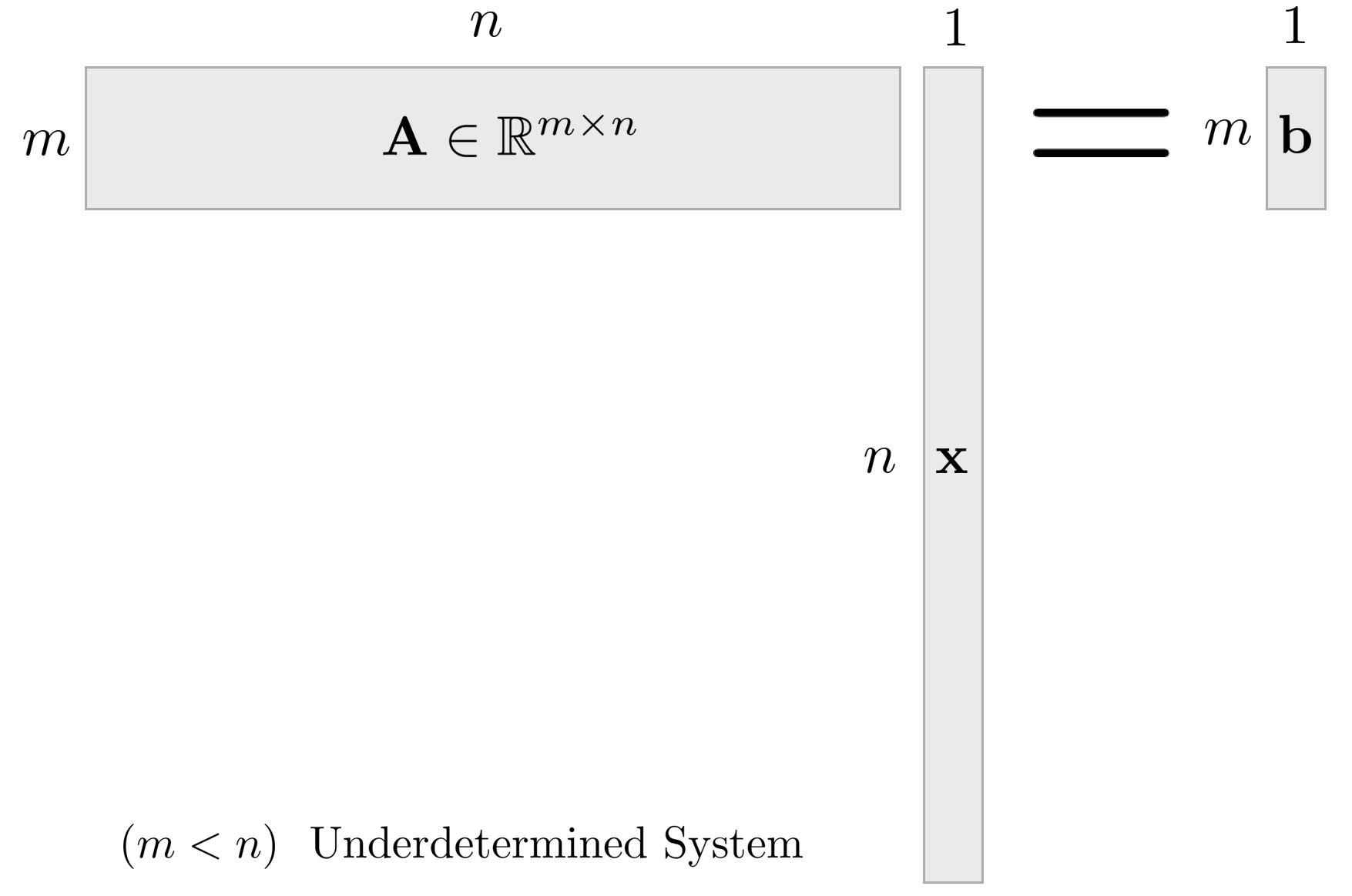
Under-determined 시스템의 경우 방정식의 개수보다 미지수의 개수가 많은 경우를 의미한다. 즉, over-determined 시스템과 반대로 $n>m$ 인 경우를 의미한다. Under-determined 시스템의 경우 무수히 많은 해가 존재하며 full row rank를 가진다. 

$\mathbf{Ax}=\mathbf{b}$ 시스템이 무수히 많은 해를 가지므로 ${\Vert \mathbf{x}\Vert }^2$ 가 최소가 되는 해를 구하는 방법을 주로 사용한다.

 

Solving Linear System

행렬 $\mathbf{A}$의 역행렬이 존재하는 경우 선형시스템은 역행렬을 사용하여 다음과 같이 풀 수 있다.
$$\begin{array}{}\text{(4)}& \begin{array}{rl}& \mathbf{Ax}=\mathbf{b}\\ & {\mathbf{A}}^{-1}\mathbf{Ax}={\mathbf{A}}^{-1}\mathbf{b}\\ & \mathbf{Ix}={\mathbf{A}}^{-1}\mathbf{b}\\ & \mathbf{x}={\mathbf{A}}^{-1}\mathbf{b}\end{array}\end{array}$$
그러나, 행렬 $\mathbf{A}$의 판별식 $det\mathbf{A}=0$인 경우 역행렬이 존재하지 않게되고 위와 같이 문제를 풀 수 없다. 이런 경우 선형시스템은 해가 존재하지 않거나 무수히 많은 해가 존재한다.

Linear Combination

여러 벡터 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n\in {\mathbb{R}}^n$이 있을 때 스칼라 값 $c_1,\cdots ,c_n$에 대하여
$$\begin{array}{}\text{(5)}& \begin{array}{r}{c}_1{\mathbf{v}}_1+\cdots +c_n{\mathbf{v}}_n\end{array}\end{array}$$
을 벡터 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$의 가중치 계수 $c_1,\cdots ,c_n$에 대한 선형결합 (Linear Combination) 이라고 한다. 이 때 가중치 계수 $c_1,\cdots ,c_n$는 0을 포함한 실수 값을 가진다.

Span

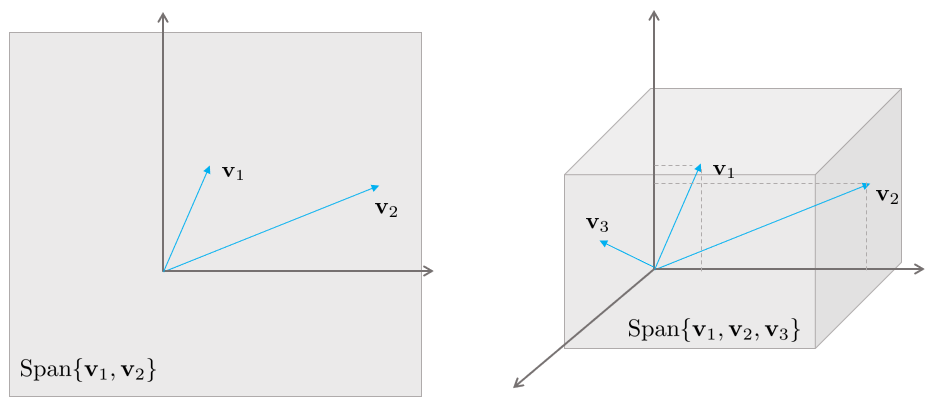
주어진 여러 벡터 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n\in {\mathbb{R}}^n$에 대해 스팬(Span) $\{{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n\}$은 모든 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$에 대한 선형결합의 집합을 의미한다. 즉, Span$\{{\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n\}$은 다음과 같이 쓸 수 있는 모든 벡터들의 집합이다.
$$\begin{array}{}\text{(6)}& \begin{array}{r}{c}_1{\mathbf{v}}_1+\cdots +c_n{\mathbf{v}}_n\end{array}\end{array}$$
이는 또한 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$에 의해 span된 ${\mathbb{R}}^n$ 공간 상의 subset이라고도 불린다.

From Matrix Equation to Vector Equation

$\mathbf{Ax}=\mathbf{b}$와 같은 선형 시스템을 다음과 같이 열벡터 ${\mathbf{a}}_i$ 를 기준으로 펼쳐보면
$$\begin{array}{}\text{(7)}& \begin{array}{r}\left[\begin{array}{cccc}{\mathbf{a}}_1& {\mathbf{a}}_2& \cdots & {\mathbf{a}}_n\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]=\mathbf{b}\end{array}\end{array}$$
로 나타낼 수 있고 이를 다시 표현하면
$$\begin{array}{}\text{(8)}& \begin{array}{r}{\mathbf{a}}_1{x}_1+{\mathbf{a}}_2{x}_2+\cdots +{\mathbf{a}}_n{x}_n=\mathbf{b}\end{array}\end{array}$$
와 같이 열벡터들의 선형결합으로 표현할 수 있게 된다. 만약 $\mathbf{b}$가 Span $\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_n\}$에 포함되어 있다면 이들의 선형결합으로 표현할 수 있으므로 해가 존재한다. 따라서 $\mathbf{b}\in \text{Span}\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_n\}$일 때 해가 존재한다.

Several Perspectives about Matrix Multiplication

선형시스템 $\mathbf{Ax}=\mathbf{b}$가 있을 때 이는 곧 $\mathbf{A}$의 열벡터들의 선형결합으로 표현할 수 있다.
$$\begin{array}{}\text{(9)}& \begin{array}{r}\mathbf{Ax}=[{\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]={\mathbf{a}}_1{x}_1+{\mathbf{a}}_2{x}_2+\cdots +{\mathbf{a}}_n{x}_n=\mathbf{b}\end{array}\end{array}$$
만약 선형시스템에 전치행렬을 적용하여 ${\mathbf{x}}^T{\mathbf{A}}^T={\mathbf{b}}^T$가 되면
$$\begin{array}{}\text{(10)}& \begin{array}{r}\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]\left[\begin{array}{c}{\mathbf{a}}_1\\ {\mathbf{a}}_2\\ ⋮\\ {\mathbf{a}}_n\end{array}\right]={\mathbf{a}}_1{x}_1+{\mathbf{a}}_2{x}_2+\cdots +{\mathbf{a}}_n{x}_n=\mathbf{b}\end{array}\end{array}$$
${\mathbf{b}}^T$는 곧 ${\mathbf{A}}^T$의 행벡터(Row Vector)들의 선형결합으로 표현된다.
또한 두 벡터의 곱 $\mathbf{a}{\mathbf{b}}^T=\left[\begin{array}{c}{a}_1\\ ⋮\\ a_n\end{array}\right]\left[\begin{array}{ccc}{b}_1& \cdots & b_n\end{array}\right]$의 경우 rank1 outer product 로 볼 수 있다. 즉, $[\mathbf{a}\mathbf{c}]\left[\begin{array}{c}\mathbf{b}\\ \mathbf{d}\end{array}\right]$의 경우 $\mathbf{ab}+\mathbf{cd}$ 와 같이 벡터곱을 스칼라 곱과 같이 생각할 수 있다.

Linear Independence

벡터 집합 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n\in {\mathbb{R}}^n$가 주어졌을 때, 이들 중 부분 벡터들의 집합 $\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_{j-1}\}$이 선형결합을 통해 특정 벡터 ${\mathbf{v}}_j,j=1,\cdots ,n$를 표현할 수 있는지 검사한다.
$$\begin{array}{}\text{(11)}& \begin{array}{r}{\mathbf{v}}_j\in \text{Span}\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_{j-1}\}\text{for some }j=1,\cdots ,n?\end{array}\end{array}$$

만약 ${\mathbf{v}}_j$가 선형결합으로 표현이 된다면 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$는 선형의존 (Linearly Dependent) 이다. 만약, ${\mathbf{v}}_j$가 표현되지 않는다면 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$는 선형독립 (Linearly Independent) 이다.

만약 $x_1{\mathbf{v}}_1+x_2{\mathbf{v}}_2+\cdots +x_n{\mathbf{v}}_n=\mathbf{0}$ 같은 동차(homogeneous) 선형방정식이 있다고 하면
$$\begin{array}{}\text{(12)}& \begin{array}{r}\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\end{array}\right]\end{array}\end{array}$$
과 같은 자명해가 존재한다. 이 때, ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$가 선형독립이면 자명해 이외에 해는 존재하지 않는다. 하지만, ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$가 선형의존이면 선형시스템은 자명해 이외에 다른 해가 존재한다.
자명해 이외에 다른 해가 존재하는 선형의존(Linearly Dependent) 경우 대해서 생각해보면 예를 들어 $\mathbf{A}$ 행렬이 다음과 같이 5개의 열을 가진 행렬이라고 했을 때
$$\begin{array}{}\text{(13)}& \begin{array}{r}\mathbf{A}=\left[\begin{array}{ccccc}{\mathbf{a}}_1& {\mathbf{a}}_2& {\mathbf{a}}_3& {\mathbf{a}}_4& {\mathbf{a}}_5\end{array}\right]\end{array}\end{array}$$
위 열벡터(Column Vector)들 중 최소한 두 개 이상의 벡터가 선형결합 되어야 동차방정식 $\mathbf{Ax}=\mathbf{0}$의 해를 만족할 수 있다. 예를 들어 ${\mathbf{a}}_2{x}_2$ 성분이 0이 아닌 경우 이를 다시 영벡터로 만들기 위해서는 다른 1,3,4,5 열벡터들의 선형결합이 $-{\mathbf{a}}_2{x}_2$의 값을 만들어야 한다. 이는 곧 ${\mathbf{a}}_2{x}_2$ 값을 다른 열벡터들의 선형결합으로 표현할 수 있다는 말과 동치이므로 선형의존인 경우 어떤 하나의 벡터가 다른 벡터들의 선형결합으로 표현될 수 있음을 의미한다. 이를 수식으로 표현하면 다음과 같다.
$$\begin{array}{}\text{(14)}& \begin{array}{rl}& {\mathbf{a}}_j{x}_j=-{\mathbf{a}}_1{x}_1-\cdots -{\mathbf{a}}_{j-1}{x}_{j-1}\\ & {\mathbf{a}}_j=-\frac{x_1}{x_j}{\mathbf{a}}_1-\cdots -\frac{x_{j-1}}{x_j}{\mathbf{a}}_{j-1}\in \text{Span}\{{\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_{j-1}\}\end{array}\end{array}$$

Linear Dependence

행렬 $\mathbf{A}$의 열벡터 ${\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n$이 선형의존(Linearly Dependent)인 경우 해당 열벡터들은 Span의 차원을 늘리지 않는다.만약 $\mathbf{A}\in {\mathbb{R}}^{3\times 3}$이고 ${\mathbf{a}}_3\in \text{Span}\{{\mathbf{a}}_1,{\mathbf{a}}_2\}$인 경우
$$\begin{array}{}\text{(15)}& \begin{array}{r}\text{Span}\{{\mathbf{a}}_1,{\mathbf{a}}_2\}=\text{Span}\{{\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3\}\end{array}\end{array}$$
만약 ${\mathbf{a}}_3=d_1{\mathbf{a}}_1+d_2{\mathbf{a}}_2$와 같이 선형결합으로 표현이 가능한 경우, ${\mathbf{a}}_1,{\mathbf{a}}_2,{\mathbf{a}}_3$는 다음과 같이 작성할 수 있다.
$$\begin{array}{}\text{(16)}& \begin{array}{r}{c}_1{\mathbf{a}}_1+c_2{\mathbf{a}}_2+c_3{\mathbf{a}}_3=(c_1+d_1){\mathbf{a}}_1+(c_1+d_1){\mathbf{a}}_2\end{array}\end{array}$$

Span and Subspace

${\mathbb{R}}^n$ 공간의 부분공간(Subspace) H는 ${\mathbb{R}}^n$의 부분집합들의 선형결합에 대해 닫혀 있는 공간을 의미한다. 즉, 두 벡터 ${\mathbf{u}}_1,{\mathbf{u}}_2\in H$일 때, 어떠한 스칼라 값 $c,d$에 대하여 $c{\mathbf{u}}_1+d{\mathbf{u}}_2\in H$일 때 H를 부분공간이라고 한다.
Span $\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_n\}$으로 형성된 공간은 항상 부분공간이다. 만약 ${\mathbf{u}}_1=x_1{\mathbf{a}}_1+\cdots +x_n{\mathbf{a}}_n$이고 ${\mathbf{u}}_2=y_1{\mathbf{a}}_1+\cdots +y_n{\mathbf{a}}_n$일 때
$$\begin{array}{}\text{(17)}& \begin{array}{rl}c{\mathbf{u}}_1+d{\mathbf{u}}_2& =c(x_1{\mathbf{a}}_1+\cdots +x_n{\mathbf{a}}_n)+d(y_1{\mathbf{a}}_1+\cdots +x_n{\mathbf{a}}_n)\\ & =(c{x}_1+d{y}_1){\mathbf{a}}_1+\cdots +(c{x}_n+d{y}_n){\mathbf{a}}_n\end{array}\end{array}$$
과 같이 선형결합으로 나타낼 수 있고 이는 임의의 값 $c,d$에 대해서 닫혀 있음을 의미한다. 따라서 부분공간은 항상 Span $\{{\mathbf{a}}_1,\cdots ,{\mathbf{a}}_n\}$으로 표현된다.

Basis of a Subspace

부분공간 H의 기저(basis) 는 다음을 만족하는 벡터들의 집합을 의미한다.

• 부분공간 H를 모두 Span할 수 있어야 한다.
• 벡터들 간 선형독립이어야 한다.

3차원 공간 ${\mathbb{R}}^3$ 의 경우 기저벡터는 3개가 존재하고 ${\mathbf{e}}_1=[100{]}^T,{\mathbf{e}}_2=[010{]}^T,{\mathbf{e}}_3=[001{]}^T$일 때, 이를 표준기저벡터(Standard Basis Vector)라고 한다.

Dimension of Subspace

하나의 부분공간 H를 표현할 수 있는 기저는 유일하지 않다. 하지만 여러개의 기저를 통해서 표현할 수 있는 부분공간의 차원(Dimension)은 유일하다. 부분공간의 차원은 기저벡터의 개수와 동일하다.

Column Space of Matrix

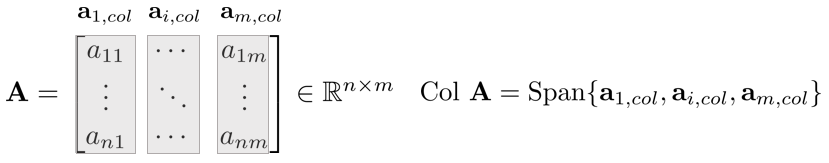
행렬 $\mathbf{A}$의 열공간(Column Space)이란 $\mathbf{A}$의 열벡터로 인해 Span된 부분공간을 의미한다. 일반적으로 Col $\mathbf{A}$라고 표기한다.
$$\begin{array}{}\text{(18)}& \begin{array}{r}\text{Col}\mathbf{A}=\text{Span}\{\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right],\left[\begin{array}{c}1\\ 0\\ 1\end{array}\right]\}\end{array}\end{array}$$

Rank of Matrix

행렬 $\mathbf{A}$의 rank란 $\mathbf{A}$의 열벡터들의 차원을 의미한다.
$$\begin{array}{}\text{(19)}& \begin{array}{r}\text{rank}\mathbf{A}=\text{dim Col}\mathbf{A}\end{array}\end{array}$$

Transformation

변환(Transformation), 함수(Function), 매핑(Mapping) $T$ 은 입력 $x$를 출력 $y$로 매핑해주는 것을 의미한다.
$$\begin{array}{}\text{(20)}& \begin{array}{r}T:x\mapsto y\end{array}\end{array}$$
이 때 입력 $x$에 의해 매핑되는 출력 $y$는 유일하게 결정된다. 정의역(Domain) 이란 입력 $x$ 의 모든 가능한 집합을 의미한다. 공역(Co-Domain) 이란 출력 $y$의 모든 가능한 집합을 의미한다. Image 란 주어진 입력 $x$에 대해 매핑된 출력 $y$를 의미한다. 치역(Range) 란 Domain내에 있는 입력 $x$들에 의해 매핑된 모든 출력 $y$의 집합을 의미한다.

Linear Transformation

변환 T는 다음과 같은 경우에 선형변환(Linear Transformation)이라고 한다.
$$\begin{array}{}\text{(21)}& \begin{array}{rl}& T(c\mathbf{u}+d\mathbf{v})=cT(\mathbf{u})+vT(\mathbf{v})\\ & \text{for all }\mathbf{u}\mathbf{,}\mathbf{v}\text{in the domain of T and for all scalars c and d.}\end{array}\end{array}$$

Transformations between Vectors

$T:\mathbf{x}\in {\mathbb{R}}^n\mapsto \mathbf{y}\in {\mathbb{R}}^m$은 n차원의 벡터를 m차원의 벡터로 매핑하는 연산을 의미한다. 예를 들면
$$\begin{array}{}\text{(22)}& \begin{array}{rl}& T:\mathbf{x}\in {\mathbb{R}}^3\mapsto \mathbf{y}\in {\mathbb{R}}^2\\ & \mathbf{x}=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]\in {\mathbb{R}}^3\mapsto \mathbf{y}=T(\mathbf{x})=\left[\begin{array}{c}4\\ 5\end{array}\right]\in {\mathbb{R}}^2\end{array}\end{array}$$

Matrix of Linear Transformation

변환 $T:{\mathbb{R}}^n\mapsto {\mathbb{R}}^m$을 선형변환이라고 가정하면 $T$는 항상 행렬과 벡터의 곱으로 표현할 수 있다. 즉,
$$\begin{array}{}\text{(23)}& \begin{array}{r}T(\mathbf{x})=\mathbf{Ax}\text{for all }\mathbf{x}\in {\mathbb{R}}^n\end{array}\end{array}$$
행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$인 경우 $\mathbf{A}$의 j번째 열 ${\mathbf{a}}_j$는 벡터 $T({\mathbf{e}}_j)$와 같다. 이 때 ${\mathbf{e}}_j$는 항등행렬 $\mathbf{I}\in {\mathbb{R}}^{n\times n}$의 j번째 열벡터이다.
$$\begin{array}{}\text{(24)}& \begin{array}{r}\mathbf{A}=[T({\mathbf{e}}_1)\cdots T({\mathbf{e}}_n)]\end{array}\end{array}$$
이러한 행렬 $\mathbf{A}$를 선형변환 T의 표준행렬(Standard Matrix)이라고 부른다.

Onto and One-To-One

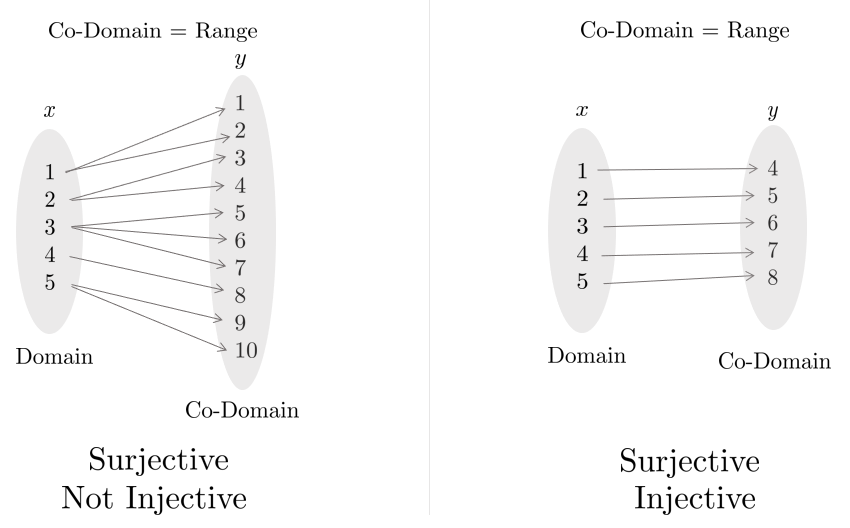
Onto는 전사함수(Surjective)라고도 불리며 공역이 치역과 같은 경우를 의미한다. 이는 Co-Domain의 모든 원소들이 사영된 것을 의미한다.
$$\begin{array}{}\text{(25)}& \begin{array}{r}\text{Surjective: Co-Domain = Range}\end{array}\end{array}$$
One-To-One은 일대일함수(Injective)라고도 불리며 정의역의 원소와 공역의 원소가 하나씩 대응되는 함수를 의미한다.

 

Chapter 2 - Least Squares

Least Squares

최소제곱법(Least Squares)는 방정식의 개수가 미지수의 개수보다 많은 Overdetermined 선형시스템에서 사용하는 방법 중 하나이다. Overdetermined 선형시스템 $\mathbf{Ax}=\mathbf{b}$의 경우 일반적으로 해가 존재하지 않는다. 이런 경우 일반적으로 ${\Vert \mathbf{Ax}-\mathbf{b}\Vert }^2$가 최소가 되는 근사해를 구할 수 있다.
 

Inner Product

벡터 $\mathbf{u}\mathbf{,}\mathbf{v}\in {\mathbb{R}}^n$에 대해 이를 각각 $n\times 1$의 행렬로 생각할 수 있다. 그렇다면 ${\mathbf{u}}^T$는 $1\times n$의 행렬로 볼 수 있고 행렬곱 ${\mathbf{u}}^T\mathbf{v}$는 $1\times 1$의 행렬이 된다. 그리고 $1\times 1$ 행렬은 스칼라값으로 표시할 수 있다.
이 때, ${\mathbf{u}}^T\mathbf{v}$에 의해 계산된 값을 $\mathbf{u},\mathbf{v}$의 내적(Inner Product, Dot Product)라고 한다. 이는 $\mathbf{u}\cdot \mathbf{v}$로 표기할 수 있다.

Properties of Inner Product

벡터 $\mathbf{u}\mathbf{,}\mathbf{v}\mathbf{,}\mathbf{w}\in {\mathbb{R}}^n$이고 $c$를 스칼라 값이라고 할 때 내적은 다음과 같은 성질을 만족한다.

• $\mathbf{u}\cdot \mathbf{v}=\mathbf{v}\cdot \mathbf{u}$
• $(\mathbf{u}+\mathbf{v})\cdot \mathbf{w}=\mathbf{u}\cdot \mathbf{w}+\mathbf{v}\cdot \mathbf{w}$
• $(c\mathbf{u})\cdot \mathbf{v}=c(\mathbf{u}\cdot \mathbf{v})=\mathbf{u}\cdot (c\mathbf{v})$
• $\mathbf{u}\cdot \mathbf{u}\ge 0$ and $\mathbf{u}\cdot \mathbf{u}=0$ iff $\mathbf{u}=0$

위에서 2,3번 성질을 조합하면 다음과 같은 법칙을 만들 수 있다.
$$\begin{array}{}\text{(26)}& \begin{array}{r}(c_1{\mathbf{u}}_1+\cdots +c_n{\mathbf{u}}_n)\cdot \mathbf{w}=c_1({\mathbf{u}}_1\cdot \mathbf{w})+\cdots +c_n({\mathbf{u}}_n\cdot \mathbf{w})\end{array}\end{array}$$
위를 통해 내적이라는 연산은 선형변환이라는 것을 알 수 있다.

Vector Norm

벡터 $\mathbf{v}\in {\mathbb{R}}^n$에 대해 벡터의 놈(Norm)은 0이 아닌 $\Vert \mathbf{v}\Vert =\sqrt{\mathbf{v}\cdot \mathbf{v}}$로 표기하며 벡터의 길이를 의미한다.
$$\begin{array}{}\text{(27)}& \begin{array}{r}\Vert \mathbf{v}\Vert =\sqrt{\mathbf{v}\cdot \mathbf{v}}=\sqrt{v_1^2+v_2^2+\cdots +v_n^2}\end{array}\end{array}$$
2차원 벡터 $\mathbf{v}\in {\mathbb{R}}^2$가 있을 때 $\mathbf{v}=\left[\begin{array}{c}a\\ b\end{array}\right]$라고 하면 $\Vert v\Vert$는 원점으로부터 $\mathbf{v}$ 좌표까지의 거리가 된다.
$$\begin{array}{}\text{(28)}& \begin{array}{r}\Vert \mathbf{v}\Vert =\sqrt{a^2+b^2}\end{array}\end{array}$$
모든 스칼라 값 $c$에 대해 $c\mathbf{v}$의 길이는 $\mathbf{v}$의 길이를 $|c|$ 배 한 것을 의미한다.
$$\begin{array}{}\text{(29)}& \begin{array}{r}\Vert c\mathbf{v}\Vert =|c|\Vert \mathbf{v}\Vert \end{array}\end{array}$$

Unit Vector

길이가 1인 벡터를 단위벡터(Unit Vector)라고 한다. 벡터의 길이를 1로 맞추는 작업을 정규화(Normalization)라고 하는데 주어진 벡터 $\mathbf{v}$가 있을 때 단위벡터 $\mathbf{u}=\frac{1}{\Vert \mathbf{v}\Vert }\mathbf{v}$가 된다. $\mathbf{u}$ 벡터는 $\mathbf{v}$ 벡터와 방향은 같지만 크기가 1인 벡터이다.

Distance between Vectors in ${\mathbb{R}}^n$

두 벡터 $\mathbf{u}\mathbf{,}\mathbf{v}\in {\mathbb{R}}^n$이 있을 때 두 벡터의 거리는 dist( $\mathbf{u}\mathbf{,}\mathbf{v}$)로 나타내며 이는 $\mathbf{u}\mathbf{-}\mathbf{v}$ 벡터의 길이를 의미한다.
$$\begin{array}{}\text{(30)}& \begin{array}{r}dist(\mathbf{u}\mathbf{,}\mathbf{v})=\Vert \mathbf{u}-\mathbf{v}\Vert \end{array}\end{array}$$

Inner Product and Angle between Vectors

두 벡터 $\mathbf{u}\mathbf{,}\mathbf{v}$의 내적은 다음과 같이 놈과 각도를 통해 표현할 수 있다.
$$\begin{array}{}\text{(31)}& \begin{array}{r}\mathbf{u}\cdot \mathbf{v}=\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert \cos \theta \end{array}\end{array}$$

Orthogonal Vectors

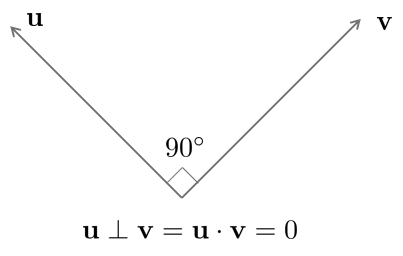
두 벡터 $\mathbf{u}\mathbf{,}\mathbf{v}\in {\mathbb{R}}^n$가 있을 때 둘이 수직이려면 두 벡터의 내적이 0이어야 한다.
$$\begin{array}{}\text{(32)}& \begin{array}{r}\mathbf{u}\cdot \mathbf{v}=\Vert \mathbf{u}\Vert \Vert \mathbf{v}\Vert \cos \theta =0\end{array}\end{array}$$
0이 아닌 두 벡터 $\mathbf{u}\mathbf{,}\mathbf{v}$의 내적이 0이려면 $\cos \theta$ 값이 0이어야 하고 $\theta =90$ degree 일 때 $\cos \theta$ 값은 0이 된다.

Least Square Problem

$\mathbf{A}\in {\mathbb{R}}^{m\times n},\mathbf{b}\in {\mathbb{R}}^n,m\ll n$과 같이 주어진 Overdetermined 시스템 $\mathbf{Ax}=\mathbf{b}$가 있을 때 에러의 제곱합 $\Vert \mathbf{b}-\mathbf{Ax}\Vert$을 최소화하는 최적의 모델 파라미터를 찾는 것이 목적이 된다. 이 때 최소제곱법의 근사해 $\hat{\mathbf{x}}$는 다음과 같다.
$$\begin{array}{}\text{(33)}& \begin{array}{r}\hat{\mathbf{x}}=\arg \underset{\mathbf{x}}{min}\Vert \mathbf{b}-\mathbf{Ax}\Vert \end{array}\end{array}$$

최소제곱법의 중요한 포인트 중 하나는 어떤 $\mathbf{x}$ 파라미터를 선정하던지 벡터 $\mathbf{Ax}$는 반드시 Col $\mathbf{A}$ 안에 위치한다는 것이다. 따라서 최소제곱법은 Col $\mathbf{A}$와 $\mathbf{b}$의 거리가 최소가 되는 $\mathbf{x}$를 찾는 문제가 된다.
$\hat{\mathbf{b}}=\mathbf{A}\hat{\mathbf{x}}$를 만족하는 근사해 $\hat{\mathbf{x}}$는 Col $\mathbf{A}$에서 $\mathbf{b}$ 벡터와 가장 가까운 모든 포인트들의 집합을 의미한다. 따라서 $\mathbf{b}$는 다른 어떤 $\mathbf{Ax}$보다도 $\hat{\mathbf{b}}$와 가장 가깝게 된다. 기하학적으로 이를 만족하기 위해서는 벡터 $\mathbf{b}-\mathbf{A}\hat{\mathbf{x}}$가 Col $\mathbf{A}$와 수직이어야 한다.
$$\begin{array}{}\text{(34)}& \begin{array}{r}\mathbf{b}-\mathbf{A}\hat{\mathbf{x}}\perp (x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\cdots +x_n{\mathbf{a}}_n)\text{for any vector }\mathbf{x}.\end{array}\end{array}$$
이는 곧 다음과 동일하다.
$$\begin{array}{}\text{(35)}& \begin{array}{rl}& (\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})\perp {\mathbf{a}}_1\to {\mathbf{a}}_1^T(\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})\\ & (\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})\perp {\mathbf{a}}_2\to {\mathbf{a}}_2^T(\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})\\ & (\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})\perp {\mathbf{a}}_3\to {\mathbf{a}}_3^T(\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})\\ & \therefore {\mathbf{A}}^T(\mathbf{b}-\mathbf{A}\hat{\mathbf{x}})=0\end{array}\end{array}$$

Normal Equation

$\mathbf{Ax}\simeq \mathbf{b}$를 만족하는 최소제곱법의 근사해는 다음과 같다.
$$\begin{array}{}\text{(36)}& \begin{array}{r}{\mathbf{A}}^T\mathbf{A}\hat{\mathbf{x}}={\mathbf{A}}^T\mathbf{b}\end{array}\end{array}$$
위 식을 정규방정식(Normal Equation) 이라고 부른다. 이는 $\mathbf{C}={\mathbf{A}}^T\mathbf{A}\in {\mathbb{R}}^{n\times n},\mathbf{d}={\mathbf{A}}^T\mathbf{b}\in {\mathbb{R}}^n$일 때 $\mathbf{Cx}=\mathbf{d}$와 같은 선형시스템으로 생각할 수 있다. 이 선형시스템의 해를 구하면 다음과 같다.
$$\begin{array}{}\text{(37)}& \begin{array}{r}\hat{\mathbf{x}}=({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}\end{array}\end{array}$$

Another Derivation of Normal Equation

근사해 $\hat{\mathbf{x}}=\arg \underset{\mathbf{x}}{min}\Vert \mathbf{b}-\mathbf{Ax}\Vert =\arg \underset{\mathbf{x}}{min}\Vert \mathbf{b}-\mathbf{Ax}{\Vert }^2$와 같이 제곱을 최소화하는 문제로 표현해도 동일한 문제가 된다.
$$\begin{array}{}\text{(38)}& \begin{array}{r}\arg \underset{\mathbf{x}}{min}(\mathbf{b}-\mathbf{Ax}{)}^T(\mathbf{b}-\mathbf{Ax})={\mathbf{b}}^T\mathbf{b}-{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{b}-{\mathbf{b}}^T\mathbf{Ax}+{\mathbf{x}}^T{\mathbf{A}}^T\mathbf{Ax}\end{array}\end{array}$$
위 식을 $\mathbf{x}$에 대해서 미분하고 정리하면 다음과 같다.
$$\begin{array}{}\text{(39)}& \begin{array}{r}-{\mathbf{A}}^T\mathbf{b}-{\mathbf{A}}^T\mathbf{b}+2{\mathbf{A}}^T\mathbf{A}\mathbf{x}=0\iff {\mathbf{A}}^T\mathbf{Ax}={\mathbf{A}}^T\mathbf{b}\end{array}\end{array}$$
이 때 ${\mathbf{A}}^T\mathbf{A}$가 역행렬이 존재한다면 다음과 같이 해를 구할 수 있다.
$$\begin{array}{}\text{(40)}& \begin{array}{r}\mathbf{x}=({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}\end{array}\end{array}$$

What If $\mathbf{C}={\mathbf{A}}^T\mathbf{A}$ is NOT Invertible?

행렬 $\mathbf{C}={\mathbf{A}}^T\mathbf{A}$의 역행렬이 존재하지 않는 경우 시스템은 해가 없거나 무수히 많은 해를 가지고 있다. 하지만 정규방정식은 항상 해를 가지고 있으므로 해가 없는 상황은 존재하지 않고 실제로는 무수히 많은 해를 가지고 있다. $\mathbf{C}$가 역행렬을 구할 수 없는 경우는 오직 Col $\mathbf{A}$가 선형의존일 경우에 발생한다. 하지만, 일반적으로 $\mathbf{C}$는 대부분의 경우 역행렬이 존재한다.

Orthogonal Projection Perspective

행렬 $\mathbf{C}={\mathbf{A}}^T\mathbf{A}$가 있을 때 $\mathbf{b}$ 점에서 Col $\mathbf{A}$ 공간으로 프로젝션하면 다음과 같다.
$$\begin{array}{}\text{(41)}& \begin{array}{r}\hat{\mathbf{b}}=f(\mathbf{b})=\mathbf{A}\hat{\mathbf{x}}=\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}\end{array}\end{array}$$

 

Projection Matrix $\mathbf{P}$

위 식에서 $\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T$을 일반적으로 투영 행렬(projection matrix) $\mathbf{P}$라고 한다.

$$\begin{array}{}\text{(42)}& \begin{array}{r}\mathbf{P}=\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\end{array}\end{array}$$

 

투영 행렬은 곱해지는 벡터 $\mathbf{b}$를 열공간(column space) 내에 존재하는 벡터 중 가장 가까운 점 $\hat{\mathbf{b}}$으로 변환해주는 행렬로 생각할 수 있다.

$$\begin{array}{}\text{(43)}& \begin{array}{r}\mathbf{P}\mathbf{b}=\hat{\mathbf{b}}\end{array}\end{array}$$

 

투영 행렬 $\mathbf{P}$의 특징은 다음과 같다.

1. 투영 행렬은 대칭 행렬이다.  $\mathbf{P}={\mathbf{P}}^{⊺}$
2. 투영 행렬은 멱등 행렬(idempotent matrix) $\mathbf{P}={\mathbf{P}}^2$
3. 투영 행렬은 랭크 결핍(rank deficient)이므로 역행렬이 존재하지 않는다.

 

Orthogonal and Orthonormal Sets

벡터들의 집합 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_n\in {\mathbb{R}}^n$가 있을 때 모든 벡터 쌍들이 ${\mathbf{u}}_i\cdot {\mathbf{u}}_j=0,i\ne j$를 만족하면 해당 집합은 직교(Orhogonal) 하다고 말한다.
벡터들의 집합 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_n\in {\mathbb{R}}^n$가 있을 때 모든 직교 집합들이 단위벡터인 경우 정규직교(Orthonormal) 하다고 말한다.
직교벡터와 정규직교벡터의 집합은 항상 선형독립이다.

Orthogonal and Orthonormal Basis

기저벡터 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_n$이 p차원의 부분공간 $W\in {\mathbb{R}}^n$에 있다고 할때 Gram-Schmidt 프로세스와 QR decomposition을 사용하면 직교기저벡터를 만들 수 있다. 부분공간 $W$에 대해 직교기저 벡터 ${\mathbf{u}}_1,\cdots {\mathbf{u}}_n$이 주어져 있다고 했을 때 $\mathbf{y}\in {\mathbb{R}}^n$을 부분공간 $W$ 위로 프로젝션시킨다.

Orthogonal Projection $\hat{\mathbf{y}}$ of $\mathbf{y}$ onto Line

1차원 부분공간 $L=\text{Span}\{\mathbf{u}\}$ 위로 $\mathbf{y}$를 프로젝션하여 $\hat{\mathbf{y}}$를 구하면 다음과 같다.
$$\begin{array}{}\text{(44)}& \begin{array}{r}\hat{\mathbf{y}}={\text{proj}}_L\mathbf{y}=\frac{\mathbf{y}\cdot \mathbf{u}}{\mathbf{u}\cdot \mathbf{u}}\mathbf{u}\end{array}\end{array}$$
가 된다. 만약 $\mathbf{u}$가 단위벡터이면 다음과 같다.
$$\begin{array}{}\text{(45)}& \begin{array}{r}\hat{\mathbf{y}}={\text{proj}}_L\mathbf{y}=(\mathbf{y}\cdot \mathbf{u})\mathbf{u}\end{array}\end{array}$$

Orthogonal Projection $\hat{\mathbf{y}}$ of $\mathbf{y}$ onto Plane

2차원 부분공간 $W=\text{Span}\{{\mathbf{u}}_1,{\mathbf{u}}_2\}$ 위로 $\mathbf{y}$를 프로젝션하여 $\hat{\mathbf{y}}$를 구하면 다음과 같다.
$$\begin{array}{}\text{(46)}& \begin{array}{r}\hat{\mathbf{y}}={\text{proj}}_L\mathbf{y}=\frac{\mathbf{y}\cdot {\mathbf{u}}_1}{{\mathbf{u}}_1{\mathbf{u}}_1}{\mathbf{u}}_1+\frac{\mathbf{y}\cdot {\mathbf{u}}_2}{{\mathbf{u}}_2{\mathbf{u}}_2}{\mathbf{u}}_2\end{array}\end{array}$$
만약 ${\mathbf{u}}_1,{\mathbf{u}}_2$가 단위벡터이면 다음과 같다.
$$\begin{array}{}\text{(47)}& \begin{array}{r}\hat{\mathbf{y}}={\text{proj}}_L\mathbf{y}=(\mathbf{y}\cdot {\mathbf{u}}_1){\mathbf{u}}_1+(\mathbf{y}\cdot {\mathbf{u}}_2){\mathbf{u}}_2\end{array}\end{array}$$
프로젝션은 각각 직교기저벡터에 독립적으로 적용된다.

Orthogonal Projection when $\mathbf{y}\in W$ 

만약 2차원 부분공간 $W=\text{Span}\{{\mathbf{u}}_1,{\mathbf{u}}_2\}$에 $\mathbf{y}$가 포함되어 있다고 하면 프로젝션된 벡터 $\hat{\mathbf{y}}$는 다음과 같이 구할 수 있다.
$$\begin{array}{}\text{(48)}& \begin{array}{r}\hat{\mathbf{y}}={\text{proj}}_L\mathbf{y}=\mathbf{y}=\frac{\mathbf{y}\cdot {\mathbf{u}}_1}{{\mathbf{u}}_1{\mathbf{u}}_1}{\mathbf{u}}_1+\frac{\mathbf{y}\cdot {\mathbf{u}}_2}{{\mathbf{u}}_2{\mathbf{u}}_2}{\mathbf{u}}_2\end{array}\end{array}$$
만약 ${\mathbf{u}}_1,{\mathbf{u}}_2$가 단위벡터이면 다음과 같다.
$$\begin{array}{}\text{(49)}& \begin{array}{r}\hat{\mathbf{y}}={\text{proj}}_L\mathbf{y}=\mathbf{y}=(\mathbf{y}\cdot {\mathbf{u}}_1){\mathbf{u}}_1+(\mathbf{y}\cdot {\mathbf{u}}_2){\mathbf{u}}_2\end{array}\end{array}$$
해는 $\mathbf{y}$가 부분공간 $W$에 포함되어 있지 않은 경우와 동일하다.

Transformation: Orthogonal Projection

부분공간 $W$의 정규직교기저벡터 ${\mathbf{u}}_1,{\mathbf{u}}_2$가 있고 $\mathbf{b}$를 부분공간 $W$에 프로젝션시킨 점 $\hat{\mathbf{b}}$의 변환을 생각해보면
$$\begin{array}{}\text{(50)}& \begin{array}{rl}\hat{\mathbf{b}}& =f(\mathbf{b})=(\mathbf{b}\cdot {\mathbf{u}}_1){\mathbf{u}}_1+(\mathbf{b}\cdot {\mathbf{u}}_2){\mathbf{u}}_2\\ & =({\mathbf{u}}_1^T\mathbf{b}){\mathbf{u}}_1+({\mathbf{u}}_2^T\mathbf{b}){\mathbf{u}}_2\\ & ={\mathbf{u}}_1({\mathbf{u}}_1^T\mathbf{b})+{\mathbf{u}}_2({\mathbf{u}}_2^T\mathbf{b})\\ & =({\mathbf{u}}_1{\mathbf{u}}_1^T)\mathbf{b}+({\mathbf{u}}_2{\mathbf{u}}_2^T)\mathbf{b}\\ & =({\mathbf{u}}_1{\mathbf{u}}_1^T+{\mathbf{u}}_2{\mathbf{u}}_2^T)\mathbf{b}\\ & =[{\mathbf{u}}_1{\mathbf{u}}_2]\left[\begin{array}{c}{\mathbf{u}}_1^T\\ {\mathbf{u}}_2^T\end{array}\right]\mathbf{b}={\mathbf{UU}}^T\mathbf{b}\Rightarrow \text{Linear Transformation!}\end{array}\end{array}$$

 

Orthogonal Projection Perspective

정규직교인 열벡터를 가지는 행렬 $\mathbf{A}=\mathbf{U}=[{\mathbf{u}}_1{\mathbf{u}}_2]$가 있을 때 $\mathbf{b}$ 벡터를 Col $\mathbf{A}$ 공간으로 정사영시키는 경우
$$\begin{array}{}\text{(51)}& \begin{array}{r}\hat{\mathbf{b}}=\mathbf{A}\hat{\mathbf{x}}=\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}=f(\mathbf{b})\end{array}\end{array}$$
행렬 $\mathbf{C}={\mathbf{A}}^T\mathbf{A}$는 $\mathbf{C}=\left[\begin{array}{c}{\mathbf{u}}_1^T\\ {\mathbf{u}}_2^T\end{array}\right]\left[\begin{array}{c}{\mathbf{u}}_1{\mathbf{u}}_2\end{array}\right]=\mathbf{I}$와 같은 성질을 지니게 되고 따라서 다음과 같은 공식이 성립한다.
$$\begin{array}{}\text{(52)}& \begin{array}{r}\hat{\mathbf{b}}=\mathbf{A}\hat{\mathbf{x}}=\mathbf{A}({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{b}=\mathbf{A}(\mathbf{I}{)}^{-1}{\mathbf{A}}^T\mathbf{b}={\mathbf{AA}}^T\mathbf{b}={\mathbf{UU}}^T\mathbf{b}\end{array}\end{array}$$

Gram-Schmidt Orthogonalization

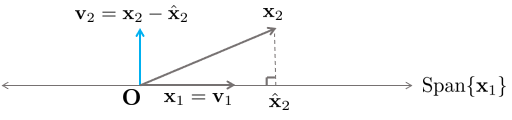
벡터 ${\mathbf{x}}_1=\left[\begin{array}{c}3\\ 6\\ 0\end{array}\right],{\mathbf{x}}_2=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]$로 인해 Span되는 부분공간 $W{x}_1=\text{Span}[{\mathbf{x}}_1,{\mathbf{x}}_2]$가 있을 때 두 벡터의 내적 ${\mathbf{x}}_1\cdot {\mathbf{x}}_2=15\ne 0$이므로 두 벡터는 수직이 아니다.
이 때 벡터 ${\mathbf{v}}_1={\mathbf{x}}_1$이라고 하고 ${\mathbf{v}}_2$를 ${\mathbf{x}}_1$에 수직인 ${\mathbf{x}}_2$의 성분이라고 했을 때
$$\begin{array}{}\text{(53)}& \begin{array}{r}{\mathbf{v}}_2={\mathbf{x}}_2-\frac{{\mathbf{x}}_2\cdot {\mathbf{x}}_1}{{\mathbf{x}}_1\cdot {\mathbf{x}}_1}{\mathbf{x}}_1=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]-\frac{15}{45}\left[\begin{array}{c}3\\ 6\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 2\end{array}\right]\end{array}\end{array}$$
가 된다. 이 때 벡터 ${\mathbf{v}}_1,{\mathbf{v}}_2$는 부분공간 $W$의 직교기저벡터가 된다.

Chapter 3 - Eigenvectors and Eigenvalues

Eigenvectors and Eigenvalues

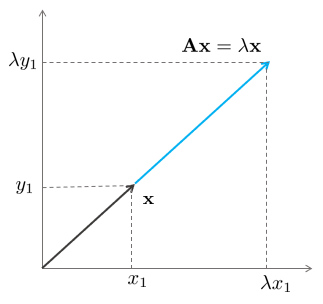
정방행렬 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$에 대한 고유벡터(eigenvector)는 $\mathbf{Ax}=\lambda \mathbf{x}$를 만족하는 0이 아닌 벡터 $\mathbf{x}\in {\mathbb{R}}^n$을 말한다. 이 때 $\lambda$는 행렬 $\mathbf{A}$의 고유값(eigenvalue)이라고 한다.
$\mathbf{Ax}=\lambda \mathbf{x}$는 다음과 같이 다시 나타낼 수 있다.
$$\begin{array}{}\text{(54)}& \begin{array}{r}(\mathbf{A}-\lambda \mathbf{I})\mathbf{x}=0\end{array}\end{array}$$
이 때, 위 시스템이 $\mathbf{x}$가 0이 아닌 비자명해를 가지고 있는 경우에만 $\lambda$ 값이 행렬 $\mathbf{A}$에 대한 고유값이 된다. 위와 같은 동차 선형시스템이 비자명해를 가지기 위해서는 $\mathbf{A}-\lambda \mathbf{I}$가 선형의존(Linearly Dependent)해야 무수히 많은 해를 가진다.

Null Space

행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$의 동차 선형시스템(Homogeneous Linear System) $\mathbf{Ax}=0$의 해 집합을 영공간(Null Space)라고 한다. Nul $\mathbf{A}$로 표기한다.
$\mathbf{A}=\left[\begin{array}{c}{\mathbf{a}}_1^T\\ {\mathbf{a}}_2^T\\ ⋮\\ {\mathbf{a}}_m^T\end{array}\right]$일 때 벡터 $\mathbf{x}$는 다음을 만족해야 한다.
$$\begin{array}{}\text{(55)}& \begin{array}{r}{\mathbf{a}}_1^T\mathbf{x}={\mathbf{a}}_2^T\mathbf{x}=\cdots ={\mathbf{a}}_m^T\mathbf{x}=0\end{array}\end{array}$$
즉, $\mathbf{x}$는 모든 $\mathbf{A}$의 행벡터(Row Vector)과 직교해야 한다.

Orthogonal Complement

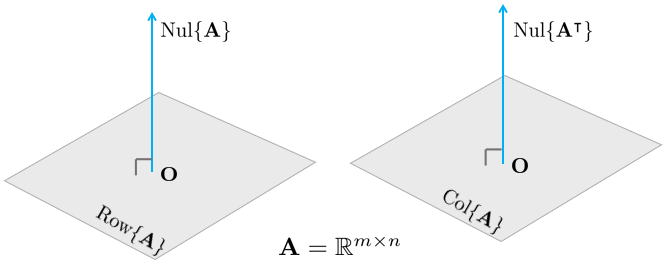
벡터 $\mathbf{z}$가 부분공간 $W\in {\mathbb{R}}^n$의 모든 벡터와 직교하면 $\mathbf{z}$는 부분공간 $W$와 직교한다고 말할 수 있다. 부분공간 $W$와 직교하는 모든 벡터 $\mathbf{z}$의 집합을 직교여공간(Orthogonal Complement)라고 부르며 $W^{\perp }$로 표시한다.
부분공간 $W$의 직교여공간 $W^{\perp }$에 위치한 벡터 $\mathbf{x}\in {\mathbb{R}}^n$는 부분공간 $W$를 Span하는 모든 벡터들과 직교한다.
$$\begin{array}{}\text{(56)}& \begin{array}{rl}& W^{\perp }\text{is a subspace of }{\mathbb{R}}^n.\\ & \text{Nul}\mathbf{A}=(\text{Row}\mathbf{A}{)}^{\perp }\\ & \text{Nul}{\mathbf{A}}^T=(\text{Col}\mathbf{A}{)}^{\perp }\end{array}\end{array}$$

Characteristic Equation

방정식 $(\mathbf{A}-\lambda \mathbf{I})\mathbf{x}=0$이 비자명해를 갖기 위해서는 $(\mathbf{A}-\lambda \mathbf{I})$ 행렬이 선형의존이어야 하고 이는 곧 역행렬이 존재하지 않아야 하는 것과 동치(Equivalent)이다. 만약 $(\mathbf{A}-\lambda \mathbf{I})$이 역행렬이 존재한다면 $\mathbf{x}$는 자명해 이외에는 갖지 못한다.
$$\begin{array}{}\text{(57)}& \begin{array}{rl}& (\mathbf{A}-\lambda \mathbf{I}{)}^{-1}(\mathbf{A}-\lambda \mathbf{I})\mathbf{x}=(\mathbf{A}-\lambda \mathbf{I}{)}^{-1}0\\ & \mathbf{x}=0\end{array}\end{array}$$
따라서 행렬 $\mathbf{A}$에 대하여 고유값과 고유벡터가 존재하기 위해서는 다음의 방정식이 항상 성립해야 한다.
$$\begin{array}{}\text{(58)}& \begin{array}{r}det(\mathbf{A}-\lambda \mathbf{I})=0\end{array}\end{array}$$
위 방정식을 행렬 $\mathbf{A}$의 특성방정식(Characteristic Equation)이라고 부른다.

Eigenspace

$(\mathbf{A}-\lambda \mathbf{x})\mathbf{x}=0$에서 $(\mathbf{A}-\lambda \mathbf{x})$의 영공간(Null Space)를 고유값 $\lambda$에 대한 고유공간(Eigenspace)라고 한다. $\lambda$에 대한 고유공간의 차원이 1 이상인 경우, 고유공간 내에 있는 모든 벡터들에 대하여 다음이 성립한다.
$$\begin{array}{}\text{(59)}& \begin{array}{r}T(\mathbf{x})=\mathbf{Ax}=\lambda \mathbf{x}\end{array}\end{array}$$

Diagonalization

정방행렬 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$이 주어졌고 $\mathbf{V}\in {\mathbb{R}}^{n\times n}$이고 $\mathbf{D}\in {\mathbb{R}}^{n\times n}$일 때
$$\begin{array}{}\text{(60)}& \begin{array}{r}\mathbf{D}={\mathbf{V}}^{-1}\mathbf{AV}\end{array}\end{array}$$
위와 같은 공식이 성립한다면 이를 정방행렬 $\mathbf{A}$의 대각화(Diagonalization)라고 한다. 대각화는 모든 경우에 대해서 항상 가능한 것은 아니다. 행렬 $\mathbf{A}$가 대각화되기 위해서는 역행렬이 존재하는 행렬 $\mathbf{V}$가 존재해야 한다. 행렬 $\mathbf{V}$가 역행렬이 존재하기 위해서는 $\mathbf{V}$는 행렬 $\mathbf{A}$와 같은 ${\mathbb{R}}^{n\times n}$ 크기의 정방행렬이어야 하고 n개의 선형독립인 열벡터를 가지고 있어야 한다. 이 때, $\mathbf{V}$의 각 열은 행렬 $\mathbf{A}$의 고유벡터가 된다. 만약 행렬 $\mathbf{V}$가 존재하는 경우 행렬 $\mathbf{A}$는 대각화 가능(Diangonalizable)하다 고 한다.

Finding $\mathbf{V}$ and $\mathbf{D}$ 

대각화 공식은 다음과 같이 다시 작성할 수 있다.
$$\begin{array}{}\text{(61)}& \begin{array}{r}\mathbf{D}={\mathbf{V}}^{-1}\mathbf{AV}\Rightarrow \mathbf{VD}=\mathbf{AV}\end{array}\end{array}$$
이 때, $\mathbf{V}=\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_n\end{array}\right]$이고 $\mathbf{D}=\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\lambda }_n\end{array}\right]$이라고 하면
$$\begin{array}{}\text{(62)}& \begin{array}{rl}& \mathbf{AV}=\mathbf{A}\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_n\end{array}\right]=\left[\begin{array}{cccc}{\mathbf{Av}}_1& {\mathbf{Av}}_2& \cdots & {\mathbf{Av}}_n\end{array}\right]\\ & \mathbf{VD}=\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_n\end{array}\right]\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\lambda }_n\end{array}\right]\\ & =\left[\begin{array}{cccc}{\lambda }_1{\mathbf{v}}_1& {\lambda }_2{\mathbf{v}}_2& \cdots & {\lambda }_n{\mathbf{v}}_n\end{array}\right]\\ & \mathbf{AV}=\mathbf{VD}\iff \left[\begin{array}{cccc}{\mathbf{Av}}_1& {\mathbf{Av}}_2& \cdots & {\mathbf{Av}}_n\end{array}\right]=\left[\begin{array}{cccc}{\lambda }_1{\mathbf{v}}_1& {\lambda }_2{\mathbf{v}}_2& \cdots & {\lambda }_n{\mathbf{v}}_n\end{array}\right]\end{array}\end{array}$$
위 공식과 같이
$$\begin{array}{}\text{(63)}& \begin{array}{r}{\mathbf{Av}}_1={\lambda }_1{\mathbf{v}}_1,{\mathbf{Av}}_2={\lambda }_2{\mathbf{v}}_2,\cdots ,{\mathbf{Av}}_n={\lambda }_n{\mathbf{v}}_n\end{array}\end{array}$$
각각의 열이 모두 동일해야 한다. 즉, 벡터 ${\mathbf{v}}_i$는 행렬 $\mathbf{A}$에 대한 고유벡터가 되어야 하고 스칼라 ${\lambda }_i$는 행렬 $\mathbf{A}$에 대한 고유값이 되어야 한다. 이에 따라 대각행렬 $\mathbf{D}$는 고유값들을 대각성분으로 포함하고 있는 행렬이 된다. 결론적으로 정방행렬 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$가 대각화 가능한가 안한가에 대한 질문은 n개의 고유벡터가 존재하는가 안하는가에 대한 질문과 동치이다.

Eigendecomposition

정방행렬 $\mathbf{A}$가 대각화 가능한 경우 $\mathbf{D}={\mathbf{V}}^{-1}\mathbf{AV}$ 공식이 성립한다. 이 공식을 다시 작성하면 다음과 같다.
$$\begin{array}{}\text{(64)}& \begin{array}{r}\mathbf{A}={\mathbf{VDV}}^{-1}\end{array}\end{array}$$
이를 행렬 $\mathbf{A}$에 대한 고유값 분해(Eigendecomposition) 라고 한다. 행렬 $\mathbf{A}$가 대각화 가능하다는 의미는 행렬 $\mathbf{A}$가 고유값 분해 가능하다는 말과 동치이다.

Linear Transformation via Eigendecomposition

정방행렬 $\mathbf{A}$가 대각화 가능한 경우 $\mathbf{A}={\mathbf{VDV}}^{-1}$과 같이 고유값 분해가 가능하다. 이 때 선형 변환 $T(\mathbf{x})=\mathbf{Ax}$을 생각해보면 다음과 같이 표현할 수 있다.
$$\begin{array}{}\text{(65)}& \begin{array}{r}T(\mathbf{x})=\mathbf{Ax}={\mathbf{VDV}}^{-1}\mathbf{x}=\mathbf{V}(\mathbf{D}({\mathbf{V}}^{-1}\mathbf{x}))\end{array}\end{array}$$

Change of Basis

예를 들어 ${\mathbf{Av}}_1=-1{\mathbf{v}}_1,{\mathbf{Av}}_2=2{\mathbf{v}}_2$가 성립한다고 가정하고 $T(\mathbf{x})=\mathbf{Ax}={\mathbf{VDV}}^{-1}\mathbf{x}=\mathbf{V}(\mathbf{D}({\mathbf{V}}^{-1}\mathbf{x}))$에서 $\mathbf{y}={\mathbf{V}}^{-1}\mathbf{x}$라고 가정하면
$$\begin{array}{}\text{(66)}& \begin{array}{r}\mathbf{Vy}=\mathbf{x}\end{array}\end{array}$$
의 관계가 성립한다. 이 때, 벡터 $\mathbf{y}$는 벡터 $\mathbf{x}$의 고유벡터 $\{{\mathbf{v}}_1,{\mathbf{v}}_2\}$에 대한 새로운 좌표를 의미한다.
$$\begin{array}{}\text{(67)}& \begin{array}{r}\mathbf{x}=\left[\begin{array}{c}4\\ 3\end{array}\right]=4\left[\begin{array}{c}1\\ 0\end{array}\right]+3\left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}4\\ 3\end{array}\right]=\mathbf{Vy}=[{\mathbf{v}}_1{\mathbf{v}}_2]\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=2{\mathbf{v}}_1+1{\mathbf{v}}_2\Rightarrow \mathbf{y}=\left[\begin{array}{c}2\\ 1\end{array}\right]\end{array}\end{array}$$

Element-wise Scaling

위 과정을 통해 $\mathbf{y}$ 값을 구하고 나면 $T(\mathbf{x})=\mathbf{V}(\mathbf{D}({\mathbf{V}}^{-1}\mathbf{x}))$는 $T(\mathbf{x})=\mathbf{V}(\mathbf{Dy})$로 표현할 수 있다. 이 때 $\mathbf{z}=\mathbf{Dy}$라고 하면 벡터 $\mathbf{z}$는 단순히 벡터 $\mathbf{y}$를 행렬의 대각 원소의 크기만큼 스케일링한 벡터가 된다.

Back to Original Basis

위 과정까지 진행했으면 $T(\mathbf{x})=\mathbf{V}(\mathbf{Dy})=\mathbf{Vz}$와 같이 나타낼 수 있고 이 때 벡터 $\mathbf{z}$는 여전히 새로운 기저벡터 $\{{\mathbf{v}}_1^{{}^{\prime }}{\mathbf{v}}_2^{{}^{\prime }}\}$를 기반으로 하면 좌표가 된다. $\mathbf{Vz}$ 연산은 벡터 $\mathbf{z}$를 다시 원래 기저벡터의 좌표로 변환하는 역할을 한다. 벡터 $\mathbf{Vz}$는 기존의 기저벡터 $\{{\mathbf{v}}_1{\mathbf{v}}_2\}$의 선형결합이 된다.
$$\begin{array}{}\text{(68)}& \begin{array}{r}\mathbf{Vz}=\left[\begin{array}{cc}{\mathbf{v}}_1& {\mathbf{v}}_2\end{array}\right]\left[\begin{array}{c}{z}_1\\ z_2\end{array}\right]={\mathbf{v}}_1{z}_1+{\mathbf{v}}_2{z}_2\end{array}\end{array}$$
지금까지의 과정을 고유값 분해를 통한 선형 변환 이라고 한다.

Linear Transformation via ${\mathbf{A}}^k$ 

여러번의 변환이 중첩된 $\mathbf{A}\times \mathbf{A}\times \cdots \times \mathbf{Ax}={\mathbf{A}}^k\mathbf{x}$를 생각해보자. 이 때, 행렬 $\mathbf{A}$가 대각화 가능하다면 $\mathbf{A}$를 고유값 분해할 수 있고 이 때, ${\mathbf{A}}^k$는 다음과 같이 분해할 수 있다.
$$\begin{array}{}\text{(69)}& \begin{array}{r}{\mathbf{A}}^k=({\mathbf{VDV}}^{-1})({\mathbf{VDV}}^{-1})\cdots ({\mathbf{VDV}}^{-1})={\mathbf{VD}}^k{\mathbf{V}}^{-1}\end{array}\end{array}$$
이 때 ${\mathbf{D}}^k$는 다음과 같이 표현된다.
$$\begin{array}{}\text{(70)}& \begin{array}{r}{\mathbf{D}}^k=\left[\begin{array}{cccc}{\lambda }_1^k& 0& \cdots & 0\\ 0& {\lambda }_2^k& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\lambda }_n^k\end{array}\right]\end{array}\end{array}$$

Geometric Multiplicity and Algebraic Multiplicity

정방행렬 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$이 있을 때 $\mathbf{A}$가 대각화 가능한지 안한지 판단을 해야하는 경우 일반적으로 판별식을 사용하여 판단한다.
$$\begin{array}{}\text{(71)}& \begin{array}{r}det(\mathbf{A}-\lambda \mathbf{I})=0\end{array}\end{array}$$
예를 들어 $n=5$인 정방행렬 $\mathbf{A}$가 있을 때, $det(\mathbf{A}-\lambda \mathbf{I})$는 5차 다항식이 나오게 된다. 5차 다항식은 일반적으로 5개의 해를 가지고 있지만 실수만 고려하는 경우 5개의 해가 계산되지 않을 수 있다. 즉, 실근이 5개가 나오지 않는 경우 $n=5$개의 선형독립인 고유벡터가 나오지 않으므로 대각화가 불가능하다.
만약 실근 중 중근이 포함되는 경우, 예를 들어 $(\lambda -2{)}^2(\lambda -3)=0$과 같이 $\lambda =2$가 중근인 경우, $\lambda =2$로 인해 생성되는 고유공간(Eigenspace)의 차원이 최대 $\lambda =2$가 가지는 중근의 개수까지 가질 수 있다. 중근이 아닌 일반 실근의 경우 최대 1차원의 고유공간을 가질 수 있다. 즉, 중근이 포함된 경우 고유공간의 차원이 최대 $n=5$까지 생성될 수 있는데 $n=5$를 만족하지 못하는 경우에는 대각화가 불가능하다.
이와 같이 대수적으로 판별식을 인수분해했을 때, 중근이 생기는 경우 중근의 대수 중복도(Algebraic Multiplicity) 와 이로 인해 Span되는 고유공간의 기하 중복도(Geometric Multiplicity) 가 일치해야 $n$개의 독립적인 고유벡터가 생성될 수 있고 행렬 $\mathbf{A}$의 대각화가 가능하다.

 

Chapter 4 - Singular Value Decomposition

Singular Value Decomposition

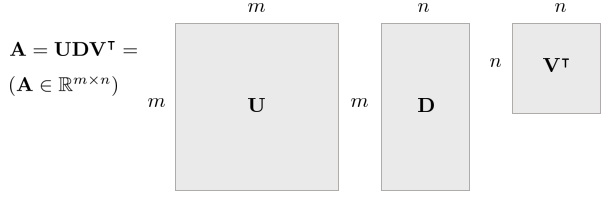
행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$이 주어졌을 때 특이값 분해(Singular Value Decomposition, SVD)는 다음과 같이 나타낼 수 있다.
$$\begin{array}{}\text{(72)}& \begin{array}{r}\mathbf{A}=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T\end{array}\end{array}$$
이 때, $\mathbf{U}\in {\mathbb{R}}^{m\times m},\mathbf{V}\in {\mathbb{R}}^{n\times n}$인 행렬이며 이들은 각 열이 Col $\mathbf{A}$와 Row $\mathbf{A}$에 의 정규직교기저벡터(Orthonormal Basis)로 구성되어 있다. $\mathrm{\Sigma }\in {\mathbb{R}}^{m\times n}$은 대각행렬이며 대각 성분들이 ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_{min(m,n)}$ 특이값이며 큰 값부터 내림차순으로 정렬된 행렬이다.

SVD as Sum of Outer Products

행렬 $\mathbf{A}$는 다음과 같이 외적(Outer Products)의 합으로 표현할 수 있다.
$$\begin{array}{}\text{(73)}& \begin{array}{r}\mathbf{A}=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T=\sum _{i=1}^n{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T,\text{where }{\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_n\end{array}\end{array}$$
이 때 위 식을 다시 행렬로 합성하면 $\mathbf{U}\in {\mathbb{R}}^{m\times m}\to {\mathbf{U}}^{{}^{\prime }}\in {\mathbb{R}}^{m\times n}$ 그리고 $\mathbf{D}\in {\mathbb{R}}^{m\times n}\to {\mathbf{D}}^{{}^{\prime }}\in {\mathbb{R}}^{n\times n}$과 같이 행렬 ${\mathbf{V}}^T$의 차원에 맞게 다시 합성할 수 있는데 이를 Reduced Form of SVD 이라고 한다.
$$\begin{array}{}\text{(74)}& \begin{array}{r}\mathbf{A}={\mathbf{U}}^{{}^{\prime }}{\mathbf{D}}^{{}^{\prime }}{\mathbf{V}}^T\end{array}\end{array}$$

Another Perspective of SVD

행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$에 대해 Gram-Schmidt Orthogonalization을 사용하면 Col $\mathbf{A}$에 대한 정규직교기저벡터 ${\mathbf{u}}_1,\cdots ,{\mathbf{u}}_n$와 Row $\mathbf{A}$에 대한 정규직교기저벡터 ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_n$을 구할 수 있다. 하지만 이렇게 계산한 정규직교기저벡터 ${\mathbf{u}}_i,{\mathbf{v}}_i$는 유일하지 않다.
Reduced Form of SVD를 사용하면 행렬 $\mathbf{U}=\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& \cdots & {\mathbf{u}}_n\end{array}\right]\in {\mathbb{R}}^{m\times n}$과 $\mathbf{V}=\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_n\end{array}\right]\in {\mathbb{R}}^n$ 그리고 $\mathrm{\Sigma }=\left[\begin{array}{cccc}{\sigma }_1& 0& \cdots & 0\\ 0& {\sigma }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\sigma }_n\end{array}\right]\in {\mathbb{R}}^{n\times n}$ 일 때
$$\begin{array}{}\text{(75)}& \begin{array}{rl}& \mathbf{AV}=\mathbf{A}\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& \cdots & {\mathbf{v}}_n\end{array}\right]=\left[\begin{array}{cccc}{\mathbf{Av}}_1& {\mathbf{Av}}_2& \cdots & {\mathbf{Av}}_n\end{array}\right]\\ & \mathbf{U}\mathrm{\Sigma }=\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& \cdots & {\mathbf{u}}_n\end{array}\right]\left[\begin{array}{cccc}{\sigma }_1& 0& \cdots & 0\\ 0& {\sigma }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\sigma }_n\end{array}\right]\\ & \left[\begin{array}{cccc}{\sigma }_1{\mathbf{u}}_1& {\sigma }_2{\mathbf{u}}_2& \cdots & {\sigma }_n{\mathbf{u}}_n\end{array}\right]\\ & \mathbf{AV}=\mathbf{U}\mathrm{\Sigma }\iff \left[\begin{array}{cccc}{\mathbf{Av}}_1& {\mathbf{Av}}_2& \cdots & {\mathbf{Av}}_n\end{array}\right]=\left[\begin{array}{cccc}{\sigma }_1{\mathbf{u}}_1& {\sigma }_2{\mathbf{u}}_2& \cdots & {\sigma }_n{\mathbf{u}}_n\end{array}\right]\end{array}\end{array}$$
위 식을 간결하게 나타내면 다음과 같다.
$$\begin{array}{}\text{(76)}& \begin{array}{r}\mathbf{AV}=\mathbf{U}\mathrm{\Sigma }\iff \mathbf{A}=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T\end{array}\end{array}$$

Computing SVD

행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$에 대하여 ${\mathbf{AA}}^T$와 ${\mathbf{A}}^T\mathbf{A}$는 다음과 같이 고유값분해할 수 있다.
$$\begin{array}{}\text{(77)}& \begin{array}{rl}& {\mathbf{AA}}^T=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T\mathbf{V}{\mathrm{\Sigma }}^T{\mathbf{U}}^T=\mathbf{U}\mathrm{\Sigma }{\mathrm{\Sigma }}^T{\mathbf{U}}^T=\mathbf{U}{\mathrm{\Sigma }}^2{\mathbf{U}}^T\\ & {\mathbf{A}}^T\mathbf{A}=\mathbf{V}{\mathrm{\Sigma }}^T{\mathbf{U}}^T\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T=\mathbf{V}{\mathrm{\Sigma }}^T\mathrm{\Sigma }{\mathbf{U}}^T=\mathbf{V}{\mathrm{\Sigma }}^2{\mathbf{V}}^T\end{array}\end{array}$$
이 때 계산되는 행렬 $\mathbf{U},\mathbf{V}$은 직교하는 고유벡터를 각 열의 성분으로 하는 행렬이며 대각행렬 ${\mathrm{\Sigma }}^2$의 각 성분은 항상 0보다 큰 양수의 값을 가진다. 그리고 ${\mathbf{AA}}^T$와 ${\mathbf{A}}^T\mathbf{A}$를 통해 계산되는 ${\mathrm{\Sigma }}^2$의 값은 동일하다.

Diagonalization of Symmetric Matrices

일반적으로 정방행렬 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$이 $n$개의 선형독립인 고유벡터를 가지고 있을 경우 대각화 가능하다. 그리고 대칭행렬 $\mathbf{S}\in {\mathbb{R}}^{n\times n},{\mathbf{S}}^T=\mathbf{S}$는 항상 대각화 가능하다. 추가적으로 대칭행렬 $\mathbf{S}$의 고유벡터는 항상 서로에게 직교하므로 직교대각화(Orthogonally Diagonalizable)가 가능하다.

Spectral Theorem of Symmetric Matrices

${\mathbf{S}}^T=\mathbf{S}$를 만족하는 대칭행렬 $\mathbf{S}$가 주어졌을 때 $\mathbf{S}$는 $n$개의 중근을 포함한 실수의 고유값이 존재한다. 또한, 고유공간의 차원은 기하 중복도(Algebraic Multiplicity)와 기하 중복도(Geometric Multiplicity)와 같아야 한다. 서로 다른 $\lambda$값 들에 대한 고유공간들은 서로 직교한다. 결론적으로 대칭행렬 $\mathbf{S}$은 직교대각화가 가능하다.

Spectral Decomposition

대칭행렬 $\mathbf{S}$의 고유값 분해는 Spectral Decomposition 이라고 불린다. 이는 다음과 같이 나타낼 수 있다.
$$\begin{array}{}\text{(78)}& \begin{array}{rl}\mathbf{S}& ={\mathbf{UDU}}^{-1}={\mathbf{UDU}}^T=\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& \cdots & {\mathbf{u}}_n\end{array}\right]\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\lambda }_n\end{array}\right]\left[\begin{array}{c}{\mathbf{u}}_1^T\\ {\mathbf{u}}_2^T\\ ⋮\\ {\mathbf{u}}_n^T\end{array}\right]\\ & =\left[\begin{array}{cccc}{\lambda }_1{\mathbf{u}}_1& {\lambda }_2{\mathbf{u}}_2& \cdots & {\lambda }_n{\mathbf{u}}_n\end{array}\right]\left[\begin{array}{c}{\mathbf{u}}_1^T\\ {\mathbf{u}}_2^T\\ ⋮\\ {\mathbf{u}}_n^T\end{array}\right]\\ & ={\lambda }_1{\mathbf{u}}_1{\mathbf{u}}_1^T+{\lambda }_2{\mathbf{u}}_2{\mathbf{u}}_2^T+\cdots +{\lambda }_n{\mathbf{u}}_n{\mathbf{u}}_n^T\end{array}\end{array}$$
위 식에서 각 항 ${\lambda }_i{\mathbf{u}}_j{\mathbf{u}}_j^T$은 ${\mathbf{u}}_j$에 의해 Span된 부분공간에 프로젝션된 다음 고유값 ${\lambda }_i$만큼 스케일된 벡터로 볼 수 있다.
 

Symmetric Positive Definite Matrices

행렬 $\mathbf{S}\in {\mathbb{R}}^{n\times n}$이 대칭이면서 Positive Definite인 경우 Spectral Decomposition의 모든 고유값은 항상 양수가 된다.
$$\begin{array}{}\text{(79)}& \begin{array}{rl}\mathbf{S}& ={\mathbf{UDU}}^{-1}={\mathbf{UDU}}^T=\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& \cdots & {\mathbf{u}}_n\end{array}\right]\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& {\lambda }_n\end{array}\right]\left[\begin{array}{c}{\mathbf{u}}_1^T\\ {\mathbf{u}}_2^T\\ ⋮\\ {\mathbf{u}}_n^T\end{array}\right]\\ & ={\lambda }_1{\mathbf{u}}_1{\mathbf{u}}_1^T+{\lambda }_2{\mathbf{u}}_2{\mathbf{u}}_2^T+\cdots +{\lambda }_n{\mathbf{u}}_n{\mathbf{u}}_n^T\\ & \text{where, }{\lambda }_j>0,\mathrm{\forall }j=1,\cdots ,n\end{array}\end{array}$$

Back to Computing SVD

행렬 $\mathbf{A}$에 대하여 ${\mathbf{AA}}^T={\mathbf{A}}^T\mathbf{A}=\mathbf{S}$인 대칭행렬이 존재할 때 $\mathbf{S}$가 Positive (Semi-)Definite한 경우
$$\begin{array}{}\text{(80)}& \begin{array}{rl}& {\mathbf{x}}^T{\mathbf{AA}}^T\mathbf{x}=({\mathbf{A}}^T\mathbf{x}{)}^T({\mathbf{A}}^T\mathbf{x})=\Vert {\mathbf{A}}^T\mathbf{x}\Vert \ge 0\\ & {\mathbf{x}}^T{\mathbf{A}}^T\mathbf{Ax}=(\mathbf{Ax}{)}^T(\mathbf{Ax})=\Vert \mathbf{Ax}{\Vert }^2\ge 0\end{array}\end{array}$$
즉, ${\mathbf{AA}}^T=\mathbf{U}{\mathrm{\Sigma }}^2{\mathbf{U}}^T$와 ${\mathbf{A}}^T\mathbf{A}=\mathbf{V}{\mathrm{\Sigma }}^2{\mathbf{V}}^T$에서 ${\mathrm{\Sigma }}^2$의 값은 항상 양수가 된다.
임의의 직각 행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$에 대하여 특이값 분해는 언제나 존재한다. $\mathbf{A}\in {\mathbb{R}}^{n\times n}$ 행렬의 경우 고유값 분해가 존재하지 않을 수 있지만 특이값 분해는 항상 존재한다. 대칭이면서 동시에 Positive Definite인 정방 행렬 $\mathbf{S}\in {\mathbb{R}}^{n\times n}$은 항상 고유값 분해값이 존재하며 이는 특이값 분해와 동일하다.

Eigendecomposition in Machine Learning

일반적으로 기계학습에서는 대칭이고 Positive Definite인 행렬을 다룬다. 예를 들면, $\mathbf{A}\in {\mathbb{R}}^{10\times 3}$인 행렬이 있고 각 열은 사람을 의미하고 각 행은 Feature를 의미한다고 가정했을 때, ${\mathbf{A}}^T\mathbf{A}\in {\mathbb{R}}^{3\times 3}$는 각 사람들 간 유사도 를 의미하고 ${\mathbf{AA}}^T\in {\mathbb{R}}^{10\times 10}$는 각 Feature들의 상관관계를 의미한다. 이 때, ${\mathbf{AA}}^T$는 주성분분석(Principal Component Analysis)에서 Covariance Matrix를 구할 때 사용된다.

Low Rank Approximation of a Matrix

행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$이 주어졌을 때 예를 들어, $\mathbf{A}$의 원래 rank가 r일 때, 행렬 $\mathbf{A}$에서 rank를 r 이하를 가진 근사행렬 $\hat{\mathbf{A}}$을 찾는 Low Rank Approximation을 수행할 수 있다.
$$\begin{array}{}\text{(81)}& \begin{array}{rl}& {\hat{\mathbf{A}}}_r=\arg \underset{{\hat{\mathbf{A}}}_r}{min}\Vert \mathbf{A}-{\mathbf{A}}_r{\Vert }_F,\text{subject to rank}{\mathbf{A}}_r\le r\\ & {\hat{\mathbf{A}}}_r=\sum _{i=1}^r{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T\text{where, }{\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_r\end{array}\end{array}$$

Dimension Reducing Transformation

Feature-by-data item 행렬 $\mathbf{A}\in {\mathbb{R}}^{m\times n}$이 주어졌을 때 $\mathbf{G}\in {\mathbb{R}}^{m\times r},r<m$인 변환 ${\mathbf{G}}^T:\mathbf{x}\in {\mathbb{R}}^m\mapsto \mathbf{y}\in {\mathbb{R}}^r$을 생각해보면
$$\begin{array}{}\text{(82)}& \begin{array}{r}{\mathbf{y}}_i={\mathbf{G}}^T{\mathbf{a}}_i\end{array}\end{array}$$
가 성립하고 $\mathbf{G}$ 의 각 열들은 정규직교벡터이며 데이터의 유사도 행렬 $\mathbf{S}={\mathbf{A}}^T\mathbf{A}$의 유사도를 보존하는 변환 $\mathbf{G}$를 차원 축소 변환(Dimension-Reducing Transformation) 이라고 한다.
$$\begin{array}{}\text{(83)}& \begin{array}{rl}& \mathbf{Y}={\mathbf{G}}^T\mathbf{A}\\ & {\mathbf{Y}}^T\mathbf{Y}=({\mathbf{G}}^T\mathbf{A}{)}^T{\mathbf{G}}^T\mathbf{A}={\mathbf{A}}^T{\mathbf{GG}}^T\mathbf{A}\end{array}\end{array}$$
이 때 차원축소변환 $\hat{\mathbf{G}}$ 은 다음과 같이 추정할 수 있다.
$$\begin{array}{}\text{(84)}& \begin{array}{r}\hat{\mathbf{G}}=\arg \underset{\mathbf{G}}{min}\Vert S-{\mathbf{A}}^T{\mathbf{GG}}^T\mathbf{A}{\Vert }_F\text{subject to }{\mathbf{G}}^T\mathbf{G}={\mathbf{I}}_k\end{array}\end{array}$$
주어진 행렬 $\mathbf{A}=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T=\sum _{i=1}^n{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T$에 대하여 최적의 해는 다음과 같다.
$$\begin{array}{}\text{(85)}& \begin{array}{r}\hat{\mathbf{G}}={\mathbf{U}}_r=\left[\begin{array}{cccc}{\mathbf{u}}_1& {\mathbf{u}}_2& \cdots & {\mathbf{u}}_r\end{array}\right]\end{array}\end{array}$$
 

Chapter 5 - Derivative of multi-variable function

Gradient

임의의 벡터 $\mathbf{x}\in {\mathbb{R}}^n$에 대하여 $f(\mathbf{x})\in \mathbb{R}$를 만족하는 다변수 스칼라 함수 $f(\mathbf{x})$가 주어졌다고 하자. 
$$\begin{array}{}\text{(86)}& \begin{array}{r}f:{\mathbb{R}}^n\mapsto \mathbb{R}\end{array}\end{array}$$ 

$f(\mathbf{x})$에 대한 1차 편미분은 벡터가 되고 이는 그레디언트(gradient)라고 불린다.
$$\begin{array}{}\text{(87)}& \boxed{{\displaystyle \begin{array}{r}\mathrm{\nabla }\mathbf{f}=\left(\begin{array}{ccc}\frac{\partial f}{\partial x_1}& \cdots & \frac{\partial f}{\partial x_n}\end{array}\right)\in {\mathbb{R}}^{1\times n}\end{array}}}\end{array}$$

Jacobian matrix

임의의 벡터 $\mathbf{x}\in {\mathbb{R}}^n$에 대하여 $f(\mathbf{x})\in {\mathbb{R}}^m$를 만족하는 다변수 벡터 함수 $f(\mathbf{x})$가 주어졌다고 하자. 
$$\begin{array}{}\text{(88)}& \begin{array}{r}f:{\mathbb{R}}^n\mapsto {\mathbb{R}}^m\end{array}\end{array}$$ 

이 때, $f(\cdot )$의 1차 편미분은 행렬이 되고 이를 특별히 자코비안(jacobian) 행렬이라고 한다.
$$\begin{array}{}\text{(89)}& \boxed{{\displaystyle \begin{array}{r}\mathbf{J}=\left[\begin{array}{ccc}\frac{\partial f_1}{\partial x_1}& \cdots & \frac{\partial f_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial f_m}{\partial x_1}& \cdots & \frac{\partial f_m}{\partial x_n}\end{array}\right]\in {\mathbb{R}}^{m\times n}\end{array}}}\end{array}$$ 

이를 통해 자코비안 행렬의 각 행벡터(row vector)는 함수 $f_m(\cdot )$에 대한 그레디언트라는 것을 알 수 있다.
. 위 식을 미소변화량 $\mathbf{h}$를 사용하여 나타내면 다음과 같다.
$$\begin{array}{}\text{(90)}& \begin{array}{r}\mathbf{J}=\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}}\triangleq \underset{\mathbf{h}\to \mathbf{0}}{lim}\frac{f(\mathbf{x}+\mathbf{h})-f(\mathbf{x})}{\mathbf{h}}\in {\mathbb{R}}^{m\times n}\end{array}\end{array}$$ 

 

SLAM에서 자코비안은 에러 $\mathbf{e}(\mathbf{x})$를 최적화할 때 사용된다. SLAM에서 최적화하고자 하는 에러는 일반적으로 비선형 함수로 구성되어 있으며 크기가 작기 때문에 에러의 변화량 $\mathbf{e}(\mathbf{x}+\mathrm{\Delta }\mathbf{x})$를 그대로 사용하지 않고 테일러 전개하여 근사식 $\mathbf{e}(\mathbf{x})+\mathbf{J}\mathrm{\Delta }\mathbf{x}$으로 표현하게 되는데 이 때 에러에 대한 자코비안 $\mathbf{J}$가 유도된다. 그리고 근사식을 바탕으로 유도한 에러의 최적 증분량 $\mathrm{\Delta }{\mathbf{x}}^{\ast }=({\mathbf{J}}^{⊺}\mathbf{J}{)}^{-1}{\mathbf{J}}^{⊺}\mathbf{b}$이 자코비안을 통해 구해지기 때문에 SLAM에서는 자코비안이 필수적으로 사용된다. 자세한 내용은 https://alida.tistory.com/65#sec2  포스트를 참조하면 된다.

 

Toy example 1

만약 $\mathbf{x}=\{a,b,c\}$일 때 $f(\mathbf{x})=f(a,b,c)$를 각각의 변수 a,b,c에 대해 편미분하면 다음과 같다.

$$\begin{array}{}\text{(91)}& \begin{array}{rl}& \mathbf{J}=\frac{\partial f(\mathbf{x})}{\partial \mathbf{x}}=\left[\begin{array}{ccc}{\mathbf{J}}_a& {\mathbf{J}}_b& {\mathbf{J}}_c\end{array}\right]\end{array}\end{array}$$

$$\begin{array}{}\text{(92)}& \begin{array}{rl}& {\mathbf{J}}_a=\frac{\partial f(a,b,c)}{\partial a}\\ & {\mathbf{J}}_b=\frac{\partial f(a,b,c)}{\partial b}\\ & {\mathbf{J}}_c=\frac{\partial f(a,b,c)}{\partial c}\end{array}\end{array}$$

 

만약 $a=a_0$로 계산값(=operating point)이 정해진 경우 자코비안은 다음과 같다.

$$\begin{array}{}\text{(93)}& \begin{array}{rl}& {\mathbf{J}}_a=\frac{\partial f(a,b,c)}{\partial a}{|}_{a=a_0}\\ & {\mathbf{J}}_b=\frac{\partial f(a,b,c)}{\partial b}{|}_{a=a_0,b=b_0}\\ & {\mathbf{J}}_c=\frac{\partial f(a,b,c)}{\partial c}{|}_{a=a_0,c=c_0}\end{array}\end{array}$$

 

위 첫번째 식은 $f(a,b,c)$를 $a$에 대해 편미분한 후 $a=a_0$를 넣어 값을 계산하라는 의미이고 두번째와 세번째 식은 $a=a_0$로 값을 고정한 상태에서 각각 $b=b_0,c=c_0$에 대한 편미분을 수행하라는 의미이다.

Toy example 2
예를 들어 다음과 같은 3개의 연립 방정식이 주어졌다고 하자. 
$$\begin{array}{}\text{(94)}& \begin{array}{r}f(\mathbf{x})=\{\begin{array}{l}{f}_1(\mathbf{x})=a{x}^2+2bx+cy\\ f_2(\mathbf{x})=d{x}^3+ex\\ f_3(\mathbf{x})=fx+g{y}^2+hy\end{array}\end{array}\end{array}$$

$\mathbf{x}=(x,y)$를 의미한다. 위 함수는 다음과 같이 쓸 수 있다.
$$\begin{array}{}\text{(95)}& \begin{array}{r}f:{\mathbb{R}}^2\mapsto {\mathbb{R}}^3\end{array}\end{array}$$ 

자코비안의 정의에 따라 이를 아래와 같이 쓸 수 있다.
$$\begin{array}{}\text{(96)}& \begin{array}{r}\mathbf{J}=\left[\begin{array}{cc}\frac{\partial f_1}{\partial x}& \frac{\partial f_1}{\partial y}\\ \frac{\partial f_2}{\partial x}& \frac{\partial f_2}{\partial y}\\ \frac{\partial f_3}{\partial x}& \frac{\partial f_3}{\partial y}\end{array}\right]=\left[\begin{array}{cc}2ax+2b& c\\ 3d{x}^2+e& 0\\ f& 2gy+h\end{array}\right]\in {\mathbb{R}}^{3\times 2}\end{array}\end{array}$$

Hessian matrix

임의의 벡터 $\mathbf{x}\in {\mathbb{R}}^n$에 대하여 $f(\mathbf{x})\in \mathbb{R}$를 만족하는 다변수 스칼라 함수 $f(\mathbf{x})$가 주어졌다고 하자. 
$$\begin{array}{}\text{(97)}& \begin{array}{r}f:{\mathbb{R}}^n\mapsto \mathbb{R}\end{array}\end{array}$$ 

이 때, $f(\cdot )$의 2차 편미분은 행렬이 되고 이를 특별히 헤시안(hessian) 행렬이라고 한다. 헤시안 행렬은 일반적으로 대칭행렬의 형태를 띄고 있으며 다변수 벡터 함수가 아닌 다변수 스칼라 함수에 대한 2차 미분임에 유의한다. 
$$\begin{array}{}\text{(98)}& \boxed{{\displaystyle \begin{array}{r}\mathbf{H}=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1{x}_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1{x}_n}\\ \frac{{\partial }^{2}f}{\partial x_2{x}_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2{x}_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n{x}_1}& \frac{{\partial }^{2}f}{\partial x_n{x}_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]\in {\mathbb{R}}^{n\times n}\end{array}}}\end{array}$$ 

 

헤시안 행렬 $\mathbf{H}$는 자코비안 $\mathbf{J}$의 미분 행렬이 아님에 유의한다. 자코비안 $\mathbf{J}$는 다변수 벡터 함수에 대한 1차 미분 행렬을 의미하는데 반해 헤시안 행렬 $\mathbf{H}$는 다변수 스칼라 함수의 2차 미분 행렬을 의미한다. 다변수 스칼라 함수의 1차 미분은 그라디언트 $\mathrm{\nabla }\mathbf{f}$ 벡터이다.  일반적으로 다변수 벡터 함수의 2차 미분은 정의되지 않는다.
$$\begin{array}{}\text{(99)}& \boxed{{\displaystyle \begin{array}{rl}& f:{\mathbb{R}}^n\mapsto \mathbb{R}\text{then,}\\ & f^{\prime }:\mathrm{\nabla }\mathbf{f}\cdots \text{gradient}\\ & f^{″}:\mathbf{H}\cdots \text{hessian}\end{array}}}\end{array}$$
$$\begin{array}{}\text{(100)}& \boxed{{\displaystyle \begin{array}{rl}& f:{\mathbb{R}}^n\mapsto {\mathbb{R}}^m\text{then,}\\ & f^{\prime }:\mathbf{J}\cdots \text{jacobian}\end{array}}}\end{array}$$

Laplacian

임의의 벡터 $\mathbf{x}\in {\mathbb{R}}^n$에 대하여 $f(\mathbf{x})\in \mathbb{R}$를 만족하는 다변수 스칼라 함수 $f(\mathbf{x})$가 주어졌다고 하자. 
$$\begin{array}{}\text{(101)}& \begin{array}{r}f:{\mathbb{R}}^n\mapsto \mathbb{R}\end{array}\end{array}$$ 

$f(\mathbf{x})$에 대한 라플라시안(laplacian)은 각 입력 벡터에 따른 2차 편미분의 합으로 정의된다.
$$\begin{array}{}\text{(102)}& \boxed{{\displaystyle \begin{array}{r}{\mathrm{\nabla }}^2\mathbf{f}=\frac{{\partial }^{2}f}{\partial x_1^2}+\frac{{\partial }^{2}f}{\partial x_2^2}+\cdots +\frac{{\partial }^{2}f}{\partial x_n^2}\in {\mathbb{R}}^{1\times n}\end{array}}}\end{array}$$

Taylor expansion

테일러 전개(expansion)은 미지의 함수 $f(x)$를 $x=a$ 지점에서 근사 다항함수로 표현하는 방법을 말한다. 이는 테일러 급수(series) 또는 테일러 근사(approximation)이라고도 불린다. $f(\cdot )$을 $x=a$ 부근에서 테일러 전개를 수행하면 다음과 같이 나타낼 수 있다.
$$\begin{array}{}\text{(103)}& \begin{array}{r}{f(x)|}_{x=a}=f(a)+f^{\prime }(a)(x-a)+\frac{1}{2!}{f}^{″}(a)(x-a{)}^2+\frac{1}{3!}{f}^{‴}(a)(x-a{)}^3+\cdots \end{array}\end{array}$$

함수 $f(\cdot )$가 다변수 스칼라 함수일 경우 $\mathbf{x}=\mathbf{a}$ 지점에서 테일러 전개는 다음과 같이 쓸 수 있다. 
$$\begin{array}{}\text{(104)}& \begin{array}{r}{f(\mathbf{x})|}_{\mathbf{x}=\mathbf{a}}=f(\mathbf{a})+\mathrm{\nabla }\mathbf{f}(\mathbf{x}-\mathbf{a})+\frac{1}{2!}(\mathbf{x}-\mathbf{a}{)}^{⊺}\mathbf{H}(\mathbf{x}-\mathbf{a})+\cdots \end{array}\end{array}$$

이 때, $\mathrm{\nabla }\mathbf{f}$는 함수 $f(\cdot )$의 그레디언트(gradient) 의미하며 $\mathbf{H}$는 헤시안(hessian) 행렬을 의마한다.
 

References

[1] (Lecture) 인공지능을 위한 선형대수 - 주재걸 교수님 (edwith)

[2] (Book) Kay, Steven M. Fundamentals of statistical signal processing: estimation theory. Prentice-Hall, Inc., 1993.
[3] (Blog) 다크프로그래머 - Gradient, Jacobian 행렬, Hessian 행렬, Laplacian
[4] (Blog) [행렬대수학] 행렬식(Determinant) 1 - 행렬식의 개념

[6] (Pdf) Pseudo Inverse 유도 과정
[7] (Youtube) Matrix Inversion Lemma 강의 영상 - 혁펜하임