[SLAM] Direct Sparse Odometry (DSO) 논문 및 코드 리뷰 (2)

4. Keyframes

4.1. Inverse Depth Update

To be added

4.2. Immature Point Activation

To be added

4.3. Sliding Window Optimization

4.3.1. Error Function Formulation

특정 프레임이 키프레임으로 결정되면 sliding window 내부의 키프레임들과 새로운 키프레임 사이에 에러함수를 업데이트해야 한다. 이 때, 키프레임 뿐만 아니라 이와 연결되어 있는 맵 상의 포인트들까지 같이 최적화하는 Local Bundle Adjustment (LBA)를 수행한다.

 

주목할 점은 하나의 맵포인트가 두 개의 키프레임(host, target)과 연결되어 최적화된다는 점이다. 여기서 host 키프레임은 해당 맵포인트를 가장 먼저 발견한 키프레임이고 target 키프레임은 이후에 발견한 키프레임을 의미한다.

또한 최적화 과정에서 연산량을 줄이기 위해 Jacobian을 계산할 때 카메라의 월드좌표계를 기준으로 계산한 Jacobian $\frac{\partial \mathbf{r}}{\partial {\xi }_{wh}},\frac{\partial \mathbf{r}}{\partial {\xi }_{wt}}$을 사용하지 않고 host, target 키프레임 간 상대 포즈를 기준으로 계산한 Jacobian $\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}$를 사용한다. 따라서 해당 Jacobian을 사용하여 두 키프레임의 월드좌표계 기반 카메라 포즈 ${\mathbf{T}}_{wh},{\mathbf{T}}_{wt}$를 최적화하기 위해 Adjoint Transformationd르 사용한다. (추후 섹션에서 설명)

sliding window optimization을 수행하기 위해 우선 에러함수를 설정해야 한다. 이 때, 에러함수의 파라미터는 pose(6) + photometric(2) + camera intrinsic(4) + idepth(N)로써 총 12+N개의 파라미터가 최적화에 사용된다. 참고로 Initialization 과정에서는 camera intrinsic(4)를 제외한 8+N개의 파라미터가 최적화되었다. 즉, camera intrinsic ($(f_x,f_y,c_x,c_y)$)를 제외하고 Jacobian은 이전과 동일하다.

 

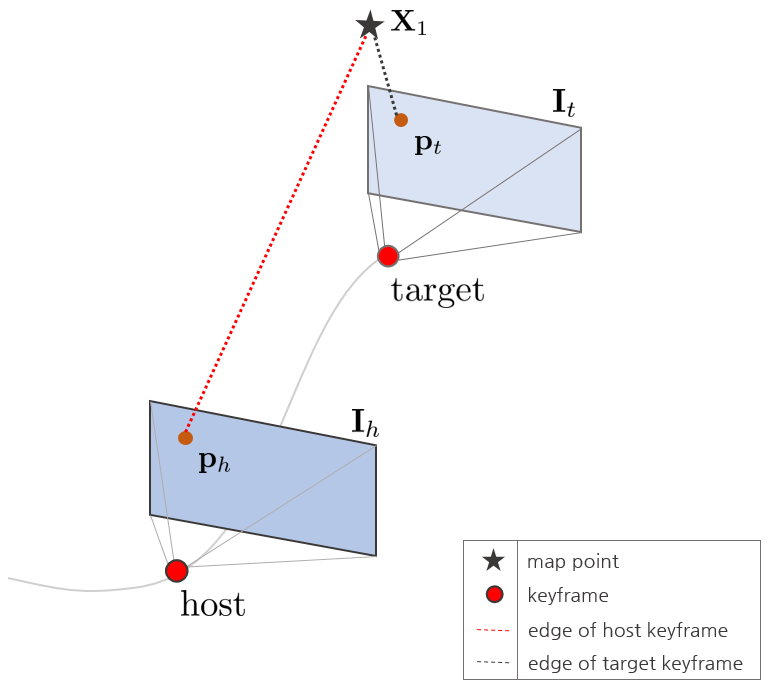
에러(residual)은 다음과 같이 설정할 수 있다.

$$\mathbf{r}={\mathbf{I}}_t({\mathbf{p}}_t)-\exp (a)({\mathbf{I}}_h({\mathbf{p}}_h)-b_0)-b$$

- ${\mathbf{p}}_t=\pi (\exp ({\xi }_{th}^{\wedge }){\mathbf{X}}_1)=\pi (\exp ({\xi }_{th}^{\wedge }){\pi }^{-1}({\mathbf{p}}_h))$

 

이 때, residual은 한 점이 아닌 8-point patch 점들의 에러 합을 의미한다. 최종적으로 huber norm까지 적용된 에러함수는 다음과 같다. 

$$\text{H}(\mathbf{r})=w_h{\mathbf{r}}^2$$

 

해당 에러함수가 최소가 되는 파라미터를 찾기 위해 $f(\mathbf{x}{)}^{T}f(\mathbf{x})=\text{H}(\mathbf{r})$를 만족하는 $f(\mathbf{x})$를 최소화하는 문제로 변경하면 다음과 같다. 

$$f(\mathbf{x})=\sqrt{w_h}\mathbf{r}=\sqrt{w_h}({\mathbf{I}}_2({\mathbf{p}}_2)-\exp (a)({\mathbf{I}}_1({\mathbf{p}}_1-b_0))-b)$$

 

에러함수 $f(\mathbf{x})$에 state variable $\mathbf{x}$은 다음과 같다

$$f(\mathbf{x})=\sqrt{w_h}\mathbf{r}=\sqrt{w_h}({\mathbf{I}}_t({\mathbf{p}}_t)-\exp (a)({\mathbf{I}}_h({\mathbf{p}}_h-b_0))-b)$$

$$\mathbf{x}=[{\rho }_1^{(1)},\cdots ,{\rho }_1^{(N)},\delta {\xi }^T,a,b,\mathbf{c}{]}_{(N+12)\times 1}^T$$

 

- ${\rho }_1^{(i)}$ : 1번 이미지에서 i번째 inverse depth 값 (N개)

- $\delta \xi$ : 두 카메라 간 상대 포즈 변화량 (twist) (6차원 벡터) (6개)

- $a,b$ : 두 이미지 간 exposure time을 고려하여 이미지 밝기를 조절하는 파라미터 (2개)

- $\mathbf{c}$ : 카메라 내부 파라미터 (fx,fy,cx,cy) (4개)

 

Initialization 과정과 달리 에러함수 $\mathbf{x}$에 camera intrinsic $\mathbf{c}$가 포함된 것을 알 수 있다. Initialization 과정에서 이미 아래와 같이 최적화에 필요한 Jacobian들을 유도하였다. 

idepth(N)

$$\frac{\partial f(\mathbf{x})}{\partial {\rho }_1}=\sqrt{w_h}{\rho }_1^{-1}{\rho }_2(\mathrm{\nabla }{\mathbf{I}}_x{f}_x(t_x-u_2^{{}^{\prime }}{t}_z)+\mathrm{\nabla }{\mathbf{I}}_y{f}_y(t_y-v_2^{{}^{\prime }}{t}_z))$$

pose(6)

$$\frac{\partial f(\mathbf{x})}{\partial \delta \xi }=\sqrt{w_h}{\left[\begin{array}{c}\mathrm{\nabla }{\mathbf{I}}_x{\rho }_2{f}_x\\ \mathrm{\nabla }{\mathbf{I}}_y{\rho }_2{f}_y\\ -{\rho }_2(\mathrm{\nabla }{\mathbf{I}}_x{f}_x{u}_2^{{}^{\prime }}+\mathrm{\nabla }{\mathbf{I}}_y{f}_y{v}_2^{{}^{\prime }})\\ -\mathrm{\nabla }{\mathbf{I}}_x{f}_x{u}_2^{{}^{\prime }}{v}_2^{{}^{\prime }}-\mathrm{\nabla }{\mathbf{I}}_y{f}_y(1+v_2^{{}^{\prime }2})\\ \mathrm{\nabla }{\mathbf{I}}_x{f}_x(1+u_2^{{}^{\prime }2})+\mathrm{\nabla }{\mathbf{I}}_y{f}_y{u}_2^{{}^{\prime }}{v}_2^{{}^{\prime }}\\ -\mathrm{\nabla }{\mathbf{I}}_x{f}_x{v}_2^{{}^{\prime }}+\mathrm{\nabla }{\mathbf{I}}_y{f}_y{u}_2^{{}^{\prime }}\end{array}\right]}^T$$

photometric(2)

$$\frac{\partial f(\mathbf{x})}{\partial a}=-\sqrt{w_h}\exp (a){\mathbf{I}}_1({\mathbf{p}}_1)$$

$$\frac{\partial f(\mathbf{x})}{\partial b}=-\sqrt{w_h}$$

 

하지만 sliding window optimization 과정에서는 추가적으로 Jacobian of Camera Intrinsic 

$\frac{\partial f(\mathbf{x})}{\partial \mathbf{c}}$을 유도해야 한다.

 

4.3.2. Derivate Jacobian of Camera Intrinsics

$\frac{\partial f(\mathbf{x})}{\partial \mathbf{c}}$는 다음과 같이 분해할 수 있다. 

$$\frac{\partial f(\mathbf{x})}{\partial \mathbf{c}}=\frac{\partial f(\mathbf{x})}{\partial {\mathbf{p}}_t}\frac{\partial {\mathbf{p}}_t}{\partial \mathbf{c}}$$

 

이 때, $f(\mathbf{x})=\sqrt{w_h}\mathbf{r}$이므로 간결하게 residual 항으로 표현하면 다음과 같다. 

$$\frac{\partial \mathbf{r}}{\partial \mathbf{c}}=\frac{\partial \mathbf{r}}{\partial {\mathbf{p}}_t}\frac{\partial {\mathbf{p}}_t}{\partial \mathbf{c}}$$

 

$\frac{\partial \mathbf{r}}{\partial {\mathbf{p}}_t}$는 Initialization 섹션에서 다음과 같이 이미 유도하였다. 

$$\frac{\partial \mathbf{r}}{\partial {\mathbf{p}}_t}=\frac{\partial {\mathbf{I}}_{\mathbf{t}}({\mathbf{p}}_{\mathbf{t}})}{\partial {\mathbf{p}}_t}=[\mathrm{\nabla }{\mathbf{I}}_x\mathrm{\nabla }{\mathbf{I}}_y]$$

 

그리고 $\frac{\partial {\mathbf{p}}_t}{\partial \mathbf{c}}$는 다음과 같이 유도할 수 있다.  

$$\begin{array}{rl}\frac{\partial {\mathbf{p}}_t}{\partial \mathbf{c}}& =\left[\begin{array}{cccc}\frac{\partial u_t}{\partial f_x}& \frac{\partial u_t}{\partial f_y}& \frac{\partial u_t}{\partial c_x}& \frac{\partial u_t}{\partial c_y}\\ \frac{\partial v_t}{\partial f_x}& \frac{\partial v_t}{\partial f_y}& \frac{\partial v_t}{\partial c_x}& \frac{\partial v_t}{\partial c_y}\end{array}\right]\\ & =\left[\begin{array}{cccc}{\overline{u}}_t+f_x\frac{\partial {\overline{u}}_t}{\partial f_x}& f_x\frac{\partial {\overline{u}}_t}{\partial f_y}& f_x\frac{\partial {\overline{u}}_t}{\partial c_x}+1& f_x\frac{\partial {\overline{u}}_t}{\partial c_y}\\ f_y\frac{\partial {\overline{v}}_t}{\partial f_x}& {\overline{v}}_t+f_y\frac{\partial {\overline{v}}_t}{\partial f_y}& f_y\frac{\partial {\overline{v}}_t}{\partial c_x}& f_y\frac{\partial {\overline{v}}_t}{\partial c_y}+1\end{array}\right]\end{array}$$

$$\begin{array}{r}\because u_t=f_x{\overline{u}}_t+c_x\\ v_t=f_y{\overline{v}}_t+c_y\end{array}$$

 

다음 순서로 $$\begin{array}{r}\left[\begin{array}{cccc}\frac{\partial {\overline{u}}_t}{\partial f_x}& \frac{\partial {\overline{u}}_t}{\partial f_y}& \frac{\partial {\overline{u}}_t}{\partial c_x}& \frac{\partial {\overline{u}}_t}{\partial c_y}\\ \frac{\partial {\overline{v}}_t}{\partial f_x}& \frac{\partial {\overline{v}}_t}{\partial f_y}& \frac{\partial {\overline{v}}_t}{\partial c_x}& \frac{\partial {\overline{v}}_t}{\partial c_y}\end{array}\right]\end{array}$$ 값을 구해야 한다. 우선 $$\begin{array}{r}\left[\begin{array}{ccc}{\overline{u}}_t& {\overline{v}}_t& 1\end{array}\right]\end{array}$$를 전개하면 다음과 같다.

 

$$\begin{array}{rl}{\left[\begin{array}{ccc}{\overline{u}}_t& {\overline{v}}_t& 1\end{array}\right]}^T& ={\rho }_t(\mathbf{R}{\mathbf{X}}_1+\mathbf{t})\\ & ={\rho }_t({\rho }_h^{-1}\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_h+\mathbf{t})\\ & ={\rho }_t{\rho }_h^{-1}(\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_h)+{\rho }_t\mathbf{t}\\ & ={\rho }_t{\rho }_h^{-1}\left[\begin{array}{ccc}& & \\ & \mathbf{R}& \\ & & \end{array}\right]\left[\begin{array}{ccc}{f}_x^{-1}& & -f_x^{-1}{c}_x\\ & f_y^{-1}& -f_y^{-1}{c}_y\\ & & 1\end{array}\right]\left[\begin{array}{c}{u}_h\\ v_h\\ 1\end{array}\right]+{\rho }_t\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\\ & ={\rho }_t{\rho }_h^{-1}\left[\begin{array}{ccc}& & \\ & \mathbf{R}& \\ & & \end{array}\right]\left[\begin{array}{c}{f}_x^{-1}(u_h-c_x)\\ f_y^{-1}(v_h-c_y)\\ 1\end{array}\right]+{\rho }_t\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\\ & ={\rho }_t{\rho }_h^{-1}\left[\begin{array}{c}{r}_{11}{f}_x^{-1}(u_h-c_x)+r_{12}{f}_y^{-1}(v_h-c_y)+r_{13}\\ r_{21}{f}_x^{-1}(u_h-c_x)+r_{22}{f}_y^{-1}(v_h-c_y)+r_{23}\\ r_{31}{f}_x^{-1}(u_h-c_x)+r_{32}{f}_y^{-1}(v_h-c_y)+r_{33}\end{array}\right]+{\rho }_t\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\end{array}$$

 

따라서 ${\overline{u}}_t,{\overline{v}}_t$는 다음과 같이 나타낼 수 있다. 

$$\therefore {\overline{u}}_t=\frac{r_{11}{f}_x^{-1}(u_h-c_x)+r_{12}{f}_y^{-1}(v_h-c_y)+r_{13}+{\rho }_h{t}_x}{r_{31}{f}_x^{-1}(u_h-c_x)+r_{32}{f}_y^{-1}(v_h-c_y)+r_{33}+{\rho }_h{t}_z}$$

$${\overline{v}}_t=\frac{r_{21}{f}_x^{-1}(u_h-c_x)+r_{22}{f}_y^{-1}(v_h-c_y)+r_{23}+{\rho }_h{t}_y}{r_{31}{f}_x^{-1}(u_h-c_x)+r_{32}{f}_y^{-1}(v_h-c_y)+r_{33}+{\rho }_h{t}_z}$$

 

위 식을 사용하여 $$\begin{array}{r}\left[\begin{array}{cccc}\frac{\partial {\overline{u}}_t}{\partial f_x}& \frac{\partial {\overline{u}}_t}{\partial f_y}& \frac{\partial {\overline{u}}_t}{\partial c_x}& \frac{\partial {\overline{u}}_t}{\partial c_y}\\ \frac{\partial {\overline{v}}_t}{\partial f_x}& \frac{\partial {\overline{v}}_t}{\partial f_y}& \frac{\partial {\overline{v}}_t}{\partial c_x}& \frac{\partial {\overline{v}}_t}{\partial c_y}\end{array}\right]\end{array}$$를 구해보면 다음과 같다. 

 

$$\frac{\partial {\overline{u}}_t}{\partial f_x}={\rho }_t{\rho }_h^{-1}(r_{31}{\overline{u}}_t-r_{11})f_x^{-2}(u_h-c_x)$$

$$\frac{\partial {\overline{u}}_t}{\partial f_y}={\rho }_t{\rho }_h^{-1}(r_{32}{\overline{u}}_t-r_{12})f_y^{-2}(v_h-c_y)$$

$$\frac{\partial {\overline{u}}_t}{\partial c_x}={\rho }_t{\rho }_h^{-1}(r_{31}{\overline{u}}_t-r_{11})f_x^{-1}$$

$$\frac{\partial {\overline{u}}_t}{\partial c_y}={\rho }_t{\rho }_h^{-1}(r_{32}{\overline{u}}_t-r_{12})f_y^{-1}$$

$$\frac{\partial {\overline{v}}_t}{\partial f_x}={\rho }_t{\rho }_h^{-1}(r_{31}{\overline{v}}_t-r_{21})f_x^{-2}(u_h-c_x)$$

$$\frac{\partial {\overline{v}}_t}{\partial f_y}={\rho }_t{\rho }_h^{-1}(r_{32}{\overline{v}}_t-r_{22})f_y^{-2}(v_h-c_y)$$

$$\frac{\partial {\overline{v}}_t}{\partial c_x}={\rho }_t{\rho }_h^{-1}(r_{31}{\overline{v}}_t-r_{21})f_x^{-1}$$

$$\frac{\partial {\overline{u}}_t}{\partial c_y}={\rho }_t{\rho }_h^{-1}(r_{32}{\overline{v}}_t-r_{22})f_y^{-1}$$

 

최종적으로 $\frac{\partial {\mathbf{p}}_t}{\partial \mathbf{c}}$는 다음과 같이 나타낼 수 있다.

Camera Intrinsic(4)

$$\begin{array}{rl}\frac{\partial {\mathbf{p}}_t}{\partial \mathbf{c}}& =\left[\begin{array}{cccc}\frac{\partial u_t}{\partial f_x}& \frac{\partial u_t}{\partial f_y}& \frac{\partial u_t}{\partial c_x}& \frac{\partial u_t}{\partial c_y}\\ \frac{\partial v_t}{\partial f_x}& \frac{\partial v_t}{\partial f_y}& \frac{\partial v_t}{\partial c_x}& \frac{\partial v_t}{\partial c_y}\end{array}\right]\\ & =\left[\begin{array}{cccc}{\overline{u}}_t+f_x\frac{\partial {\overline{u}}_t}{\partial f_x}& f_x\frac{\partial {\overline{u}}_t}{\partial f_y}& f_x\frac{\partial {\overline{u}}_t}{\partial c_x}+1& f_x\frac{\partial {\overline{u}}_t}{\partial c_y}\\ f_y\frac{\partial {\overline{v}}_t}{\partial f_x}& {\overline{v}}_t+f_y\frac{\partial {\overline{v}}_t}{\partial f_y}& f_y\frac{\partial {\overline{v}}_t}{\partial c_x}& f_y\frac{\partial {\overline{v}}_t}{\partial c_y}+1\end{array}\right]\\ & =\left[\begin{array}{cccc}{\overline{u}}_t+{\rho }_t{\rho }_h^{-1}{f}_x^{-1}(r_{31}{\overline{u}}_t-r_{11})(u_h-c_x)& {\rho }_t{\rho }_h^{-1}{f}_x{f}_y^{-2}(r_{32}{\overline{u}}_t-r_{12})(v_h-c_y)& {\rho }_t{\rho }_h^{-1}(r_{31}{\overline{u}}_t-r_{11})+1& {\rho }_t{\rho }_h^{-1}{f}_x{f}_y^{-1}(r_{32}{\overline{u}}_t-r_{12})\\ {\rho }_t{\rho }_h^{-1}{f}_x^{-2}{f}_y(r_{31}{\overline{v}}_t-r_{21})(u_h-c_x)& {\overline{v}}_t+{\rho }_t{\rho }_h^{-1}{f}_y^{-1}(r_{32}{\overline{v}}_t-r_{22})(v_h-c_y)& {\rho }_t{\rho }_h^{-1}{f}_x^{-1}{f}_y(r_{31}{\overline{v}}_t-r_{21})& {\rho }_t{\rho }_h^{-1}(r_{32}{\overline{u}}_t-r_{12})+1\end{array}\right]\end{array}$$

 

4.3.3. First Estimate Jacobian (FEJ)

sliding window optimization을 수행하면 매 iteration 마다 state variable $\mathbf{x}$가 업데이트된다. 이 때, $⊞$ 연산자는 N+12개 상태를 각각 파라미터 별로 업데이트해주는 연산자이다. 
$$\mathbf{x}\leftarrow \mathrm{\Delta }\mathbf{x}⊞\mathbf{x}$$

- $\mathbf{x}=[{\rho }_1^{(1)},\cdots ,{\rho }_1^{(N)},\delta {\xi }^T,a,b,\mathbf{c}{]}_{(N+12)\times 1}^T$

 

- ${\mathbf{x}}_0$ : LBA를 시작하는 시점에서 state variable

- $\mathbf{x}$ : LBA가 끝난 후 state variable 

- $\mathrm{\Delta }\mathbf{x}$ : 매 iteration 업데이트(marginalization 포함)로 인한 누적 증분량

- $\delta$ : 매 iteration 업데이트 증분량

 

DSO에서는 LBA를 수행할 때마다 6번의 최적화를 수행하는데 만약 매 iteration마다 Jacobian을 새로 계산하면 다음과 같은 단점이 존재한다. (자세한 내용은 https://blog.csdn.net/heyijia0327/article/details/53707261 참조)

 

1. 연산량이 매우 증가하므로 실시간 성능을 보장할 수 없다.

2. 서로 다른 state의 Jacobian을 한 시스템에서 같이 사용하는 경우 성능의 저하를 일으킬 가능성이 존재한다.

 

따라서 LBA를 수행할 때 매 iteration마다(marginalization 포함) 업데이트로 인해 state variable $\mathbf{x}$가 변하더라도 Jacobian은 새로 계산하지 않고 LBA를 시작하는 시점 (${\mathbf{x}}_0$)에서 계산한 Jacobian을 사용하여 업데이트하는 방법을 First Estimate Jacobian (FEJ)라고 한다. FEJ의 적용 순서는 다음과 같다.

 

1. LBA를 시작하기 전에 현재 $\mathbf{x}$를 ${\mathbf{x}}_0$에 저장한 후 Jacobian을 계산한다. 

$${\mathbf{x}}_0\leftarrow \mathbf{x},\text{ compute }\mathbf{J}{|}_{{\mathbf{x}}_0}$$

2. LBA를 수행하면서 매 iteration마다 업데이트 값을 누적시킨다. 

$$\mathrm{\Delta }\mathbf{x}\leftarrow \mathrm{\Delta }\mathbf{x}+\delta$$

3. 매 iteration동안 Jacobian은 ${\mathbf{x}}_0$에서 계산한값을 사용한다.

4. LBA iteration이 끝난 경우 현재 상태에서 누적된 증분량을 업데이트한다. 

$$\mathbf{x}\leftarrow \mathrm{\Delta }\mathbf{x}⊞{\mathbf{x}}_0$$

 

4.3.4. Adjoint Transformation

앞서 설명한 것과 같이 DSO에서는 하나의 맵포인트에 2개의 키프레임(host, target)이 연결되어 있다. 이에 따라 최적화 수행 시 연산량을 줄이기 위해 target, host 키프레임 사이의 상대 포즈를 기반으로 계산한 Jacobian $\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}$를 사용한다. 하지만 해당 Jacobian을 사용하여 iterative solution을 구하게 되면 두 host, target 키프레임 사이의 상대포즈만 최적화되므로 월드좌표계 $\{W\}$를 기준으로 한 카메라 포즈는 계산할 수 없다. 이 때, DSO에서는 Adjoint Transformation을 통해 $\frac{\partial \mathbf{r}}{\partial {\xi }_{hw}},\frac{\partial \mathbf{r}}{\partial {\xi }_{tw}}$를 계산하여 월드좌표계와 카메라 포즈를 최적화하였다. (자세한 내용은

https://www.cnblogs.com/JingeTU/p/8306727.html 참조)

 

(+23.11.6 SLAMUS님의 수식 오류 지적으로 내용을 수정하였습니다. ${\xi }_h\to {\xi }_{hw},{\xi }_t\to {\xi }_{tw}$)

 

- $\mathbf{r}$ : residual

- ${\xi }_{th}$ : target 기준 host 키프레임의 상대 포즈 변화량 (twist) (6차원 벡터)

- ${\xi }_{hw}$ : 월드좌표계 기준 host 키프레임의 상대 포즈 변화량

- ${\xi }_{tw}$ : 월드좌표계 기준 target 키프레임의 상대 포즈 변화량

 

$\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}$을 $\frac{\partial \mathbf{r}}{\partial {\xi }_{hw}},\frac{\partial \mathbf{r}}{\partial {\xi }_{tw}}$로 변환하기 위해 다음과 같은 연산을 사용한다.

host

$$\begin{array}{rl}{\frac{\partial \mathbf{r}}{\partial {\xi }_{hw}}}^T\frac{\partial \mathbf{r}}{\partial {\xi }_{hw}}& =(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}}{)}^T(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}})\\ & =(\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}}{)}^T(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}{)}^T(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}})(\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}})\end{array}$$

target

$$\begin{array}{rl}{\frac{\partial \mathbf{r}}{\partial {\xi }_{tw}}}^T\frac{\partial \mathbf{r}}{\partial {\xi }_{tw}}& =(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}\frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}}{)}^T(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}\frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}})\\ & =(\frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}}{)}^T(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}}{)}^T(\frac{\partial \mathbf{r}}{\partial {\xi }_{th}})(\frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}})\end{array}$$

 

이 때, twist의 변화량은 다음과 같이 계산할 수 있다. 

$$\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}}=-{\text{Ad}}_{{\mathbf{T}}_{th}}$$

$$\frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}}=\mathbf{I}$$

 

여기서 ${\text{Ad}}_{{\mathbf{T}}_{th}}$를 Adjoint Transformation of SE(3) Group이라고 한다. 해당 변환이 하는 역할은 3차원 공간 상에서 특정 좌표계에서 바라본 twist를 다른 좌표계에서 바라본 twist로 변환하는 역할을 한다.

$${\xi }_{tw}={\text{Ad}}_{{\mathbf{T}}_{th}}\cdot {\xi }_{hw}$$

 

구체적으로 ${\text{Ad}}_{{\mathbf{T}}_{th}}$는 host 키프레임에서 바라본 특정 twist를 target 키프레임에서 바라본 twist로 변환하는 연산자이다. 하지만 해당 공식에서 사용하는 ${\text{Ad}}_{{\mathbf{T}}_{th}}$는 $\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}}$ 값으로 유도되었기 때문에 물리적인 의미는 갖지 않고 $\frac{\partial \mathbf{r}}{\partial {\xi }_{hw}}$를 계산하기 위한 도구로만 사용된다.

${\text{Ad}}_{{\mathbf{T}}_{th}}$의 자세한 정의 및 역할에 대해 알고 싶으면 링크(http://ethaneade.com/lie.pdf)를 참조하면 된다. 

$$\exp ({\text{Ad}}_{{\mathbf{T}}_{th}}\cdot {\xi }_{hw}^{\wedge })={\mathbf{T}}_{th}\exp ({\xi }_{hw}^{\wedge }){\mathbf{T}}_{th}^{-1}$$

 

다음으로 $\frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}}$, $\frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}}$ 값의 유도 과정에 대해 설명한다. 우선 ${\mathbf{T}}_{th}={\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}$와 같이 2개의 포즈로 분할할 수 있고 이를 iterative 업데이트 공식으로 확장하면 다음과 같다.
derivative of host
$$\exp ({\xi }_{th}^{\wedge }+\delta {\xi }_{th}^{\wedge }){\mathbf{T}}_{th}={\mathbf{T}}_{tw}(\exp ({\xi }_{hw}^{\wedge }+\delta {\xi }_{hw}^{\wedge }){\mathbf{T}}_{hw}{)}^{-1}$$

$$\begin{array}{rl}\exp ({\xi }_{th}^{\wedge }+\delta {\xi }_{th}^{\wedge })& ={\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}\exp (-({\xi }_{hw}^{\wedge }+\delta {\xi }_{hw}^{\wedge })){\mathbf{T}}_{th}^{-1}\\ & ={\mathbf{T}}_{th}\exp (-({\xi }_{hw}^{\wedge }+\delta {\xi }_{hw}^{\wedge })){\mathbf{T}}_{th}^{-1}\\ & =\exp (-{\text{Ad}}_{{\mathbf{T}}_{th}}({\xi }_{hw}^{\wedge }+\delta {\xi }_{hw}^{\wedge }))\end{array}$$

$$\therefore \exp ({\xi }_{th}^{\wedge }+\delta {\xi }_{th}^{\wedge })=\exp (-{\text{Ad}}_{{\mathbf{T}}_{th}}({\xi }_{hw}^{\wedge }+\delta {\xi }_{hw}^{\wedge }))$$

$$\therefore \frac{\partial {\xi }_{th}}{\partial {\xi }_{hw}}=-{\text{Ad}}_{{\mathbf{T}}_{th}}$$

 

derivative of target

$$\exp ({\xi }_{th}^{\wedge }+\delta {\xi }_{th}^{\wedge }){\mathbf{T}}_{th}=\exp ({\xi }_{tw}^{\wedge }+\delta {\xi }_{tw}^{\wedge }){\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}$$

$$\begin{array}{rl}\exp ({\xi }_{th}^{\wedge }+\delta {\xi }_{th}^{\wedge })& =\exp ({\xi }_{tw}^{\wedge }+\delta {\xi }_{tw}^{\wedge }){\mathbf{T}}_{tw}{\mathbf{T}}_{hw}^{-1}{\mathbf{T}}_{th}^{-1}\\ & =\exp ({\xi }_{tw}^{\wedge }+\delta {\xi }_{tw}^{\wedge })\end{array}$$

$$\therefore \exp ({\xi }_{th}^{\wedge }+\delta {\xi }_{th}^{\wedge })=\exp ({\xi }_{tw}^{\wedge }+\delta {\xi }_{tw}^{\wedge })$$

$$\therefore \frac{\partial {\xi }_{th}}{\partial {\xi }_{tw}}=\mathbf{I}$$

 

4.3.5. Marginalization

To be added

 

4.3.6. Solving the Incremental Equation

DSO에서는 sliding window 내부에 항상 8개의 키프레임을 유지하면서 12+N개의 파라미터를 최적화한다. (Pose(6) + Photometric(2) + Camera Intrinsics(4) + Idepth(N)). 이렇게 특정 윈도우 내의 키프레임 포즈와 맵포인트를 동시에 최적화하는 방법을 Local Bundle Adjustment (LBA)라고 한다. 이전 섹션에서 유도한 LBA의 에러함수는 다음과 같고 이 때, state variable $\mathbf{x}$는 다음과 같다. 수식을 간결하게 나타내기 위해 idepth를 제외한 나머지 파라미터를 $\mathbf{y}=[\delta {\xi }^{T}ab\mathbf{c}]$로 축약하였다. 

$$f(\mathbf{x})=\sqrt{w_h}\mathbf{r}$$

 

- $$\begin{array}{rl}\mathbf{x}& ={\left[\begin{array}{ccccccc}{\rho }_1^{(1)}& \cdots & {\rho }_1^{(N)}& \delta {\xi }^T& a& b& \mathbf{c}\end{array}\right]}_{(N+12)\times 1}^T\\ & ={\left[\begin{array}{cccc}{\rho }_1^{(1)}& \cdots & {\rho }_1^{(N)}& \mathbf{y}\end{array}\right]}_{(N+12)\times 1}^T\end{array}$$

- ${\rho }_1^{(i)}$ : 1번 이미지에서 i번째 inverse depth 값 (N개)

- $\delta \xi$ : 두 카메라 간 상대 포즈 변화량 (twist) (6차원 벡터) (6개)

- $a,b$ : 두 이미지 간 exposure time을 고려하여 이미지 밝기를 조절하는 파라미터 (2개)

- $\mathbf{c}$ : 카메라 내부 파라미터 (fx,fy,cx,cy) (4개)

 

해당 에러함수를 이용해 least squares optimization 형태로 나타내면 최종적으로 다음과 같은 형태의 식이 유도된다. 해당 식의 유도는 Initialization 챕터에서 다뤘기 때문에 생략한다. 

$$\mathbf{H}\mathrm{\Delta }\mathbf{x}=-\mathbf{b}\to \left[\begin{array}{cc}{\mathbf{H}}_{\rho \rho }& {\mathbf{H}}_{\rho \mathbf{y}}\\ {\mathbf{H}}_{\mathbf{y}\rho }& {\mathbf{H}}_{\mathbf{y}\mathbf{y}}\end{array}\right]\left[\begin{array}{c}\mathrm{\Delta }{\mathbf{x}}_{\rho }\\ \mathrm{\Delta }{\mathbf{x}}_{\mathbf{y}}\end{array}\right]=\left[\begin{array}{c}-{\mathbf{b}}_{\rho }\\ -{\mathbf{b}}_{\mathbf{y}}\end{array}\right]$$

- $\mathbf{y}=[\delta {\xi }^{T}ab\mathbf{c}]$

 

이 때, Hessian Matrix $\mathbf{H}$를 자세하게 펼쳐보면 다음과 같다. 

Schur Complement 섹션에서 설명한 것처럼 ${\mathbf{H}}^{-1}$을 계산하는데 매우 많은 시간이 소모되므로 이를 Schur Complement를 사용해서 $\mathrm{\Delta }{\mathbf{x}}_{\mathbf{y}}$, $\mathrm{\Delta }{\mathbf{x}}_{\rho }$ 순서대로 계산한다.

Details of H and b matrix

$\mathbf{H},\mathbf{b}$ 행렬에 대해 자세하게 전개하면 다음과 같다. 이는 DSO 코드를 보면서 공식과 매칭할 때 어떤 H, b 행렬의 값을 다루고 있는지 확인할 때 참고하면 좋을 것 같다.

$$\left[\begin{array}{cc}{\mathbf{H}}_{\rho \rho }& {\mathbf{H}}_{\rho \mathbf{y}}\\ {\mathbf{H}}_{\mathbf{y}\rho }& {\mathbf{H}}_{\mathbf{y}\mathbf{y}}\end{array}\right]=\left[\begin{array}{cc}{\mathbf{J}}_{\rho }^T{\mathbf{J}}_{\rho }& {\mathbf{J}}_{\rho }^T{\mathbf{J}}_{\mathbf{y}}\\ {\mathbf{J}}_{\mathbf{y}}^T{\mathbf{J}}_{\rho }& {\mathbf{J}}_{\mathbf{y}}^T{\mathbf{J}}_{\mathbf{y}}\end{array}\right]$$

H_yy

$${\mathbf{H}}_{\mathbf{y}\mathbf{y}}={\mathbf{J}}_{\mathbf{y}}^T{\mathbf{J}}_{\mathbf{y}}=\left[\begin{array}{cc}{\mathbf{J}}_{\mathbf{c}}^T{\mathbf{J}}_{\mathbf{c}}& {\mathbf{J}}_{\mathbf{c}}^T{\mathbf{J}}_{{\xi }^{\prime }}\\ {\mathbf{J}}_{{\xi }^{\prime }}^T{\mathbf{J}}_{\mathbf{c}}& {\mathbf{J}}_{{\xi }^{\prime }}^T{\mathbf{J}}_{{\xi }^{\prime }}\end{array}\right]$$

- ${\xi }^{\prime }=[\delta \xi ab{]}_{8\times 1}$

$${\mathbf{J}}_{\mathbf{c}}^T{\mathbf{J}}_{\mathbf{c}}=\left[\begin{array}{ccc}{\frac{\partial {\mathbf{r}}^{(1)}}{\partial \mathbf{c}}}^T& \cdots & {\frac{\partial {\mathbf{r}}^{(N)}}{\partial \mathbf{c}}}^T\end{array}\right]\left[\begin{array}{c}\frac{\partial {\mathbf{r}}^{(1)}}{\partial \mathbf{c}}\\ ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial \mathbf{c}}\end{array}\right]=\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}$$

$${\mathbf{J}}_{\mathbf{c}}^T{\mathbf{J}}_{{\xi }^{\prime }}=\left[\begin{array}{ccc}{\frac{\partial {\mathbf{r}}^{(1)}}{\partial \mathbf{c}}}^T& \cdots & {\frac{\partial {\mathbf{r}}^{(N)}}{\partial \mathbf{c}}}^T\end{array}\right]\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_8}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_8}\end{array}\right]=\left[\begin{array}{ccc}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}\end{array}\right]$$

$${\mathbf{J}}_{{\xi }^{\prime }}^T{\mathbf{J}}_{{\xi }^{\prime }}={\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_8}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_8}\end{array}\right]}^T\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_8}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_8}\end{array}\right]=\left[\begin{array}{ccc}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}\\ ⋮& \ddots & ⋮\\ \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}\end{array}\right]$$

 

H_rho_rho, H_rho_y, H_y_rho

$${\mathbf{J}}_{\rho }^T{\mathbf{J}}_{\rho }={\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(M)}}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(M)}}\end{array}\right]}^T\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(M)}}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(M)}}\end{array}\right]=\left[\begin{array}{cccc}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(1)}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(1)}}& 0& \cdots & 0\\ 0& \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(2)}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(2)}}& \cdots & 0\\ ⋮& ⋮& \ddots & 0\\ 0& 0& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(M)}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(M)}}\end{array}\right]$$

$${\mathbf{J}}_{\mathbf{y}}^T{\mathbf{J}}_{\rho }={\left[\begin{array}{cc}{\mathbf{J}}_{\mathbf{c}}^T& {\mathbf{J}}_{{\xi }^{\prime }}^T\end{array}\right]}^T{\mathbf{J}}_{\rho }={\left[\begin{array}{cc}{\mathbf{J}}_{\mathbf{c}}^T{\mathbf{J}}_{\rho }& {\mathbf{J}}_{{\xi }^{\prime }}^T{\mathbf{J}}_{\rho }\end{array}\right]}^T$$

$${\mathbf{J}}_{\mathbf{c}}^T{\mathbf{J}}_{\rho }=\left[\begin{array}{ccc}{\frac{\partial {\mathbf{r}}^{(1)}}{\partial \mathbf{c}}}^T& \cdots & {\frac{\partial {\mathbf{r}}^{(N)}}{\partial \mathbf{c}}}^T\end{array}\right]\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(M)}}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(M)}}\end{array}\right]=\left[\begin{array}{ccc}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(1)}}& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(M)}}\end{array}\right]$$

$${\mathbf{J}}_{{\xi }^{\prime }}^T{\mathbf{J}}_{\rho }={\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_8}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_1}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_8}\end{array}\right]}^T\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(M)}}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(M)}}\end{array}\right]=\left[\begin{array}{ccc}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(1)}}& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(M)}}\\ ⋮& \ddots & ⋮\\ \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(1)}}& \cdots & \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}}^T\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(M)}}\end{array}\right]$$

 

$f(\mathbf{x})=\sqrt{w_h}\mathbf{r}$ 이므로 huber norm을 생략하고 residual만 표현하면

$$\left[\begin{array}{c}{\mathbf{b}}_{\rho }\\ {\mathbf{b}}_{\mathbf{y}}\end{array}\right]\to \left[\begin{array}{c}{\mathbf{J}}_{\rho }^{T}f(\mathbf{x})\\ {\mathbf{J}}_{\mathbf{y}}^{T}f(\mathbf{x})\end{array}\right]\to \sqrt{w_h}\left[\begin{array}{c}{\mathbf{J}}_{\rho }^T\mathbf{r}\\ {\mathbf{J}}_{\mathbf{y}}^T\mathbf{r}\end{array}\right]$$

 

이 된다. 이를 자세하게 전개하면 다음과 같다.

$${\mathbf{J}}_{\rho }^T\mathbf{r}={\left[\begin{array}{ccc}\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(1)}}{\partial {\rho }^{(M)}}\\ ⋮& \ddots & ⋮\\ \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(1)}}& \cdots & \frac{\partial {\mathbf{r}}^{(N)}}{\partial {\rho }^{(M)}}\end{array}\right]}^T\left[\begin{array}{c}{\mathbf{r}}^{(1)}\\ ⋮\\ {\mathbf{r}}^{(N)}\end{array}\right]=\left[\begin{array}{c}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(1)}}}^T{\mathbf{r}}^{(i)}\\ ⋮\\ \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\rho }^{(M)}}}^T{\mathbf{r}}^{(i)}\end{array}\right]$$

$${\mathbf{J}}_{\mathbf{y}}^T\mathbf{r}=\left[\begin{array}{c}{\mathbf{J}}_{\mathbf{c}}^T\\ {\mathbf{J}}_{{\xi }^{\prime }}^T\end{array}\right]\mathbf{r}=\left[\begin{array}{ccc}{\frac{\partial {\mathbf{r}}^{(1)}}{\partial \mathbf{c}}}^T& \cdots & {\frac{\partial {\mathbf{r}}^{(1)}}{\partial \mathbf{c}}}^T\\ {\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_1}}^T& \cdots & {\frac{\partial {\mathbf{r}}^{(1)}}{\partial {\xi }_8}}^T\\ ⋮& \ddots & ⋮\\ {\frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_1}}^T& \cdots & {\frac{\partial {\mathbf{r}}^{(N)}}{\partial {\xi }_8}}^T\end{array}\right]\left[\begin{array}{c}{\mathbf{r}}^{(1)}\\ ⋮\\ {\mathbf{r}}^{(N)}\end{array}\right]=\left[\begin{array}{c}\sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial \mathbf{c}}}^T{\mathbf{r}}^{(i)}\\ \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_1}}^T{\mathbf{r}}^{(i)}\\ ⋮\\ \sum _{i=1}^N{\frac{\partial {\mathbf{r}}^{(i)}}{\partial {\xi }_8}}^T{\mathbf{r}}^{(i)}\end{array}\right]$$

4.4. Null Space Effect Elimination

4.4.1. Ambiguity Problems

Scale Ambiguity

DSO는 단안카메라를 활용한 Visual Odometry이므로 맵포인트의 깊이를 정확하게 알 수 없는 scale ambiguity 문제를 가진다. 예를 들면, 내가 현재 실제 도시의 이미지를 보고 있는 것인지 도시의 미니어쳐 이미지를 보고 있는 것인지를 단안카메라만 사용하서는 정확하게 알 수 없다는 의미이다. 즉, 카메라의 trajectory와 모든 맵포인트들을 일괄적으로 키우거나 줄여도 최적화 단계에서 아무런 영향을 미치지 않는다. 

또한 모든 카메라 포즈들과 맵포인트에 동일한 SE(3) 변환을 적용하면 이 또한 최적화 단계에서 아무런 영향을 미치지 않는다. 이를 coordinate system ambiguity 문제라고 한다. (자세한 정보는 https://blog.csdn.net/wubaobao1993/article/details/105106301 참조)

 

4.4.2. Null Space

null space란 정방행렬 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$과 벡터 $\mathbf{x}\in {\mathbb{R}}^n$가 존재할 때 다음을 만족하는 해집합을 의미한다. 
$$\mathbf{Ax}=0$$

 

일반적으로 Gauss-Newton (GN) 방법을 사용할 때 다음과 같은 공식을 풀어야 하는 상황이 발생한다.

$$\mathbf{H}\mathrm{\Delta }\mathbf{x}=-\mathbf{b}$$

- $\mathbf{H}={\mathbf{J}}^T\mathbf{J}\in {\mathbb{R}}^{n\times n}$

- $\mathbf{b}={\mathbf{J}}^T\mathbf{e}\in {\mathbb{R}}^n$

- $\mathrm{\Delta }\mathbf{x}\in {\mathbb{R}}^n$

 

만약 $\mathbf{H}$의 역행렬이 존재하는 경우 $\mathrm{\Delta }\mathbf{x}$는 다음과 같은 유일해(unique solution)을 가진다

$$\mathrm{\Delta }\mathbf{x}=-{\mathbf{H}}^{-1}\mathbf{b}\text{if }\mathbf{H}\text{ is invertible}$$

 

$\mathbf{H}$의 역행렬이 존재하지 않는 경우 $\mathrm{\Delta }\mathbf{x}$는 특수해(particular solution) $\mathrm{\Delta }{\mathbf{x}}_p$와 일반해(homogeneous solution) $\mathrm{\Delta }{\mathbf{x}}_h$를 합한 완전해(complete solution)을 갖는다. 
$$\mathrm{\Delta }\mathbf{x}=\mathrm{\Delta }{\mathbf{x}}_h+\mathrm{\Delta }{\mathbf{x}}_p\text{if }\mathbf{H}\text{ is not invertible}$$

우선 비동차방정식(non-homogeneous equation)에서 특수해 $\mathrm{\Delta }{\mathbf{x}}_p$를 구할 수 있다.

$$\mathbf{H}\mathrm{\Delta }{\mathbf{x}}_p=-\mathbf{b}$$

 

다음으로 동차방정식(homogeneous equation)에서 일반해 $\mathrm{\Delta }{\mathbf{x}}_h$를 구할 수 있다.

$$\mathbf{H}\mathrm{\Delta }{\mathbf{x}}_h=0$$

 

따라서 $\mathbf{H}$의 역행렬이 존재하지 않는 경우 완전해는 다음과 같이 나타낼 수 있다. 이 때 $\lambda$는 임의의 정수를 의미하며 $\lambda$ 값에 관계없이 아래 식은 항상 성립하므로 완전해는 무수히 많은 해를 가진다.

$$\mathrm{\Delta }\mathbf{x}=\mathrm{\Delta }{\mathbf{x}}_p+\lambda \mathrm{\Delta }{\mathbf{x}}_h$$

$$\mathbf{H}(\mathrm{\Delta }{\mathbf{x}}_p+\lambda \mathrm{\Delta }{\mathbf{x}}_h)=-\mathbf{b}$$

 

여기서 null space는 $\mathrm{\Delta }{\mathbf{x}}_h$의 해집합으로 인해 span되는 공간을 의미한다. 

$$\mathbf{N}=\text{Span}(\mathrm{\Delta }{\mathbf{x}}_h)$$

 

null space는 전체 방정식의 값에 영향을 미치지 않으므로 null space의 선형결합인 $\mathbf{N}\mathrm{\Delta }\mathbf{x}$ 또한 null space에 포함되어 다음과 같은 방정식이 성립한다.  

$$\mathbf{H}\mathrm{\Delta }\mathbf{x}+\mathbf{N}\mathrm{\Delta }\mathbf{x}=-\mathbf{b}$$

 

4.4.3. Null Space in DSO

null space는 시스템(=에러함수) $\Vert \mathbf{E}(\mathbf{x}+\mathrm{\Delta }\mathbf{x})\Vert$ 값에는 영향을 미치지 않지만 업데이트 값 $\mathrm{\Delta }\mathbf{x}$에는 영향을 미치므로 null space의 영향이 곧 ambiguity 문제의 원인이 된다. 따라서 DSO에서는 LBA를 수행할 때 null space의 영향을 제거하여 ambiguity 문제를 해결하는 방법을 사용했다.

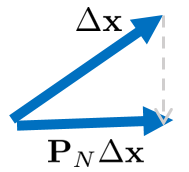
예를 들어 위 그림과 같이 LBA를 통해 업데이트 값 $\mathrm{\Delta }\mathbf{x}=\mathrm{\Delta }{\mathbf{x}}_p+\mathrm{\Delta }{\mathbf{x}}_h$ 이 구해졌다고 가정하면 여기에서 null space에 프로젝션된 양 ${\mathbf{P}}_N\mathrm{\Delta }\mathbf{x}$만큼을 빼줌으로써 null space의 영향을 제거할 수 있다.

프로젝션 행렬 ${\mathbf{P}}_N$은 ${\mathbf{N}}^T\mathbf{N}$의 역행렬이 존재하는가 안하는가에 따라 2가지 방법으로 구할 수 있다.
$$\begin{array}{rl}{\mathbf{P}}_{\mathbf{N}}& ={\mathbf{NN}}^{†}\\ & =\mathbf{N}({\mathbf{N}}^T\mathbf{N}{)}^{-1}{\mathbf{N}}^T\text{if, }{\mathbf{NN}}^T\text{is invertible.}\\ & =\mathbf{N}(\mathbf{V}{\mathrm{\Sigma }}^{†}{\mathbf{U}}^T)\text{if, }{\mathbf{NN}}^T\text{is not invertible. Do SVD}\end{array}$$

 

결론적으로 다음과 같이 최적의 업데이트 값 $\mathrm{\Delta }{\mathbf{x}}^{\ast }$를 계산함으로써 null space의 영향을 제거할 수 있다. 

$$\mathrm{\Delta }{\mathbf{x}}^{\ast }=\mathrm{\Delta }\mathbf{x}-{\mathbf{NN}}^{†}\mathrm{\Delta }\mathbf{x}$$

 

4.4.4. Detailed Derivation of Null Space in DSO

프로젝션 행렬을 사용하지 않고 다른 방법으로 유도하면 다음과 같다. 우선 최적의 업데이트 값 $\mathrm{\Delta }{\mathbf{x}}^{\ast }$는 다음과 같이 나타낼 수 있다. 이 때, $\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h$는 null space에 의해 드리프트된 값을 의미한다.
$$\mathrm{\Delta }{\mathbf{x}}^{\ast }=\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h$$

 

null space가 에러함수의 값에 영향을 미치지 않는다는 점을 사용하면 다음 공식이 성립한다. 

$$\begin{array}{r}\mathbf{E}(\mathbf{x}+\mathrm{\Delta }\mathbf{x})=\mathbf{E}(\mathbf{x}+\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)\end{array}$$

 

위 공식의 두 에러함수를 1차 테일러 전개하여 정리하면 다음과 같이 나타낼 수 있다. 

$$\begin{array}{rl}\mathbf{E}(\mathbf{x}+\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)& =\mathbf{e}(\mathbf{x}+\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T\mathbf{e}(\mathbf{x}+\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)\\ & \simeq (\mathbf{e}(\mathbf{x})+\mathbf{J}(\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h){)}^T(\mathbf{e}(\mathbf{x})+\mathbf{J}(\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h))\\ & =\underset{\mathbf{E}(\mathbf{x}+\mathrm{\Delta }\mathbf{x})}{\underbrace{{\mathbf{e}}^T\mathbf{e}+{\mathbf{e}}^T\mathbf{J}\mathrm{\Delta }\mathbf{x}+\mathrm{\Delta }\mathbf{x}{\mathbf{J}}^T\mathbf{e}+\mathrm{\Delta }{\mathbf{x}}^T{\mathbf{J}}^T\mathbf{J}\mathrm{\Delta }\mathbf{x}}}\underset{\mathrm{\Delta }{\mathbf{x}}_{h}part}{\underbrace{-{\mathbf{e}}^T\mathbf{JN}\mathrm{\Delta }{\mathbf{x}}_h-(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T{\mathbf{J}}^T\mathbf{e}-(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T{\mathbf{J}}^T\mathbf{J}\mathrm{\Delta }\mathbf{x}-\mathrm{\Delta }\mathbf{x}{\mathbf{J}}^T\mathbf{J}(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)+(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T{\mathbf{J}}^T\mathbf{J}(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)}}\\ & =\mathbf{E}(\mathbf{x}+\mathrm{\Delta }\mathbf{x})\end{array}$$

 

따라서 공통부분을 소거한 후 다시 정리하면 다음과 같은 공식이 성립하고 

$$\begin{array}{r}(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T{\mathbf{J}}^T\mathbf{J}(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)={\mathbf{e}}^T\mathbf{JN}\mathrm{\Delta }{\mathbf{x}}_h+(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T{\mathbf{J}}^T\mathbf{e}+(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{)}^T{\mathbf{J}}^T\mathbf{J}\mathrm{\Delta }\mathbf{x}+\mathrm{\Delta }\mathbf{x}{\mathbf{J}}^T\mathbf{J}(\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h)\end{array}$$

 

여기서 null space의 선형결합에 해당하는 $\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h$와 에러함수의 기울기를 의미하는 ${\mathbf{J}}^T\mathbf{e}$는 서로 직교하므로 다음이 성립한다. 
$$\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h{\mathbf{J}}^T\mathbf{e}=0$$

 

따라서 남은 식들을 정리하면 다음 공식이 성립한다.

$$\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h=\mathrm{\Delta }\mathbf{x}$$

 

하지만 위 공식은 실제로 서로 일치하지 않으므로 이를 $\mathrm{\Delta }{\mathbf{x}}_h$에 대한 least squares를 활용하여 근사해를 구하면 $\Vert \mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h-\mathrm{\Delta }\mathbf{x}\Vert$의 크기가 최소가 되는 근사해를 구할 수 있다. 이 때, ${\mathbf{N}}^T\mathbf{N}$의 역행렬이 존재하는가 아닌가에 따라 다음과 같이 해를 구할 수 있다. 
$$\begin{array}{rl}& \mathrm{\Delta }{\mathbf{x}}_h={\mathbf{N}}^{†}\mathrm{\Delta }\mathbf{x}\text{if, }{\mathbf{NN}}^T\text{ is invertible.}\\ & \mathrm{\Delta }{\mathbf{x}}_h=\mathbf{V}{\mathbf{D}}^{†}{\mathbf{U}}^T\mathrm{\Delta }\mathbf{x}\text{if, }{\mathbf{NN}}^T\text{ is not invertible.}\end{array}$$

결론적으로 다음과 같이 최적의 업데이트 값 $\mathrm{\Delta }{\mathbf{x}}^{\ast }$를 계산할 수 있다.

$$\mathrm{\Delta }{\mathbf{x}}^{\ast }=\mathrm{\Delta }\mathbf{x}-\mathbf{N}\mathrm{\Delta }{\mathbf{x}}_h\Rightarrow \mathrm{\Delta }{\mathbf{x}}^{\ast }=\mathrm{\Delta }\mathbf{x}-{\mathbf{NN}}^{†}\mathrm{\Delta }\mathbf{x}$$

 

null space 영향이 제거된 ${\mathbf{H}}^{\ast },{\mathbf{b}}^{\ast }$를 다음과 같이 유도할 수 있다.

$$\begin{array}{rl}\mathrm{\Delta }{\mathbf{x}}^T{\mathbf{b}}^{\ast }& =\mathrm{\Delta }{\mathbf{x}}^T\mathbf{b}-\mathrm{\Delta }{\mathbf{x}}_h^T{\mathbf{b}}_n\\ & =\mathrm{\Delta }{\mathbf{x}}^T\mathbf{b}-({\mathbf{N}}^{†}\mathrm{\Delta }\mathbf{x}{)}^T{\mathbf{N}}^T{\mathbf{J}}^T\mathbf{e}\\ & =\mathrm{\Delta }{\mathbf{x}}^T\mathbf{b}-\mathrm{\Delta }{\mathbf{x}}^T({\mathbf{NN}}^{†}{)}^T\mathbf{b}\\ & =\text{where, }{\mathbf{b}}_n={\mathbf{J}}_n\mathbf{e}{\mathbf{J}}_n=\frac{\partial \mathbf{e}}{\partial \mathrm{\Delta }{\mathbf{x}}_h}=\frac{\partial \mathbf{e}}{\partial \mathrm{\Delta }\mathbf{x}}\frac{\partial \mathrm{\Delta }\mathbf{x}}{\partial \mathrm{\Delta }{\mathbf{x}}_h}=\mathbf{JN}\end{array}$$

$$\begin{array}{rl}\mathrm{\Delta }{\mathbf{x}}^T{\mathbf{H}}^{\ast }\mathrm{\Delta }\mathbf{x}& =\mathrm{\Delta }{\mathbf{x}}^T\mathbf{H}\mathrm{\Delta }\mathbf{x}-\mathrm{\Delta }{\mathbf{x}}_h^T{\mathbf{H}}_n\mathrm{\Delta }{\mathbf{x}}_h\\ & =\mathrm{\Delta }{\mathbf{x}}^T\mathbf{H}\mathrm{\Delta }\mathbf{x}-({\mathbf{N}}^{†}\mathrm{\Delta }\mathbf{x}{)}^T{\mathbf{N}}^T{\mathbf{J}}^T\mathbf{JN}({\mathbf{N}}^{†}\mathrm{\Delta }\mathbf{x})\\ & =\mathrm{\Delta }{\mathbf{x}}^T\mathbf{H}\mathrm{\Delta }\mathbf{x}-\mathrm{\Delta }{\mathbf{x}}^T({\mathbf{NN}}^{†}{)}^T\mathbf{H}({\mathbf{NN}}^{†})\mathrm{\Delta }\mathbf{x}\\ & \text{where, }{\mathbf{H}}_n={\mathbf{J}}_n^T{\mathbf{J}}_n,{\mathbf{J}}_n=\frac{\partial \mathbf{e}}{\partial \mathrm{\Delta }{\mathbf{x}}_h}=\frac{\partial \mathbf{e}}{\partial \mathrm{\Delta }\mathbf{x}}\frac{\partial \mathrm{\Delta }\mathbf{x}}{\partial \mathrm{\Delta }{\mathbf{x}}_h}=\mathbf{JN}.\end{array}$$

 

따라서 최종적으로 다음의 연산을 통해 null space의 영향을 제거할 수 있다.

$${\mathbf{b}}^{\ast }=\mathbf{b}-({\mathbf{NN}}^{†}{)}^T\mathbf{b}$$

$${\mathbf{H}}^{\ast }=\mathbf{H}-({\mathbf{NN}}^{†}{)}^T\mathbf{H}({\mathbf{NN}}^{†})$$

 

 

5. Pixel Selection

5.1. Make Histogram

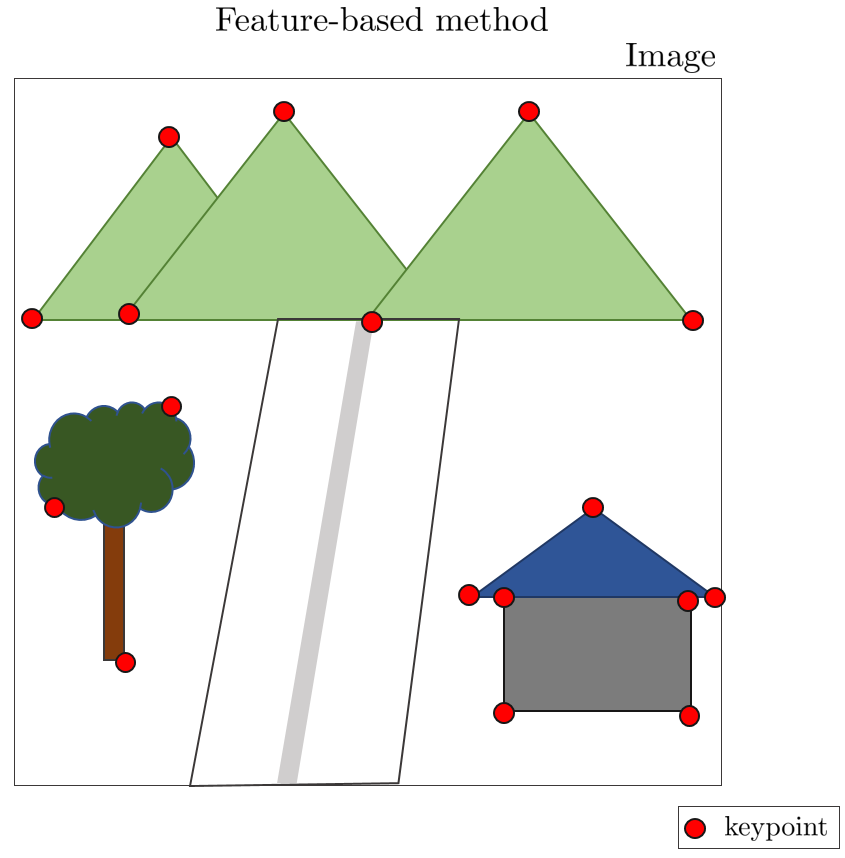
ORB-SLAM2와 같은 feature-based VO의 경우 이미지 내에서 특정 포인트를 추출할 때 feature extraction 알고리즘을 사용하여 키포인트를 추출한다. 그 다음 해당 키포인트를 3차원 점으로 Unprojection ${\pi }^{-1}(\cdot )$하고 다시 2차원 점으로 Reprojection $\pi (\cdot )$해서 reprojection error를 사용하여 카메라의 모션을 계산한다. 

하지만 direct method를 사용하는 DSO는 키포인트를 추출하는 과정없이 특정 픽셀의 밝기 오차를 계산하기 때문에 특정 포인트를 추출하는 방법 또한 feature-based와 달라지게 된다. DSO에서는 이미지에서 특정 포인트를 추출하기 위해 gradient histogram과 dynamic grid 방법을 사용했다. 해당 방법은 DSO 논문에서도 자세한 설명이 부족하고 참고 논문이 없으며 구글링해도 나오는 정보가 거의 없으므로 해당 섹션에서 다루는 내용이 100% 정확하다고 볼 수 없다. 해당 내용은 논문을 볼 때 참고용으로 보면 좋을 것 같다. 

 

1. 우선 새로운 이미지가 들어오면 gradient histogram을 생성하기 위해 이미지를 32x32 영역으로 나눈다. (grayscale) 

2. 하나의 영역을 확대해서 보면 아래 그림과 깉이 여러 픽셀들로 구성되어 있고 각 픽셀마다 고유의 밝기 값을 가지고 있다. 이를 이용해 image gradient (dx,dy)를 구할 수 있고 해당 영역에 대한 히스토그램을 만들 수 있다. 

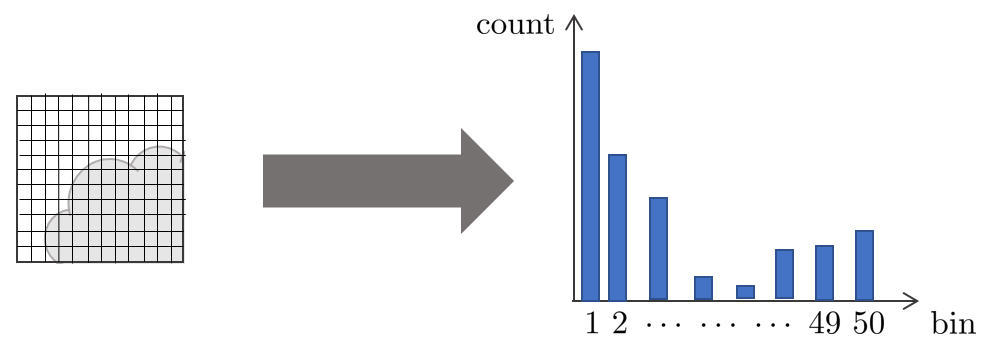
3. 이 때, gradient $dx,dy$는 원래 0~255 값을 가지지만 DSO에서는 한 픽셀의 bin = $\sqrt{d{x}^2+d{y}^2}$ 값을 사용하여 히스토그램을 생성했다.
$$0<\sqrt{d{x}^2+d{y}^2}<360$$

bin은 위와 같은 범위를 가지지만 이를 1~50 범위로 제한하여 50이 넘는 경우 최대값을 50으로 설정하여 히스토그램의 범위를 단순화했다.

 

4. 이러한 히스토그램을 32x32 모든 영역에 대해 계산한다.

5. 히스토그램에서 total count의 50%가 되는 bin 값을 1-50 순서대로 찾는다. 예를 들어, 히스토그램의 모든 bin에서 총 1000개가 카운트되었다면 1번 bin부터 순서대로 카운트 값을 빼주면서 해당 값이 500보다 작아지는 bin을 threshold로 설정한다. 또한, 주변 3x3 영역의 threshold 평균을 사용한 smoothed threshold 값 또한 설정한다.

5.2. Dynamic Grid

한 이미지에 대한 32x32 히스토그램을 생성하고 threshold 값을 설정하였으면 다음으로 dynamic grid 방법을 통해 이미지 내에서 픽셀을 선택한다. 이를 통해 high gradient 영역에 대부분의 포인트가 추출되는 것을 방지하고 한 이미지 내에서 추출할 수 있는 총 포인트의 개수(N=2000)을 관리할 수 있다. 

 

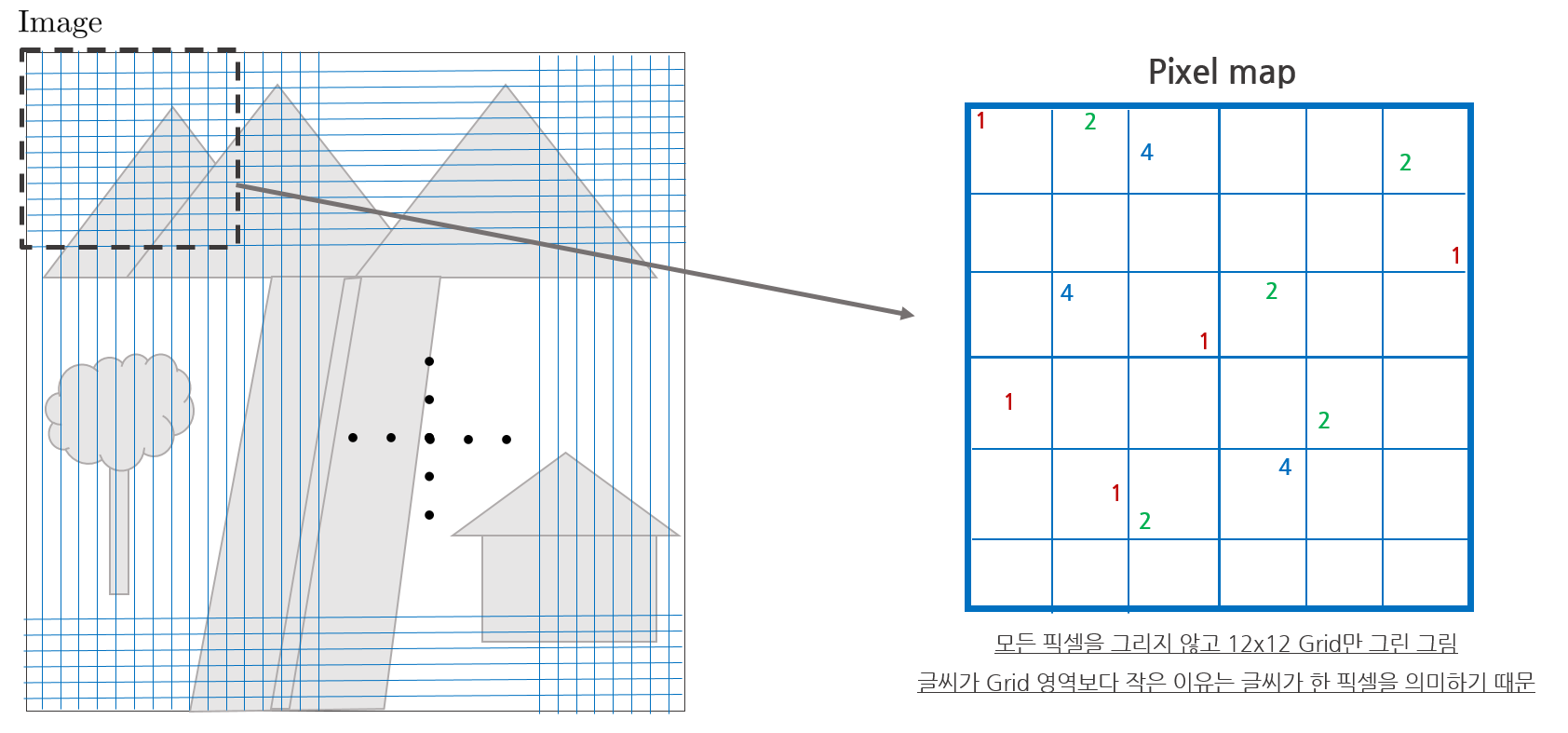
1. 하나의 grid 영역의 크기를 설정한다. DSO는 초기값으로 12x12 [pixel]을 사용했다. 640x480 이미지 기준으로 봤을 때 일반적으로 32x32 histogram 영역보다 작은 크기를 사용한다. grid 크기를 설정하였으면 이미지 전체를 grid로 나눈다. 

 

2. 한 grid 영역을 확대해보면 아래와 같다. 이 때, 한 영역에서 총 3개의 피라미드 이미지의 gradient를 사용한다. Alalagong님의 자료를 참조하여 피라미드 별로 파란색(lv2), 초록색(lv1), 빨간색(lv0, 원본)으로 표시하면 아래 그림과 같고 순서대로 해당 영역의 픽셀을 탐색한다.

3. 피라미드 레벨이 낮은 곳(lv0, 원본)부터 한 픽셀 씩 루프를 돌면서 해당 영역 히스토그램의 smoothed threshold 값과 픽셀의 squared gradient $\sqrt{d{x}^2+d{y}^2}$ 값을 비교한다. (111 -> 112 -> 113 -> ... -> 119 -> 11 -> 1 -> 121 -> 122 -> 123 -> ... -> 129 -> 12 -> 2 -> ...) 

이 때, 특정 픽셀 값이 smoothed treshold보다 크면 다음 단계로써 해당 픽셀의 $(dx,dy)$ 값과 랜덤한 방향벡터인 randdir과 norm을 계산하여 해당 값이 0보다 큰 지 검사한다. 

$$\text{randdir}\cdot (dx,dy)>0$$

 

4. 최종적으로 norm까지 특정 값보다 크다면 해당 픽셀을 grid를 대표하는 픽셀로 선정하고 루프를 탈출한다. 

ex) 만약 115 픽셀의 $\sqrt{d{x}^2+d{y}^2}$ 값이 smoothed threshold보다 크고 $\text{randdir}\cdot (d{x}_{115},d{y}_{115})>0$를 만족하면 115 픽셀을 grid 대표 픽셀로 선정하고 루프를 탈출한다. 랜덤한 방향벡터와 norm을 계산함으로써 특정 픽셀 영역에 포인트 추출이 몰리는 현상을 방지했다.

5. 만약 픽셀이 smoothed threshold보다 작은 경우 lv0 -> lv1 -> lv2 순서로 값을 비교한다. 이 때, 레벨이 높을수록 threshold에 0.75를 곱한 후 픽셀의 밝기 값과 비교하여 높은 피라미드 레벨의 픽셀일수록 추출될 확률을 높였다.

 

6. 모든 픽셀을 전부 검사했음에도 추출한 포인트의 총합이 원하는 총량(기본 N=2000)보다 적을 경우 ($N_{\text{want}}/N_{\text{have}}>1.25$)에는 8x8로 한 grid 크기를 줄인 후 다시 검색하고 만약 추출된 포인트가 너무 많은 경우 ($N_{\text{want}}/N_{\text{have}}<0.25$)에는 16x16 grid 크기로 포인트를 다시 추출한다.

7. 한 이미지 내에서 모든 grid에 대해 루프를 돌면서 smoothed threshold를 통과한 픽셀들만 pixel map에 저장한다. pixel map에는 lv0에서 추출된 포인트의 경우 '1', lv1에서 추출된 포인트는 '2', lv3에서 추출된 포인트는 '4'의 값을 갖는다. 포인트가 추출되지 않는 영역의 값은 '0'을 갖는다. 

 

6. Code Review

 

 

 

References

1. [EN] DSO paper

2. [KR] SLAMKR study 

3. [CH] DSO code reading

4. [CH] jingeTU's SLAM blog

5. [CH] DSO tracking and optimization

6. [CH] DSO initialization

7. [CH] Detailed in DSO

8. [CH] DSO photometric calibration

9. [CH] DSO code with comments

10.[CH] DSO Null Space

11. [CH] DSO (5) Calculation and Derivation of Null Space

12. [KR] goodgodgd's Visual Odometry and vSLAM

13.[EN] DSO Photometric Calibration paper