본 포스트는 공부 목적으로 작성하였습니다.
혹시 보시는 도중 잘못된 부분이나 개선할 부분이 있다면 댓글이나 메일주시면 확인 후 수정하도록 하겠습니다.
해당 포스트는 앞서 pdf 파일로 정리했던 자료를 포스팅한 글입니다.
자세한 내용은 다음 링크를 통해 확인해주세요.
https://www.facebook.com/groups/slamkr/permalink/858942477798731/
본 논문은 LOAM의 저자가 작성한 visual odometry 관련 논문이고 IROS 2014에 게재되었다. 해당 논문에서 설명하는 DEMO는 추후 LOAM과 결합하여 V-LOAM이 된다.
최근 Image + Depth가 있는 상태에서 visual odometry를 계산하는 방법들이 많이 연구되고 있다. 하지만 depth가 이미지를 전부 커버하지 못하므로 이미지 영역 내에는 unknown depth 영역이 존재할 수 밖에 없다. 따라서 해당 논문에서는 위 문제를 극복하기 위해 sparse depth 상태에서도 camera motion을 지속적으로 추정하는 방법을 제안한다. 또한 bundle adjustment(iSAM)를 사용하여 motion estimation 값들을 최적화하는 방법 또한 제안한다.
Hardware System Overview
논문에서 사용한 디바이스의 스펙은 다음과 같다.

- 30 [hz] RGB and depth image
- 640x480 resolution
- 58 deg HFV

- 60 [hz] RGB image from camera
- 744x470 resolution
- 83 deg HFV
- Hokuyo UTM-30LX 3D LiDAR
- 180 deg FOV with 180 deg resolution
- 40 lines/s
Notation and Task Description

- $k, k \in Z^{+}$ : k번째 이미지 프레임
- $\{C\}$ : 카메라 3D 좌표계
: 원점은 카메라의 optical center에 있다
: x축은 center 기준으로 좌측이며 y축은 윗방향이다. z축은 카메라의 주축(principal axis)방향과 일치한다.
- $\mathcal{I}$ : $\{C^{k}\}$에서 추출한 visual feature들의 집합
- $\mathbf{X}^{k}_{i}$, $i \in \mathcal{I}$ : $\{C^{k}\}$에서 추출한 i번째 visual feature의 좌표(depth를 알고 있는 경우).
- $\bar{\mathbf{X}}^{k}_{i}$ : $\{C^{k}\}$에서 추출한 i번째 visual feature의 좌표 (depth를 모르고 있는 경우). depth 값을 모르므로 z값을 1로 정규화했다.
$$\mathbf{X}^{k}_{i} = [ x^{k}_{i}, \ y^{k}_{i}, \ z^{k}_{i} ]^{T}$$
$$\bar{\mathbf{X}}^{k}_{i} = [ \bar{x}^{k}_{i}, \ \bar{y}^{k}_{i}, \ 1 ]^{T}$$
Software System Overview
전체적인 시스템의 구성은 아래 그림과 같다.


Kanade Lucas Tomasi(KLT) 트래커를 사용하여 harris corner를 추적하는 모듈. 해당 모듈에서 추적된 visual feature들은 Depth Map Registration 모듈에서 depth 값과 결합된다(associated).

depth 데이터를 estimated motion에 따라 맵에 등록(registration)시키는 모듈. 해당 모듈에서 visual feature와 depth 값이 결합된다. depth map에 없는 visual feature의 경우 triangulation을 통해 depth 값을 추정하게 된다.

visual feature(+depth)를 입력으로 받아서 motion estimation을 수행하는 모듈. known depth, unknown depth의 경우를 모두 처리하여 motion estimation을 수행한다.

iSAM 라이브러리를 사용하여 estimated motion의 누적된 오차를 제거해주는 모듈. user-defined camera model을 사용할 수 있기 때문에 iSAM 라이브러리를 사용했다. 0.25 ~ 1 [hz]의 주기로 동작한다.

Frame to Frame Motion의 high-frequency transform과 BA의 low-frequency transform을 입력으로 받아 최종 transform을 반환하는 모듈. 최종적으로 Frame to Frame Motion의 주기로 transform을 반환한다.
Frame to Frame Motion Estimation
visual feature $\mathbf{X}_{i}$의 카메라 모션은 다음과 같이 나타낼 수 있다.
$$\mathbf{X}_{i}^{k}= \mathbf{R}\mathbf{X}_{i}^{k-1}+ \mathbf{T}$$
- $\mathbf{R} \in \mathbb{R}^{3\times3}$
- $\mathbf{T} \in \mathbb{R}^{3}$
Known Depth
위 식에서 두 frame(k,k-1) 중 하나의 depth 정보만 사용하면 문제를 단순화시킬 수 있다. 본 논문에서는 현재 시점에서 바로 직전 frame인 $\{C^{k-1}\}$의 depth 정보만 사용한다. 이전 frame $\{C^{k-1}\}$에서 depth를 아는 feature의 경우 $\mathbf{X}_{i}^{k-1}$과 같이 나타낼 수 있다. 현재 frame $\{C^{k}\}$에는 아직 depth map이 등록되지 않은 상태이므로 $\mathbf{X}_{i}^{k}$를 정확하게 알 수 있다. 따라서 normalized term을 사용하여 $\bar{\mathbf{X}}_{i}^{k}$로 표기한다.
$\mathbf{X}_{i}$의 카메라 모션은 다음과 같이 작성할 수 있다.
$$z_{i}^{k}\bar{\mathbf{X}}_{i}^{k}=\mathbf{R}\mathbf{X}_{i}^{k-1}+\mathbf{T}$$
벡터 형태로 풀어서 쓰면 다음과 같이 나타낼 수 있다.
$$z^{k}_{i}\begin{bmatrix}
\bar{x}^{k}_{i}\\
\bar{y}^{k}_{i}\\
1
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{R}_{1}\\
\mathbf{R}_{2}\\
\mathbf{R}_{3}
\end{bmatrix}
\begin{bmatrix}
x^{k-1}_{i}\\
y^{k-1}_{i}\\
z^{k-1}_{i}
\end{bmatrix}
+
\begin{bmatrix}
T_{1}\\
T_{2}\\
T_{3}
\end{bmatrix}$$
위 벡터 식을 1st, 2nd, 3rd row로 각각 전개한 다음 $z^{k}_{i}$를 소거하면 다음과 같은 식을 얻을 수 있다.

$$(\mathbf{R}_{1}-\bar{x} _{i}^{k}\mathbf{R}_{3})\mathbf{X}_{i}^{k-1}+T_{1}-\bar{x} _{i}^{k}T_{3}=0$$
$$(\mathbf{R}_{2}-\bar{y} _{i}^{k}\mathbf{R}_{3})\mathbf{X}_{i}^{k-1}+T_{2}-\bar{y} _{i}^{k}T_{3}=0$$
Unknown Depth
unknown depth의 경우 known depth와는 다르게 $\mathbf{X}_{i}^{k-1}$를 정확히 모르는 경우를 의미한다. ($\mathbf{X}_{i}^{k-1} \rightarrow \bar{\mathbf{X}}_{i}^{k-1}$) 따라서 $\{C^{k-1}\}$, $\{C^{k}\}$의 visual feature 모두 depth를 모르는 상태이므로 다음과 같이 표기할 수 있다.
$$z_{i}^{k}\bar{\mathbf{X}}_{i}^{k}=z^{k-1}_{i}\mathbf{R}\bar{\mathbf{X}}_{i}^{k-1}+\mathbf{T}$$
위 벡터 식을 1st, 2nd, 3rd row로 각각 전개한 다음 $z^{k}_{i}$와 $z^{k-1}_{i}$를 소거하면 다음과 같은 식을 얻을 수 있다.
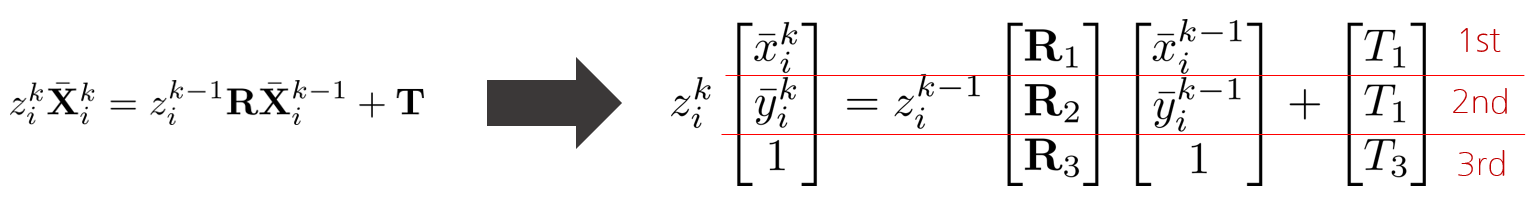
$$[-\bar{y} _{i}^{k}T_{3}+T_{2},\bar{x} _{i}^{k}T_{3}-T_{1}, -\bar{x} _{i}^{k}T_{2}+\bar{y} _{i}^{k}T_{1}]\mathbf{R}\bar{\mathbf{X}}_{i}^{k-1}=0$$
따라서 지금까지 총 3개의 공식을 유도하였다.
$$(\mathbf{R}_{1}-\bar{x} _{i}^{k}\mathbf{R}_{3})\mathbf{X}_{i}^{k-1}+T_{1}-\bar{x} _{i}^{k}T_{3}=0$$
$$(\mathbf{R}_{2}-\bar{y} _{i}^{k}\mathbf{R}_{3})\mathbf{X}_{i}^{k-1}+T_{2}-\bar{y} _{i}^{k}T_{3}=0$$
$$[-\bar{y} _{i}^{k}T_{3}+T_{2},\bar{x} _{i}^{k}T_{3}-T_{1}, -\bar{x} _{i}^{k}T_{2}+\bar{y} _{i}^{k}T_{1}]\mathbf{R}\bar{\mathbf{X}}_{i}^{k-1}=0$$
이 때, 회전행렬 $\mathbf{R}$은 rodrigues fomular에 의해 $\theta$의 반대칭행렬(skew symmeric matrix)인 $\hat{\theta}$로 나타낼 수 있다.
Rodrigues formula
$$\mathbf{R} = e^{\hat{\theta}} = \mathbf{I} + \frac{\hat{\theta}}{\left \| \theta \right \|}\sin\left \| \theta \right \| + \frac{\hat{\theta}^{2}}{\left \| \theta \right \|^{2}}(1-\cos\left \| \theta \right \|)$$
- $\theta = [\theta_{x}, \ \theta_{y}, \ \theta_{z}]^{T}$
- $\hat{\theta} = \begin{bmatrix}
0 & -\theta_{z} & \theta_{y} \\
\theta_{z} & 0 & -\theta_{x} \\
-\theta_{y} & \theta_{x} & 0
\end{bmatrix}$
rodrigues formula를 통해 위 known, unknwon 공식에 $\mathbf{R}$을 치환하여 정리하면 $[\mathbf{T}; \theta]$ 파라미터로 표현할 수 있는 공식들이 얻어진다. 이렇나 공식들을 m개의 known depth와 n개의 unknwon depth 길이를 가진 함수로 표현하면 다음과 같은 비선형 함수를 얻을 수 있다.
$$\mathbf{f}([\mathbf{T};\theta]) = \varepsilon$$
- $\mathbf{f} \in \mathbb{R}^{2m+n}$
- $\varepsilon \in \mathbb{R}^{2m+n \times 1}$
위 식에서 jacobian matrix $\mathbf{J} = \frac{\partial f}{\partial[\mathbf{T};\theta]}$를 구하여 Levenberg-Marquardt (LM) 방법을 통해 비선형 최적화를 수행한다. 이 때, $\lambda$는 LM 방법의 scale factor이다.
$$[T;\theta]^{T}\leftarrow[T;\theta]^{T}-(\mathbf{J}^{T}\mathbf{J}+\lambda \text{diag}(\mathbf{J}^{T}\mathbf{J}))^{-1}\mathbf{J}^{T}\epsilon$$
해당 모듈의 전체적인 과정은 다음과 같다.

Feature Depth Association
해당 섹션에서는 visual feature와 depth를 결합하는 방법에 대해 설명한다. depth map은 센서를 통해 얻은 포인트클라우드의 집합을 의미한다. 현재 카메라 영역에 존재하는 포인트들만 사용하고 카메라 영역 외부에 있는 경우 특정 시간이 지나면 자동으로 제거된다. depth map은 균일한 feature density를 위해 다운사이징되어 일정한 angular interval을 갖는다.
depth map 위에 존재하는 점은 spherical coordinate로 변환할 수 있다.
$$p = [r, \theta, \varphi]$$
- [radial distance, azimuthal angle, polar angle]
그리고 depth map과 visual feature 사이의 일치하는 점을 찾기 위해 우선 2개의 angular coordinate $[\theta, \varphi]$를 2d KD-tree 형태로 정렬한다. 그리고 해당 visual feature와 가장 가까운 3개의 점을 depth map에서 찾는다. 이 때, 4개의 점을 사용하여 아래의 공식을 통해 해당 visual feature의 depth 값을 계산할 수 있다.

위 방법으로 depth를 구할 수 없는 경우에는 해당 visual feature가 존재하는 가장 처음과 마지막 프레임 간 triangulation을 통해 depth를 추정한다.
Bundle Adjustment
Frame to Frame Motion Estimation 모듈을 통해 나온 값들은 Bundle Adjustment 모듈에서 주기적으로 조정된다. 이 때, processin time과 accuracy를 동시에 만족시키기 위해 5장의 이미지마다 한 장 씩($\{C^{5k}\}$)BA의 입력으로 들어간다. 총 8장의 이미지가 입력으로 들어오면 BA를 수행한다. 실제 코드 상에서 BA를 수행하기 위해 unser-define camera model을 지원하는 iSAM 라이브러리를 사용하였다.

BA의 순차적인 과정은 다음과 같다.
1. 모든 visual feature들을 $\{C^{l}\}$로 프로젝션시킨다. 이렇게 프로젝션 된 feature의 좌표는 $\tilde{\mathbf{X}}^{l}_{i}$로 표기한다.
$$\tilde{\mathbf{X}}^{k}_{i} = [\bar{x}^{k}_{i},\ \bar{y}^{k}_{i},\ z^{k}_{i}]^{T}$$
- $i\in \mathcal{I}$
2. $\tilde{\mathbf{X}}^{l}_{i}$을 $\{C^{l}\}$에서 $\{C^{j}\}$로 변환시켜주는 transform 행렬을 $\mathcal{T}_{l}^{j}$로 정의한다.
- $j\in \mathcal{J}\backslash \{l\}$ (l을 제외한 $\mathcal{J} $ 집합의 원소라는 의미)
3. 이 때, BA는 두 개의 연속적인 프레임 사이의 motion transform과 $\tilde{\mathbf{X}}^{l}_{i}$ 값을 조정하면서 다음 함수를 최소화시킨다.
$$\min\sum_{i, j}(\mathcal{T}_{l}^{j}(\tilde{\mathbf{X}}_{i}^{l})-\tilde{\mathbf{X}}_{i}^{j})^{T}\Omega_{i}^{j} (\mathcal{T}_{l}^{j}(\tilde{\mathbf{X}}_{i}^{l})-\tilde{\mathbf{X}}_{i}^{j})$$
- $i\in \mathcal{I}, j\in \mathcal{J}\backslash \{l\}$
여기서 $\tilde{\mathbf{X}}_{i}^{j}$는 $\{C^{j}\}$에서 i번째 feature의 관측값을 의미한다. 그리고 $\Omega_{i}^{j}$는 information matrix를 의미한다.
$$\Omega^{j}_{i} = \begin{bmatrix}
\Omega_{11} & \Omega_{12} & \Omega_{13} \\
\Omega_{21} & \Omega_{22} & \Omega_{23} \\
\Omega_{31} & \Omega_{32} & \Omega_{33}
\end{bmatrix}$$
여기서 대각 성분인 $\Omega_{11},\Omega_{22}$는 상수값이고 $\Omega_{33}$는 depth에 따라 값이 다르다.
$$\begin{cases}
\Omega_{33} = \text{larger value} & \text{ if } \text{Known Depth} \\
\Omega_{33} = \text{smaller value} & \text{ if } \text{ Triangulation} \\
\Omega_{33} = 0 & \text{ if } \text{Unknown Depth}
\end{cases}$$
해당 BA 모듈은 0.25 ~ 1 [hz] 주기로 동작하며 최종 결과값을 Transform Integration 모듈로 전달한다.
'Engineering' 카테고리의 다른 글
| [SLAM] g2o example 코드 리뷰 (0) | 2022.06.09 |
|---|---|
| [SLAM] Visual LiDAR Odometry and Mapping (V-LOAM) 논문 리뷰 (0) | 2022.06.08 |
| [SLAM] Direct Sparse Odometry (DSO) 논문 및 코드 리뷰 (2) (11) | 2022.06.03 |
| [SLAM] Direct Sparse Odometry (DSO) 논문 및 코드 리뷰 (1) (5) | 2022.06.03 |
| [SLAM] Lidar Odometry And Mapping (LOAM) 논문 리뷰 (29) | 2022.06.02 |
 A L I D A
A L I D A





