[SLAM] Optical Flow와 Direct Method 개념 및 코드 리뷰

본 포스트에서는 optical flow와 direct method의 개념을 리뷰한다. direct method 관련 내용은 [4]에서 대부분의 내용을 참고했다.

Optical flow

Optical flow는 시간 경과에 따른 이미지 간 픽셀 이동을 계산하는 알고리즘을 말한다. Opticalflow는 이미지의 밝기 변화를 기반으로 알고리즘을 계산하기 때문에 다음과 같은 key assumption들이 존재한다

  1. 밝기 항상성 (brightness consistency) : 어떤 물체의 픽셀은 프레임이 바뀌어도 그 값이 변하지 않아야 한다. gray 영상의 경우 추적하고 있는 물체의 픽셀 밝기는 변하지 않는다고 가정한다.

  2. 작은 움직임 (small motion) : 영상 내에서 움직임은 그다지 빠르지 않다고 가정한다. 즉, 영상 내에서 물체의 움직임보다 시간의 변화가 더 빠르게 진행된다.

  3. 공간 일관성 (spatial coherence) : 공간적으로 서로 인접하는 점들은 동일한 객체에 속할 가능성이 높고 동일한 움직임을 갖는다고 가정한다.

Formular derivation

위와 같이 영상 내의 한 점 (x,y)가 있을 때 미소시간(dt)동안 이동한 점의 밝기(intensity)는 변하지 않는다.

\begin{equation}
\begin{aligned}  
\mathbf{I}(x,y,t) = \mathbf{I}(x+dx,y+dy,t+dt)
\end{aligned} 
\end{equation}

 

 

위 식에 1차 테일러 전개를 적용함으로써 아래와 같은 식을 유도할 수 있다.

\begin{equation}
\begin{aligned}  
\mathbf{I}(x+dx,y+dy,t+dt) \approx \mathbf{I}(x,y,t) + \frac{\partial \mathbf{I}}{\partial x}dx + \frac{\partial \mathbf{I}}{\partial y}dy + \frac{\partial \mathbf{I}}{\partial t}dt
\end{aligned} 
\end{equation}

\begin{equation}
\begin{aligned}  
\therefore \frac{\partial \mathbf{I}}{\partial x}dx + \frac{\partial \mathbf{I}}{\partial y}dy + \frac{\partial \mathbf{I}}{\partial t}dt = 0
\end{aligned} 
\end{equation}

 

위 두번째 공식에서 양변을 dt로 나누고 정리해준다.

\begin{equation}
\begin{aligned}  
\frac{\partial \mathbf{I}}{\partial x}\frac{dx}{dt} + \frac{\partial \mathbf{I}}{\partial y}\frac{dy}{dt} = -\frac{\partial \mathbf{I}}{\partial t}
\end{aligned} 
\end{equation}

 

위 공식에서 픽셀이 어느방향 $(\frac{dx}{dt},\frac{dy}{dt})$으로 움직여야 해당 공식이 0이 되는가? 또는 0에 가까워지는가?를 찾는 것이 optical flow 문제의 핵심이다. 즉, 최적의 $(\frac{dx}{dt},\frac{dy}{dt})$ 값을 구하는 것이 optical flow 문제가 된다. 이를 간단하게 표현하면 다음과 같다.

\begin{equation}
\begin{aligned}  
\mathbf{I}_{x} \dot{x} + \mathbf{I}_{y} \dot{y} = -\mathbf{I}_{t}
\end{aligned} 
\end{equation}

- $\frac{dx}{dt} = \dot{x}$ : 시간에 따른 x의 변화량 (찾고자 하는 값)

- $\frac{dy}{dt} = \dot{y}$ : 시간에 따른 x의 변화량 (찾고자 하는 값)

- $\frac{\partial \mathbf{I}}{\partial x} = \mathbf{I}_{x}$ : x 방향 이미지 그라디언트(gradient)

- $\frac{\partial \mathbf{I}}{\partial y} = \mathbf{I}_{y}$ : y 방향 이미지 그라디언트(gradient)

- $\frac{\partial \mathbf{I}}{\partial t} = \mathbf{I}_{t}$ : 이전 이미지와 현재 이미지에서 동일 픽셀의 밝기 변화

 

다시 행렬로 표현하면 다음과 같다.

\begin{equation} \label{eq:opt1}
\boxed{ \begin{aligned}  
\begin{bmatrix}
      \mathbf{I}_{x} && \mathbf{I}_{y} 
      \end{bmatrix}
      \begin{bmatrix}
      \dot{x}  \\ \dot{y}
      \end{bmatrix} = -\mathbf{I}_{t}
\end{aligned}  }
\end{equation}

 

LK optical flow

(\ref{eq:opt1})은 식은 1개인데 반해 미지수는 2개($\dot{x}, \dot{y}$)이므로 해를 구할 수 없다. 따라서 해를 구하기 위해 작은 로컬 윈도우 내에서 픽셀들은 동일한 모션을 갖는다고 가정하는데 이러한 방법을 Lucas-Kanade (LK) Optical Flow라고 한다.  윈도우의 크기는 $w^{2}$의 픽셀 수를 포함하는 $w \times w$ 크기로 설정한다. 

\begin{equation}
\begin{aligned}  
\begin{bmatrix}
\mathbf{I}_{x,1} & \mathbf{I}_{y,1} \\
\mathbf{I}_{x,2} & \mathbf{I}_{y,2} \\
\vdots & \vdots \\
\mathbf{I}_{x,k} & \mathbf{I}_{y,k} \\
\end{bmatrix}
\begin{bmatrix}
\dot{x}  \\ \dot{y}
\end{bmatrix} & = 
\begin{bmatrix} -\mathbf{I}_{t,1} \\ -\mathbf{I}_{t,2} \\ \vdots \\ -\mathbf{I}_{t,k}  \end{bmatrix} \quad \text{ where, } \ k = 1,\cdots,w^{2} 
\end{aligned} 
\end{equation}

위 식은 $\mathbf{A} \begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix} = -\mathbf{b}$의 선형 방정식 형태를 갖는다. 그리고 미지수보다 방정식이 많은 over-determined system이므로 해가 존재하지 않는다. 한 프레임의 각 픽셀 윈도우를 설정하고 다음 프레임에서 이 윈도우와 가장 잘 일치하는 곳을 찾는다. 작은 지역 윈도우를 사용하기 때문에 이 윈도우보다 큰 움직임이 발생했을 경우 움직임을 계산하지 못하는 단점이 있다. 이러한 문제를 해결하기 위해 이미지 피라미드를 사용할 수 있다.

 

최종적으로 least square의 정규방정식을 통하여 최적의 근사해 $\dot{x}, \dot{y}$를 구한다.

\begin{equation}
\boxed{ \begin{aligned}  
\begin{bmatrix} \dot{x} \\ \dot{y} \end{bmatrix}^{*} &= -(\mathbf{A}^{\intercal}\mathbf{A})^{-1}\mathbf{A}^{ \intercal }\mathbf{b} \\
& = -\begin{bmatrix} \sum_i \mathbf{I}_{x,i}^2 & \sum_i \mathbf{I}_{x,i} \mathbf{I}_{y,i} \\ \sum_i \mathbf{I}_{x,i} \mathbf{I}_{y,i} & \sum_i \mathbf{I}_{y,i}^2 \end{bmatrix}^{-1} \begin{bmatrix} \sum_i \mathbf{I}_{x,i} \mathbf{I}_{t,i} \\ \sum_i \mathbf{I}_{y,i} \mathbf{I}_{t,i} \end{bmatrix} \\
& = -\frac{1}{\mathbf{D}}\begin{bmatrix} \sum_i \mathbf{I}_{y,i}^2 & -\sum_i \mathbf{I}_{x,i} \mathbf{I}_{y,i} \\ -\sum_i \mathbf{I}_{x,i} \mathbf{I}_{y,i} & \sum_i \mathbf{I}_{x,i}^2 \end{bmatrix} \begin{bmatrix} \sum_i \mathbf{I}_{x,i} \mathbf{I}_{t,i} \\ \sum_i \mathbf{I}_{y,i} \mathbf{I}_{t,i} \end{bmatrix}
\end{aligned}  }
\end{equation}

- $(\mathbf{A}^{\intercal}\mathbf{A})^{-1} \in \mathbb{R}^{2\times 2}$ : $2\times 2$ 정방 행렬의 역행렬 공식이 적용된다.
- $\mathbf{D} = \sum_i \mathbf{I}_{x,i}^2\sum_i \mathbf{I}_{y,i}^2 - \Big( \sum_i \mathbf{I}_{x,i}\mathbf{I}_{y,i} \Big)^2$

 

위 식을 통해 근사해 $\dot{x}, \dot{y}$를 구했으면 기존 $x,y$ 좌표에 더해줌으로써 다음 이미지에서 포인트의 위치를 예측한다.

\begin{equation}
\begin{aligned}  
& x \leftarrow x + dx \\
& y \leftarrow y + dy \\
\end{aligned}  
\end{equation}

- $dx = \dot{x}\cdot dt$

- $dy = \dot{y}\cdot dt$

 

Direct method

Direct method는 밝기 변화를 통해 photometric error를 최소화하는 카메라의 포즈를 계산한다. Direct method도 opticalflow와 동일하게 이미지의 밝기 변화를 기반으로 알고리즘을 계산하기 때문에 다음과 같은 key assumption들이 존재한다

 

  1. 밝기 항상성 (brightness consistency) : 어떤 물체의 픽셀은 프레임이 바뀌어도 그 값이 변하지 않아야 한다. gray 영상의 경우 추적하고 있는 물체의 픽셀 밝기는 변하지 않는다고 가정한다.

  2. 작은 움직임 (small motion) : 영상 내에서 움직임은 그다지 빠르지 않다고 가정한다. 즉, 영상 내에서 물체의 움직임보다 시간의 변화가 더 빠르게 진행된다.

  3. 공간 일관성 (spatial coherence) : 공간적으로 서로 인접하는 점들은 동일한 객체에 속할 가능성이 높고 동일한 움직임을 갖는다고 가정한다.

 

Visual odmetry (VO)의 종류 중 하나인 feature-based와 비교했을 때 direct method의 장단점은 다음과 같다.

Pros

  1. 이미지의 모든 정보를 사용 가능

  2. keypoint, descriptor 계산 시간 생략

  3. feature matching이 힘든 경우에도 사용 가능 (low texture 환경)

  4. semi-dense 또는 dense 매핑 가능 

Cons

  1. gradient에 전적으로 의존하는 목적 함수

  2. gray scale 값이 불변한다는 강력한 가정

 

Photometric error

NOMENCLATURE of photometric error

• $\tilde{\mathbf{p}}_{2} = \pi_{h}(\cdot) : \begin{bmatrix} X' \\ Y' \\ Z' \\1 \end{bmatrix} \rightarrow   \begin{bmatrix} X'/Z' \\ Y'/Z' \\ 1  \end{bmatrix}   = \begin{bmatrix} \tilde{u}_{2} \\ \tilde{v}_{2} \\ 1 \end{bmatrix}$    
  • 이미지 평면에 프로젝션하기 위해 3차원 공간 상의 점 $\mathbf{X}'$를 non-homogeneous 변환한 점
• $\mathbf{p}_{2} = \pi_{k}(\cdot) = \tilde{\mathbf{K}} \tilde{\mathbf{p}}_{2} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \end{bmatrix} \begin{bmatrix} \tilde{u}_{2} \\ \tilde{v}_{2} \\ 1 \end{bmatrix}= \begin{bmatrix} f\tilde{u} + c_{x} \\ f\tilde{v} + c_{y} \end{bmatrix} = \begin{bmatrix} u_{2} \\ v_{2} \end{bmatrix}$
  
  • 렌즈 왜곡을 보정한 후 이미지 평면에 프로젝션한 점. 만약 왜곡 보정이 입력 단계에서 이미 수행된 경우 $\pi_{k}(\cdot) = \tilde{\mathbf{K}}(\cdot)$이 된다.
• $\mathbf{K} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \\ 0 & 0 & 1 \end{bmatrix}$: 카메라 내부(intrinsic) 파라미터 
• $\tilde{\mathbf{K}} = \begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y}  \end{bmatrix}$: $\mathbb{P}^{2} \rightarrow \mathbb{R}^{2}$로 프로젝션하기 위해 내부 파라미터의 마지막 행을 생략했다.
• $\mathcal{P}$:  이미지 내의 모든 특징점들의 집합
• $\mathbf{e}(\mathbf{T}) \rightarrow \mathbf{e}$: 일반적으로 표기를 생략하여 간단하게 나타내기도 한다. 
• $\mathbf{p}^{i}_{1}, \mathbf{p}^{i}_{2}$: 첫번째 이미지와 두번째 이미지에서 i번째 특징점의 픽셀 좌표
• $\oplus$ : 두 SE(3) 군을 결합(composition)하는 연산자
• $\mathbf{J} = \frac{\partial \mathbf{e}}{\partial \mathbf{T}} = \frac{\partial \mathbf{e}}{\partial [\mathbf{R}, \mathbf{t}]}$
• $\mathbf{X}' = [X,Y,Z,1]^{\intercal} = [\tilde{\mathbf{X'}}, 1]^{\intercal} = \mathbf{TX}$
• $\mathbf{T}\mathbf{X}$: Transformation, 3차원 점 $\mathbf{X}$를 카메라 좌표계로 변환, $\bigg( \mathbf{T}\mathbf{X} = \begin{bmatrix} \mathbf{R} \mathbf{X} + \mathbf{t} \\ 1 \end{bmatrix}  \in \mathbb{R}^{4\times1} \bigg)$
• $\mathbf{X}' = [X',Y',Z',1]^{\intercal} = [\tilde{\mathbf{X}}', 1]^{\intercal}$
• $\xi = [\mathbf{w}, \mathbf{v}]^{\intercal} = [w_{x}, w_{y}, w_{z}, v_{x}, v_{y}, v_{z}]^{\intercal}$: 3차원 각속도와 속도로 구성된 벡터. twist라고 불린다.
• $[\xi]_{\times} = \begin{bmatrix} [\mathbf{w}]_{\times} & \mathbf{v} \\ \mathbf{0}^{\intercal} & 0 \end{bmatrix} \in \text{se}(3)$ : hat 연산자가 적용된 twist의 lie algebra (4x4 행렬)

 

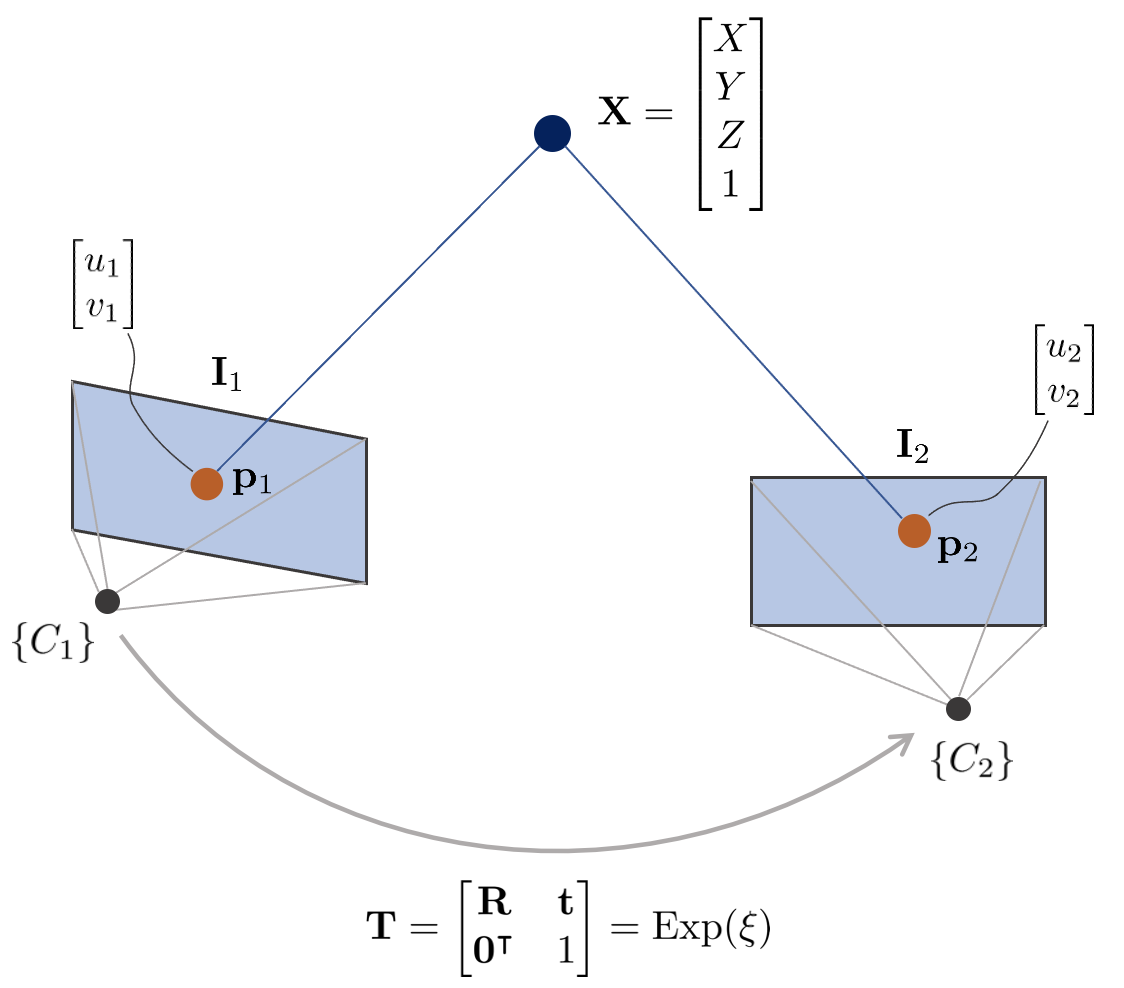
위 그림에서 3차원 점 $\mathbf{X}$의 월드 좌표는 $[X,Y,Z,1]^{\intercal} \in \mathbb{P}^{3}$이고 이에 대응하는 두 카메라 이미지 평면 상의 픽셀 좌표는 $\mathbf{p}_{1}, \mathbf{p}_{2} \in \mathbb{P}^{2}$이다. 이 때, 두 카메라 $\{C_{1}\}, \{C_{2}\}$의 내부 파라미터 $\mathbf{K}$는 동일하다고 가정한다. 카메라 $\{C_{1}\}$을 원점($\mathbf{R} = \mathbf{I}, \mathbf{t} = \mathbf{0}$)이라고 했을 때 픽셀 좌표 $\mathbf{p}_{1}, \mathbf{p}_{2}$를 3차원 점 $\mathbf{X}$을 통해 표현하면 아래와 같은 순서로 프로젝션된다.

\begin{equation}
\begin{aligned}
\mathbf{p}_{1}  = \begin{pmatrix}
u_{1}\\v_{1}\end{pmatrix}
& = \pi(\mathbf{X}) = \pi_{k}(\pi_{h}(\mathbf{X}))   \\
\mathbf{p}_{2}  = \begin{pmatrix} u_{2}\\ v_{2}\end{pmatrix} & = \pi(\mathbf{TX}) = \pi_{k}(\pi_{h}(\mathbf{TX}))    \\ \end{aligned}
\end{equation} 

 

 

 

direct method의 특징 중 하나는 feature-based와 달리 어떤 $\mathbf{p}_{2}$가 $\mathbf{p}_{1}$과 매칭하는지 알 수 있는 방법이 없다. 따라서 현재 포즈 추정치를 기반으로 $\mathbf{p}_{2}$의 위치를 찾는다. 즉, 카메라의 포즈를 최적화하여 $\mathbf{p}_{2}$와 $\mathbf{p}_{1}$을 유사하게 만드는데 이 때 photometric 에러를 최소화하여 문제를 해결한다. photometric 에러는 다음과 같다.

\begin{equation}
\boxed{
\begin{aligned}
\mathbf{e}(\mathbf{T}) & =  \mathbf{I}_{1}(\mathbf{p}_{1})-\mathbf{I}_{2}(\mathbf{p}_{2}) \\
& = \mathbf{I}_{1} \bigg( \pi_{k}(\pi_{h}(\mathbf{X})) \bigg)-\mathbf{I}_{2}\bigg(  \pi_{k}(\pi_{h}(\mathbf{TX})) \bigg) \\
\end{aligned} }
\end{equation}

 

photometric 에러는 grayscale 불변성 가정에 기반하며 스칼라 값을 가진다. photometric 에러를 통해 non-linear least squares를 풀기 위해 다음과 같은 cost function $\mathbf{E}(\mathbf{T})$를 정의할 수 있다.

\begin{equation}
  \begin{aligned}
 \mathbf{E}(\mathbf{T}) & =  \arg\min_{\mathbf{T}^{*}} \sum_{i \in \mathcal{P}} \left\| \mathbf{e}_{i} \right\|^{2} \\
& = \arg\min_{\mathbf{T}^{*}} \sum_{i \in \mathcal{P}} \mathbf{e}_{i}^{\intercal}\mathbf{e}_{i} \\
& = \arg\min_{\mathbf{T}^{*}} \sum_{i \in \mathcal{P}} \Big( \mathbf{I}_{1}(\mathbf{p}^{i}_{1})-\mathbf{I}_{2}(\mathbf{p}^{i}_{2}) \Big)^{\intercal} \Big( \mathbf{I}_{1}(\mathbf{p}^{i}_{1})-\mathbf{I}_{2}(\mathbf{p}^{i}_{2}) \Big)
  \end{aligned}
\end{equation}

 

 

$\mathbf{E}(\mathbf{T}^{*})$를 만족하는 $\left\|\mathbf{e}(\mathbf{T}^{*})\right\|^{2}$를 non-linear least squares를 통해 반복적으로 계산할 수 있다. 작은 증분량 $\Delta \mathbf{T}$를 반복적으로 $\mathbf{T}$에 업데이트함으로써 최적의 상태를 찾는다. 
\begin{equation}
  \begin{aligned}
    \mathbf{E}(\mathbf{T} + \Delta \mathbf{T}) & = \arg\min_{\mathbf{T}^{*}} \sum_{i \in \mathcal{P}} \left\|\mathbf{e}_{i}(\mathbf{T} + \Delta \mathbf{T})\right\|^{2} 
  \end{aligned}
\end{equation}

 

엄밀하게 말하면 상태 증분량 $\Delta \mathbf{T}$은 SE(3) 변환행렬이므로 $\oplus$ 연산자를 통해 기존 상태 $\mathbf{T}$에 더해지는게 맞지만 표현의 편의를 위해 $+$ 연산자를 사용하였다. 

\begin{equation}
  \begin{aligned}
\mathbf{T}  \oplus \Delta \mathbf{T}  \quad  \rightarrow \quad \mathbf{T} + \Delta \mathbf{T}
  \end{aligned}
\end{equation}

 

이는 1차 테일러 근사를 통해 다음과 같이 표현이 가능하다.
\begin{equation}
  \begin{aligned}
    \mathbf{e}(\mathbf{T} + \Delta \mathbf{T}) & \approx \mathbf{e}_{i}(\mathbf{T}) + \mathbf{J}\Delta \mathbf{T}  \\
& = \mathbf{e}_{i}(\mathbf{T}) + \frac{\partial \mathbf{e}}{\partial \mathbf{T}}\Delta \mathbf{T}
  \end{aligned}
\end{equation}

 

 

이를 미분하여 최적의 증분량 $\Delta \mathbf{T}^{*}$ 값을 구하면 다음과 같다. 자세한 유도 과정은 본 문서에서는 생략한다. 유도 과정에 대해 자세히 알고 싶으면 SLAM] Errors and Jacobian Derivations for SLAM 정리 포스트를 참조하면 된다.
\begin{equation}
  \begin{aligned}
    & \mathbf{J}^{\intercal}\mathbf{J} \Delta \mathbf{T}^{*} = -\mathbf{J}^{\intercal}\mathbf{e} \\ 
    & \mathbf{H}\Delta \mathbf{T}^{*} = - \mathbf{b} \\
  \end{aligned} \label{eq:1}
\end{equation}

Jacobian of the photometric error

(\ref{eq:1})를 수행하기 위해서는 photometric 에러에 대한 자코비안 $\mathbf{J}$을 구해야 한다. 이는 다음과 같이 나타낼 수 있다.

\begin{equation}
  \begin{aligned}
    \mathbf{J} & = \frac{\partial \mathbf{e}}{\partial \mathbf{T}}   \\
& =  \frac{\partial \mathbf{e}}{\partial [\mathbf{R}, \mathbf{t}]} 
  \end{aligned}
\end{equation}

 

이를 자세히 풀어서 보면 다음과 같다.

\begin{equation}
  \begin{aligned}
\mathbf{J} = \frac{\partial \mathbf{e}}{\partial \mathbf{T}} & = \frac{\partial }{\partial \mathbf{T}} \bigg(
\mathbf{I}_{1} \bigg(    \pi_{k}(\pi_{h}(\mathbf{X}))   \bigg)-\mathbf{I}_{2}\bigg( \pi_{k}(\pi_{h}(\mathbf{TX})) \bigg) \bigg) \\
& =  \frac{\partial }{\partial \mathbf{T}} \bigg( -\mathbf{I}_{2}\bigg( \pi_{k}(\pi_{h}(\mathbf{TX})) \bigg) \bigg) \\ & =  \frac{\partial }{\partial \mathbf{T}} \bigg( -\mathbf{I}_{2}\bigg( \pi_{k}(\pi_{h}(\mathbf{X}')) \bigg) \bigg)
  \end{aligned}
\end{equation}

 

 

자코비안 $\mathbf{J}$은 다음과 같다. 

\begin{equation}
\boxed{
  \begin{aligned}
\mathbf{J} = \frac{\partial \mathbf{e}}{\partial \Delta \xi} & =  \frac{\partial \mathbf{I}}{\partial \mathbf{p}_{2}} \frac{\partial \mathbf{p}_{2}}{\partial \tilde{\mathbf{p}}_{2}} \frac{\partial \tilde{\mathbf{p}}_{2}}{\partial \mathbf{X}'} \frac{\partial \mathbf{X}'}{\partial \Delta \xi}  \\
& = \begin{bmatrix} \nabla \mathbf{I}_{u} & \nabla \mathbf{I}_{v} \end{bmatrix} 
\begin{bmatrix} f & 0 & c_{x} \\ 0 & f & c_{y} \end{bmatrix}
\begin{bmatrix} \frac{1}{Z'} & 0 & \frac{-X'}{Z'^{2}} & 0 \\ 0 & \frac{1}{Z'} & \frac{-Y'}{Z'^{2}}&0\\ 0 & 0 & 0 & 0\end{bmatrix}
\begin{bmatrix} -[\tilde{\mathbf{X}}']_{\times} & \mathbf{I} \\ \mathbf{0}^{\intercal} & \mathbf{0}^{\intercal}  \end{bmatrix} \\
 & = \begin{bmatrix} \nabla \mathbf{I}_{u} & \nabla \mathbf{I}_{v} \end{bmatrix}  \begin{bmatrix} \frac{f}{Z'} & 0 & -\frac{fX}{Z'^{2}} & 0\\ 0 & \frac{f}{Z'} & -\frac{fY}{Z'^{2}} & 0\end{bmatrix}
    \begin{bmatrix} 0 & Z' & -Y' & 1 & 0 & 0 \\ -Z' & 0 & X' & 0 & 1 & 0 \\ Y'& -X'& 0 & 0 & 0 & 1 \\ 0 & 0 & 0&0&0&0\end{bmatrix} \\
    & = \begin{bmatrix} \nabla \mathbf{I}_{u} & \nabla \mathbf{I}_{v} \end{bmatrix}  \begin{bmatrix} -\frac{fX'Y'}{Z'^{2}} & \frac{f(1 + X'^{2})}{Z'^{2}} & -\frac{fY'}{Z'} & \frac{f}{Z'} & 0 & -\frac{fX'}{Z'^{2}} \\
      -\frac{f(1+Y'^{2})}{Z'^{2}} & \frac{fX'Y'}{Z'^{2}} & \frac{fX'}{Z'} & 0 & \frac{f}{Z'} & -\frac{fY'}{Z'^{2}} \end{bmatrix} \in \mathbb{R}^{1 \times 6}
  \end{aligned} }
\end{equation}

자세한 자코비안의 유도 과정은 [SLAM] Errors and Jacobian Derivations for SLAM 정리 포스트를 참조하면 된다.

 

Coarse-to-fine scheme

본 섹션에서는 direct method에서 일반적으로 성능 개선을 위해 사용하는 coarse-to-fine 방법에 대해 설명한다. Coarse-to-fine 방법이란 이미지 피라미드를 사용하여 높은 피라미드에서 대략(coarse)적인 카메라 움직임 계산한 후 점차적으로 낮은 피라미드로 낮춰가면서 정밀(fine)한 카메라 움직임 계산까지 진행하는 알고리즘을 의미한다.

 

이전 섹션에서 설명한 photometric error 모델의 경우 단일 픽셀 $\mathbf{u}$ 의 intensity 변화만을 파라미터로 사용하기 때문에 픽셀의 이동 범위가 큰 빠른 움직임(rapid motion)이 있는 영상 내에서는 정상적으로 동작하지 않는다. 실제 영상 내의 급격한 픽셀의 움직임을 추적하기 위해서는 영상 처리 알고리즘이 이미지 크기의 10-15%를 커버할 수 있어야 한다. 따라서 이를 개선하기 위해 이미지 피라미드와 이미지 패치 방식의 photometric error 모델을 사용하여 높은 피라미드 레벨에서 카메라의 대략(coarse)적인 움직임을 계산한 후 낮은 피라미드 레벨까지 순차적으로 내려오면서 정밀(fine)하게 움직임을 계산해야 한다.

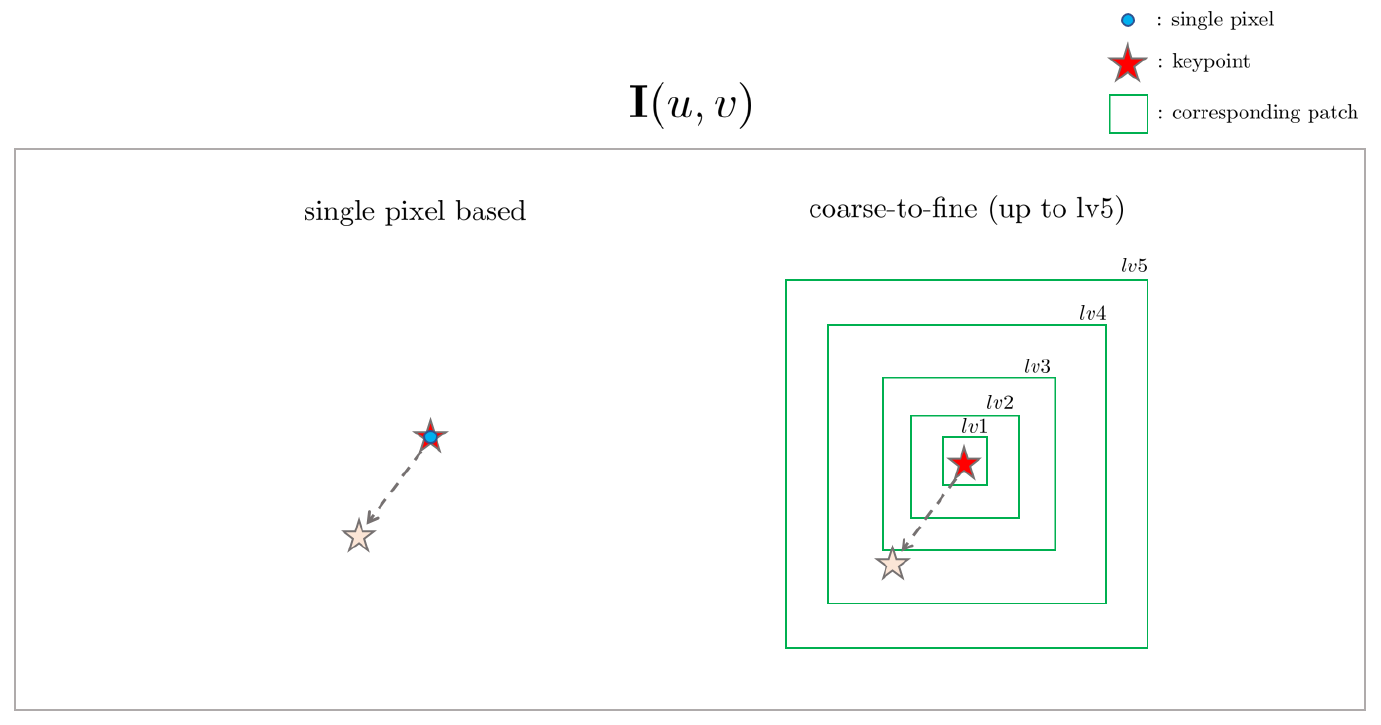
위 그림은 기존의 단일 픽셀 기반 photometric error 계산 모델과 coarse-to-fine 모델의 차이를 나타낸 그림이다. 위 그림 왼쪽과 같이 단일 픽셀 방법의 경우 키포인트의 이동 범위가 커지면, 즉 image velocity가 커지면 매우 높은 확률로 추적에 실패하여 전체적인 pose tracking 성능이 낮아진다. 반면, 위 그림 오른쪽과 같이 coarse-to-fine 방법의 경우 각 레벨 별 이미지 패치를 통해 높은 레벨부터 대략적으로(coarse) 픽셀의 이동을 추적하여 작은 레벨로 갈수록 점차적으로 정밀(fine)하게 픽셀의 이동을 추적할 수 있다.

 

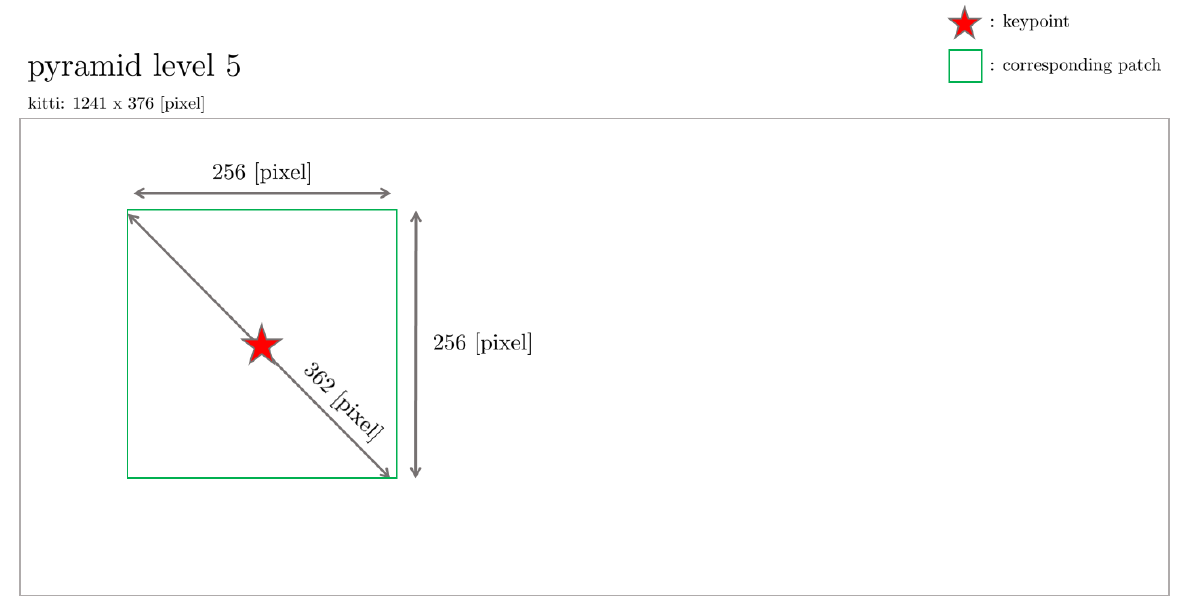
이와 같은 multi-level pyramid 방법의 경우 이미지 내에서 픽셀의 위치 변화에 대한 가속도(image velocity)를 처리할 수 있는 범위를 계산할 수 있다. 현재 적용된 가장 높은 단계인 level 5에서 처리할 수 있는 image velocity를 생각해보자. 우선 level 5의 image patch 크기를 KITTI 원본 이미지 1241 x 376 [pixel]에 복원시킬 경우 위 그림과 같이 8 x 8 [pixel] $\rightarrow$ 256 x 256 [pixel] 이 된다. 따라서 이론적으로 pyramid level 5가 처리할 수 있는 최대 image velocity는 아래와 같다.

\begin{equation}
  \begin{aligned}
    \begin{bmatrix}
      \dot{u} \\ \dot{v}
    \end{bmatrix}_{level5} =
    \begin{bmatrix}
      256 \\ 256
    \end{bmatrix}
  \end{aligned}
\end{equation}

 

하지만 이는 이론적인 값으로써 실제 픽셀이 위와 같이 ($\dot{u}, \dot{v}$) = (256,256) 속도로 움직일 때 추적이 가능하다는 보장이 없다. 따라서 실제 패치 크기의 절반인 128 x 128 [pixel] 정도의 image velocity를 처리할 수 있다고 판단하는 것이 더 합리적이다. 결론적으로 level 5의 경우 ($\dot{u}, \dot{v}$) = (128, 128)의 속도로 움직이는 물체를 추적이 가능하다고 예상된다. 이는 kitti 데이터에서는 ($u\,v$) = (10.3%, 34.0%)를 의미한다.

 

Outlier rejection

본 섹션에서는 Non-linear Least Square Optimization에서 일반적으로 성능 개선을 위해 사용하는 threshold-based outlier rejection 방법과 huber loss function에 대해 설명한다. Coarse-to-fine 방법이 적용된 direct method 방법의 경우에도 종종 이미지 패치 추적에 실패하는 경우가 발생한다. 추적에 실패한 이미지 패치의 경우 photometric eror가 급격하게 증가하면서 전체적인 pose tracking 성능을 저하시킨다. 이렇게 추적에 실패하여 큰 에러를 가지는 이미지 패치를 outlier로 처리하여 성능을 보존하는 방법을 outlier rejection 방법이라고 부르며 크게 다음과 같은 두 가지 방법으로 분류할 수 있다.

Threshold-based

residual의 값이 특정 threshold 이상으로 커지는 경우 optimization에서 제외하는 방법을 말한다.

Parameterized robust kernels

Robust estimator를 사용하여 큰 에러로 인한 시스템 성능의 영향을 감소시키는 방법을 말한다. DSO는 기본적으로 huber robust estimator를 사용한다. Huber robust estimator(or loss/kernel function)은 매우 큰 에러를 갖는 outlier의 loss를 down-weighting 시킴으로써 loss의 영향력을 줄여주는 robust loss function 중 하나이다.

\begin{equation}
\begin{aligned}
\rho(\mathbf{e}) =
\begin{cases}
\frac{1}{2}\mathbf{e}^{2} & \text{ for } \left | \mathbf{e} \right | \le \delta \\
\delta(\left | \mathbf{e} \right | - \frac{1}{2}\delta) & \text{ otherwise }
\end{cases}
\end{aligned}
\end{equation}

huber (green), original (blue)

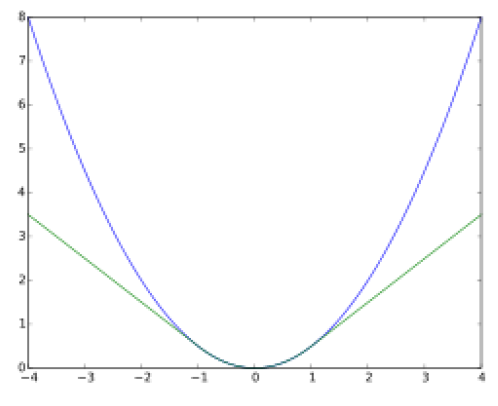
위 그림은 huber loss가 적용된 에러 함수와 원래 에러 함수를 비교한 그림이다. 그림과 같이 huber loss는 에러가 일정 $\delta$ 값 이하일 때는 2차 함수 형태로써 weighting이 반영되지만 $\delta$ 값 이상으로 커지는 경우 1차 직선 함수로 weighting된다. 이 때, $\mathbf{e}$ 는 에러를 의미하며 huber threshold $\delta$ 값을 변경하면서 에러가 시스템에 미치는 영향을 변경할 수 있다.

 

Code review

본 섹션에서는 [4] 책의 Chapter 8에서 소개한 direct method 코드를 리뷰한다. 코드는 링크를 통해 확인할 수 있다.

project3Dto2D

inline Eigen::Vector2d project3Dto2D(float x, float y, float z, float fx, float fy, float cx, float cy)
{
  float u = fx*x/z+cx;
  float v = fy*y/z+cy;
  return Eigen::Vector2d ( u,v );
}

위 함수는 3차원 점을 2차원 픽셀 좌표로 projection하는 함수이다.

$$u = c_{x} + \frac{f_{x}X}{Z}$$

$$v = c_{y} + \frac{f_{y}Y}{Z}$$

 

project2Dto3D

inline Eigen::Vector3d project2Dto3D(int x, int y, int d, float fx, float fy, float cx, float cy, float scale)
{
  float zz = float ( d ) /scale;
  float xx = zz* ( x-cx ) /fx;
  float yy = zz* ( y-cy ) /fy;
  return Eigen::Vector3d(xx, yy, zz);
}

위 함수는 2D 픽셀 좌표를 3차원 점으로 projection하는 함수이다.

$$X = \frac{Z}{f_{x}}(u-c_{x})$$

$$Y = \frac{Z}{f_{y}}(v-c_{y})$$

 

computeError

virtual void computeError() {
  const VertexSE3Expmap* v = static_cast<const VertexSE3Expmap*>(_vertices[0]);
  Eigen::Vector3d x_local = v->estimate().map(x_world_);
  float x = x_local[0] * fx_/x_local[2] + cx_;
  float y = x_local[1] * fy_/x_local[2] + cy_;

  // check x,y is in the border of the image
  if(x-4 < 0 || (x+4) >image_->cols || (y-4) <0 || (y+4) >image_->rows) {
    _error(0,0) = 0.0;
    this->setLevel(1);
  }
  else {
    _error(0,0) = getPixelValue(x,y) - _measurement;
  }
}

photometric error는 아래와 같이 정의한다.

\begin{equation}
\begin{aligned}
\mathbf{e}(\mathbf{T}) & =  \mathbf{I}_{1}(\mathbf{p}_{1})-\mathbf{I}_{2}(\mathbf{p}_{2}) \\
& = \mathbf{I}_{1} \bigg( \pi_{k}(\pi_{h}(\mathbf{X})) \bigg)-\mathbf{I}_{2}\bigg(  \pi_{k}(\pi_{h}(\mathbf{TX})) \bigg) \\
\end{aligned} 
\end{equation}

 

이 때 _measurement = $\mathbf{I}_{1}(\mathbf{p}_{1})$, getPixelValue(x,y) = $\mathbf{I}_{2}(\mathbf{p}_{2})$ 를 의미한다.

linearizeOplus

// plus in manifold
virtual void linearizeOplus()
{
  if(level() == 1) {
    _jacobianOplusXi = Eigen::Matrix<double, 1, 6>::Zero();
    return;
  }
  VertexSE3Expmap* vtx = static_cast<VertexSE3Expmap*>(_vertices[0]);
  Eigen::Vector3d xyz_trans = vtx->estimate().map(x_world_);   // q in book

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double invz = 1.0/xyz_trans[2];
  double invz_2 = invz*invz;

  float u = x*fx_*invz + cx_;
  float v = y*fy_*invz + cy_;

  // jacobian from se3 to u,v
  // NOTE that in g2o the Lie algebra is (\omega, \epsilon), where \omega is so(3) and \epsilon the translation
  Eigen::Matrix<double, 2, 6> jacobian_uv_ksai;

  jacobian_uv_ksai(0,0) = -x*y*invz_2 *fx_;
  jacobian_uv_ksai(0,1) = (1+(x*x*invz_2) ) *fx_;
  jacobian_uv_ksai(0,2) = -y*invz *fx_;
  jacobian_uv_ksai(0,3) = invz *fx_;
  jacobian_uv_ksai(0,4) = 0;
  jacobian_uv_ksai(0,5) = -x*invz_2 *fx_;

  jacobian_uv_ksai(1,0) = -(1+y*y*invz_2) *fy_;
  jacobian_uv_ksai(1,1) = x*y*invz_2 *fy_;
  jacobian_uv_ksai(1,2) = x*invz *fy_;
  jacobian_uv_ksai(1,3) = 0;
  jacobian_uv_ksai(1,4) = invz *fy_;
  jacobian_uv_ksai(1,5) = -y*invz_2 *fy_;

  Eigen::Matrix<double, 1, 2> jacobian_pixel_uv;

  jacobian_pixel_uv(0,0) = (getPixelValue(u+1,v) - getPixelValue(u-1,v)) / 2;
  jacobian_pixel_uv(0,1) = (getPixelValue(u,v+1) - getPixelValue(u,v-1)) / 2;

  _jacobianOplusXi = jacobian_pixel_uv * jacobian_uv_ksai;
}

위 코드는 Lie Theory를 사용하여 manifold 상에서 최적화를 수행할 때 사용하는 Jacobian을 정의한 코드이다. 이 때 이전에 설명한 Jacobian $\mathbf{J}  = \frac{\partial \mathbf{e}}{\partial \Delta \xi}  =  \frac{\partial \mathbf{I}}{\partial \mathbf{p}_{2}} \frac{\partial \mathbf{p}_{2}}{\partial \tilde{\mathbf{p}}_{2}} \frac{\partial \tilde{\mathbf{p}}_{2}}{\partial \mathbf{X}'} \frac{\partial \mathbf{X}'}{\partial \Delta \xi}$ 을 코드로 작성하는 작업이 필요하다. 자세한 항목은 아래와 같다.

\begin{equation}
  \begin{aligned}
\mathbf{J}  = \frac{\partial \mathbf{e}}{\partial \Delta \xi} & =  \frac{\partial \mathbf{I}}{\partial \mathbf{p}_{2}} \frac{\partial \mathbf{p}_{2}}{\partial \tilde{\mathbf{p}}_{2}} \frac{\partial \tilde{\mathbf{p}}_{2}}{\partial \mathbf{X}'} \frac{\partial \mathbf{X}'}{\partial \Delta \xi}  \\
    & = \begin{bmatrix} \nabla \mathbf{I}_{u} & \nabla \mathbf{I}_{v} \end{bmatrix}  \begin{bmatrix} -\frac{fX'Y'}{Z'^{2}} & \frac{f(1 + X'^{2})}{Z'^{2}} & -\frac{fY'}{Z'} & \frac{f}{Z'} & 0 & -\frac{fX'}{Z'^{2}} \\
      -\frac{f(1+Y'^{2})}{Z'^{2}} & \frac{fX'Y'}{Z'^{2}} & \frac{fX'}{Z'} & 0 & \frac{f}{Z'} & -\frac{fY'}{Z'^{2}} \end{bmatrix} \in \mathbb{R}^{1 \times 6}
  \end{aligned} 
\end{equation}

 

References

1. [blog] Introduction to Motion Estimation with Optical Flow 

2. [blog] Optical flow 루카스-카나데 방법 - 임이지님 블로그 

3. [youtube] SLAMKR Study Season1 - Optical Flow 

4. [post] 입문 Visual SLAM 책 - SLAMKR