본 포스트는 Claus Brenner의 SLAM 강의 중 Chapter E: Particle Filter 부분을 정리한 자료이다. Claus Brenner의 SLAM 강의는 [1]에서 볼 수 있다.
Particle filter를 이해하는데 필요한 기반 지식은 확률 이론(Probability Theory) 개념 정리 포스팅을 참조하면 된다.
Kalman filter (KF, EKF, ESKF, IEKF)에 대해 알고 싶으면 칼만 필터(Kalman Filter) 개념 정리 포스트를 참조하면 된다.
Introduction
본 포스트에서는 Robot Localization에 사용하는 파티클 필터에 대한 내용을 다룬다. 따라서 맵의 크기와 Landmark의 좌표는 모두 알고 있다고 가정한다. 또한 Landmark는 모두 동일한 크기의 실린더이다.
Claus Brenner의 SLAM 강의 중 Recursive Bayesian Filter에 대한 내용은 Chapter C에서 다루므로 여기서는 다루지 않는다. Particle Filter SLAM (aka FastSLAM)에 대한 내용은 Chapter G에서 다루므로 여기서는 다루지 않는다.
Probability Distribution and Particle Sampling
확률분포와 파티클 사이의 변환은 여러 가정 하에 다음과 같이 수행할 수 있다. 우선 주어진 확률분포로부터 파티클은 다음과 같이 샘플링할 수 있다.

반대로 주어진 파티클로부터 확률분포는 다음과 같이 추정할 수 있다.

Freiburg 대학의 SLAM 강의 중 Particle Filter 강의를 보면 해당 샘플링에 대한 내용이 자세하게 나와 있다. 자세한 내용은 [2] 참조하면 된다.
Particle Filter
파티클 필터는 Recursive Bayesian Filter에서 $\text{bel}(x_{t})$를 랜덤하게 샘플링한 파티클들의 집합 $\{x_{t}^{[i]}\}$로 표현하는 방법을 말한다. 파티클 필터는 다음과 같은 특징을 가지고 있다.
- Non-parametric 방법 중 하나이다. ($\mu, \sigma$와 같은 파라미터를 찾지 않아도 된다)
- 실제 로봇의 정확한 위치를 찾는 것이 아닌 대략적인 위치를 근사하는(approximate) 방법 중 하나이다

- Multimodal distribution을 표현할 수 있다.

Motivation of Particle Filter
파티클 필터는 SLAM Initialization 과정에서 초기 포즈 설정이 어려운 문제를 어느 정도 해결할 수 있다. 각 그림의 의미는 다음과 같다.

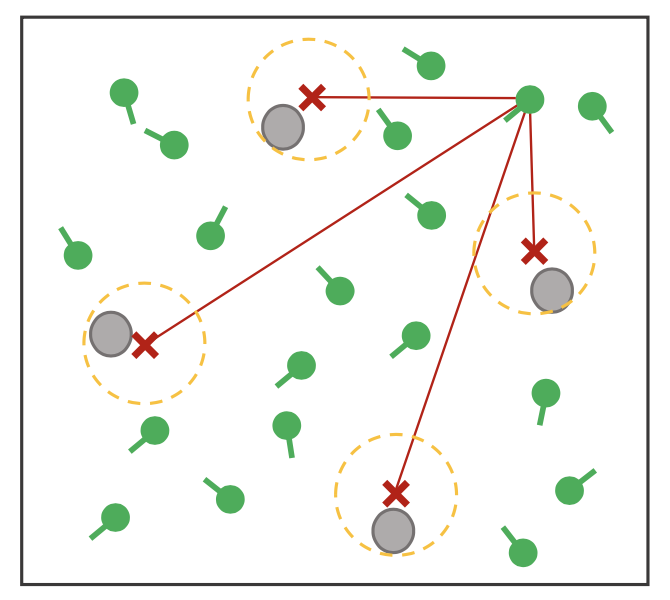
만약, 다음과 같이 Robot의 초기 포즈를 아는 경우, Landmark measurement를 통해 Localization을 수행할 수 있다.
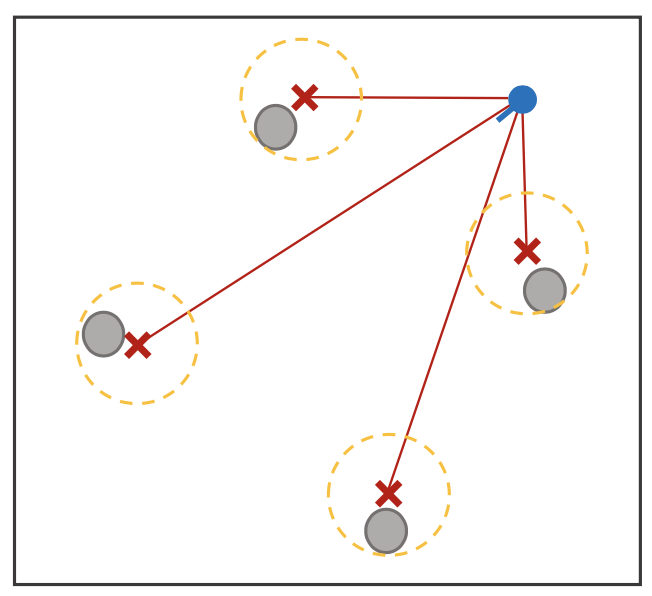
하지만, 아래와 같이 로봇의 초기 포즈를 모르는 경우 로봇이 랜덤한 곳에 위치하게 되고 잘못된 Landmark correspondence를 통해 Locailzation이 실패할 가능성이 매우 높아지게 된다.
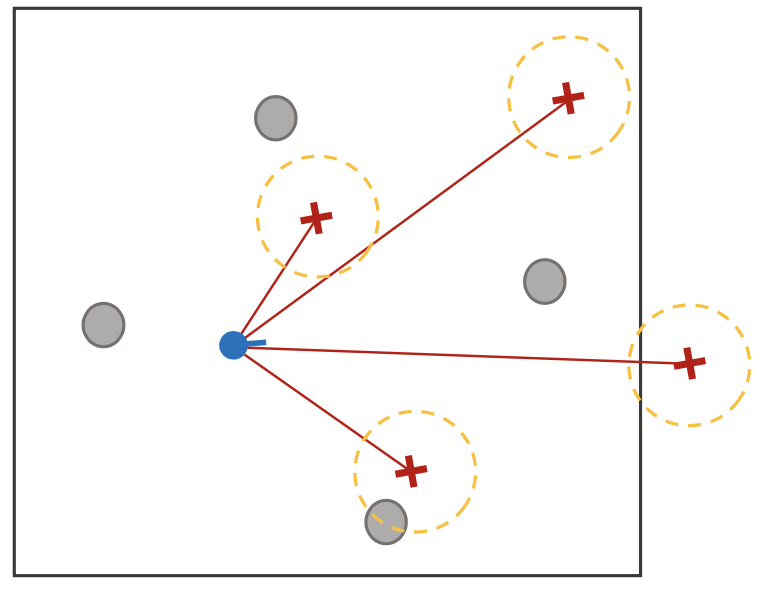
따라서 로봇의 초기 위치를 랜덤하게 여러 위치에 산개시켜 놓은 다음 가장 Landmark correspondence가 가장 높은 지점의 위치를 초기 포즈로 설정하는 방법이 효율적이다.
Prediction Step
$t$ 스텝에서 파티클들은 $x_{t} = \{ x_{t}^{[1]}, x_{t}^{[2]}, \cdots, x_{t}^{[M]} \}$과 같이 정의할 수 있고 이 때, predicted particle $\bar{x}_{t}^{[m]}$은 다음과 같이 정의할 수 있다.
\begin{equation} \boxed{ \begin{aligned} & \text{for } m=1 \text{ to } M: \\ & \quad \quad \text{sample } \bar{x}_{t}^{[m]} \simeq p(x_{t} | x_{t-1}^{[m]}, u_{t}) \end{aligned} } \end{equation}
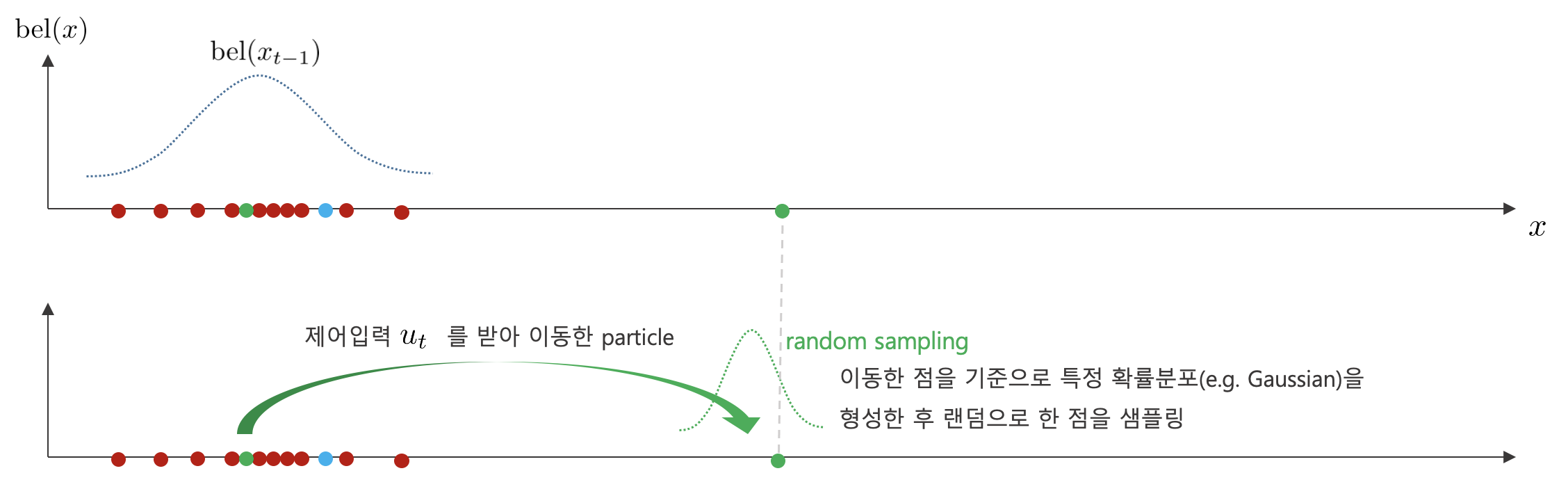
위 식은 $t-1$ 스텝에서 m번째 파티클이 제어 입력 $u_{t}$를 받아 이동한 후 이동한 점을 기준으로 특정 확률 분포를 형성하는데 해당 확률분포에서 랜덤으로 하나를 샘플링한 파티클을 predicted particle $\bar{x}_{t}^{[m]}$로 정의한다.
1D Example
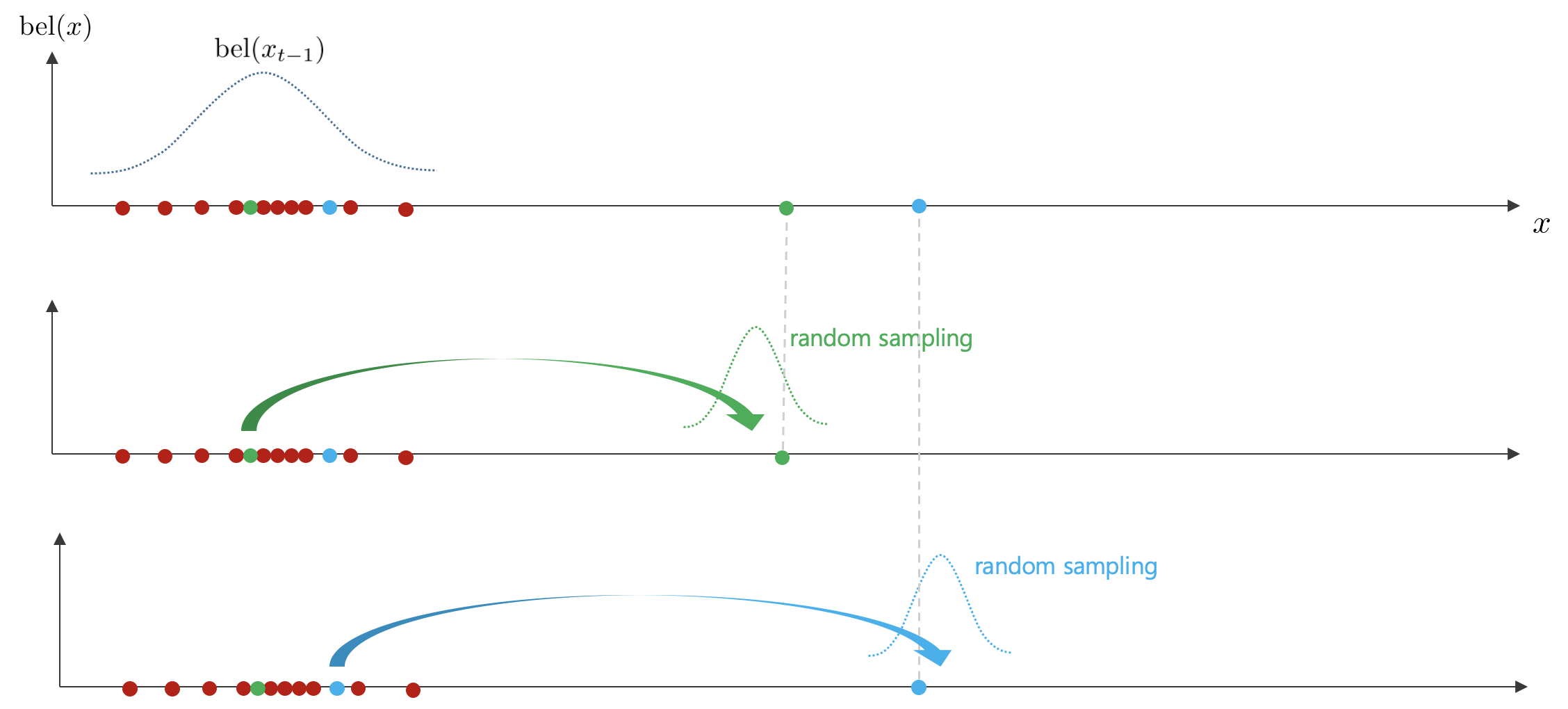
Prediction Step을 1D 직선 상에서 설명하면 다음과 같다.
1. $t-1$ 스텝에서 다음과 같이 파티클들이 분포해 있다고 가정하자.

2. $t-1$ 스텝에서 제어 입력 $u_{t}$를 받아 다음과 같이 한 점이 이동한다. 그리고 이동한 점을 기준으로 가우시안 분포를 형성한 후 랜덤 샘플링을 수행한다.
3. 이러한 과정을 다른 점에 대해서도 수행한다.
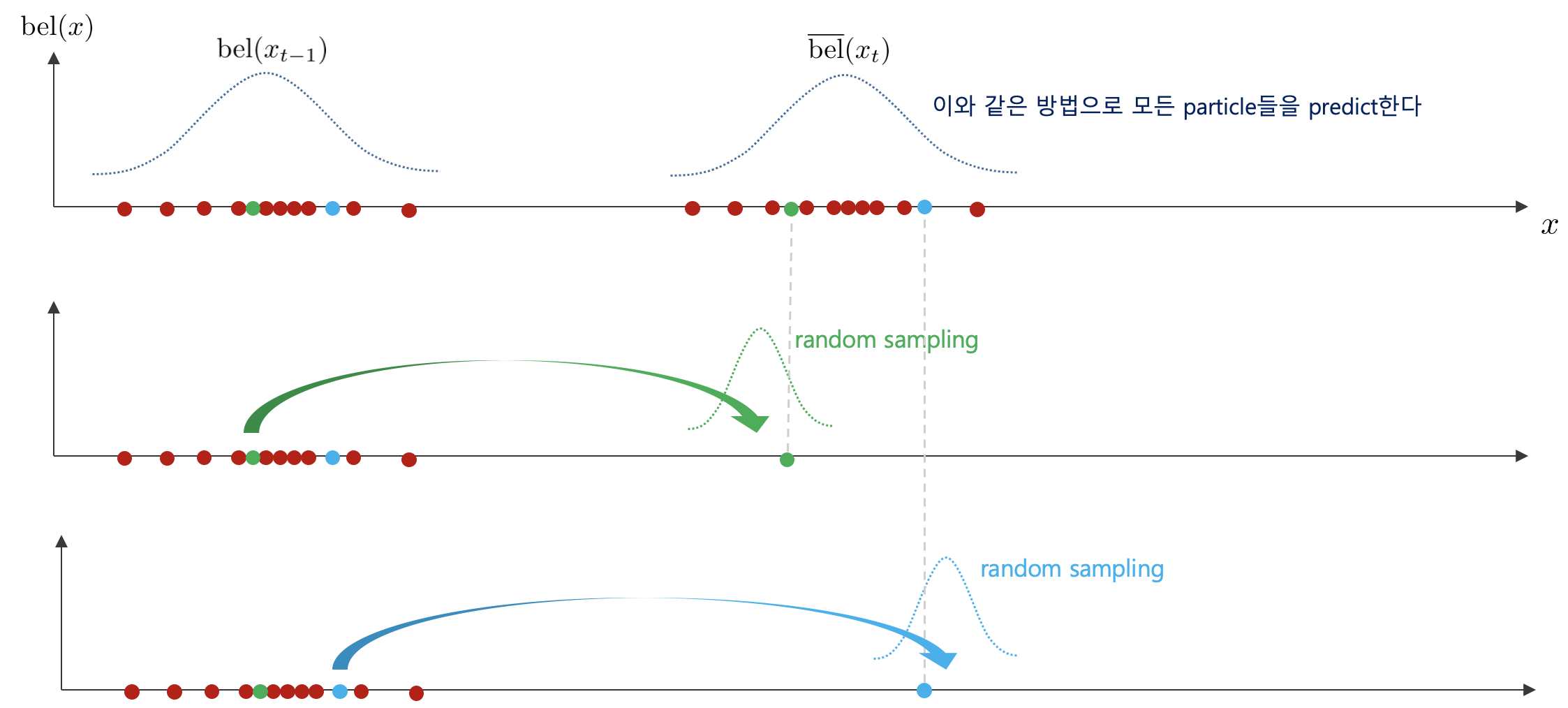
4. 이와 같은 방법으로 모든 파티클들을 예측하여 predicted paritcle $\bar{x}_{t}^{[m]}$를 생성한다.
2D Example
2D 평면에서 로봇의 이동으로 prediction step을 표현하면 다음과 같다.

1. 다음과 같이 $t-1$ 스텝에서 로봇의 위치를 추정하고 있을 때 제어 입력 $u_{t}$가 들어온다고 가정하자. 특정 한 점이 제어 입력 $u_{t}$만큼 이동한 후 가우시안 분포를 생성하여 한 점을 다시 랜덤 샘플링한다.
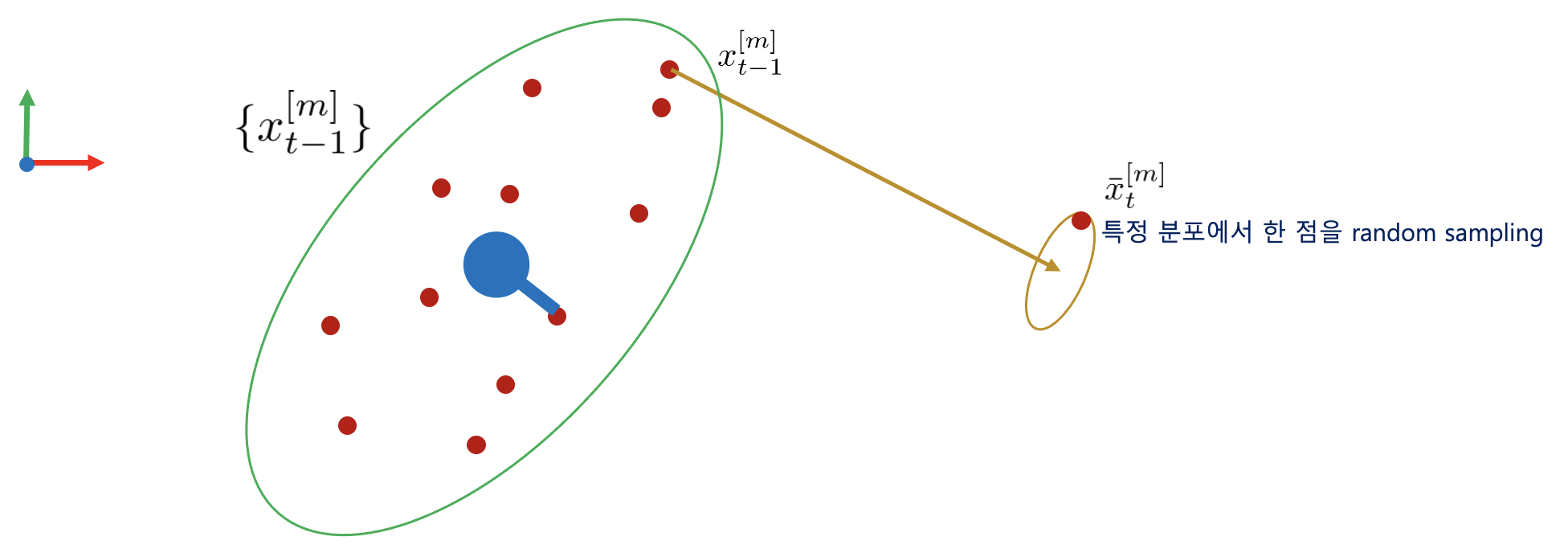
2. 이를 모든 점에 대해 수행하면 새로운 predicted particle set을 구할 수 있다.
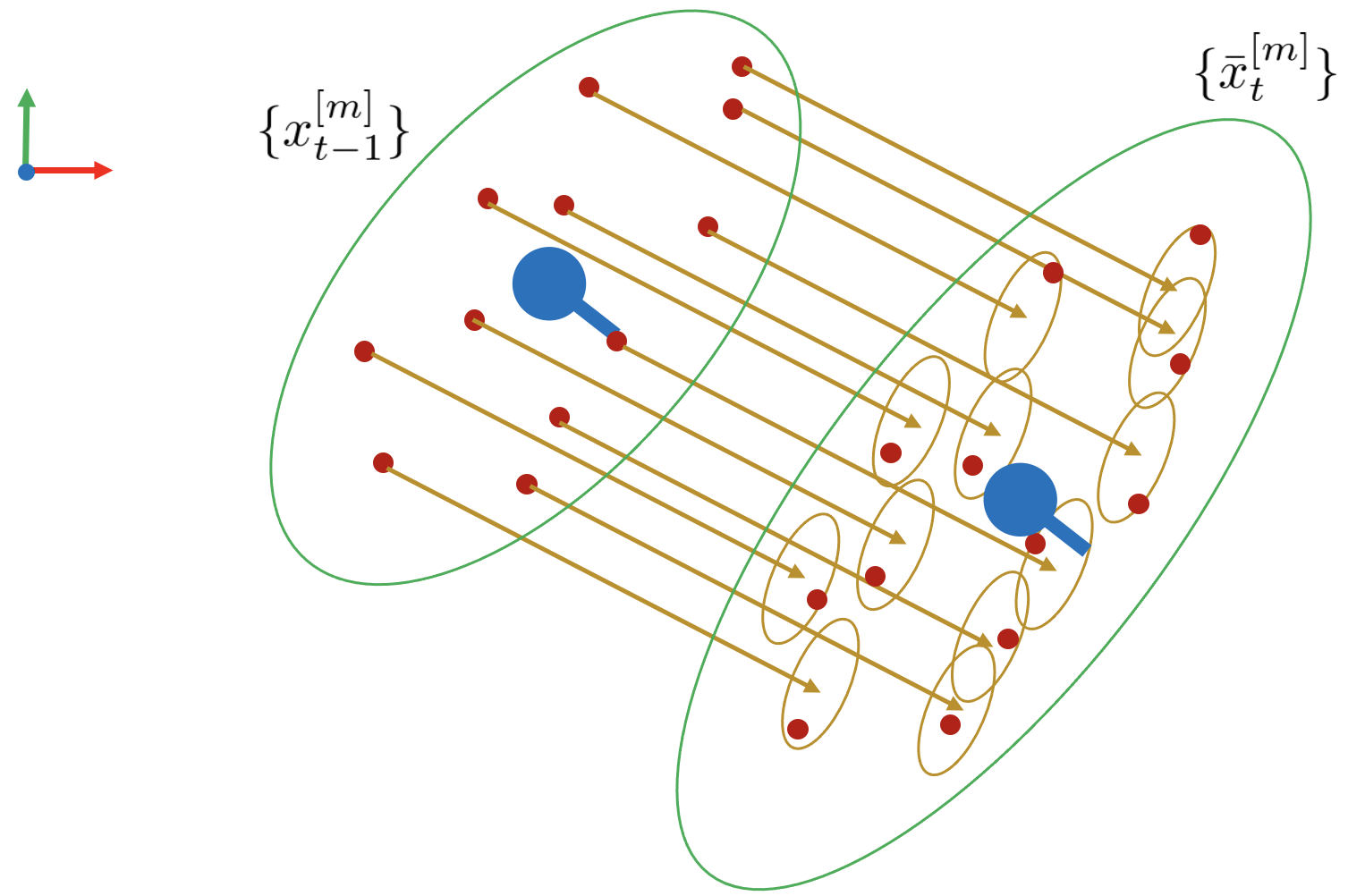
Control Input
제어 입력(control input)을 받은 로봇의 predicted state는 다음과 같이 수식으로 표현할 수 있다.
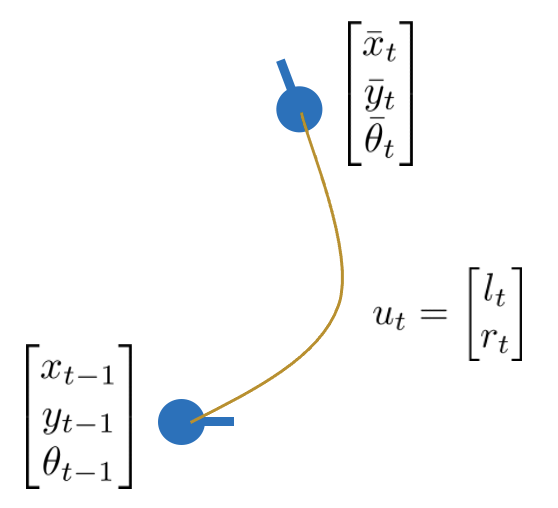
\begin{equation} \begin{aligned} \bar{\mathbf{x}}_{t}^{[m]} = g(\mathbf{x}_{t-1}^{[m]},\begin{bmatrix} l_{t} \\ r_{t} \end{bmatrix} ) \end{aligned} \end{equation}
위 수식은 exact formula이지만 실제 로봇의 경우 제어 입력에도 노이즈가 포함되어 있으므로 제어 입력도 확률변수로 변경한다.
\begin{equation} \begin{aligned} \begin{bmatrix} l_{t} \\ r_{t} \end{bmatrix} \rightarrow \begin{bmatrix} l'_{t} \\ r'_{t} \end{bmatrix} \end{aligned} \end{equation}
노이즈가 있는 제어 입력은 다음과 같이 정규분포로 가정하고 하나의 값을 샘플링해서 사용한다.
\begin{equation} \begin{aligned} & \text{sample } l'_{t} \simeq \mathcal{N}(l_{t}, \sigma^{2}_{l_{t}}) \\ & \text{sample } r'_{t} \simeq \mathcal{N}(r_{t}, \sigma^{2}_{r_{t}}) \end{aligned} \end{equation}
- $\sigma^{2}_{l_{t}} = (\alpha_{1} \cdot l)^{2} + (\alpha_{2} \cdot (l - r))^{2}$
- $\sigma^{2}_{r_{t}} = (\alpha_{1} \cdot r)^{2} + (\alpha_{2} \cdot (l - r))^{2}$
최종적으로 $t$번째 predicted state는 다음과 같이 나타낼 수 있다.
\begin{equation} \begin{aligned} \bar{\mathbf{x}}_{t}^{[m]} = g(\mathbf{x}_{t-1}^{[m]},\begin{bmatrix} l'_{t} \\ r'_{t} \end{bmatrix} ) \end{aligned} \end{equation}
Correction Step
파티클 필터의 Correction Step은 다음과 같다.
\begin{equation} \boxed{ \begin{aligned} & x_{t} = \{\} \ \text{ empty set} \\ & \text{for } m = 1 \text{ to } M: \\ & \quad \quad w_{t}^{[m]} = p(z_{t} | x_{t}^{[m]} ) \\ & \quad \quad \text{resample } \bar{x}_{t}^{[m]} \text{ with probability } \propto w_{t}^{[m]} \\ & \quad \quad x_{t} = x_{t} \cup \{ \bar{x}_{t}^{[m]} \} \end{aligned} } \end{equation}
- $w_{t}^{[m]} = p(z_{t} | x_{t}^{[m]} )$ : 해당 항을 Importance factor라고 한다
- $\text{resample } \bar{x}_{t}^{[m]} \text{ with probability } \propto w_{t}^{[m]}$ : 해당 항을 Importance sampling이라고 한다
Importance factor
다음과 같이 로봇이 주어졌다고 가정하자
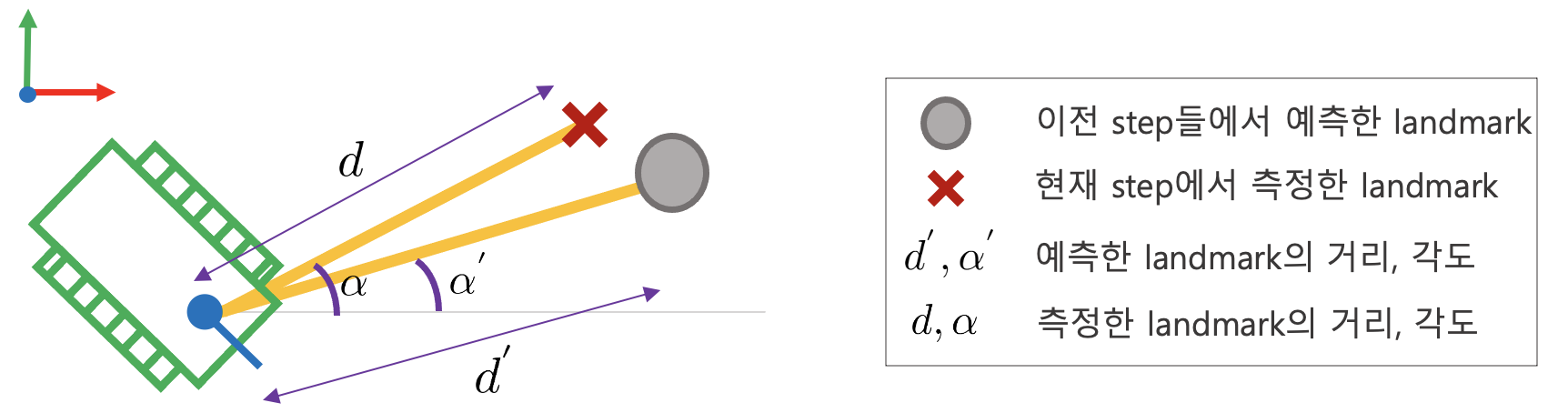
이 때, weight $w$의 크기는 다음과 같이 계산할 수 있다.
\begin{equation} \begin{aligned} p(z|x) & = p(d-d') \cdot p(\alpha - \alpha') \\ & = \mathcal{N}(d-d';0,\sigma^{2}_{d}) \cdot \mathcal{N}(\alpha-\alpha' ; 0, \sigma^{2}_{\alpha}) \end{aligned} \end{equation}
각각 Landmark에 대한 $p(z_{i} | x)$를 구한 다음 모두 곱해주는 방식을 통해 weight $w$의 크기를 계산할 수 있다.
\begin{equation} \begin{aligned} \therefore w = p(z|x) = \Pi_{i} p(z_{i} | x) \end{aligned} \end{equation}
Importance Sampling (or Resampling)
다음으로 리샘플링 과정은 다음과 같다.
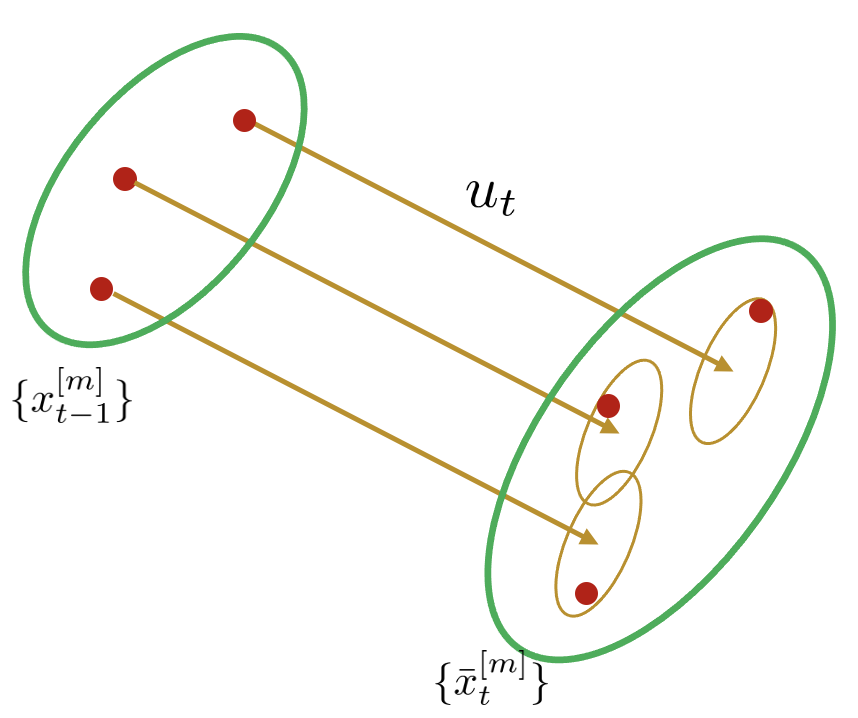
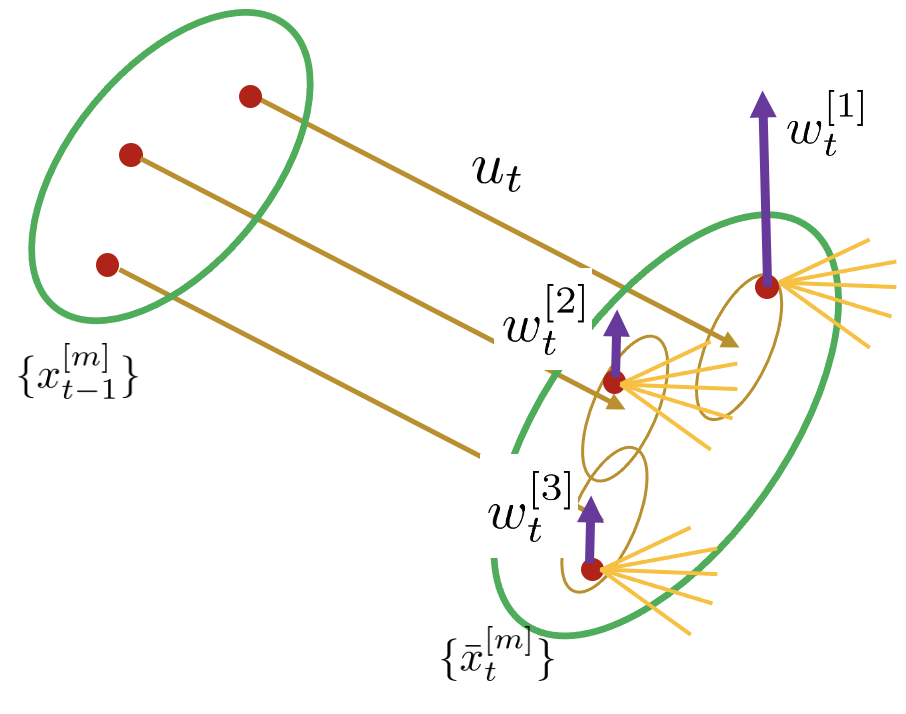
1. 아래 그림과 같이 제어 입력 $u_{t}$에 대한 predicted particle을 샘플링한다
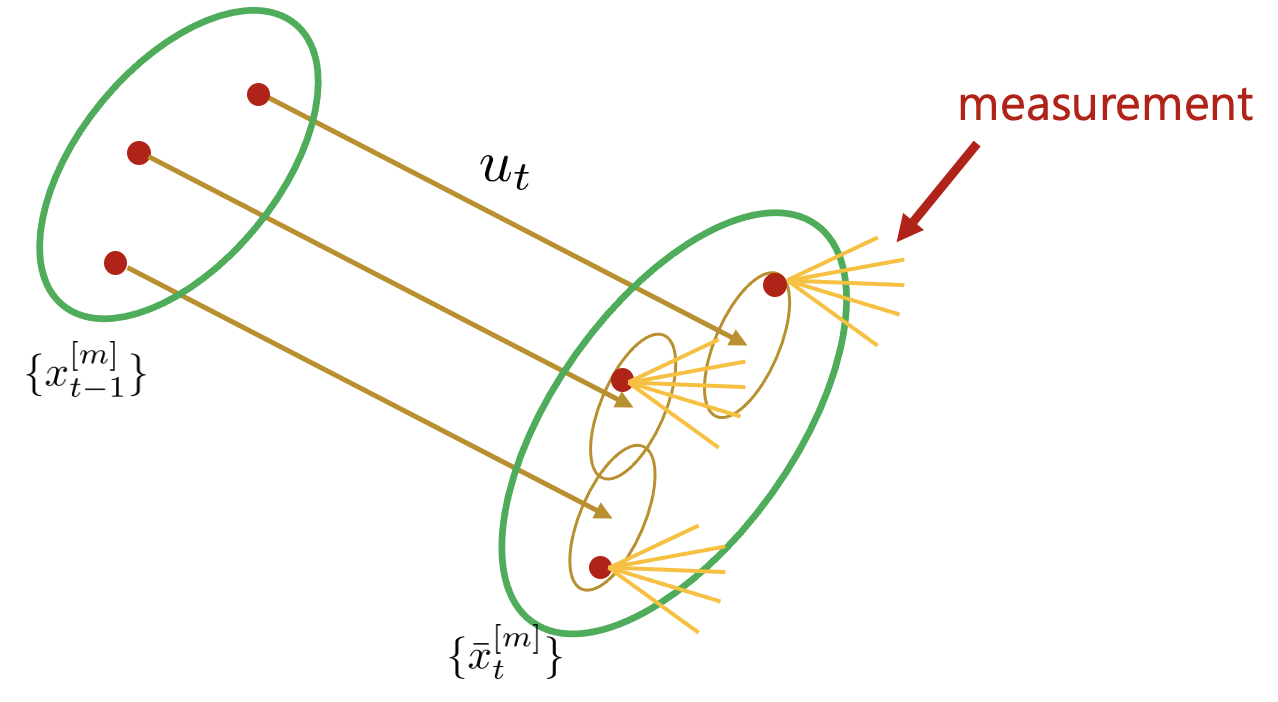
2. 샘플링한 각각의 파티클에 대하여 measurement를 수행한다
3. 해당 measurement correspondence가 높은 정도에 따라 각 파티클에 weight를 부여한다
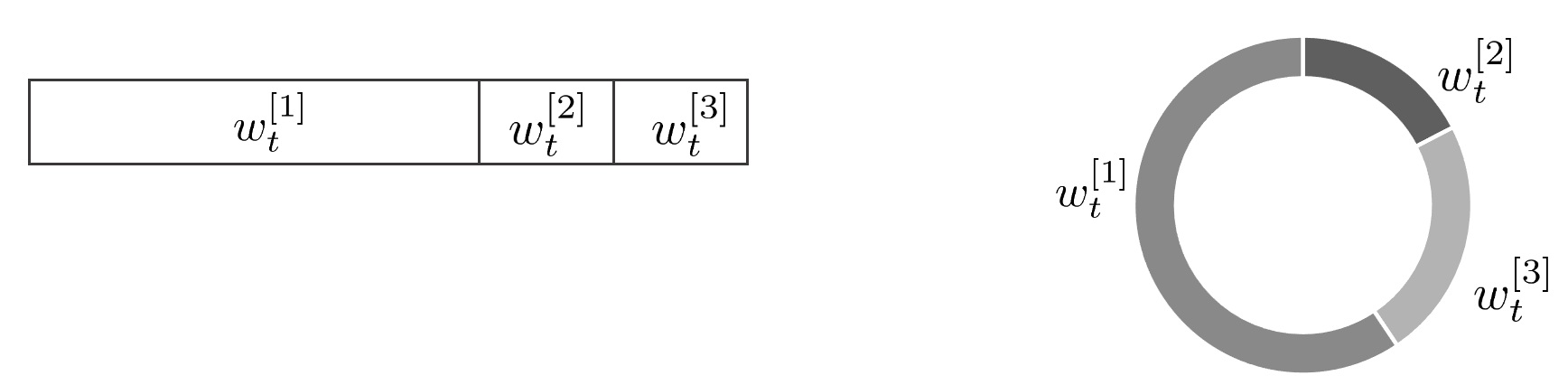
4. weight를 아래와 같이 크기별로 정렬하고 정렬된 bar 또는 roulette에서 다시 샘플링을 수행한다. 해당 과정을 리샘플링이라고 한다.
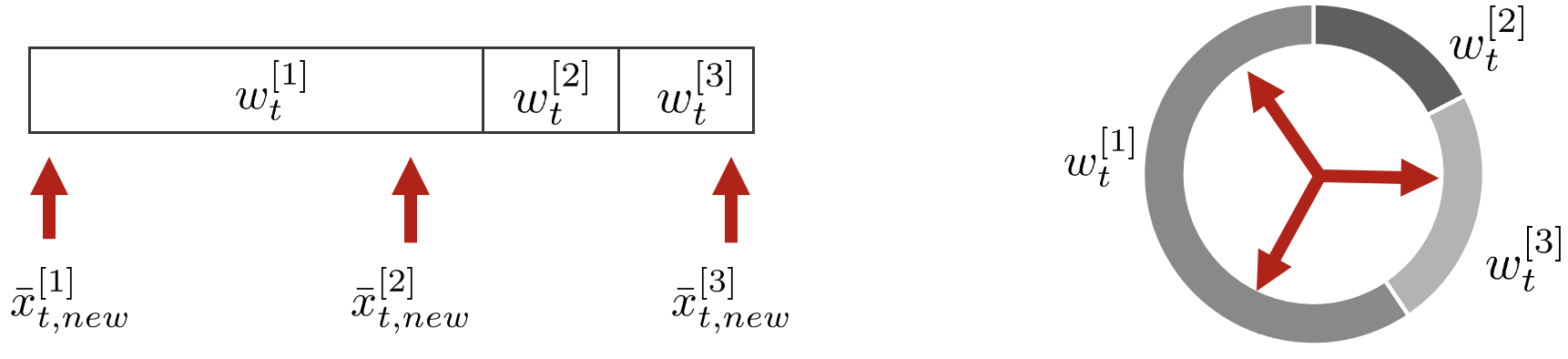
5. 이 때, 기존 파티클의 개수만큼 일정 간격을 두고 샘플링을 수행하면 자연스럽게 weight가 큰 파티클들이 많이 선택된다.
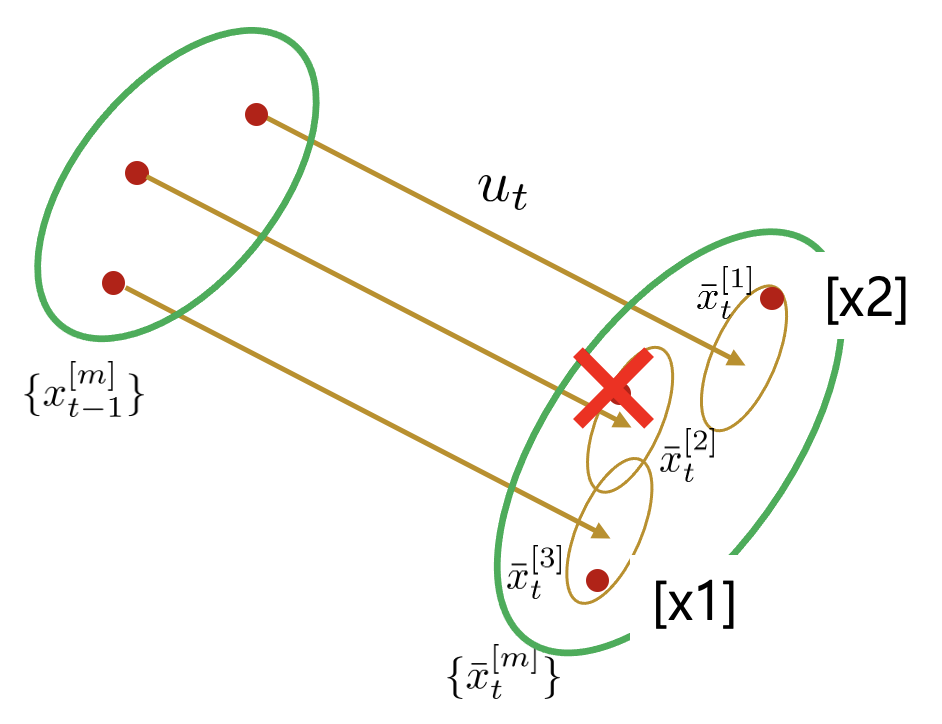
6. 최종적으로 $\bar{x}_{t}^{[1]}$ 위치에 중복된 점 2개, $\bar{x}_{t}^{[3]}$ 위치에 점 1개가 리샘플링된다.
Density Estimation
본 섹션에서는 파티클들의 분포를 통해 실제 로봇의 위치를 판단하는 여러 방법에 대해 설명한다. 다음과 같이 파티클들이 분포하고 있을 때 실제 로봇의 위치는 어디에 있다고 판단하는 게 가장 적절할까?

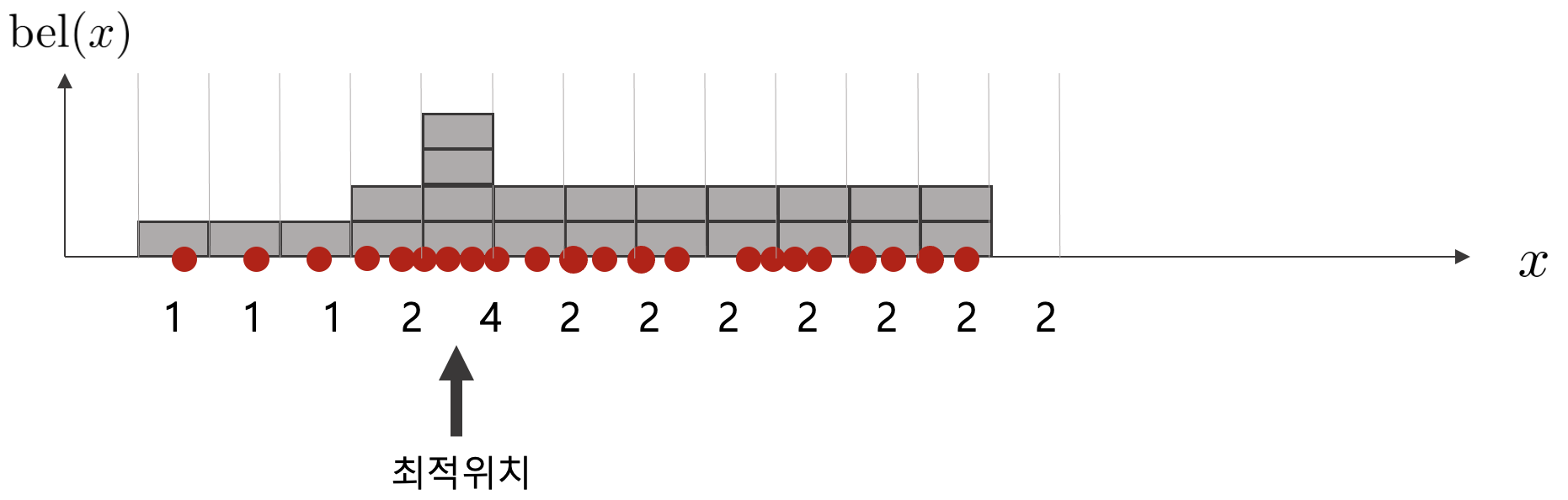
Histogram over state space
histogram bin에 포함되는 파티클들의 개수에 따라 최적 위치를 선택하는 방법
Kernel Density
각각 파티클마다 특정 분포 (e.g., 가우시안)을 갖는다고 가정한 후 모든 분포의 합을 더하여 로봇의 위치를 구하는 방법

K-means clustering
파티클들을 k개의 클러스터로 분리한 후 각각의 평균을 취해서 로봇의 위치를 구하는 방법

Normal Distribution
해당 파티클들이 정규분포를 가진다고 가정한 후 평균과 분산을 구하고 이를 통해 로봇의 위치를 구하는 방법. Unimodal인 경우에만 사용 가능하다. 본 SLAM 강의에서는 해당 방법을 통해 로봇의 위치를 계산했다.

2D 평면의 경우 로봇의 위치는 다음과 같이 추정할 수 있다.
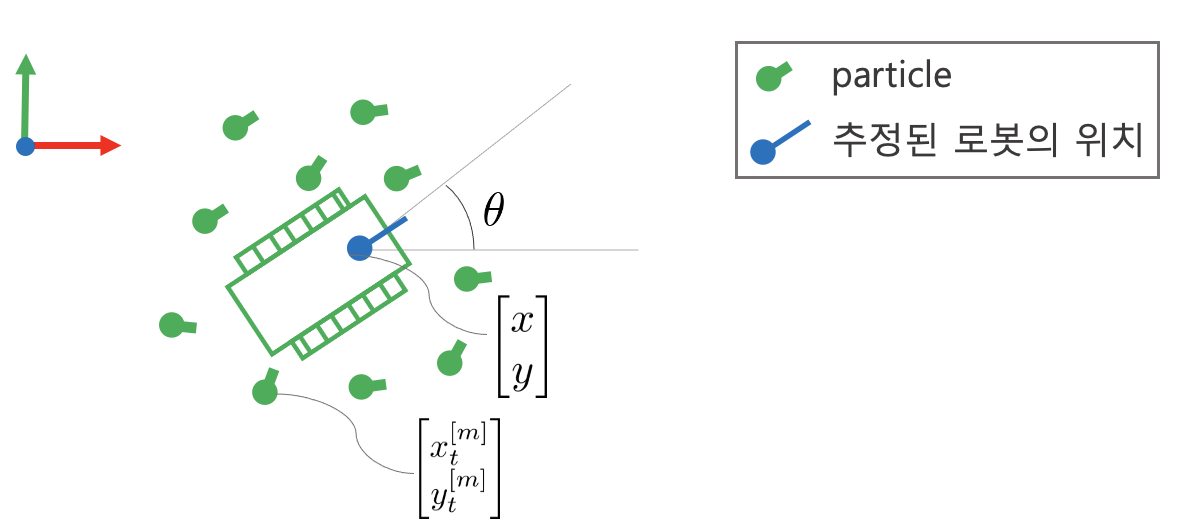
위치는 $\begin{bmatrix} x\\ y\end{bmatrix}=\frac{1}{M}\sum_{m}\begin{bmatrix}x_{t}^{[m]}\\ y_{t}^{[m]}\end{bmatrix}$와 같이 파티클 분포의 평균으로 구할 수 있다. 하지만 헤딩 각도의 경우 modulo에 신경을 써야 한다.
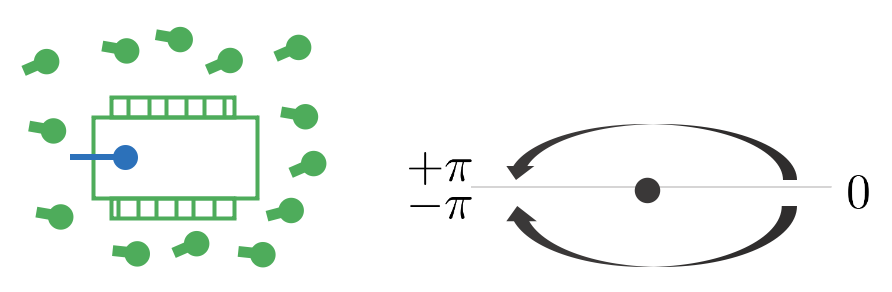
만약 위와 같이 파티클들이 분포하고 있는 경우 헤딩 각도를 표시할 때 어떤 파티클은 $\epsilon + \pi$이고 어떤 파티클은 $\epsilon - \pi$가 되어 합을 취하면 0이 되는 현상이 발생한다. 따라서 헤딩 각도의 경우 벡터를 사용하여 해당 문제를 해결한다.
\begin{equation} \begin{aligned} & v_{x} = \frac{1}{M}\sum \cos\theta_{i} \\ & v_{y} = \frac{1}{M}\sum \sin\theta_{i} \\ & \hat{\theta} = \text{atan}(\frac{v_{x}}{v_{y}}) \end{aligned} \end{equation}
Resampling Strategy
로봇이 움직이지 않는 경우 스텝이 지날수록 파티클들이 하나의 점으로 리샘플링되는 현상이 발생한다.
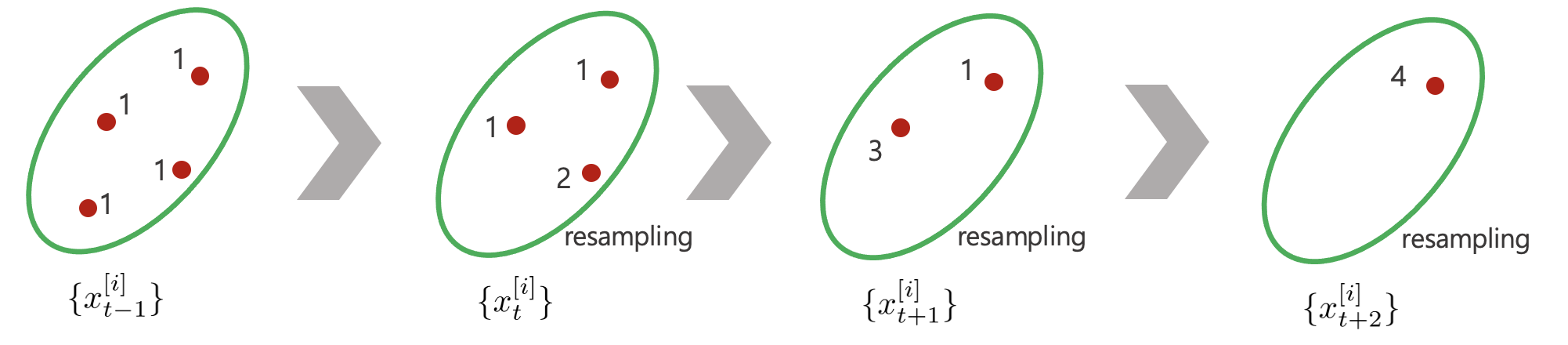
위와 같이 리샘플링을 너무 자주하는 경우 로봇이 다시 이동할 때 파티클 분포의 다양성이 감소할 수 있다. 반대로 리샘플링을 너무 가끔하는 경우 파티클들의 분포가 넒게 퍼지게 된다. 따라서 다음과 같은 방법을 통해 리샘플링을 적절하게 수행한다.
1. 로봇이 정지하고 있을 때는 리샘플링을 수행하지 않는다.
2. 현재 스텝의 weight들이 이전 스텝들의 영향을 받도록 설정한다.
\begin{equation} \begin{aligned} w_{t}^{[i]}=\begin{cases} 1.0 & \text{ if resampling took place} \\ p(z_{t}|x_{t}^{[m]}) \cdot w_{t-1}^{[m]} & \text{ if no resampling took place} \end{cases} \end{aligned} \end{equation}
3. weight의 분산을 사용하여 해당 상황에서 리샘플링이 필요한지 아닌지 결정한다.
Particle Deprivation
다음과 같이 true state의 파티클들이 리샘플링으로 전부 사라질(wipe out) 가능성이 존재한다.
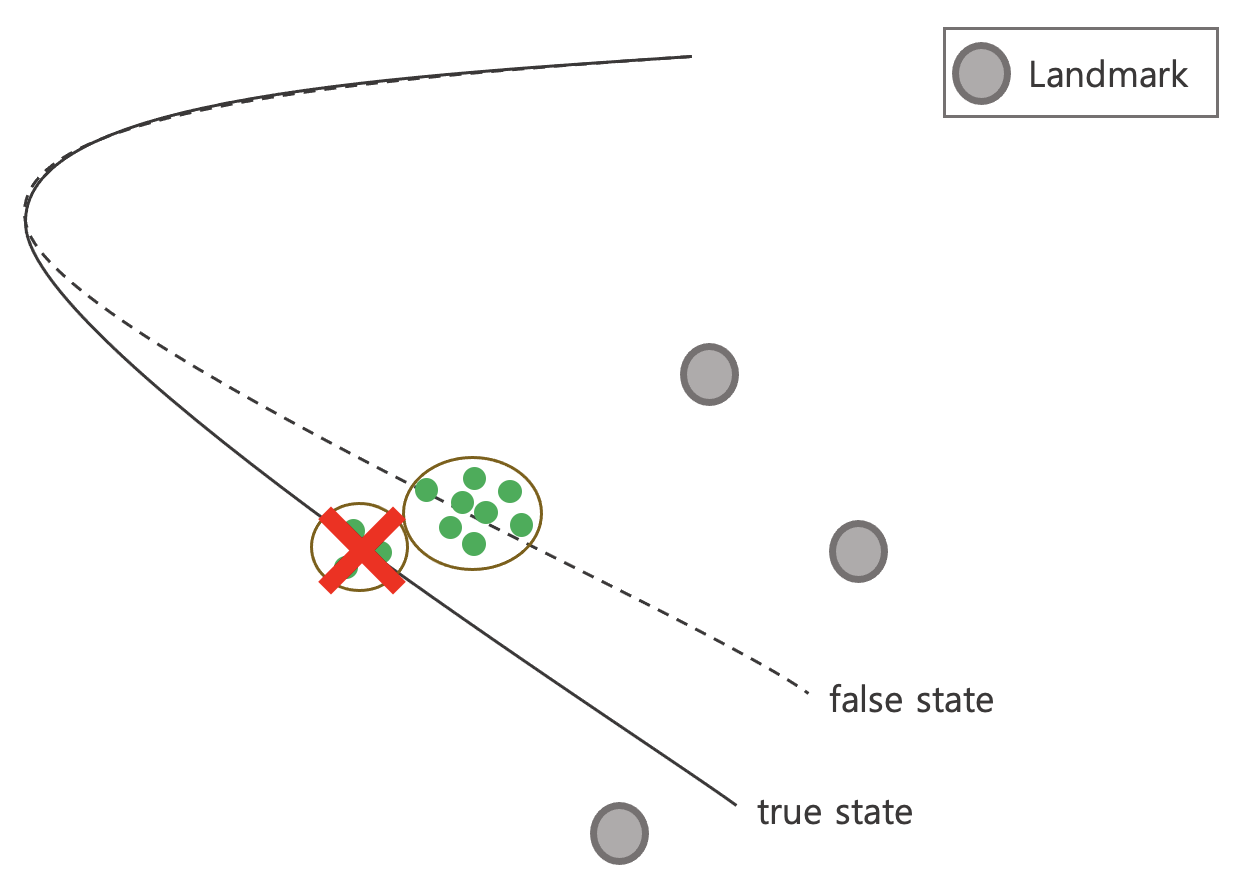
이는 보통 파티클의 개수 M이 너무 작을 때 자주 발생한다. 가장 유명한 솔루션은 리샘플링 이후 랜덤하게 파티클들을 추가적으로 샘플링하는 방법이다. 해당 방법은 true state를 놓지는 현상을 해결할 수 있으나 posterior의 정확도가 떨어진다는 단점이 존재한다.
References
[1] https://www.youtube.com/watch?v=B2qzYCeT9oQ...
[2] http://jinyongjeong.github.io/2017/02/22/lec11_Particle_filter/
Closure
pdf 버전은 아래 링크에서 다운로드받을 수 있다
'Fundamental' 카테고리의 다른 글
| [SLAM] 에러와 자코비안 정리(Errors and Jacobians) 정리 Part 1 (15) | 2023.01.08 |
|---|---|
| Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 3 (6) | 2022.10.10 |
| Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 2 (5) | 2022.08.31 |
| Quaternion kinematics for the error-state Kalman filter 내용 정리 Part 1 (4) | 2022.08.27 |
| 칼만 필터(Kalman Filter) 개념 정리 (+ KF, EKF, ESKF, IEKF, IESKF) (6) | 2022.06.18 |
 A L I D A
A L I D A





